Chapter 5 The Performance of Feedback Control Systems

Chapter 5 The Performance of Feedback Control Systems Test Input Signals Performance of a Second-Order System Effects of Third Pole and a Zero on the Second-Order System Response Estimation of the Damping Ratio The Steady-State Error of Feedback Control Systems Performance Indices

Preview • The ability to adjust the transient and steady-state response of a feedback control system is a beneficial outcome of the design of control systems. • Input signals such as step and ramp are used to test the response of the control system. • In this chapter, common time-domain specifications are introduced: – Transient Response and Steady-State Response – Percent overshoot – Settling time – Time to peak – Time to Rise – Steady-State Tracking Error. • The concept of a performance index that represents a system’s performance by a single number (or index) will be considered. .

Test Input Signals

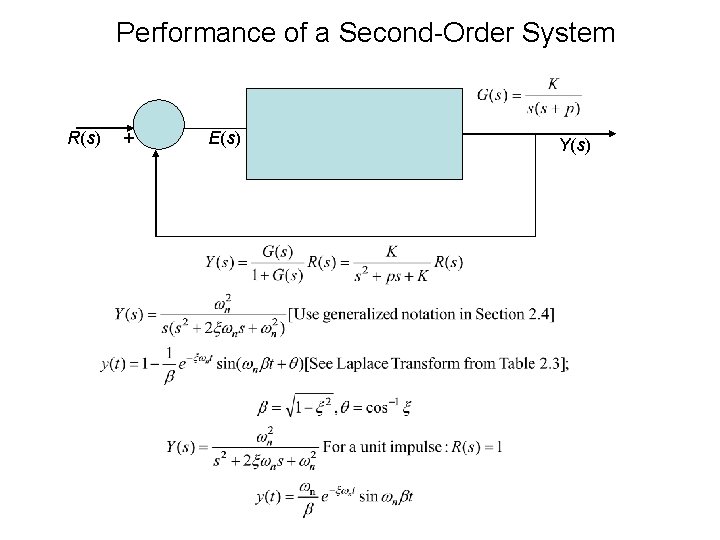
Performance of a Second-Order System R(s) + E(s) Y(s)

Standard Performance Measures

The Steady-State Error of Feedback Control Systems K 1 Ea(s) + G(s) - H(s) Y(s)

Performance Indices A performance index is a quantitative measure of the performance of a system and is chosen so that emphasis is given to the important system specifications. A system is considered an optimum control system when the system parameters are adjusted so that index reaches an extremum value, commonly a minimum value. A performance index, to be useful, must be a number that is always positive or zero

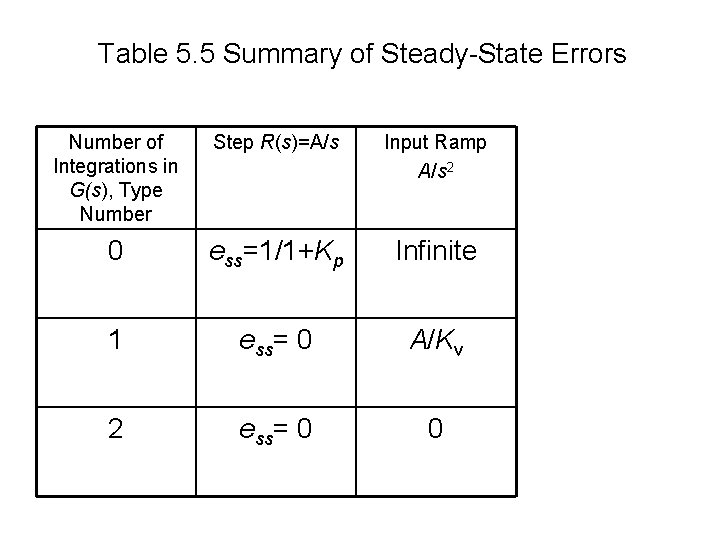
Table 5. 5 Summary of Steady-State Errors Number of Integrations in G(s), Type Number Step R(s)=A/s Input Ramp A/s 2 0 ess=1/1+Kp Infinite 1 ess= 0 A/Kv 2 ess= 0 0

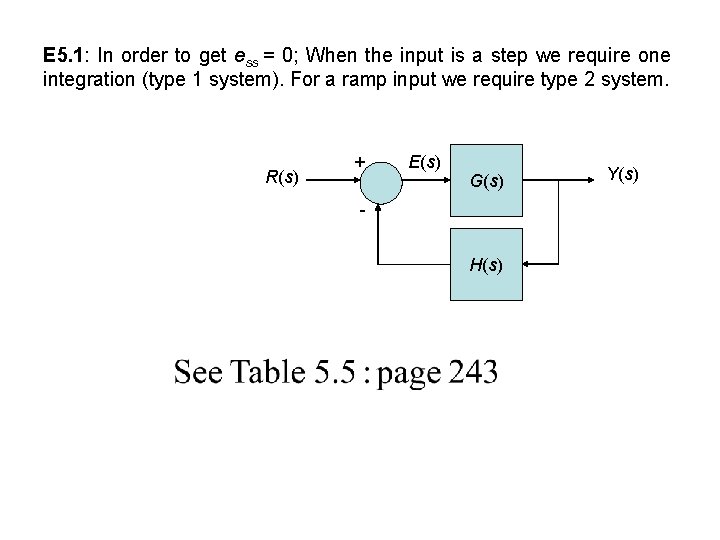
E 5. 1: In order to get ess = 0; When the input is a step we require one integration (type 1 system). For a ramp input we require type 2 system. R(s) + E(s) G(s) H(s) Y(s)

The Optimum Coefficients of T(s) Based on the ITAE Criterion for a Step Input

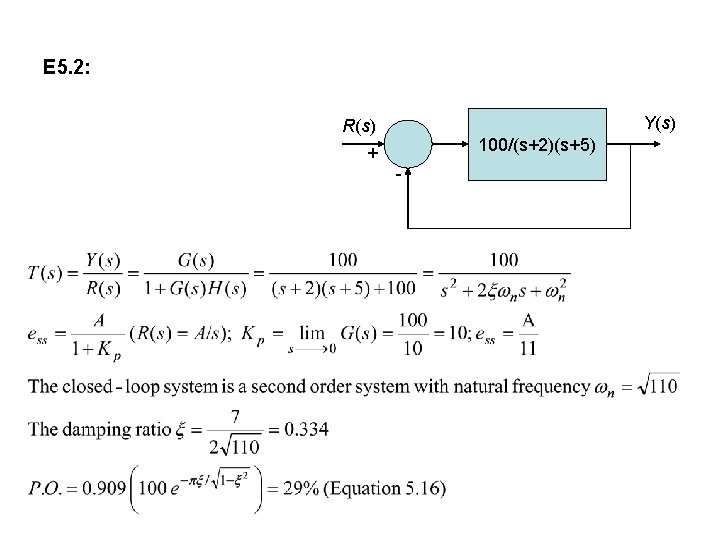
E 5. 2: Y(s) R(s) 100/(s+2)(s+5) + -

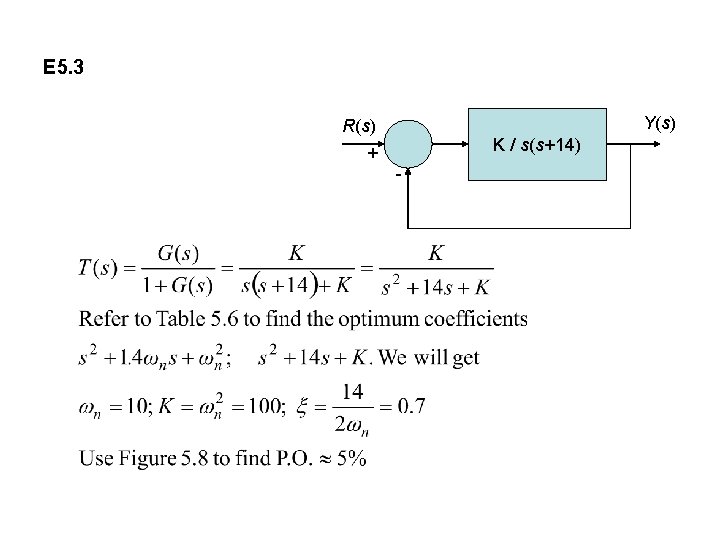
E 5. 3 Y(s) R(s) K / s(s+14) + -

E 5. 8:

E 5. 10 The system is a type 1 (Table 5. 5). The error constants are R(s) + E(s) G(s) H(s) Y(s)

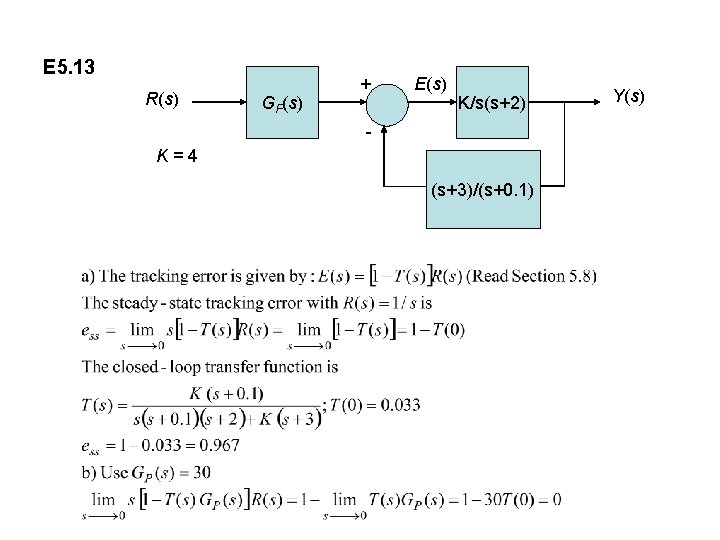
E 5. 13 R(s) GP(s) + E(s) K/s(s+2) K=4 (s+3)/(s+0. 1) Y(s)