CHAPTER 5 The Energy Storage Elements The capacitor

The capacitor is a device that stores charge The charge and the applied voltage

Capacitor Energy The instantaneous power delivered to the capacitor is: The energy stored in

Example 5. 1 A voltage source is applied to a 5 -F capacitor as

Example 5. 2 A current source is applied to a 5 -F capacitor. Sketch

The capacitor voltage is related to area Under current source. For example area at

5. 1. 1 Capacitors in Parallel The terminal voltage is equal to the voltage

Capacitors in Series 5. 1. 1 v(t) = v 1(t) + v 2(t) +

The Inductor A device that stores energy in its magnetic field The current produces

The relation between the voltage and current of inductor is This relation can be

The energy stored in an inductor The instantaneous power of an inductor Thus the

Example 5. 3 A current source is applied to a 5 -H inductor as

Example 5. 4 A voltage source is applied to a 5 -H inductor as

v(t)=2 t V(t)= -2 t+4 0<t<1 1<t<2 i. L=t 2/2 i. L= -t 2/2+2

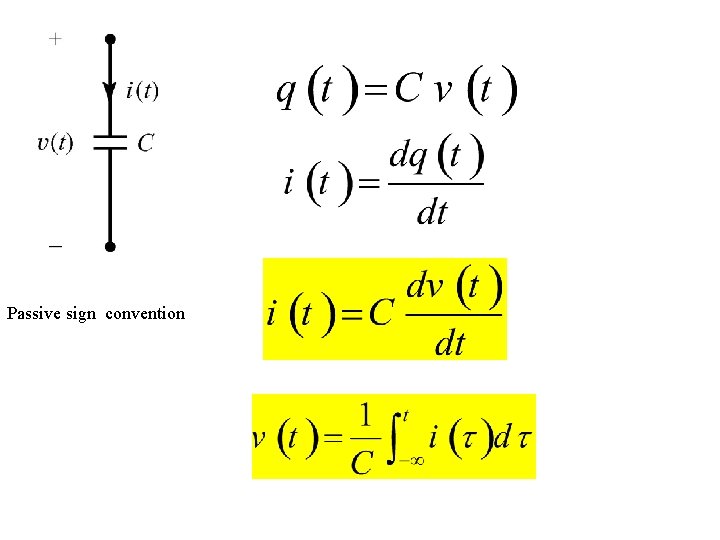
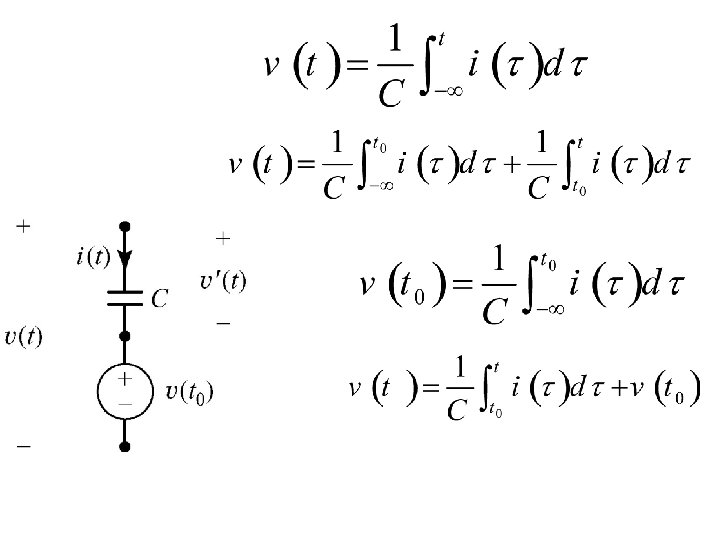
Slides: 25

Download presentation

CHAPTER 5 The Energy Storage Elements

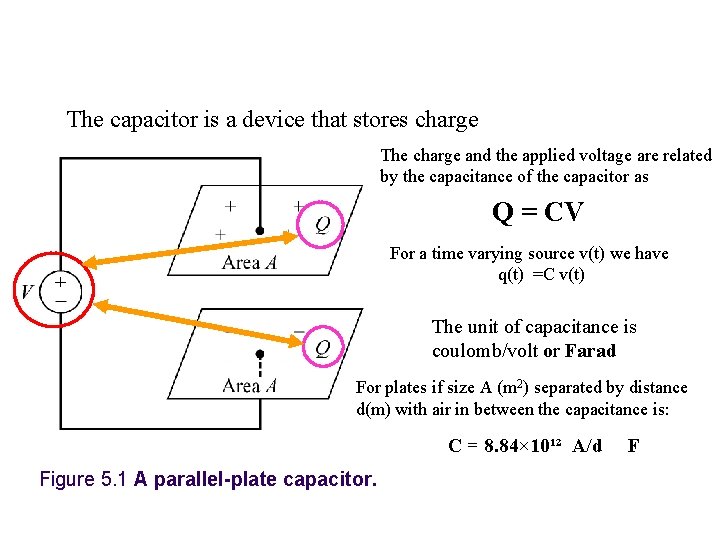
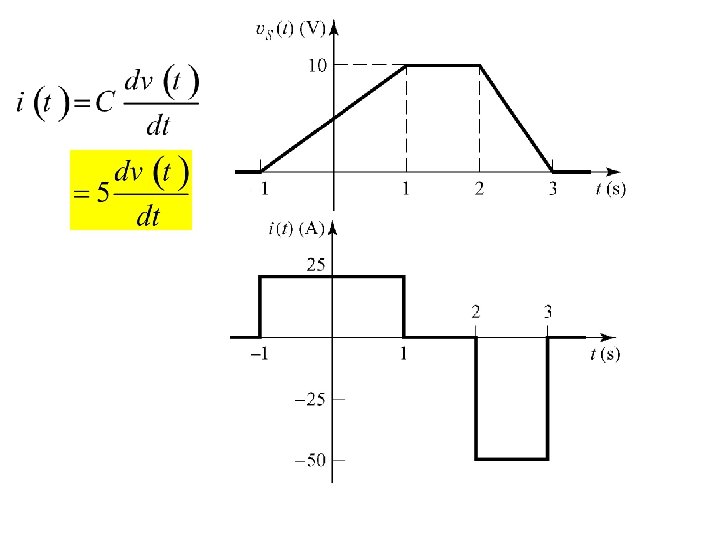
The capacitor is a device that stores charge The charge and the applied voltage are related by the capacitance of the capacitor as Q = CV For a time varying source v(t) we have q(t) =C v(t) The unit of capacitance is coulomb/volt or Farad For plates if size A (m 2) separated by distance d(m) with air in between the capacitance is: C = 8. 84× 10¹² A/d Figure 5. 1 A parallel-plate capacitor. F

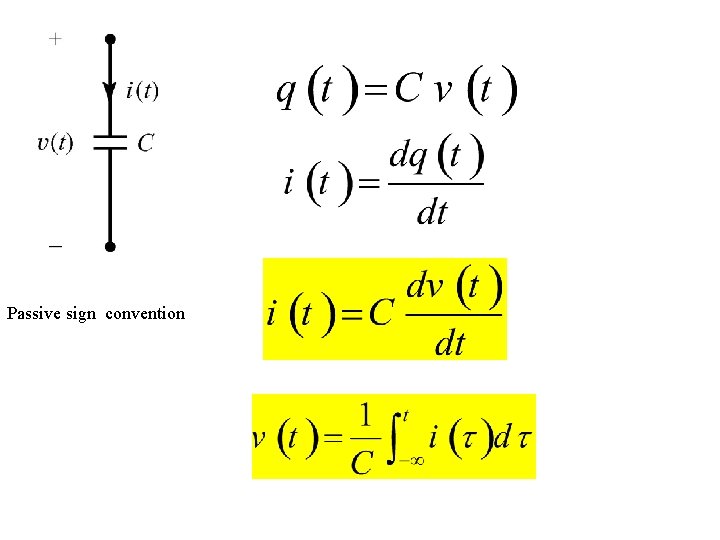
Passive sign convention

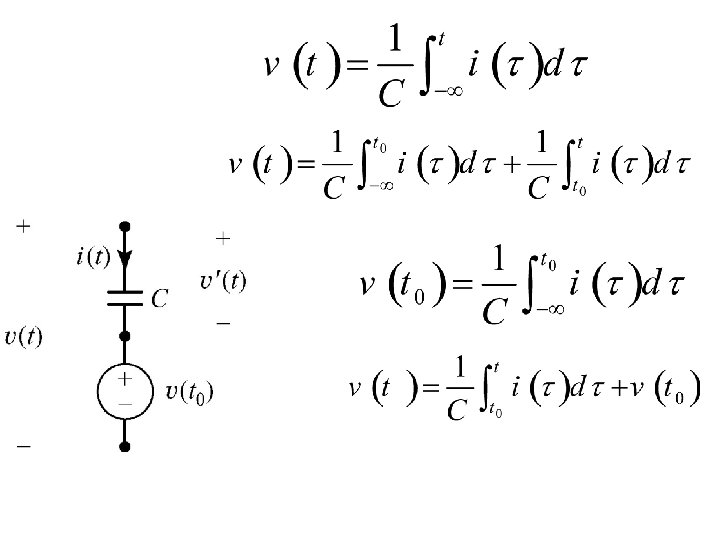
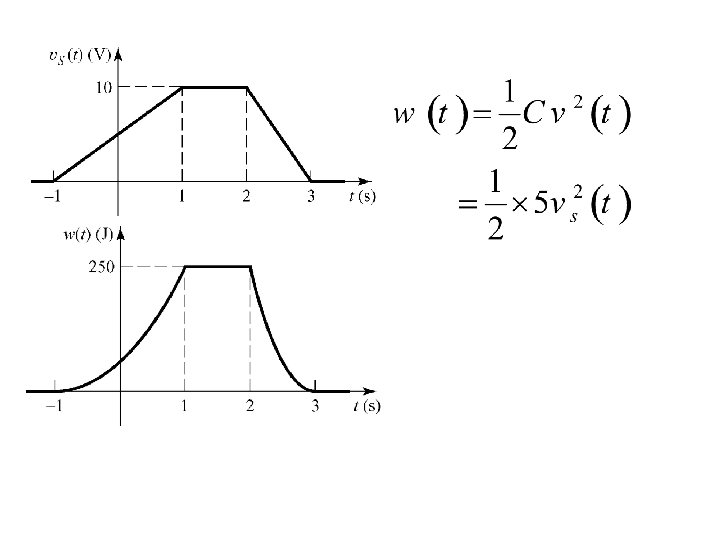
Capacitor Energy The instantaneous power delivered to the capacitor is: The energy stored in a capacitor at a particular time can be found by: Assuming capacitor voltage is zero at

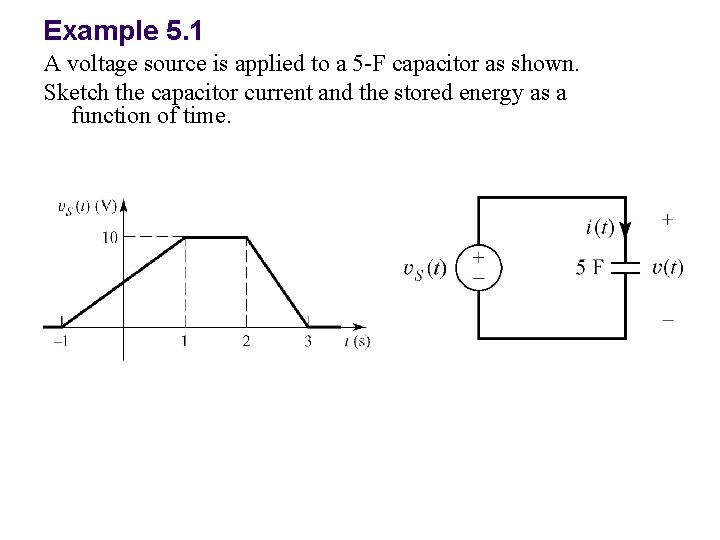
Example 5. 1 A voltage source is applied to a 5 -F capacitor as shown. Sketch the capacitor current and the stored energy as a function of time.

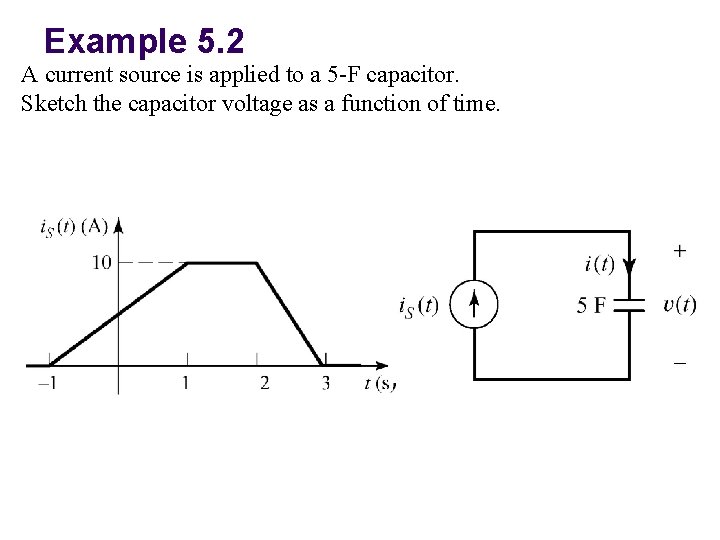
Example 5. 2 A current source is applied to a 5 -F capacitor. Sketch the capacitor voltage as a function of time.

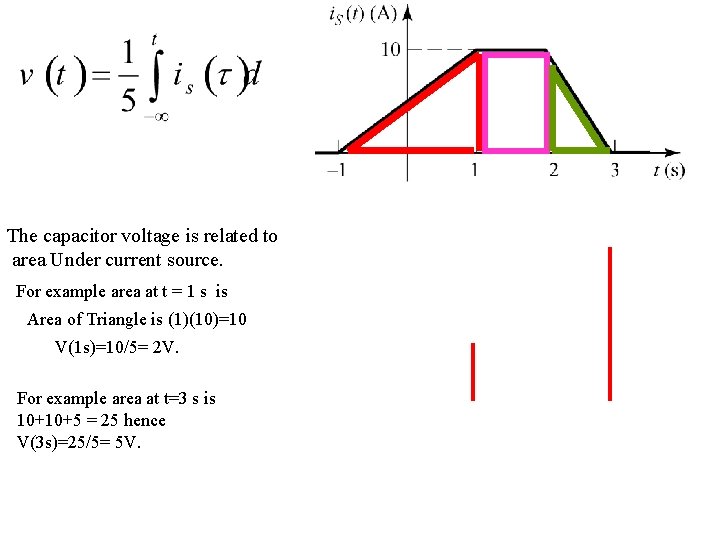
The capacitor voltage is related to area Under current source. For example area at t = 1 s is Area of Triangle is (1)(10)=10 V(1 s)=10/5= 2 V. For example area at t=3 s is 10+10+5 = 25 hence V(3 s)=25/5= 5 V.

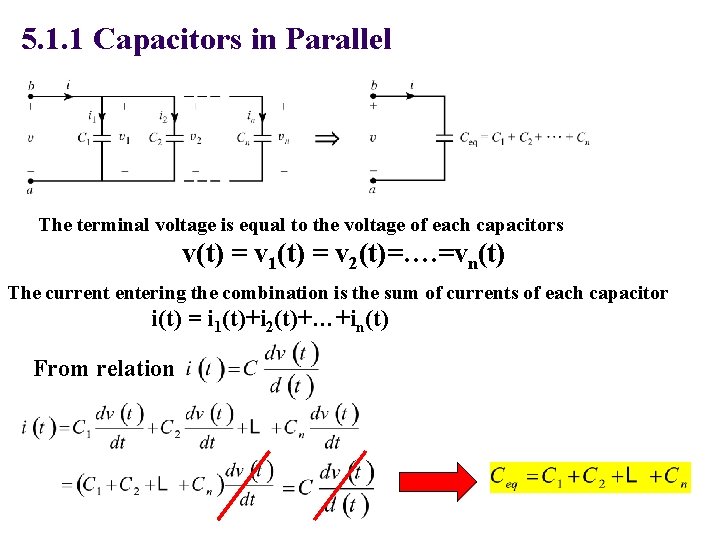
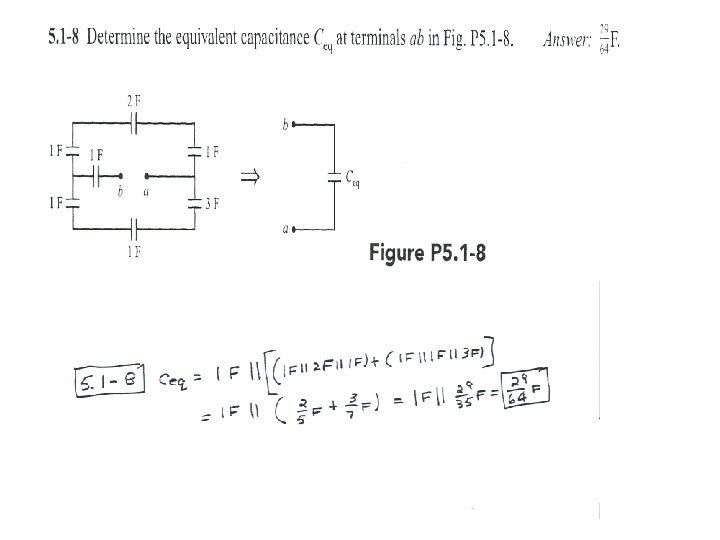
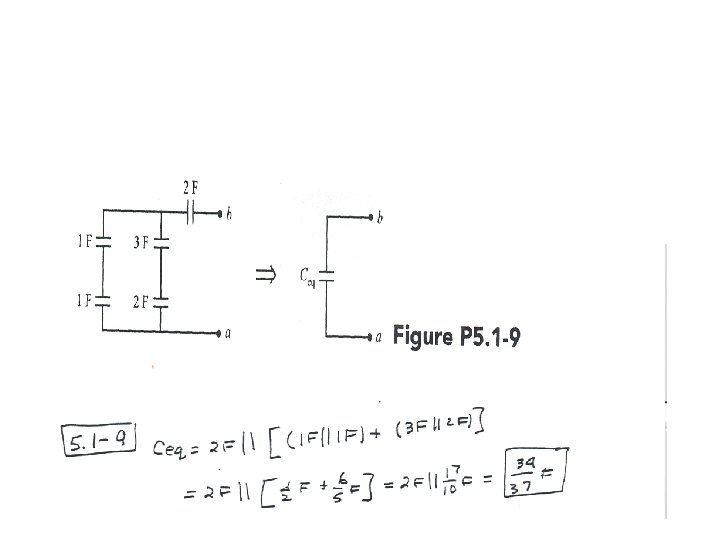
5. 1. 1 Capacitors in Parallel The terminal voltage is equal to the voltage of each capacitors v(t) = v 1(t) = v 2(t)=…. =vn(t) The current entering the combination is the sum of currents of each capacitor i(t) = i 1(t)+i 2(t)+…+in(t) From relation

Capacitors in Series 5. 1. 1 v(t) = v 1(t) + v 2(t) + …. + vn(t) i(t) = i 1(t) = i 2(t) = … = in(t)

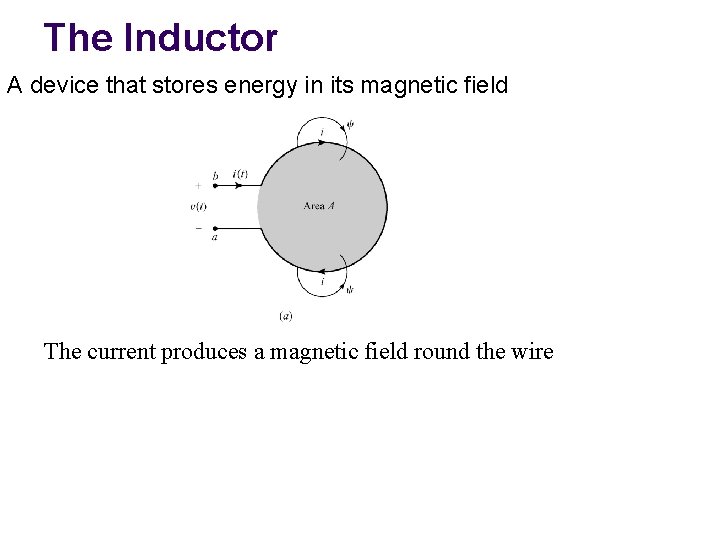
The Inductor A device that stores energy in its magnetic field The current produces a magnetic field round the wire

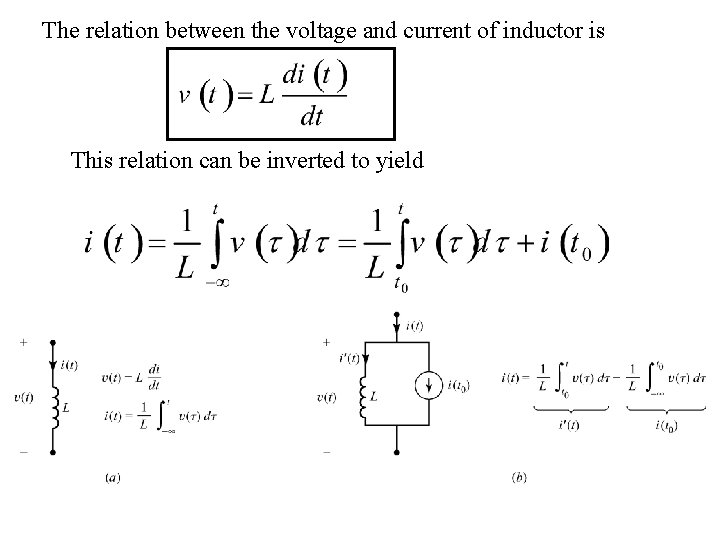
The relation between the voltage and current of inductor is This relation can be inverted to yield

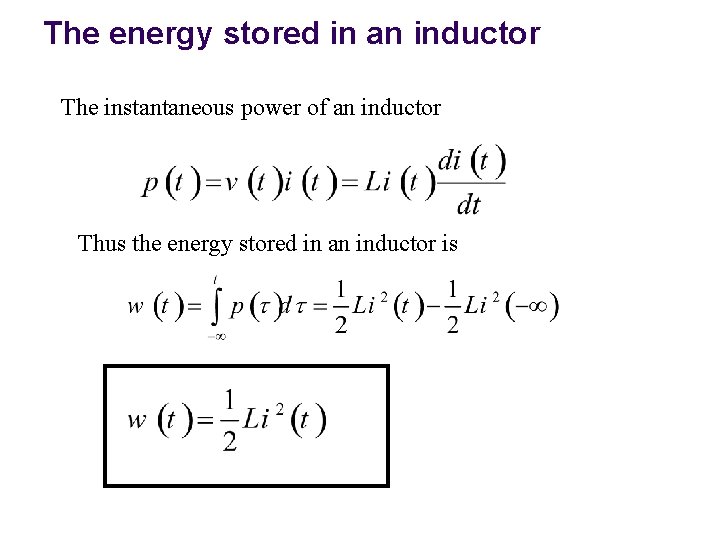
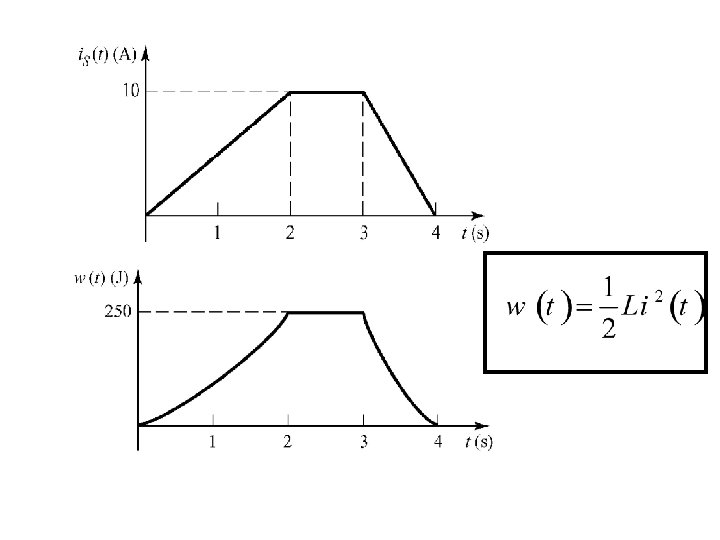
The energy stored in an inductor The instantaneous power of an inductor Thus the energy stored in an inductor is

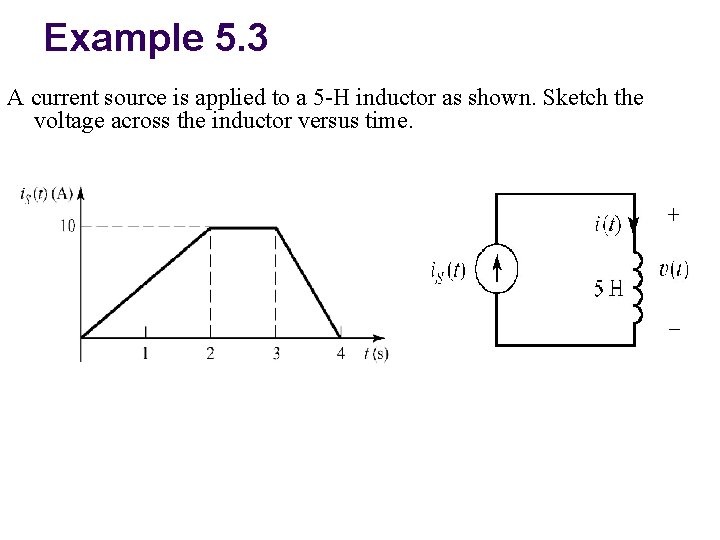
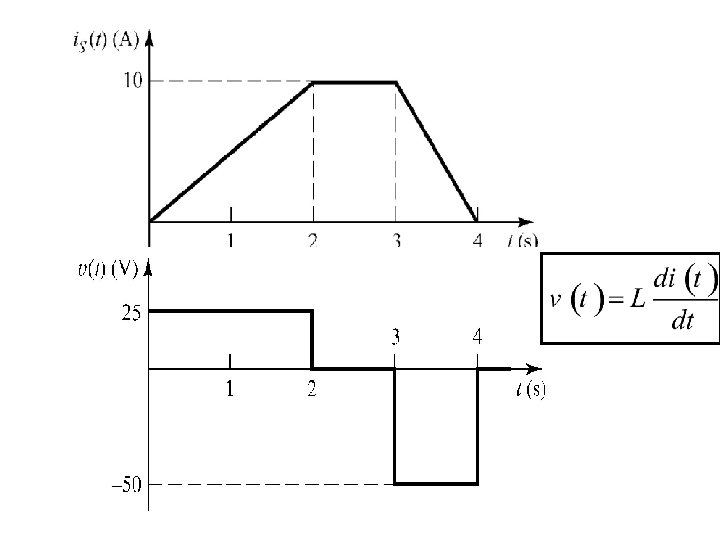
Example 5. 3 A current source is applied to a 5 -H inductor as shown. Sketch the voltage across the inductor versus time.

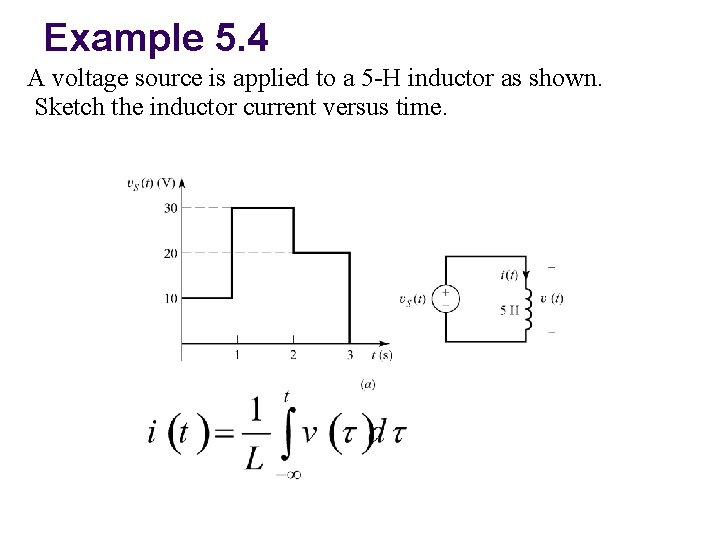
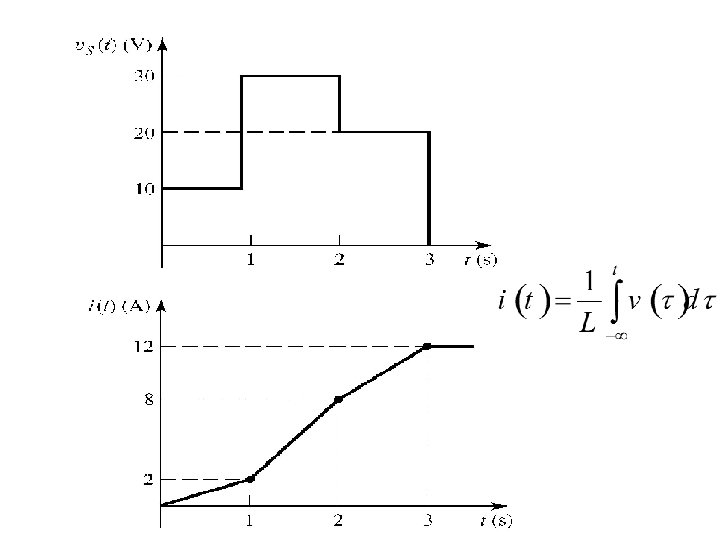
Example 5. 4 A voltage source is applied to a 5 -H inductor as shown. Sketch the inductor current versus time.

Inductors in Series

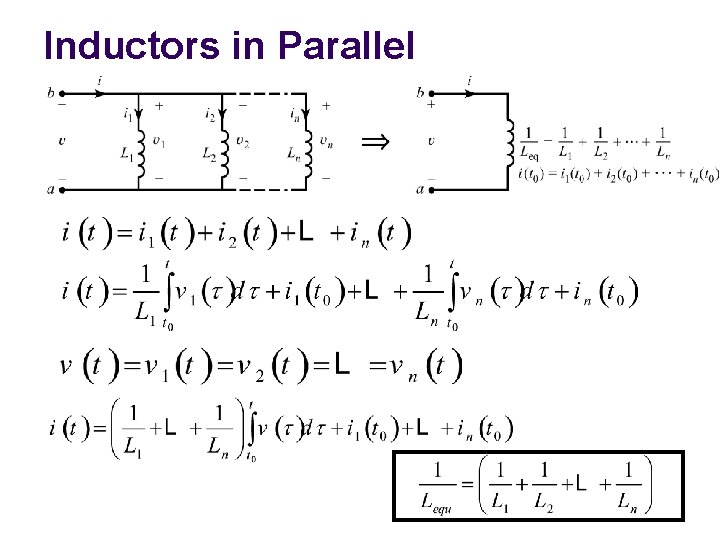
Inductors in Parallel

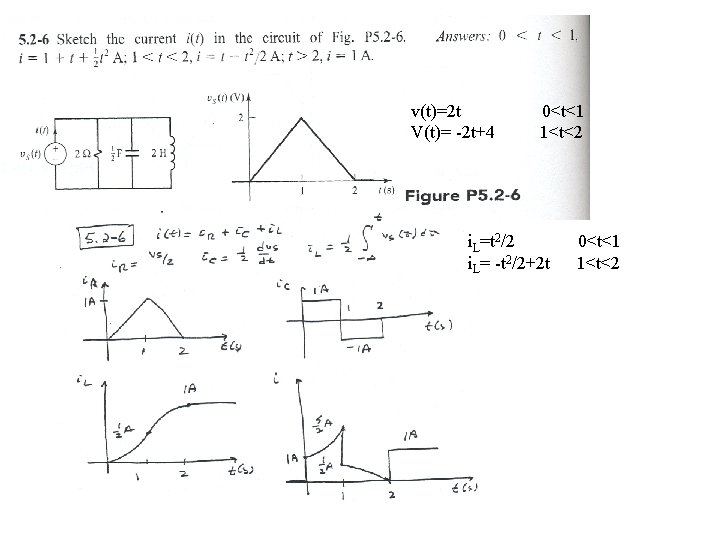
v(t)=2 t V(t)= -2 t+4 0<t<1 1<t<2 i. L=t 2/2 i. L= -t 2/2+2 t 0<t<1 1<t<2