Chapter 5 System Analysis in Domain Transform System

Chapter 5: System Analysis in Domain Transform System Function, Linear Constant Coefficient Different Equation, ROC determination and System Properties, Impulse response classification. 1

Introduction �� �� ℎ[�� ] �� �� • �� [ �� ] is the result of the convolution of �� [�� ] & ℎ[�� ] �� [�� ] = �� [�� ] ∗ ℎ[�� ] • In LTI system, in z-plane, the convolution is equivalent to a multiplication process �� (�� ) = �� (�� )x �� (�� ) 2

System Function H(z) Also called transfer function It is a function in z-domain that relates the input signal x[n] with the output signal y[n] where • For continuous-time systems, differential equation may be solved using Laplace transform • Similarly discrete-time systems result in Difference Equations which may be solved using z-transform • There is a simple relationship for a signal time-shifting properties • This is fundamental for deriving the transfer function of a difference equation which is expressed in terms of the inputoutput signal delays • The transfer function of a discrete time LTI system is the z transform of the system’s impulse response

Example 5. 1 • Determine the system function and the unit sample response of the system described by the difference equation

Example 5. 2 Determine the system function for a) b) c) Construct the Linear Constant Coefficient Difference Equation (LCCDE) of the following system d)

Exercise Obtain the difference equation for (a) (b) (c)

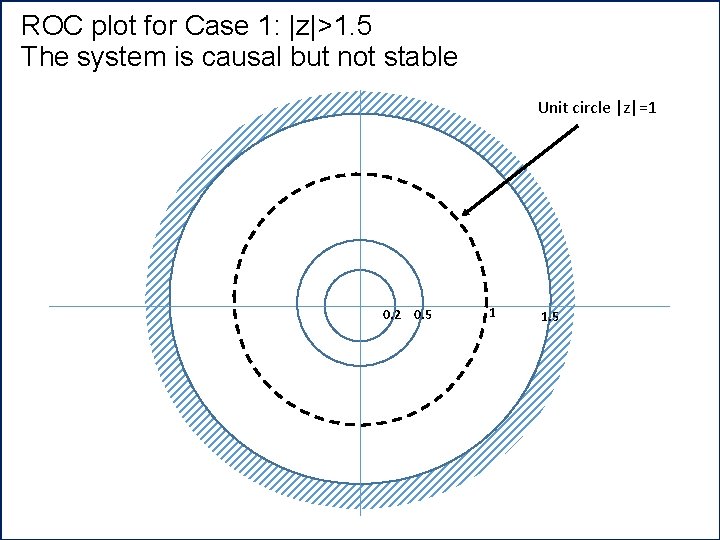
Causality and Stability A discrete time LTI system is causal if and only if 1. The ROC is the exterior of a circle outside the outermost pole 2. If H(z) is expressed as ratio of polynomial in ‘z’, the order of the numerator cannot be greater than the order of the denumerator An LTI system is stable is 1. It’s system function H(z) includes the unit circle (|z|=1) 2. A causal LTI system is stable if and only if all the poles of H(z) lies inside the unit circle

Example 5. 3 With the aid of ROC plot, discuss the various cases for stability and causality for the system below. For each case, evaluate the impulse response, h[n] Solution:

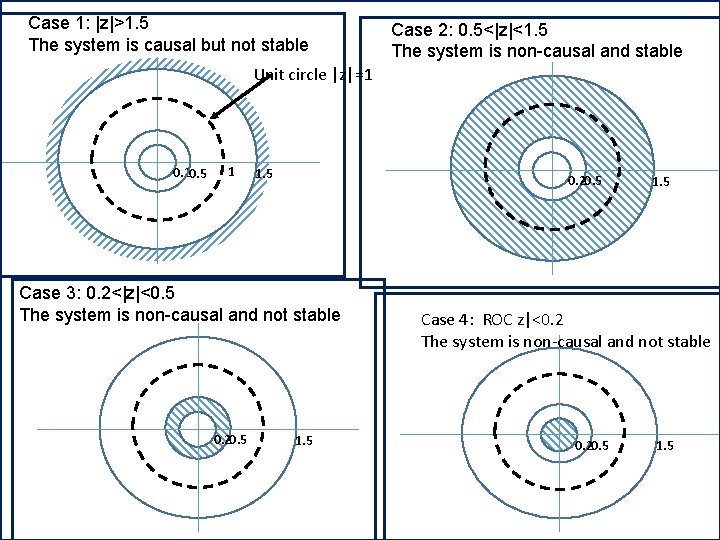
3 poles: z=1. 5, z=0. 2

ROC plot for Case 1: |z|>1. 5 The system is causal but not stable Unit circle |z|=1 0. 2 0. 5 1 1. 5

Evaluate the impulse response, h[n] Causal

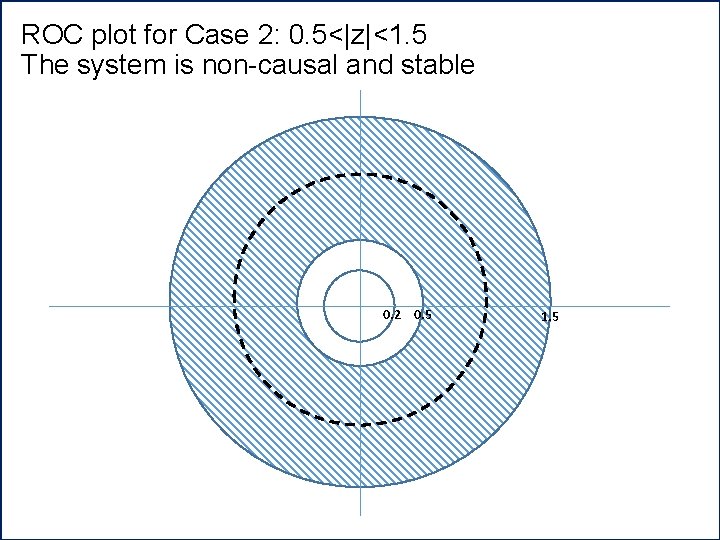
ROC plot for Case 2: 0. 5<|z|<1. 5 The system is non-causal and stable 0. 2 0. 5 1. 5

• System is stable because ROC includes the unit circle |z|=1 • System is non-causal at pole 1. 5 • Evaluate h[n] Anti-causal Causal signal Anti-Causal signal

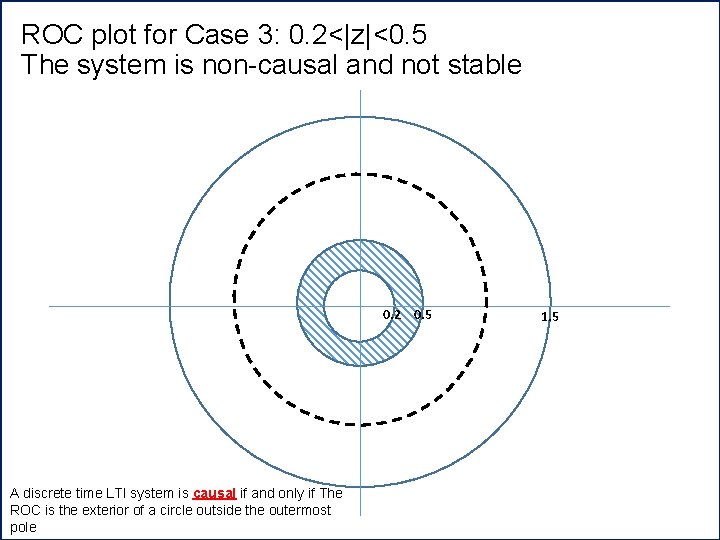
ROC plot for Case 3: 0. 2<|z|<0. 5 The system is non-causal and not stable 0. 2 0. 5 A discrete time LTI system is causal if and only if The ROC is the exterior of a circle outside the outermost pole 1. 5

• System is not stable because ROC does not includes the unit circle |z|=1 • System is non-causal at pole 0. 5 and 1. 5 Anti-causal

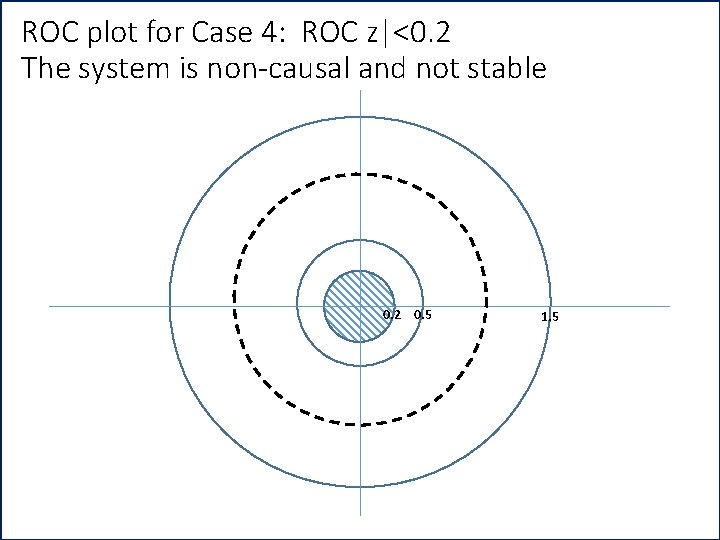
ROC plot for Case 4: ROC z|<0. 2 The system is non-causal and not stable 0. 2 0. 5 1. 5

• System is not stable because ROC does not includes the unit circle |z|=1 • System is non-causal at pole 0. 2, 0. 5 and 1. 5 Anti-causal

Case 1: |z|>1. 5 The system is causal but not stable Case 2: 0. 5<|z|<1. 5 The system is non-causal and stable Unit circle |z|=1 0. 20. 5 1 1. 5 0. 20. 5 Case 3: 0. 2<|z|<0. 5 The system is non-causal and not stable 0. 20. 5 1. 5 Case 4: ROC z|<0. 2 The system is non-causal and not stable 0. 20. 5 1. 5

Impulse Response for Case 1: |z|>1. 5 , The system is causal but not stable Impulse Response for Case 2: 0. 5<|z|<1. 5 The system is non-causal at pole 1. 5 and stable Impulse Response for Case 3: 0. 2<|z|<0. 5 The system is non-causal at pole 0. 5 and 1. 5 and not stable Impulse Response for Case 4: ROC z|<0. 2 The system is non-causal at pole 0. 2, 0. 5 and 1. 5 and not stable