Chapter 5 Synchronous Sequential Circuits 1 2 Logic

Chapter 5 Synchronous Sequential Circuits 1

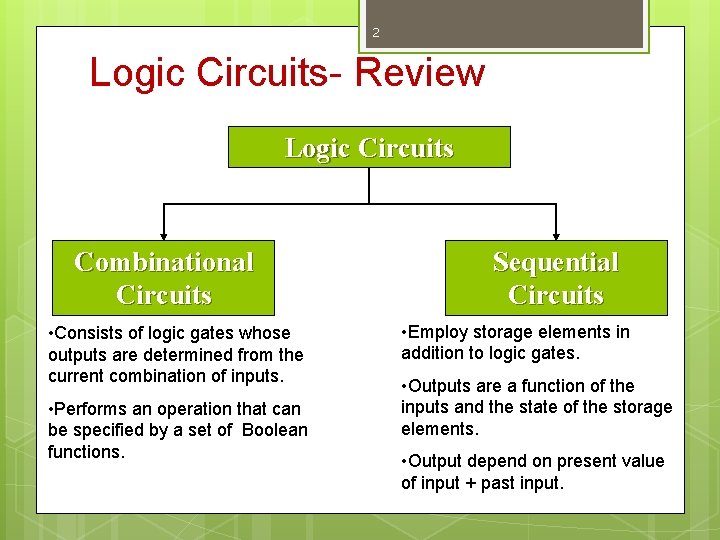
2 Logic Circuits- Review Logic Circuits Combinational Circuits • Consists of logic gates whose outputs are determined from the current combination of inputs. • Performs an operation that can be specified by a set of Boolean functions. Sequential Circuits • Employ storage elements in addition to logic gates. • Outputs are a function of the inputs and the state of the storage elements. • Output depend on present value of input + past input.

3 Overview Storage Elements and Analysis Introduction to sequential circuits Types of sequential circuits Storage elements Latches Flip-flops Sequential State circuit analysis tables State diagrams

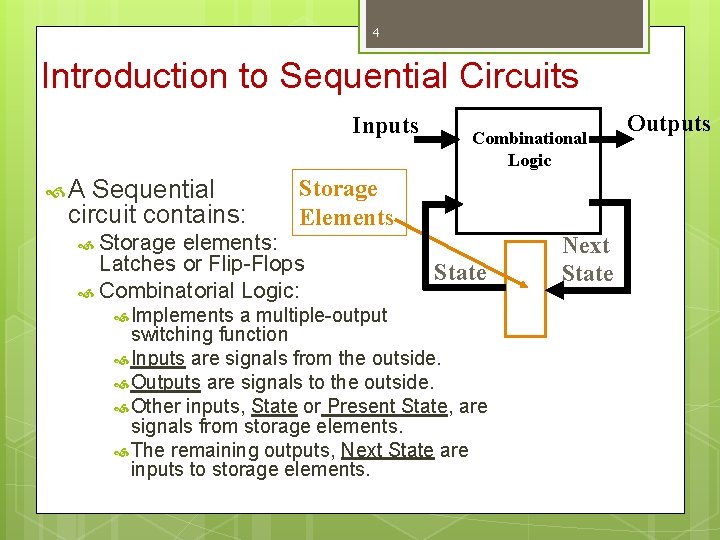
4 Introduction to Sequential Circuits Inputs A Sequential circuit contains: Combinational Logic Storage Elements Storage elements: Latches or Flip-Flops Combinatorial Logic: Implements State a multiple-output switching function Inputs are signals from the outside. Outputs are signals to the outside. Other inputs, State or Present State, are signals from storage elements. The remaining outputs, Next State are inputs to storage elements. Next State Outputs

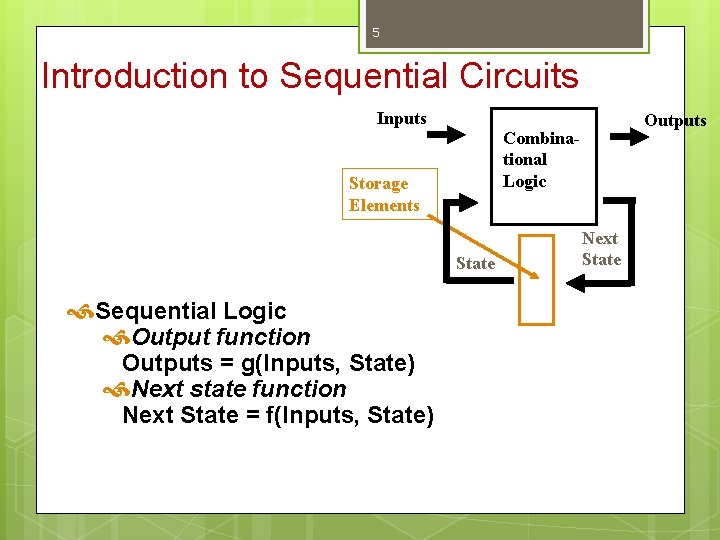
5 Introduction to Sequential Circuits Inputs Combinational Logic Storage Elements State Sequential Logic Output function Outputs = g(Inputs, State) Next state function Next State = f(Inputs, State) Outputs Next State

6 Types of Sequential Circuits Depends on the times at which: storage elements observe their inputs, and storage elements change their state Synchronous Behavior defined from knowledge of its signals at discrete instances of time Storage elements observe inputs and can change state only in relation to a timing signal (clock pulses from a clock) Asynchronous Behavior defined from knowledge of inputs at any instant of time and the order in continuous time in which inputs change If clock just regarded as another input, all circuits are asynchronous!

7 5. 3 Storage Elements : Latches Storage elements Maintain a binary state (0 or 1) indefinitely as long as power is delivered to the circuit Switch states (0 1 or 1 0) when directed by an input signal Most basic storage element Used mainly to construct Flip-Flops Asynchronous storage circuit Types of latches: SR Latches S`R` Latches D Latches X=X

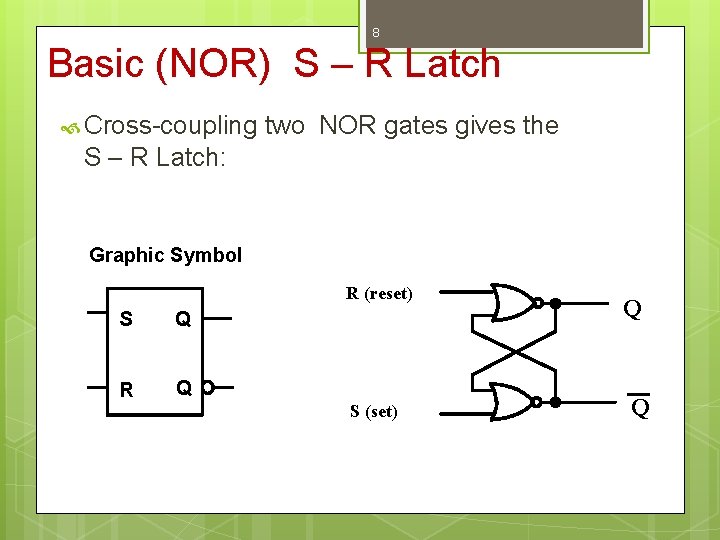
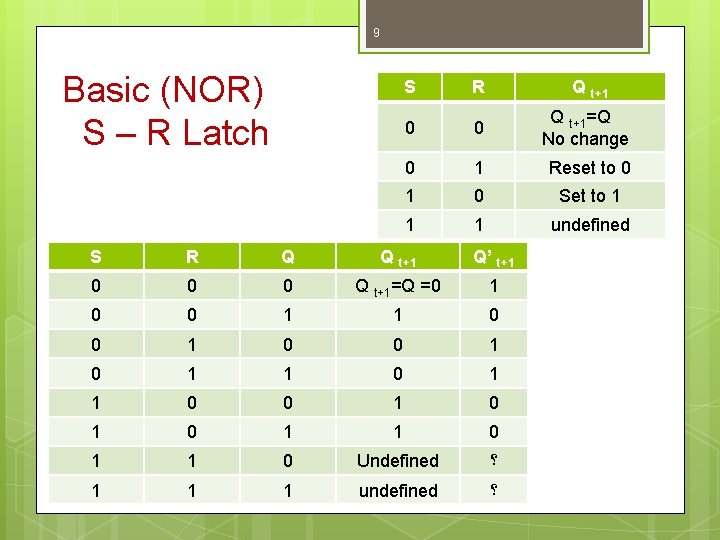
8 Basic (NOR) S – R Latch Cross-coupling two NOR gates gives the S – R Latch: Graphic Symbol R (reset) S Q R Q S (set) Q Q

9 Basic (NOR) S – R Latch S R Q t+1 0 0 Q t+1=Q No change 0 1 Reset to 0 1 0 Set to 1 1 1 undefined S R Q Q t+1 Q’ t+1 0 0 0 Q t+1=Q =0 1 0 0 1 1 0 0 1 0 1 1 0 Undefined ؟ 1 1 1 undefined ؟

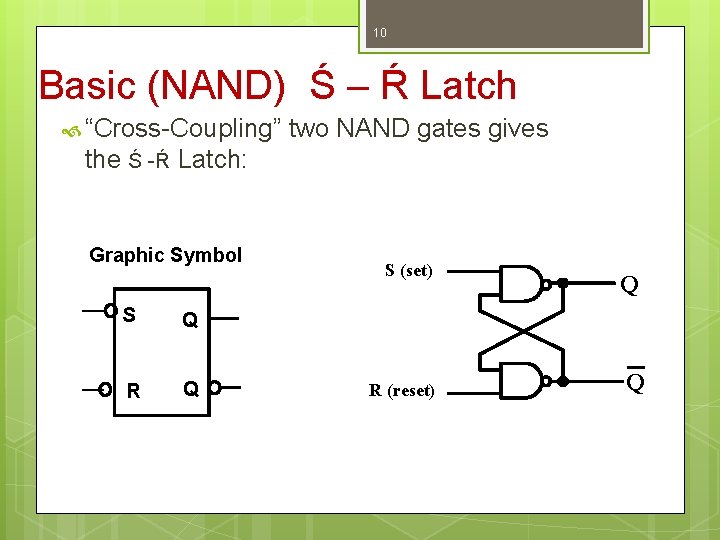
10 Basic (NAND) Ś – Ŕ Latch “Cross-Coupling” two NAND gates gives the Ś -Ŕ Latch: Graphic Symbol S Q R Q S (set) R (reset) Q Q

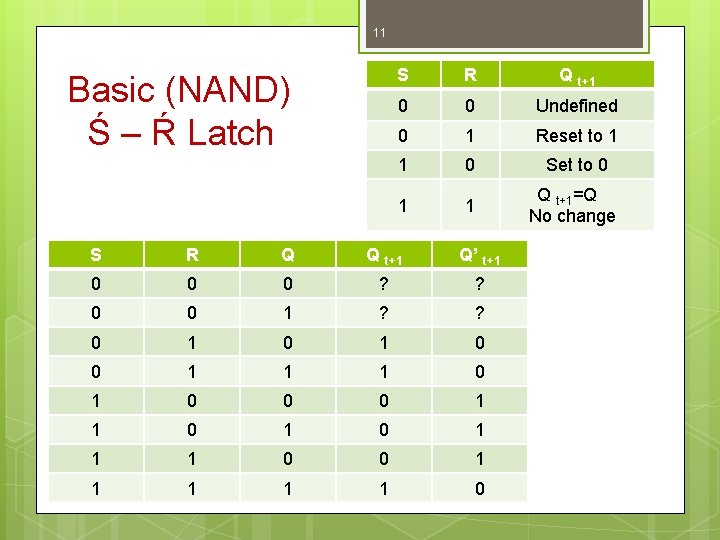
11 Basic (NAND) Ś – Ŕ Latch S R Q t+1 0 0 Undefined 0 1 Reset to 1 1 0 Set to 0 1 1 Q t+1=Q No change S R Q Q t+1 Q’ t+1 0 0 0 ? ? 0 0 1 ? ? 0 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0

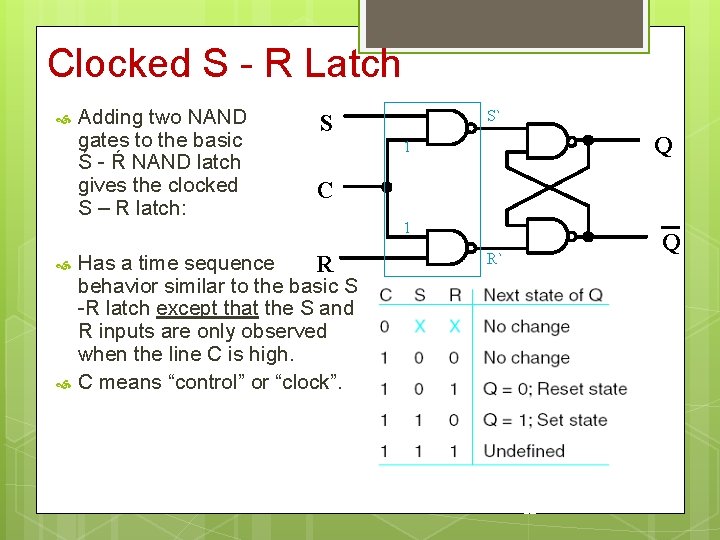
Clocked S - R Latch Adding two NAND gates to the basic Ś - Ŕ NAND latch gives the clocked S – R latch: Q 1 C Has a time sequence R behavior similar to the basic S -R latch except that the S and R inputs are only observed when the line C is high. C means “control” or “clock”. S` S 1 Q R` 12

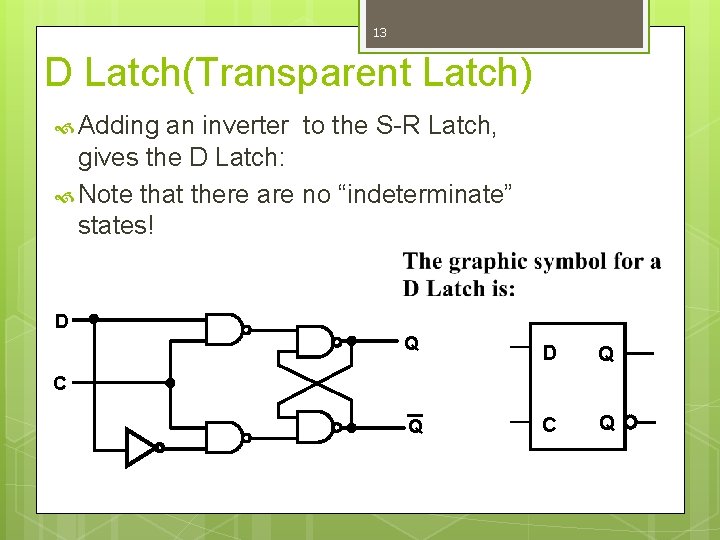
13 D Latch(Transparent Latch) Adding an inverter to the S-R Latch, gives the D Latch: Note that there are no “indeterminate” states! D Q Q C

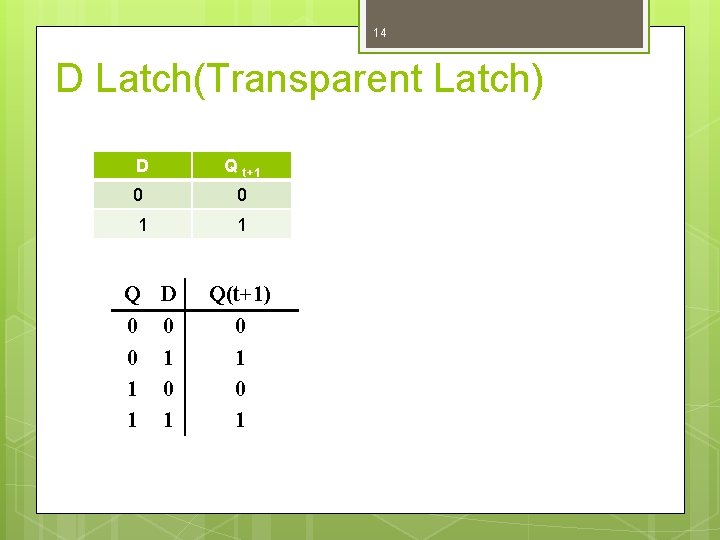
14 D Latch(Transparent Latch) D Q t+1 0 0 1 1 Q D 0 0 0 1 1 Q(t+1) 0 1

Chapter 5: Sequential Circuits 5. 4: Flip-Flops 15

16 Flip-Flops The latch timing problem Master-slave flip-flop Edge-triggered flip-flop Other flip-flops - JK flip-flop - T flip-flop

The Latch Timing Problem In a sequential circuit, paths may exist through combinational logic: From one storage element to another From a storage element back to the same storage element The combinational logic between a latch output and a latch input may be as simple as an interconnect For a clocked D-latch, the output Q depends on the input D whenever the clock input C has value 1 17

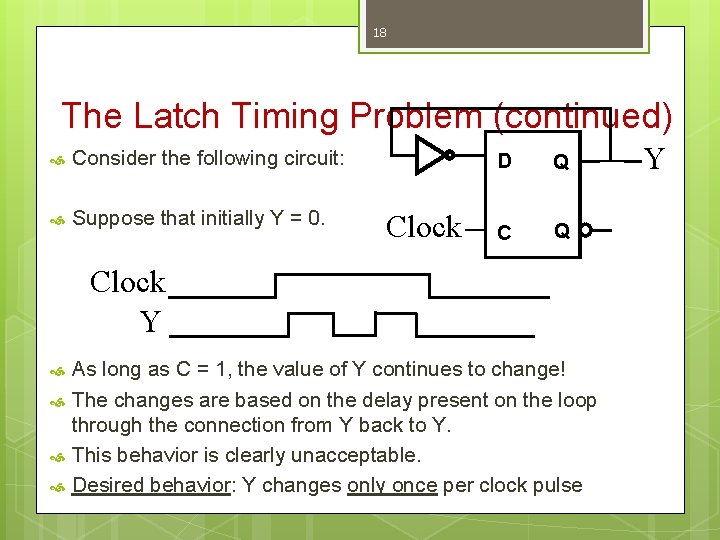
18 The Latch Timing Problem (continued) Consider the following circuit: Suppose that initially Y = 0. Clock D Q Clock Y As long as C = 1, the value of Y continues to change! The changes are based on the delay present on the loop through the connection from Y back to Y. This behavior is clearly unacceptable. Desired behavior: Y changes only once per clock pulse Y

19 The Latch Timing Problem (continued) A solution to the latch timing problem is to break the closed path from Y to Y within the storage element The commonly-used, path-breaking solutions replace the clocked D-latch with: a master-slave flip-flop an edge-triggered flip-flop

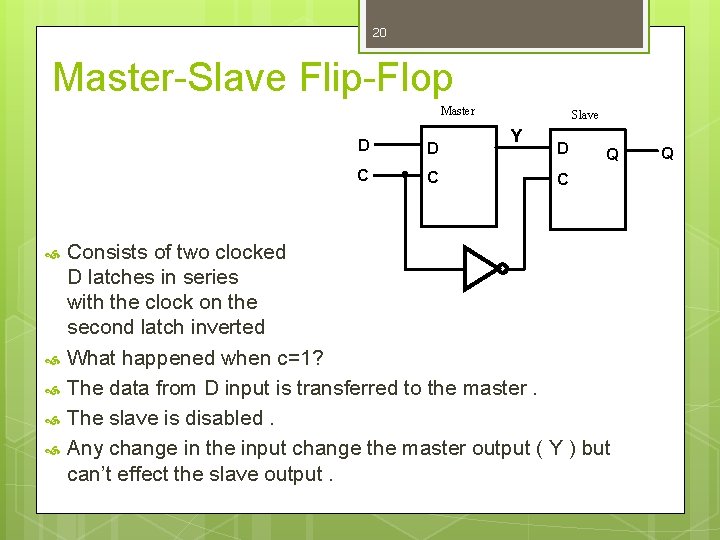
20 Master-Slave Flip-Flop Master D D C C Slave Y D Q C Consists of two clocked D latches in series with the clock on the second latch inverted What happened when c=1? The data from D input is transferred to the master. The slave is disabled. Any change in the input change the master output ( Y ) but can’t effect the slave output. Q

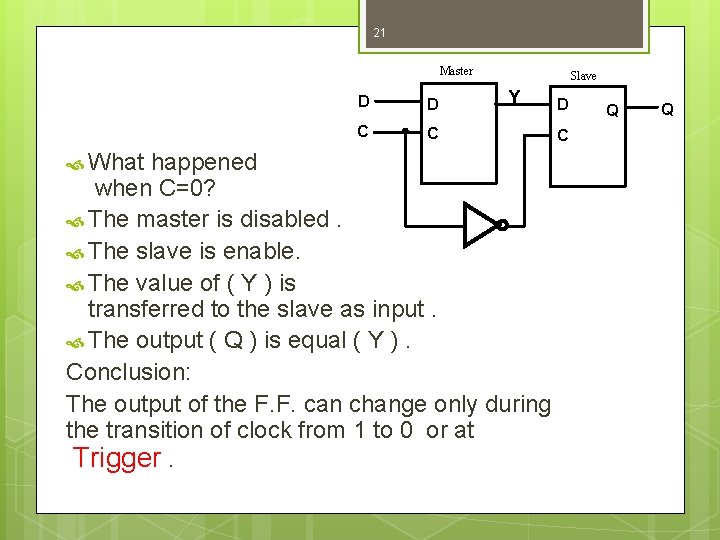
21 Master What D D C C Slave Y happened when C=0? The master is disabled. The slave is enable. The value of ( Y ) is transferred to the slave as input. The output ( Q ) is equal ( Y ). Conclusion: The output of the F. F. can change only during the transition of clock from 1 to 0 or at Trigger. D C Q Q

22 Timing

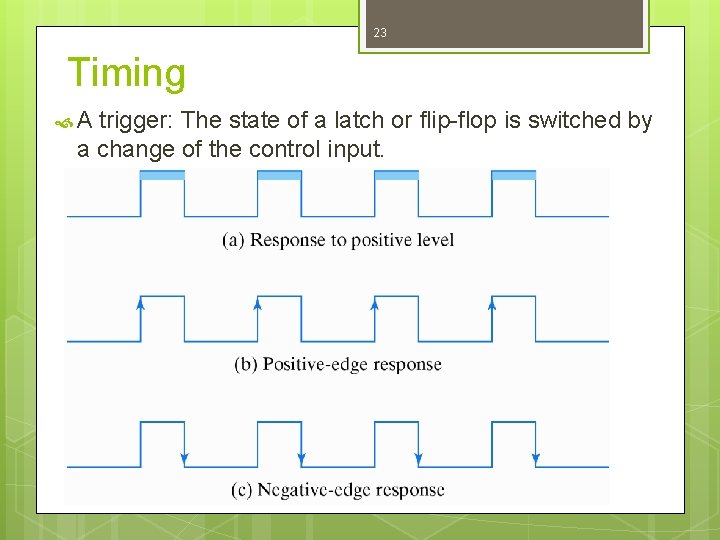
23 Timing A trigger: The state of a latch or flip-flop is switched by a change of the control input.

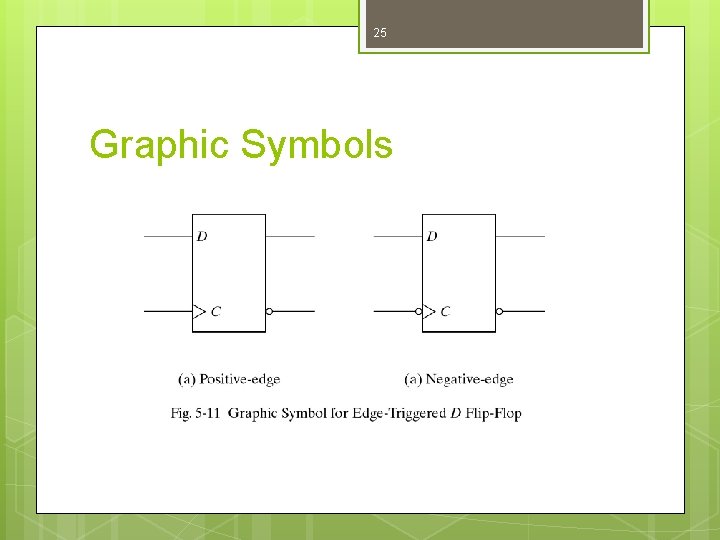
24 Graphic Symbols

25 Graphic Symbols

26 Other flip-flops • • • Other F-Fs can be built using D F-F There are four operation on a F-F - set to 1 - Reset to 0 - toggle ( complement ) of Q - nothing There are tow F-F - JK F-F - T F-F

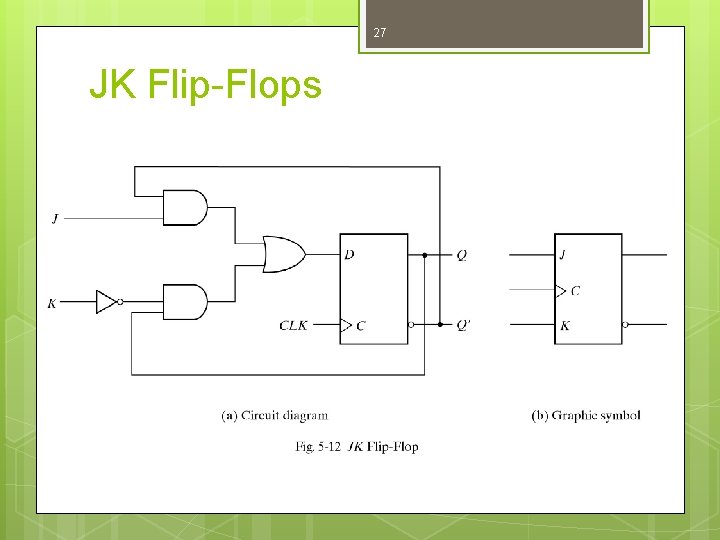
27 JK Flip-Flops

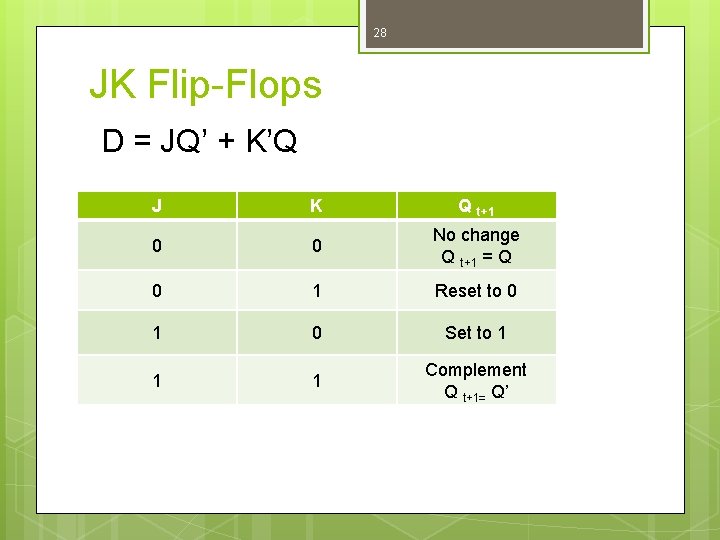
28 JK Flip-Flops D = JQ’ + K’Q J K Q t+1 0 0 No change Q t+1 = Q 0 1 Reset to 0 1 0 Set to 1 1 1 Complement Q t+1= Q’

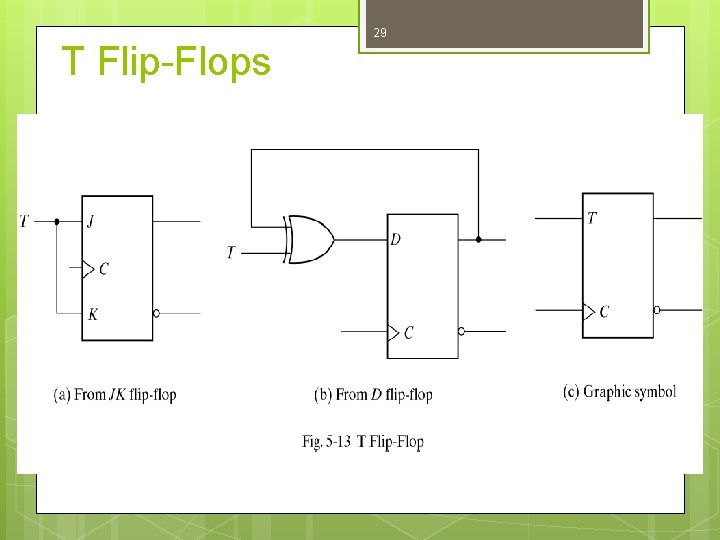
T Flip-Flops 29

30 T Flip-Flops

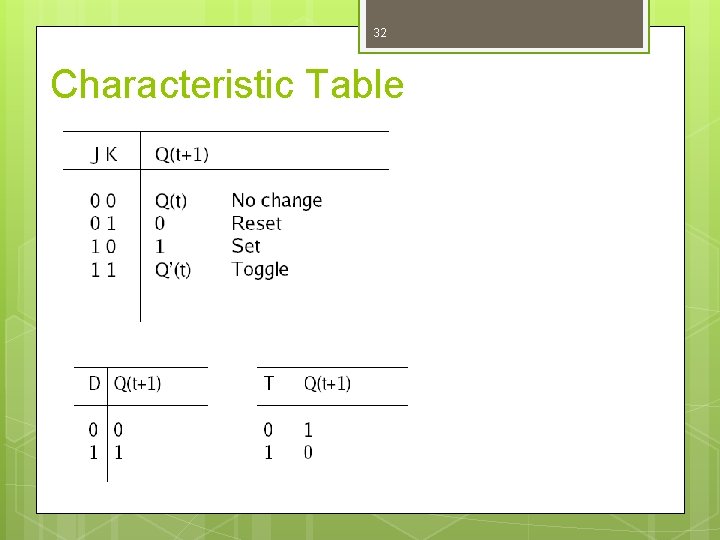
31 Characteristic Table

32 Characteristic Table

33 Characteristic Equations

34

35 State Equation

36 State Equation

37

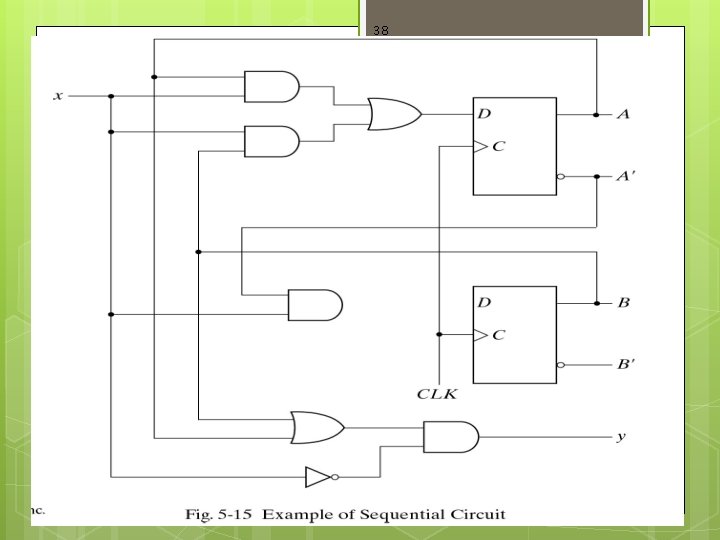
38

39 Analysis This circuit consist of : 2 D F-F A and B Input x Output Y Qt+1 = D A= D A B = D B

40

41

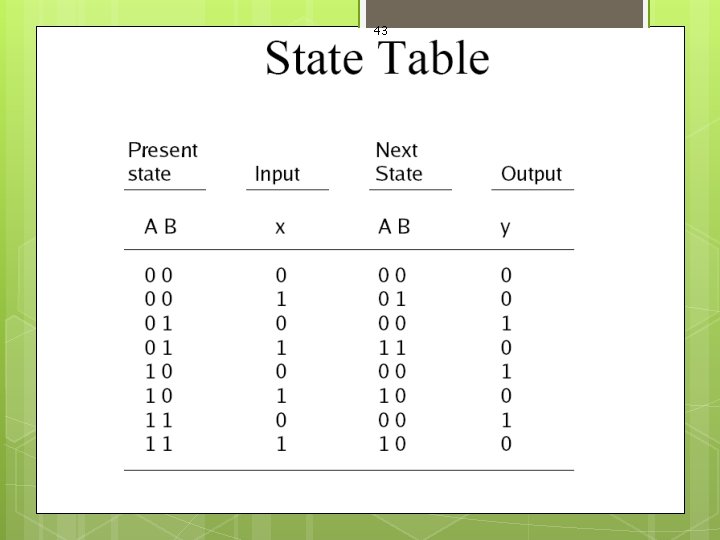
42 State Table

43

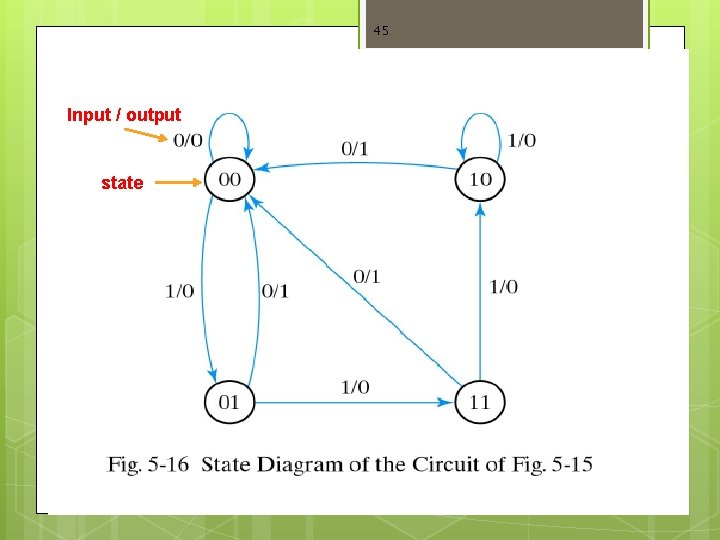
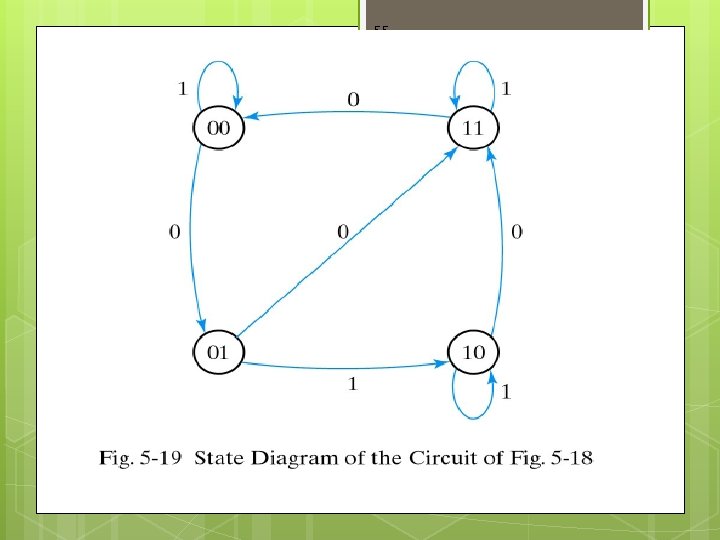
44 State Diagram

45 Input / output state

46

47

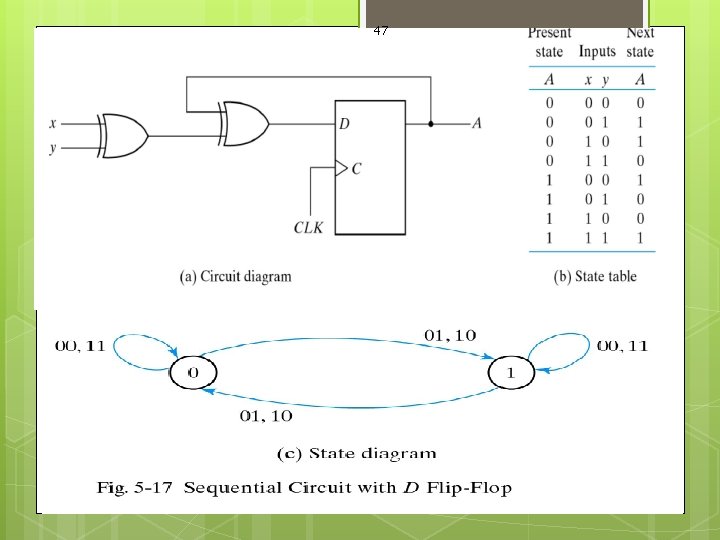
Analysis 1 D F-F ( A ) 2 Input X , Y Qt+1 = D D = A X y 48

49

50

51

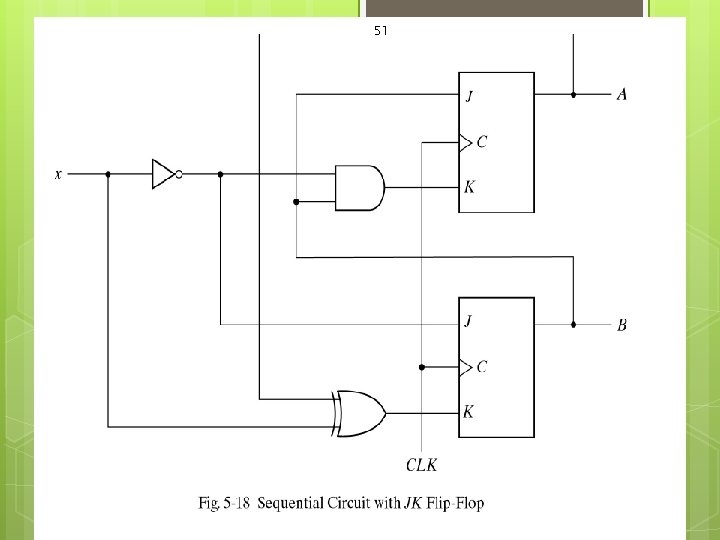
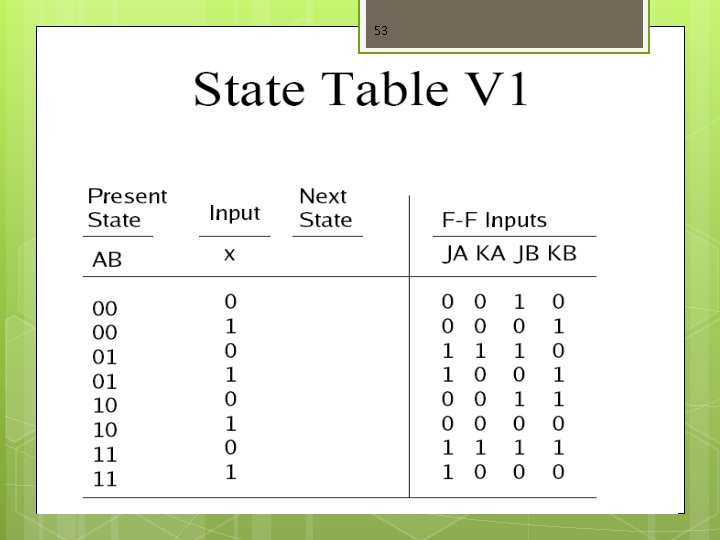
Analysis 2 JK F-F (A , B) Input x Q t+1 = JQ’ + K’Q 52

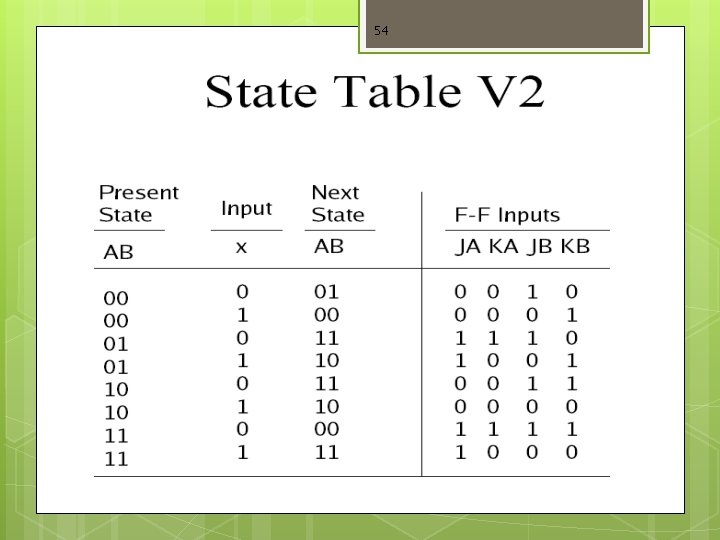
53

54

55

56

57

58

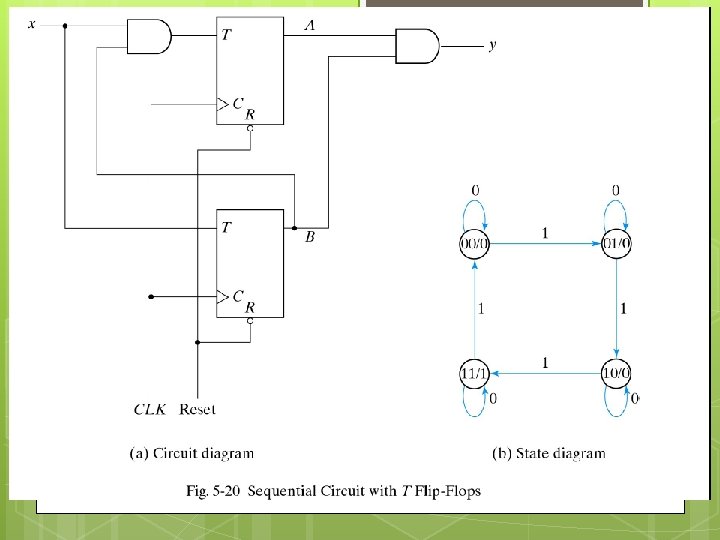
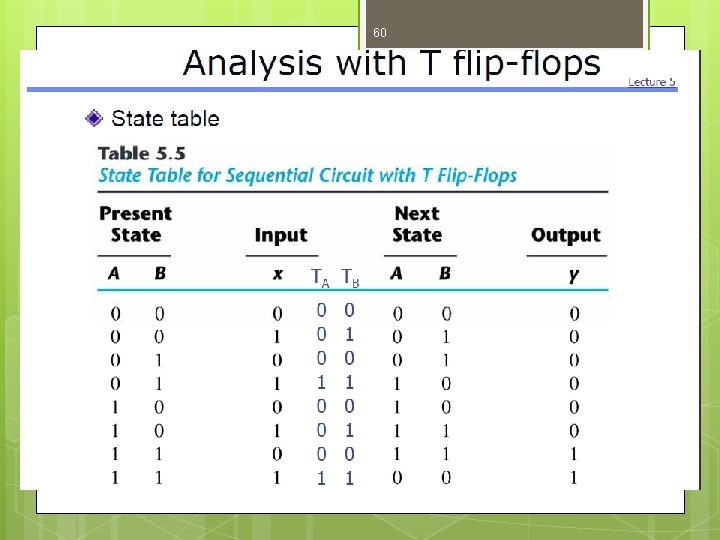
Analysis 2 59 T F-F ( A, B ) 1 input X 1 output Y Qt+1 = T Q The input equations are T_A = BX T_B = X The out put equation is Y = AB The characteristic equations are : At+1 = T_A A = BX(A’) + (BX)’A = A’BX + AB’ + AX’ Bt+1 = X B

60

61 Good Luck