Chapter 5 Stresses in beams Stresses in Beams

Chapter 5 Stresses in beams

(Stresses in Beams) 第五章 弯曲应力 (Stresses in beams) § 5 -1 引言 ( Introduction) § 5 -2 纯弯曲时的正应力 (Normal stresses in pure beams ) § 5 -3 横力弯曲时的正应力(Normal stresses in transverse bending ) § 5 -4 梁的切应力及强度条件 (Shear stresses stresse in beams and strength condition) § 5 -5 提高梁强度的主要措施(Measures to strengthen the strength of beams)



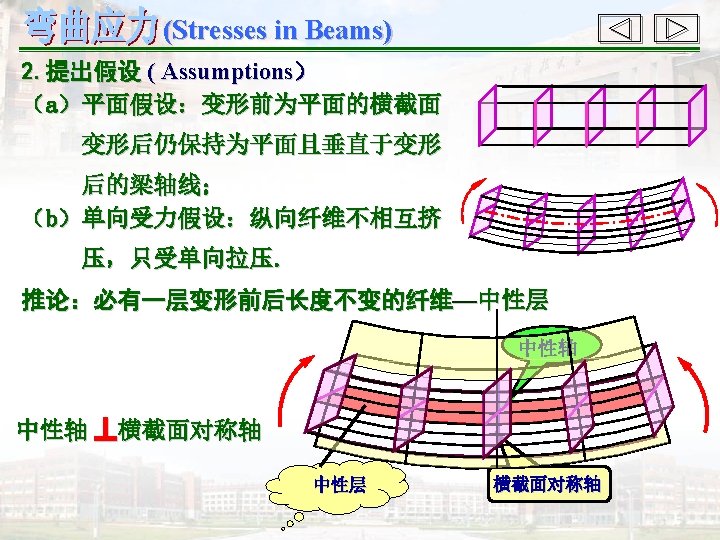
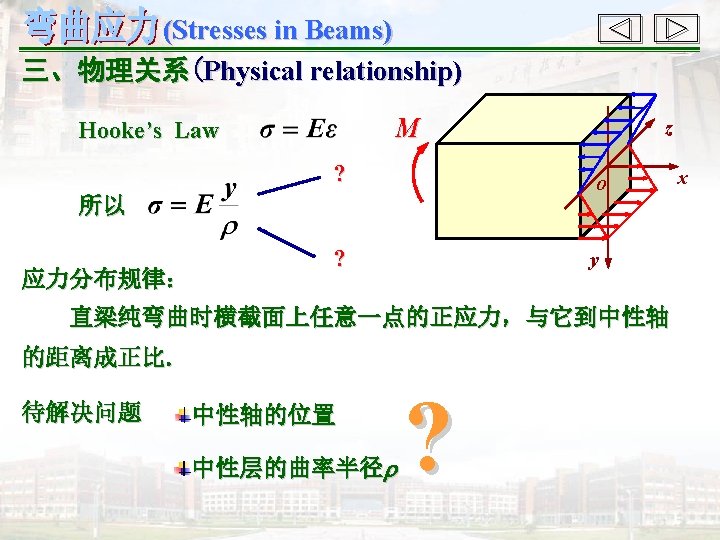
(Stresses in Beams) § 5 -2 纯弯曲时的正应力 (Normal stresses in pure beams ) deformation geometric relationship physical relationship Examine the deformation, then propose the hypothesis Distribution regularity of deformation Distribution regularity of stress static relationship Establish the formula 变 形 几 何 关 系 物 理 关 系 静 力 关 系 观察变形, 提出假设 变形的分布规律 应力的分布规律 建立公式







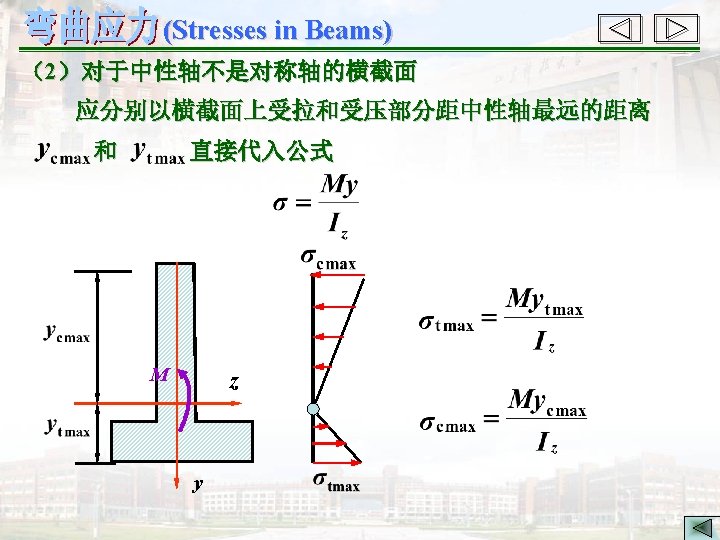


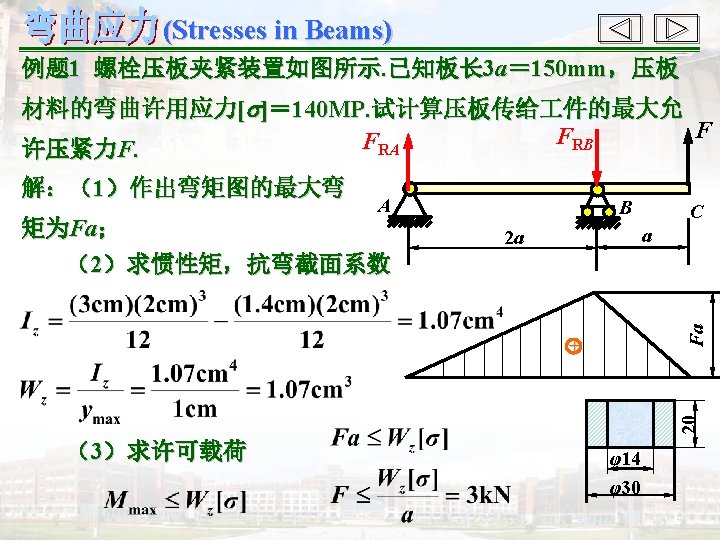
(Stresses in Beams) 二、公式的应用范围 (The applicable range of the flexure formula ) 1. 在弹性范围内 (All stresses in the beam are below the proportional limit) 2. 具有切应力的梁(The beam with the shear stress) 3. 平面弯曲(Plane bending) 4. 直梁(Straight beams) 三、强度条件(Strength condition) 梁内的最大 作应力不超过材料的许用应力. 1. 数学表达式(Mathematical formula)

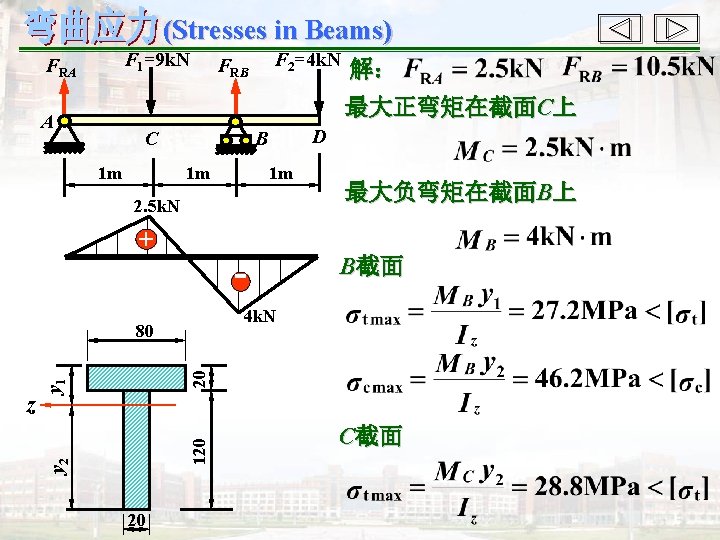
(Stresses in Beams) F 1=9 k. N FRA F 2=4 k. N FRB 解: 最大正弯矩在截面C上 A C 1 m D B 1 m 1 m 2. 5 k. N 最大负弯矩在截面B上 + 4 k. N y 2 120 y 1 20 80 z B截面 20 C截面


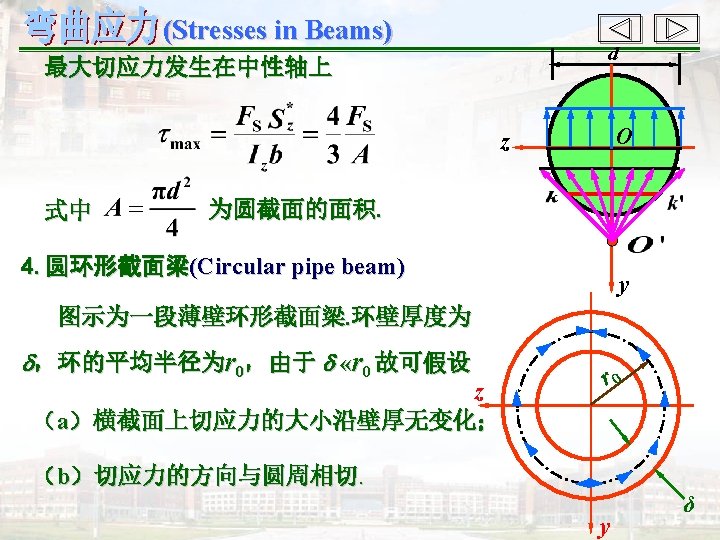
(Stresses in Beams) § 5 -4 梁的切应力及强度条件(Shear stresses in beams and strength condition) 一、梁横截面上的切应力(Shear stresses in beams) 1. 矩形截面梁(Beam of rectangular cross section) (1)两个假设(Two assumptions) (a)切应力与剪力平行; (b)切应力沿截面宽度均匀分布 (距中性轴等距离处切应力相等). F 1 F 2 q(x)
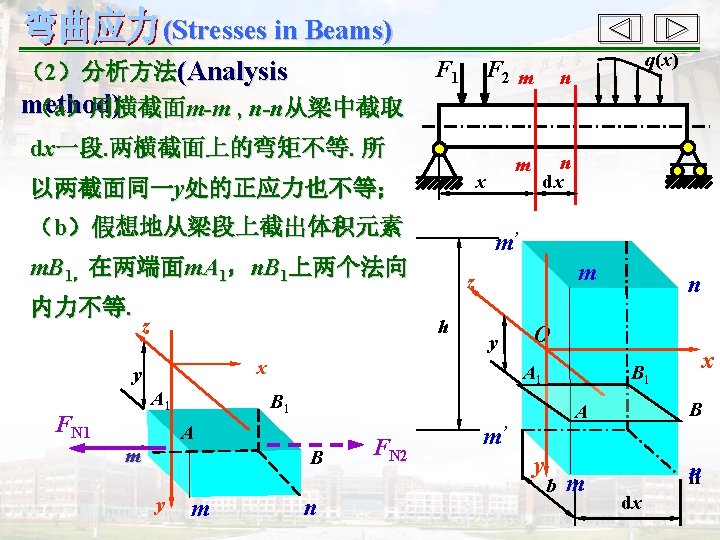



(Stresses in Beams) z x y A 1 d. FS’ FN 2 A m’ B 1 B FN 1 由平衡方程 y 化简后得 A 1 m n





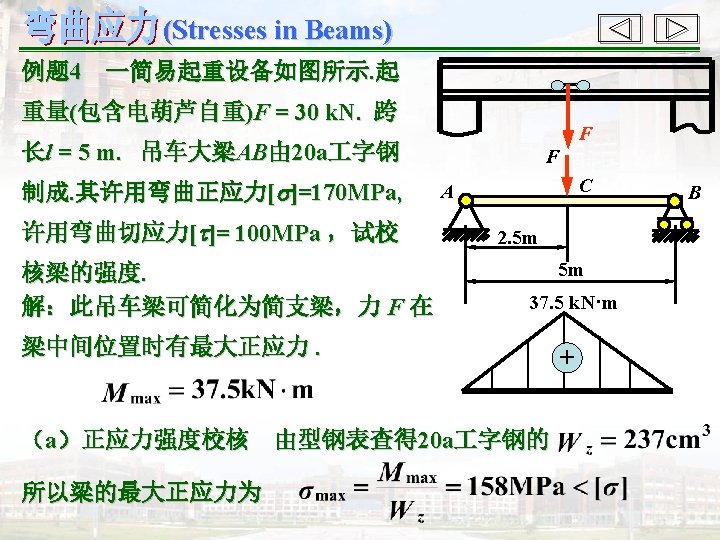

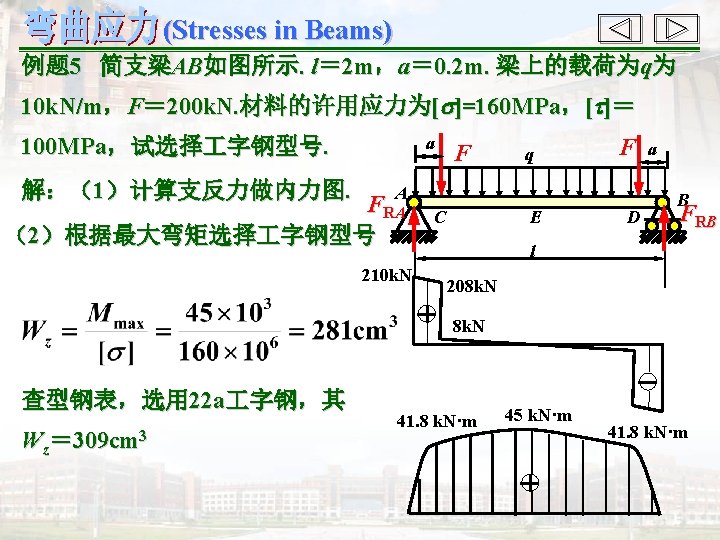


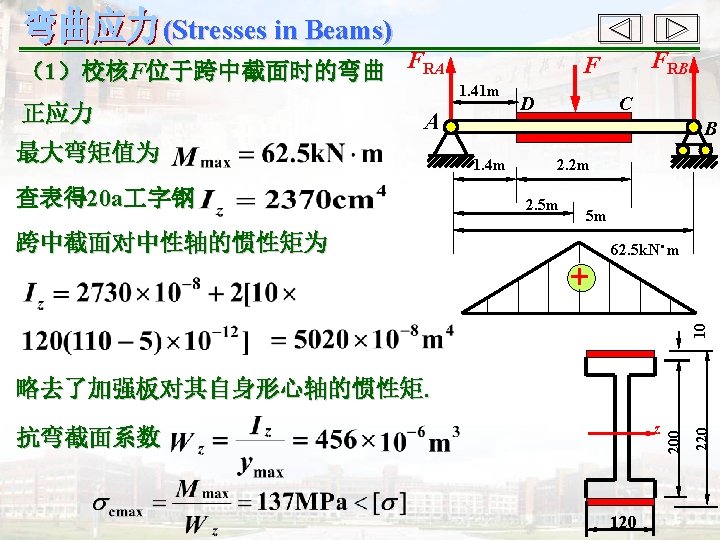






- Slides: 49