Chapter 5 Sources Shadows Shading Light source Anything




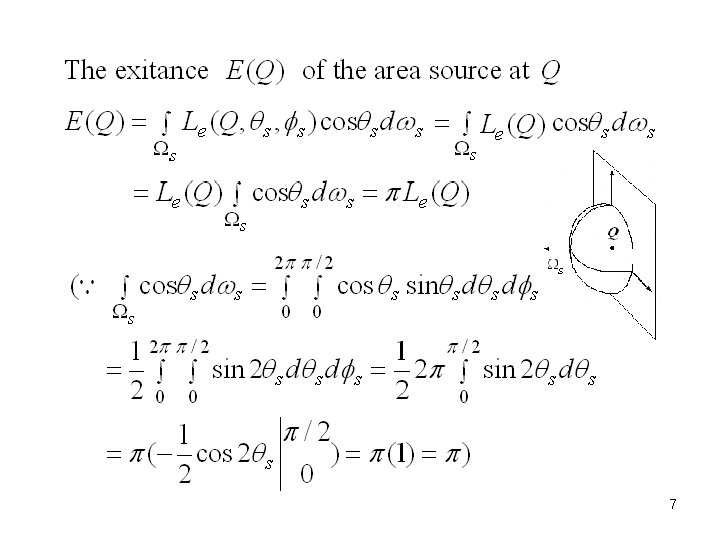








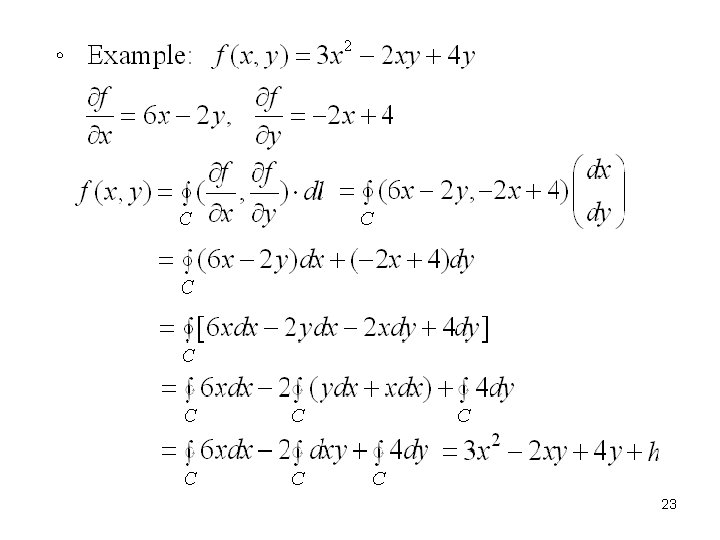





- Slides: 33

Chapter 5: Sources, Shadows, Shading Light source: Anything emits light that is internally generated Exitance: The internally generated power per unit area around a point 1

The geometry (e. g. , point, line, area) of the source has profound effects on the distribution of light around the source. 2

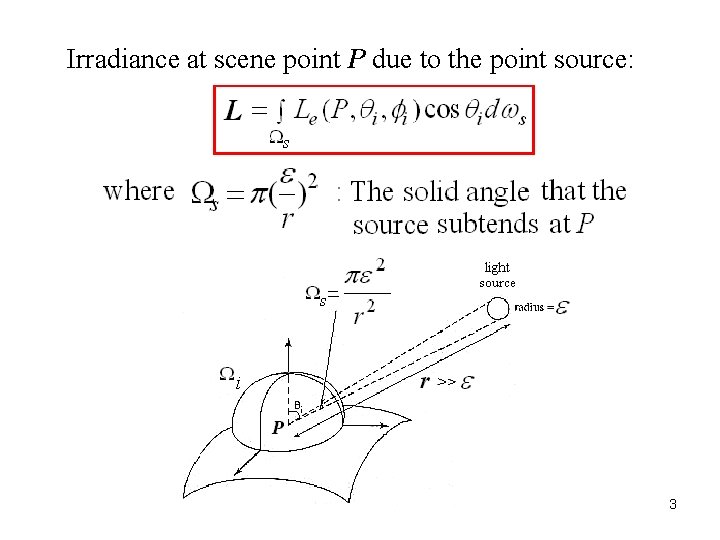
Irradiance at scene point P due to the point source: 3

4

5

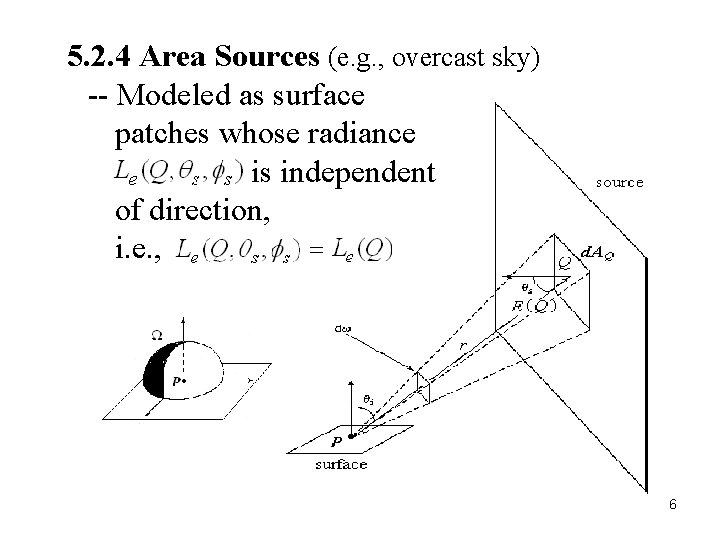
5. 2. 4 Area Sources (e. g. , overcast sky) -- Modeled as surface patches whose radiance is independent of direction, i. e. , 6
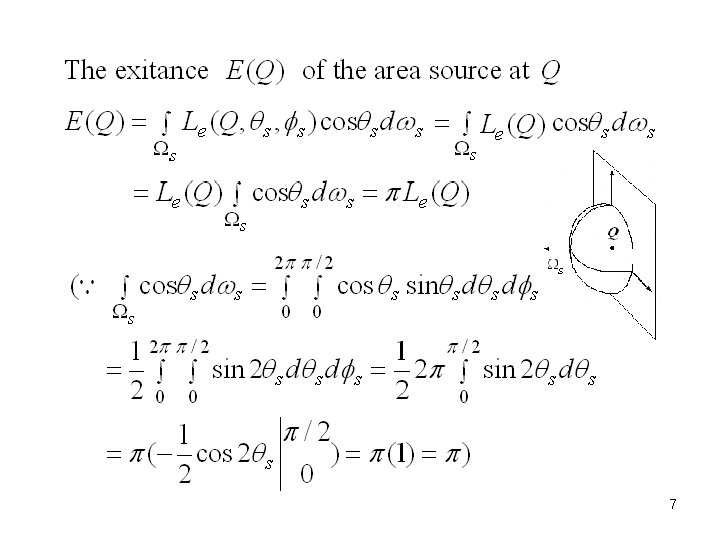
7

The radiosity at scene point P due to source point Q 8

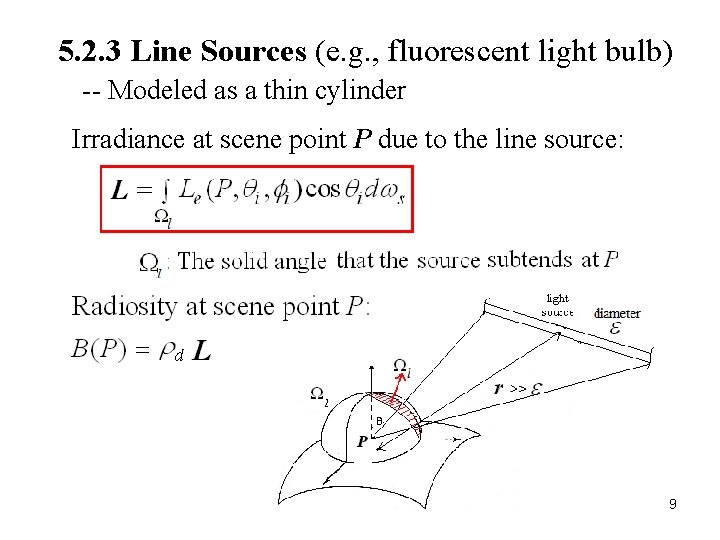
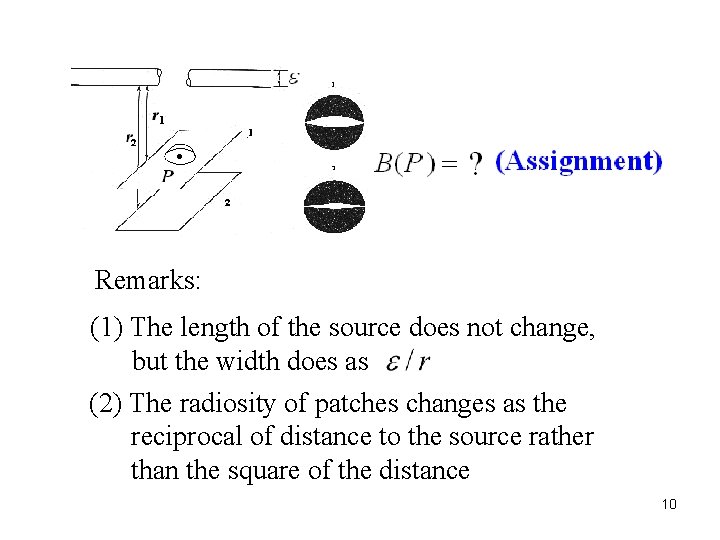
5. 2. 3 Line Sources (e. g. , fluorescent light bulb) -- Modeled as a thin cylinder Irradiance at scene point P due to the line source: 9

Remarks: (1) The length of the source does not change, but the width does as (2) The radiosity of patches changes as the reciprocal of distance to the source rather than the square of the distance 10

5. 3 Local Shading Model -- Describes radiosity at a scene point due to light sources Object Mesh Model Shaded Model 11

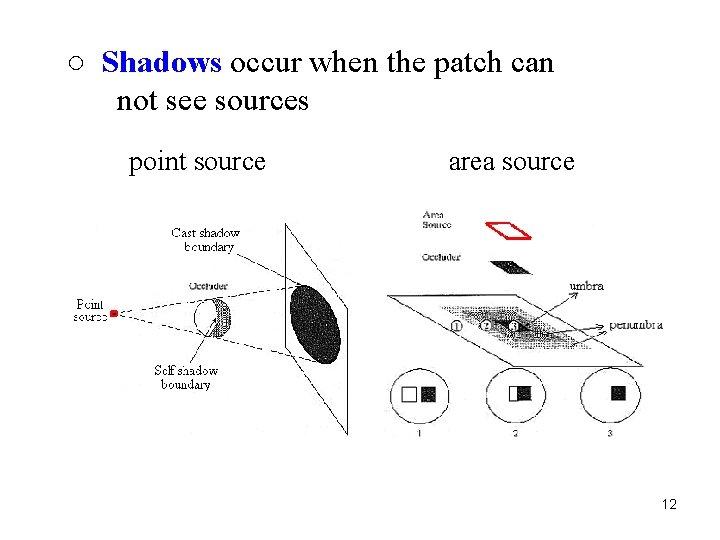
○ Shadows occur when the patch can not see sources point source area source 12

13

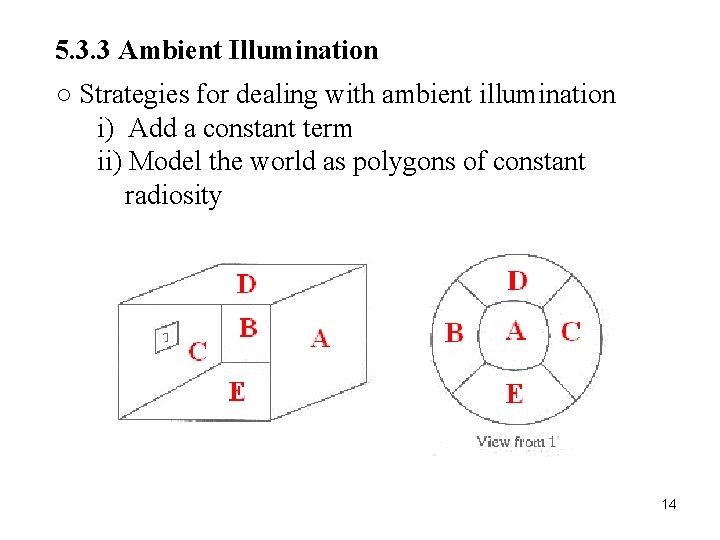
5. 3. 3 Ambient Illumination ○ Strategies for dealing with ambient illumination i) Add a constant term ii) Model the world as polygons of constant radiosity 14

5. 4 Application: Photometric Stereo -- Determines depths of pixels from a number of images taken under different illuminations. The variations in brightness code the shapes of scene surfaces 。 Example: Basketball 15

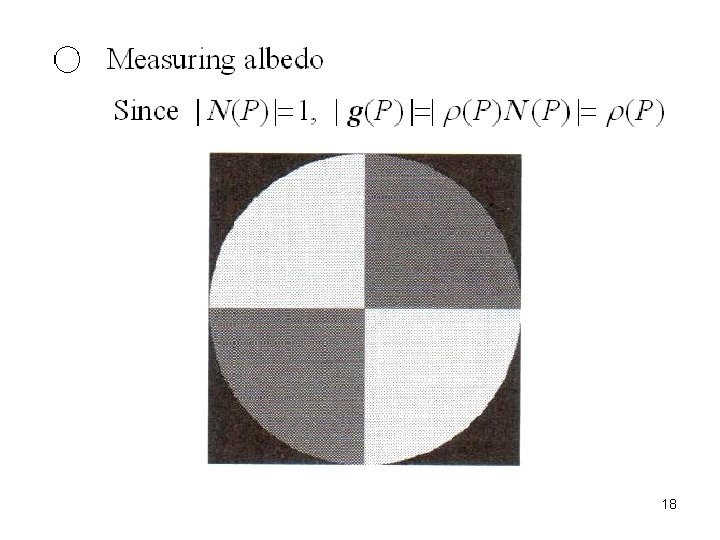
16

17

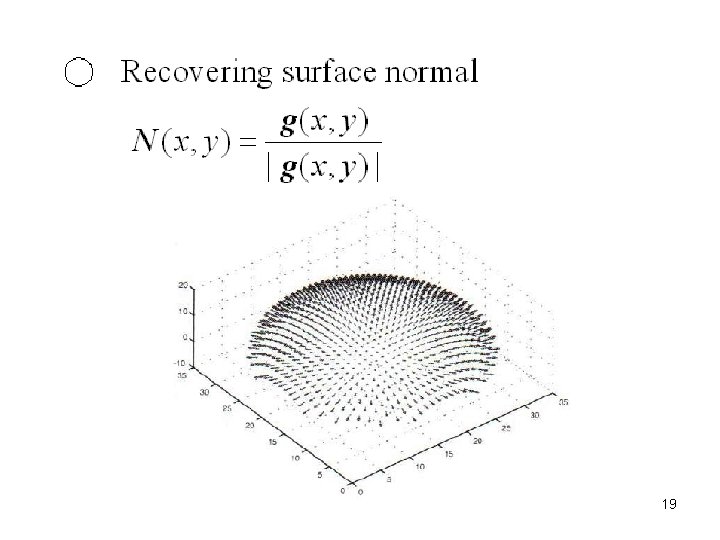
18

19

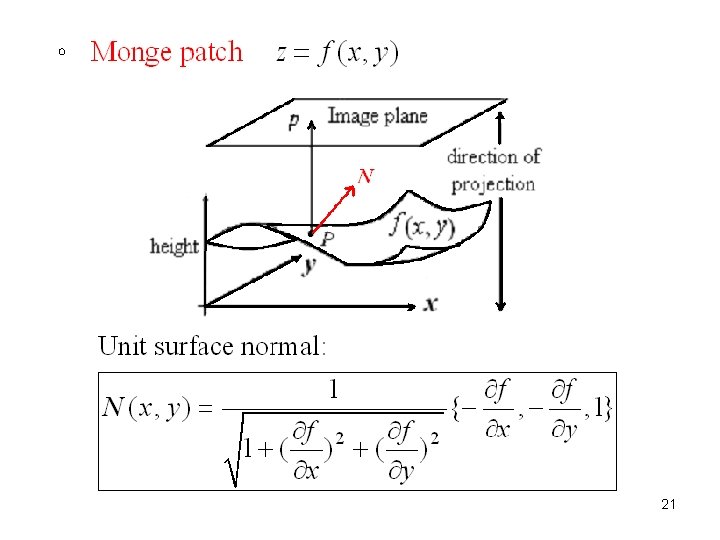
。 Monge curve -- A 2 D curve can be formulated by an explicit function, i. e. , 20

21

Derivatives give changes in surface height Reconstructing the surface by summing derivatives along some path C where C: ending at h: representing the height of the surface at the start point 22
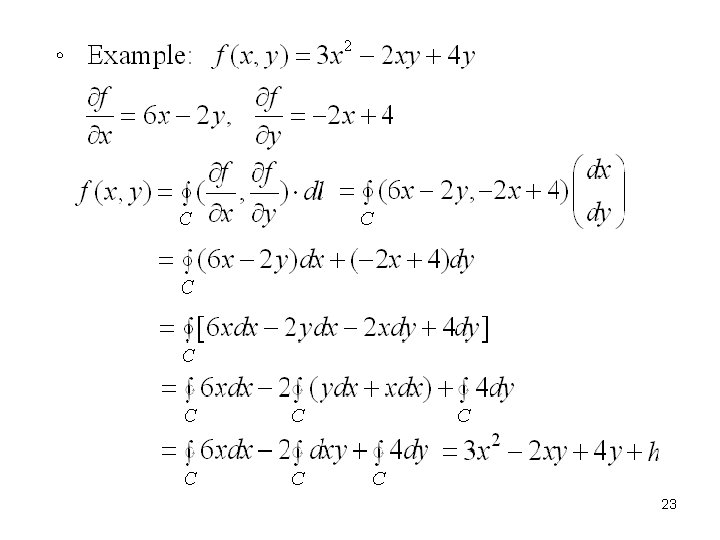
23

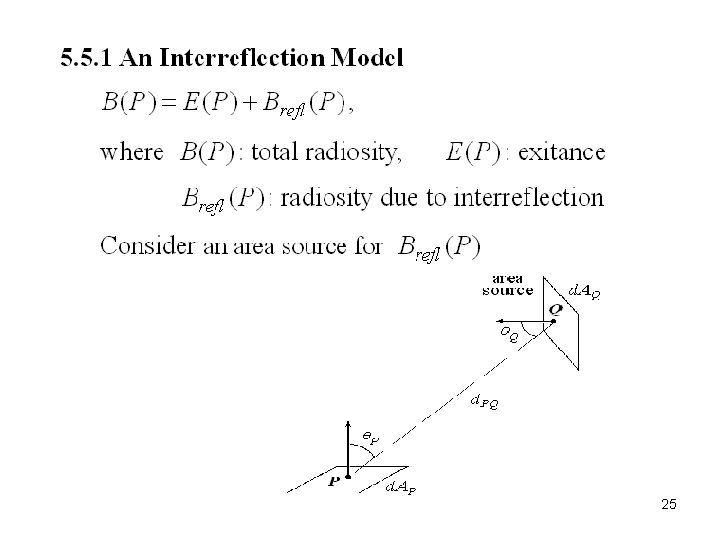
5. 5 Interreflections, Global Shading Models Interreflection: A surface patch is illuminated by light reflected off other patches Global Shading Model: A shading model incorporates interreflection effects 24

25

26

5. 5. 2 Solving for Radiosity Subdivide the world into small, flat patches with constant radiosity The radiosity at P on patch i due to the radiosity of patch j is 27

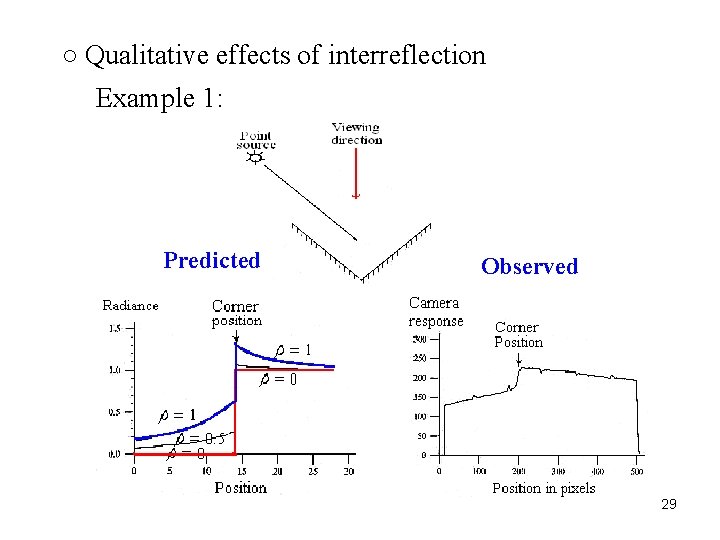
The total radiosity at P on patch i is 5. 5. 3 Qualitative Effects of Interreflections Local shading model describes the world poorly Global shading model involves unknown terms 28

○ Qualitative effects of interreflection Example 1: Predicted Observed 29

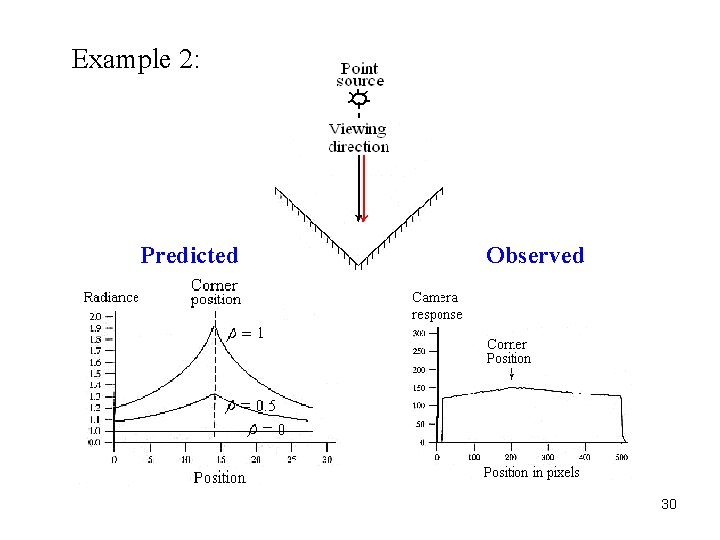
Example 2: Predicted Observed 30

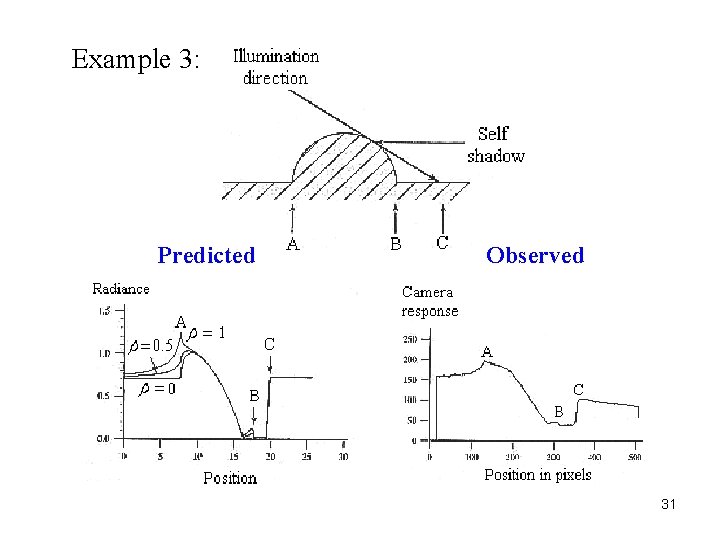
Example 3: Predicted Observed 31

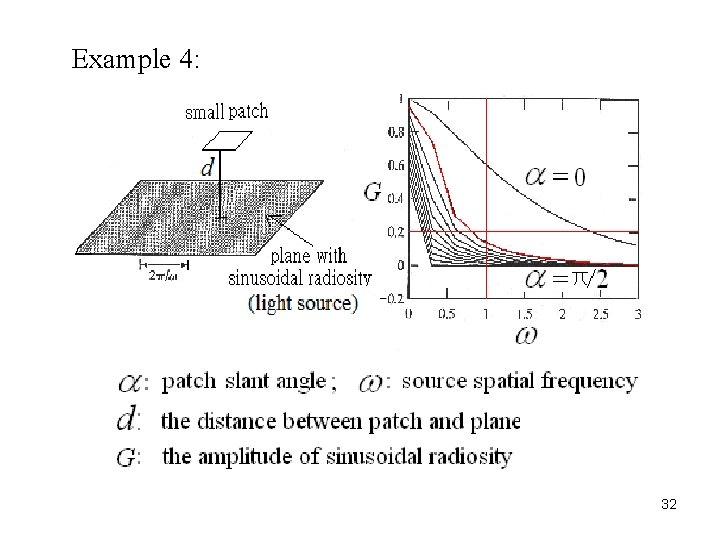
Example 4: 32

33