Chapter 5 Simple Applications of Macroscopic Thermodynamics Preliminary

Preliminary Discussion Classical, Macroscopic, Thermodynamics • For now, we drop the statistical mechanics notation

The “Calculus” of Thermodynamics Overview • The main focus of this chapter is The

• Another major objective of this chapter is to introduce techniques for recasting

Some Thermodynamic Variables: Internal Energy = E, Entropy = S Temperature = T •

• Assume that the External Parameter = Volume V in order to have

Combined st 1 & nd 2 Laws Td. S = d. E + pd.

Combined 1 st & 2 nd Laws: Td. S = d. E + pd.

A Brief, Pure Math Discussion!! • Consider 3 variables: x, y, z. Suppose that

• Suppose that, for these 3 variables: x, y, z, we take y

• The total differential of x(y, z) is: dx (∂x/∂y)zdy + (∂x/∂z)ydz (b)

• Consider again the 3 variables: x, y, z, & take x &

Mathematics Summary • Consider a function of 2 independent variables: f = f(x 1,

• Most Ch. 5 applications use this with the st nd Combined 1

Some Methods & Useful Math Tools for Transforming Derivatives Derivative Inversion Triple Product (xyz–

Pure Math: Jacobian Transformations • A Jacobian Transformation is often used to transform from

Jacobian Transformations Have Several Useful Properties Transposition Inversion Chain Rule Expansion

• Suppose that we are only interested in the first partial derivative of

Properties of the Internal Energy E d. E = Td. S – pd. V

Internal Energy E(S, V) S, V are independent variables: • We just showed that

• Instead of (S, V), if (S, p) are taken as independent variables,

• From the previous slide, the combined 1 st & 2 nd Laws

• Instead of (S, V), or (S, p), if (T, V) are taken

• If T & p are chosen as independent variables, it is convenient

Summary: Energy Functions 1. Internal Energy: E E(S, V) 2. Enthalpy: H = H(S,

Another Summary: Maxwell’s Relations (a) ΔE = Q + W (b) ΔS = (Qres/T)

Summary The 4 Most Common Maxwell Relations:

Maxwell Relations from d. E, d. F, d. H, & d. G Internal Energy

Slides: 50

Download presentation

Chapter 5: Simple Applications of Macroscopic Thermodynamics

Preliminary Discussion Classical, Macroscopic, Thermodynamics • For now, we drop the statistical mechanics notation for average quantities. So that now, All Variables are Averages Only! • We’ll discuss relationships between macroscopic variables using The Laws of Thermodynamics

The “Calculus” of Thermodynamics Overview • The main focus of this chapter is The development of functional property relationships for simple systems The relationships developed will be completely general. • These relationships are not physical property models. Instead, they represent practical constitutive equations specific for each pure substance or mixture.

• Another major objective of this chapter is to introduce techniques for recasting derived properties and their derivatives into forms that can be directly evaluated in terms of primitive properties which are measurable. • This objective will be accomplished by manipulating the st nd Combined 1 & 2 Laws through various differential calculus techniques

Some Thermodynamic Variables: Internal Energy = E, Entropy = S Temperature = T • Mostly for Gases: (also true for any substance): External Parameter = V Generalized Force = p (V = volume, p = pressure) • For a General System: External Parameter = x Generalized Force = X

• Assume that the External Parameter = Volume V in order to have a specific case to discuss. For systems with another external parameter x, the infinitesimal work done is đW = Xdx. In this case, in what follows, replace p by X & d. V by dx. • For infinitesimal, quasi-static processes: st 1 & nd 2 Laws of Thermodynamics 1 st Law: đQ = d. E + pd. V 2 nd Law: đQ = Td. S

Combined st 1 & nd 2 Laws Td. S = d. E + pd. V • Note that, in this relation, there are 5 Variables: T, S, E, p, V • It can be shown that: Any 3 of these can always be expressed as functions of any 2 others. • That is, there always 2 independent variables & 3 dependent variables. Which 2 are chosen as independent is arbitrary.

Combined 1 st & 2 nd Laws: Td. S = d. E + pd. V 5 Variables: T, S, E, p, V Any 3 of these can be expressed as functions of any 2 others.

Combined 1 st & 2 nd Laws: Td. S = d. E + pd. V 5 Variables: T, S, E, p, V Any 3 of these can be expressed as functions of any 2 others. • Always 2 independent variables & 3 dependent variables. Which 2 are chosen as independent is arbitrary. • The number N of possible choices of the 2 independent variables out of the 5 is N = (5!)/[(2!)(3!)] = 10 • In what follows, we discuss the 4 most common (& useful!) choices of the 2 independent variables.

A Brief, Pure Math Discussion!! • Consider 3 variables: x, y, z. Suppose that we know that x & y are Independent Variables. Then, It Must Be Possible to express z as a function of x & y. That is, There Must Exist a Function: z z(x, y).

• Suppose that, for these 3 variables: x, y, z, we take y & z as independent variables instead of x & y. Then, There Must be a Function x = x(y, z).

• Suppose that, for these 3 variables: x, y, z, we take y & z as independent variables instead of x & y. Then, There Must be a Function x = x(y, z). • From calculus, the total differential of x(y, z) is: dx (∂x/∂y)zdy + (∂x/∂z)ydz (b) • (a) from the previous slide is: dz (∂z/∂x)ydx + (∂z/∂y)xdy (a) • Using (a) & (b) together, the partial derivatives in (a) & those in (b) can be related to each other as follows:

• The total differential of x(y, z) is: dx (∂x/∂y)zdy + (∂x/∂z)ydz (b) • The total differential of z(x, y) is: dz (∂z/∂x)ydx + (∂z/∂y)xdy (a)

• The total differential of x(y, z) is: dx (∂x/∂y)zdy + (∂x/∂z)ydz (b) • The total differential of z(x, y) is: dz (∂z/∂x)ydx + (∂z/∂y)xdy (a) • Using (a) & (b) together, the partial derivatives in (a) & those in (b) can be related to each other as follows: • Suppose we are in a situation where z is constant. In that case, (a) becomes: 0 (∂z/∂x)ydx + (∂z/∂y)xdy (a') • Solve (a') for the ratio (dx/dy): (dx/dy) = - (∂z/∂y)x/(∂z/∂x)y (c)

• Consider again the 3 variables: x, y, z, & take x & y as independent variables. Then there Must be a Function z = z(x, y)

• Consider again the 3 variables: x, y, z, & take x & y as independent variables. Then there Must be a Function z = z(x, y) • The total differential of z is given by: dz (∂z/∂x)ydx + (∂z/∂y)xdy • In what follows, we always assume that all functions are analytic. So, the 2 nd cross derivatives are equal, such as: (∂2 z/∂x∂y) (∂2 z/∂y∂x), etc. • In what follows we’ll repeatedly use this property.

Mathematics Summary • Consider a function of 2 independent variables: f = f(x 1, x 2). • It’s exact differential is df y 1 dx 1 + y 2 dx 2 & by definition: • Because f(x 1, x 2) is an analytic function, it is always true that: 2 Or: [∂ (y 2)/∂x 1∂x 2)] 2 [∂ (y 1)/∂x 2∂x 1)]

• Most Ch. 5 applications use this with the st nd Combined 1 & 2 Laws of Thermodynamics Td. S = d. E + pd. V

Some Methods & Useful Math Tools for Transforming Derivatives Derivative Inversion Triple Product (xyz– 1 rule) Chain Rule Expansion to Add Another Variable Maxwell Reciprocity Relationship

Pure Math: Jacobian Transformations • A Jacobian Transformation is often used to transform from one set of independent variables to another. • For functions of 2 variables f(x, y) & g(x, y) it is: Determinant!

Jacobian Transformations Have Several Useful Properties Transposition Inversion Chain Rule Expansion

• Suppose that we are only interested in the first partial derivative of a function f(z, g) with respect to z at constant g: • This expression can be simplified using the chain rule expansion & the inversion property

Properties of the Internal Energy E d. E = Td. S – pd. V (1)

Properties of the Internal Energy E d. E = Td. S – pd. V (1) • First, choose S, V as independent variables: E E(S, V), so d. E ∂E ∂E (2)

Properties of the Internal Energy E d. E = Td. S – pd. V (1) • First, choose S, V as independent variables: E E(S, V), so d. E ∂E ∂E (2) • Comparison of (1) & (2) clearly shows that ∂E and ∂E

Internal Energy E(S, V) S, V are independent variables: • We just showed that ∂E ∂E (3)

Internal Energy E(S, V) S, V are independent variables: • We just showed that ∂E ∂E (3) • The general result for analytic functions is that the 2 nd cross derivatives are equal: So: (∂2 E/∂S∂V) (∂2 E/∂V∂S) (4)

• Instead of (S, V), if (S, p) are taken as independent variables, its useful to define the following energy: H H(S, p) E + p. V Enthalpy

• Instead of (S, V), if (S, p) are taken as independent variables, its useful to define the following energy: H H(S, p) E + p. V Enthalpy • Use the combined 1 st & 2 nd Laws. Rewrite them in terms of d. H: d. E = Td. S – pd. V = Td. S – [d(p. V) – Vdp] or d. H = Td. S + Vdp (1)

• From the previous slide, the combined 1 st & 2 nd Laws in terms of differential enthalpy d. H are: d. H = Td. S + Vdp • But, also: (1) (2)

• From the previous slide, the combined 1 st & 2 nd Laws in terms of differential enthalpy d. H are: d. H = Td. S + Vdp (1) (2) • But, also: • Comparison of (1) & (2) clearly shows that and

• From the previous slide, the combined 1 st & 2 nd Laws in terms of differential enthalpy d. H are: d. H = Td. S + Vdp (1) (2) • But, also: • Comparison of (1) & (2) clearly shows that and • Applying the general result for the 2 nd cross derivatives: Maxwell Relation II!

• Instead of (S, V), or (S, p), if (T, V) are taken as independent variables, its useful to define the energy: F F(T, V) E – TS Helmholtz Free Energy • Use the combined 1 st & 2 nd Laws. Rewrite them in terms of d. F: d. E = Td. S – pd. V = [d(TS) – Sd. T] – pd. V or d. F = -Sd. T – pd. V (1) • But, also: d. F ≡ ( F/ T)Vd. T + ( F/ V)Td. V (2)

• From the previous slide, the combined 1 st & 2 nd Laws in terms of differential Helmholtz free energy d. F are: d. F = -Sd. T – pd. V (1) • But, also: d. F ≡ ( F/ T)Vd. T + ( F/ V)Td. V (2) • Comparison of (1) & (2) clearly shows that ( F/ T)V ≡ -S and ( F/ V)T ≡ -p • Applying the general result for the 2 nd cross derivatives: Maxwell Relation III!

• If T & p are chosen as independent variables, it is convenient to define the energy: G G(T, p) E –TS + p. V Gibbs Free Energy • Use the combined 1 st & 2 nd Laws. Rewrite them in terms of d. G: d. E = Td. S – pd. V = d(TS) - Sd. T – [d(p. V) – Vdp] or d. G • But, also: = -Sd. T + Vdp (1) d. G ≡ ( G/ T)pd. T + ( G/ p)Tdp (2)

• From the previous slide, the combined 1 st & 2 nd Laws in terms of differential Gibbs free energy d. G are: d. G = -Sd. T + Vdp (1) • But, also: d. G ≡ ( G/ T)pd. T + ( G/ p)Tdp (2) • Comparison of (1) & (2) clearly shows that ( G/ T)p ≡ -S and ( G/ p)T ≡ V • Applying the general result for the 2 nd cross derivatives: Maxwell Relation IV!

Summary: Energy Functions 1. Internal Energy: E E(S, V) 2. Enthalpy: H = H(S, p) E + p. V 3. Helmholtz Free Energy: F = F (T, V) E – TS 4. Gibbs Free Energy: G = G(T, p) E – TS + p. V st 1 Combined & 2 nd Laws 1. d. E = Td. S – pd. V 2. d. H = Td. S + Vdp 3. d. F = - Sd. T – pd. V 4. d. G = - Sd. T + Vdp

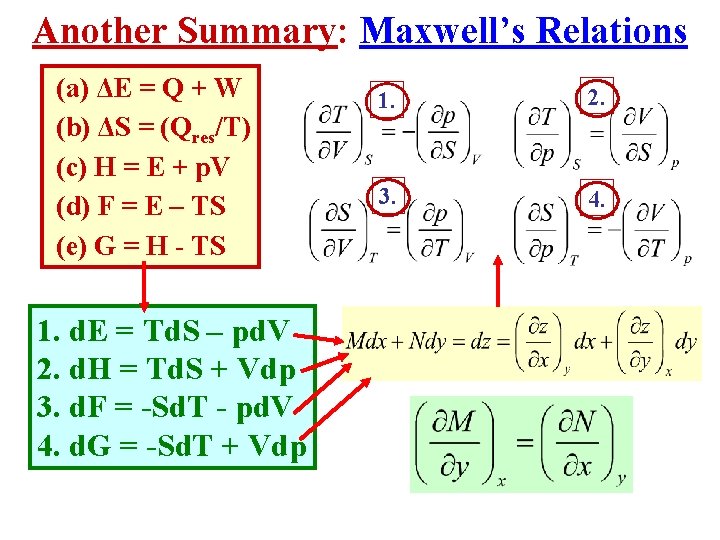
Another Summary: Maxwell’s Relations (a) ΔE = Q + W (b) ΔS = (Qres/T) (c) H = E + p. V (d) F = E – TS (e) G = H - TS 1. d. E = Td. S – pd. V 2. d. H = Td. S + Vdp 3. d. F = -Sd. T - pd. V 4. d. G = -Sd. T + Vdp 1. 2. 3. 4.

Summary The 4 Most Common Maxwell Relations:

Maxwell Relations: Table (E → U)

Maxwell Relations from d. E, d. F, d. H, & d. G Internal Energy Helmholtz Free Energy Enthalpy Gibbs Free Energy