Chapter 5 Section 5 5 Chapter 5 Normal

Chapter 5 Section 5 -5

Chapter 5 Normal Probability Distributions Section 5 -5 – Normal Approximations to Binomial Distributions 2. Correction for Continuity a. Binomial distributions only work for discrete data points. 1) When we want to calculate the exact binomial probabilities, we can find the probability of each value of x occurring and add them together. We did this in Chapter 4. b. To use a continuous normal distribution to approximate a binomial probability, you need to move. 5 unit to each side of the midpoint to include all possible x-values in the interval. 1) This is called making a correction for continuity. a) We simply subtract. 5 units from the lowest value and add. 5 units to the highest value. 3. There is a good review chart with this information displayed on page 288 of your text book.

Example 1 A (Page 286) Decide whether you can use the normal distribution to approximate x, the number of people who reply yes. If you can, find the mean and standard deviation. If you cannot, explain why. 51% of adults in the US who resolved to exercise more in the new year achieved their resolution. You randomly select 65 adults in the US whose resolution was to exercise more and ask each if he or she achieved their resolution. 15% of adults in the US do not make New Year’s resolutions. You randomly select 15 adults in the US and ask each if he or she made a New Year’s resolution.

Example 1 A (Page 286) Decide whether you can use the normal distribution to approximate x, the number of people who reply yes. If you can, find the mean and standard deviation. If you cannot, explain why. 51% of adults in the US who resolved to exercise more in the new year achieved their resolution. You randomly select 65 adults in the US whose resolution was to exercise more and ask each if he or she achieved their resolution. What are n, p and q? n = 65 p = 0. 51 q = 0. 49

Example 1 A (Page 286) 51% of adults in the US who resolved to exercise more in the new year achieved their resolution. You randomly select 65 adults in the US whose resolution was to exercise more and ask each if he or she achieved their resolution. n = 65 p = 0. 51 q = 0. 49 Are np and nq greater than or equal to 5? (65)(. 51) = 33. 15 and (65)(. 49) = 31. 85 Since both of these are greater than 5, we CAN use the normal distribution.

Example 1 B (Page 286) 15% of adults in the US do not make New Year’s resolutions. You randomly select 15 adults in the US and ask each if he or she made a New Year’s resolution. What are n, p and q? n = 15 p = 0. 15 q = 0. 85

Example 1 B (Page 286) 15% of adults in the US do not make New Year’s resolutions. You randomly select 15 adults in the US and ask each if he or she made a New Year’s resolution. n = 15 p = 0. 15 q = 0. 85 Are np and nq greater than or equal to 5? (15)(. 15) = 2. 25 and (15)(. 85) = 12. 75 Since np < 5, we CANNOT use the normal distribution to approximate the distribution of x.

Example 2 (Page 287) Use a correction for continuity to convert each of the following binomial intervals to a normal distribution interval. 1. The probability of getting between 270 and 310 successes, inclusive. 2. The probability of at least 158 successes. 3. The probability of getting less than 63 successes.

Example 2 (Page 287) Use a correction for continuity to convert each of the following binomial intervals to a normal distribution interval. 1. The probability of getting between 270 and 310 successes, inclusive. Since we are dealing with whole numbers, we subtract. 5 from the low end add. 5 to the high end. 270 -. 5 = 269. 5 310 +. 5 = 310. 5 Our interval is 269. 5 < x < 310. 5

Example 2 (Page 287) Use a correction for continuity to convert each of the following binomial intervals to a normal distribution interval. 2. The probability of at least 158 successes. Since 158 is the low end, our interval is x > 157. 5.

Example 2 (Page 287) Use a correction for continuity to convert each of the following binomial intervals to a normal distribution interval. 3. The probability of getting less than 63 successes. We want all numbers less than 63, which makes 62 the upper end. We add. 5 to the upper end to get x < 62. 5.

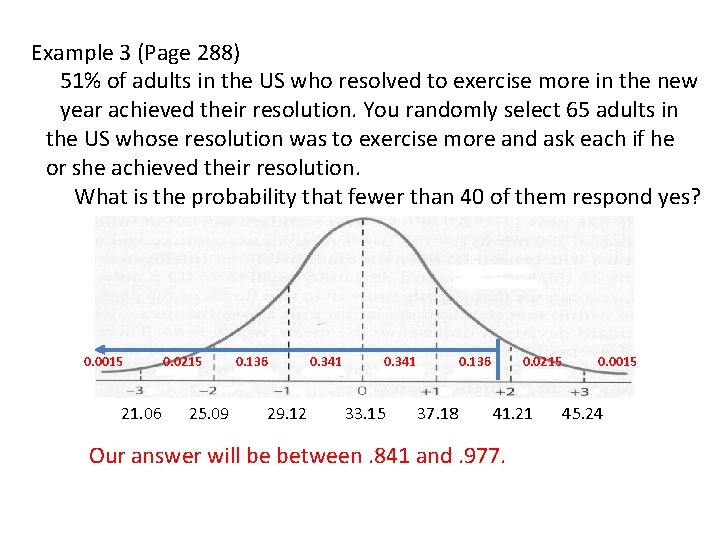
Example 3 (Page 288) 51% of adults in the US who resolved to exercise more in the new year achieved their resolution. You randomly select 65 adults in the US whose resolution was to exercise more and ask each if he or she achieved their resolution. What is the probability that fewer than 40 of them respond yes? We know from Example 1 A that we can use the normal distribution, with a mean of 33. 15 and a standard deviation of 4. 03 Correcting for continuity means that we use 39. 5, since 39 is the highest number less than 40, and it is at the high end of the interval.

Example 3 (Page 288) 51% of adults in the US who resolved to exercise more in the new year achieved their resolution. You randomly select 65 adults in the US whose resolution was to exercise more and ask each if he or she achieved their resolution. What is the probability that fewer than 40 of them respond yes? 0. 0015 21. 06 0. 0215 25. 09 0. 136 29. 12 0. 341 33. 15 0. 136 37. 18 0. 0215 41. 21 Our answer will be between. 841 and. 977. 0. 0015 45. 24

Example 3 (Page 288) 51% of adults in the US who resolved to exercise more in the new year achieved their resolution. You randomly select 65 adults in the US whose resolution was to exercise more and ask each if he or she achieved their resolution. What is the probability that fewer than 40 of them respond yes? 2 nd VARS 2 (-1 E 99, 39. 5, 33. 15, 4. 03) gives us. 942. This fits between. 841 and. 977. Also, 2 nd VARS 3 (. 942, 33. 2, 4. 03) = 39. 534, so it checks. We have a 94. 2% probability that fewer than 40 people will respond “Yes”.

0. 0015 0. 0215 55. 408 62. 272 0. 136 0. 341 69. 136 0. 341 76 0. 136 82. 864 0. 0215 89. 728 0. 0015 96. 592

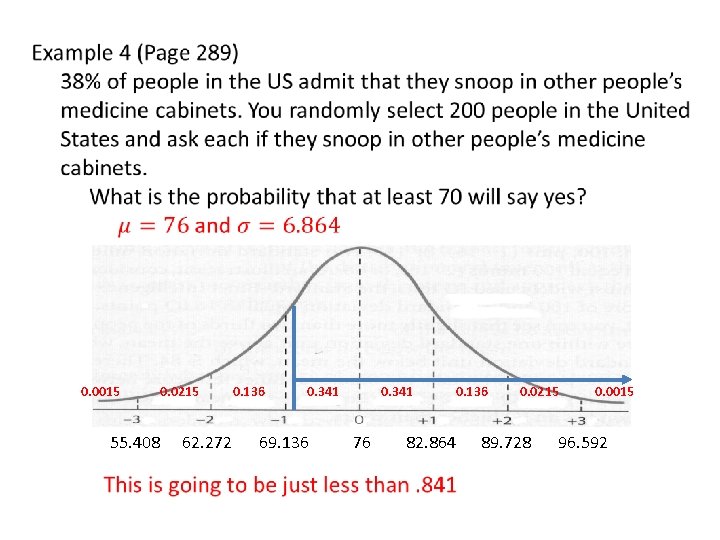
Example 4 (Page 289) 38% of people in the US admit that they snoop in other people’s medicine cabinets. You randomly select 200 people in the United States and ask each if they snoop in other people’s medicine cabinets. What is the probability that at least 70 will say yes? Correcting for continuity means that we subtract. 5 from 70 (the low end of the interval) to get 69. 5. 2 nd VARS 2 (69. 5, 1 E 99, 76, 6. 864) =. 8282 This matches our estimate of just less than. 841 2 nd VARS 3 (1 -. 8282, 76, 6. 864) = 69. 499 (it checks) We have an 82. 8% probability that at least 70 people will respond “Yes”.

Example 5 (Page 290) 1. A survey reports that 86% of internet users use Windows Internet Explorer as their browser. You randomly select 200 internet users and ask each whether he or she uses Internet Explorer as his or her browser. What is the probability that exactly 176 say yes? Alternatively, we can use the normalcdf to find the area between 175. 5 and 176. 5 (176 corrected for continuity). 2 nd VARS 2 (175. 5, 176. 5, 172, 4. 907) =. 0583 Either way, we have about a 5. 83% chance of getting exactly 176 out of 200 people to say that they use Internet Explorer as their browser.

YOUR ASSIGNMENTS ARE: Classwork: Page 291 #1 -16 All Homework: Page 292 -294 #19 -26 All