CHAPTER 5 SECTION 5 5 BASES OTHER THAN

CHAPTER 5 SECTION 5. 5 BASES OTHER THAN e AND APPLICATIONS

Definition of Exponential Function to Base a
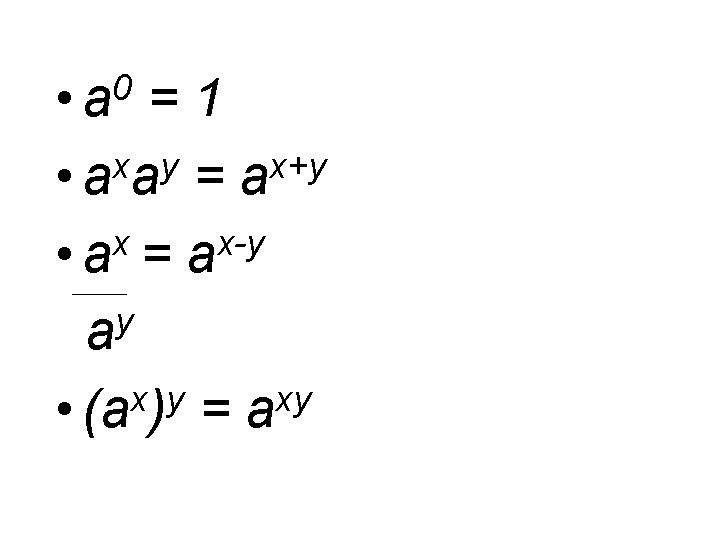
0 • a =1 x y x+y • a a = a x x-y • a = a y a x y xy • (a ) = a

Definition of Logarithmic Function to Base a
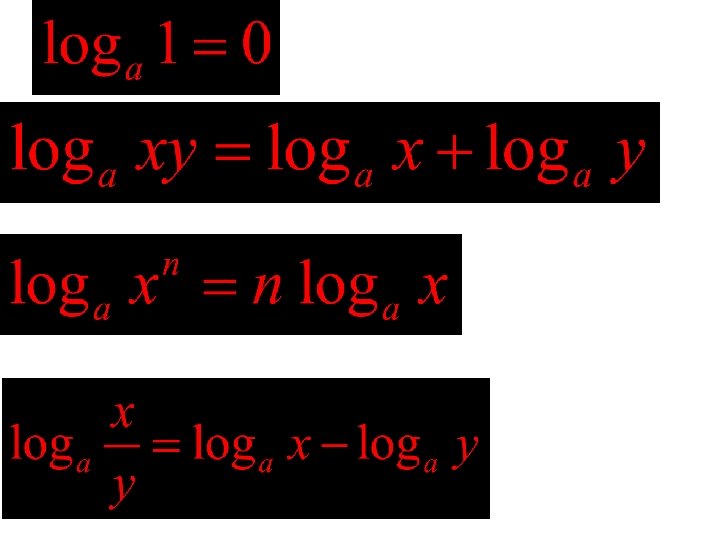

Properties of Inverse Functions
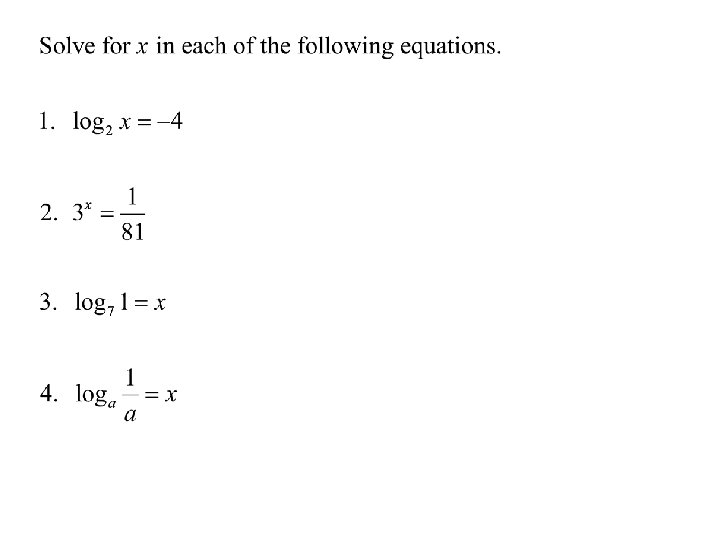
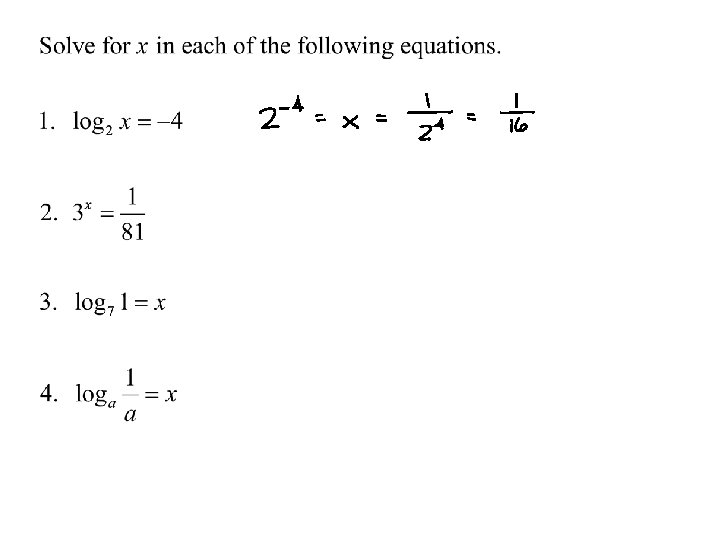
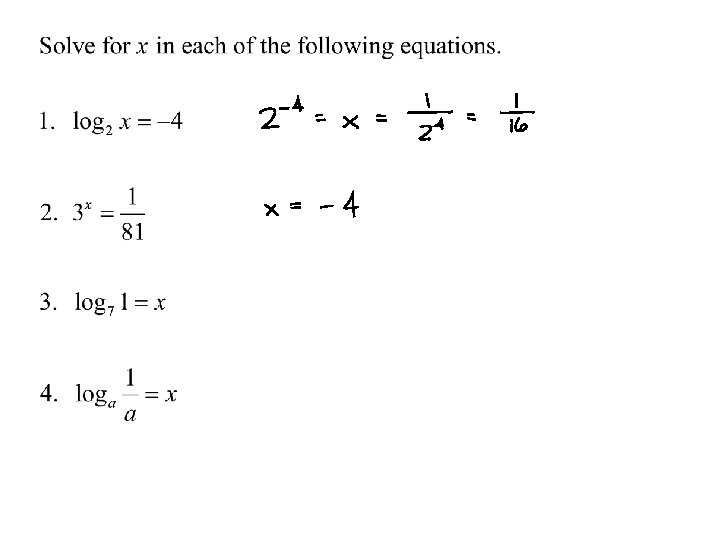
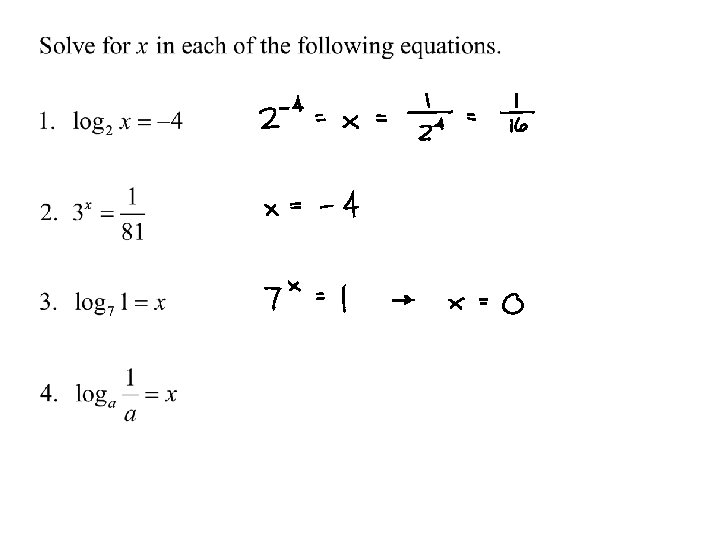
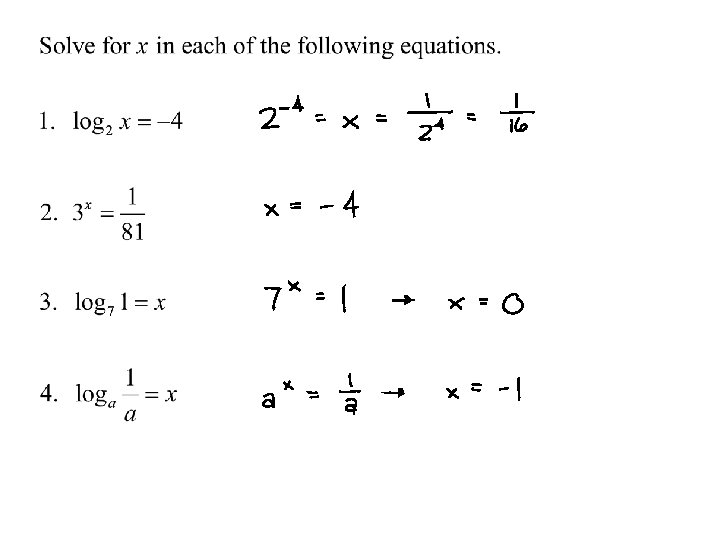

Theorem 5. 13 Derivatives for Bases Other Than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Examples for Derivatives for Bases other than e

Theorem 5. 14 The Power Rule for Real Exponents

Differentiate. Hint: Take the ln of both sides.

Find each derivative with respect to the given variable.
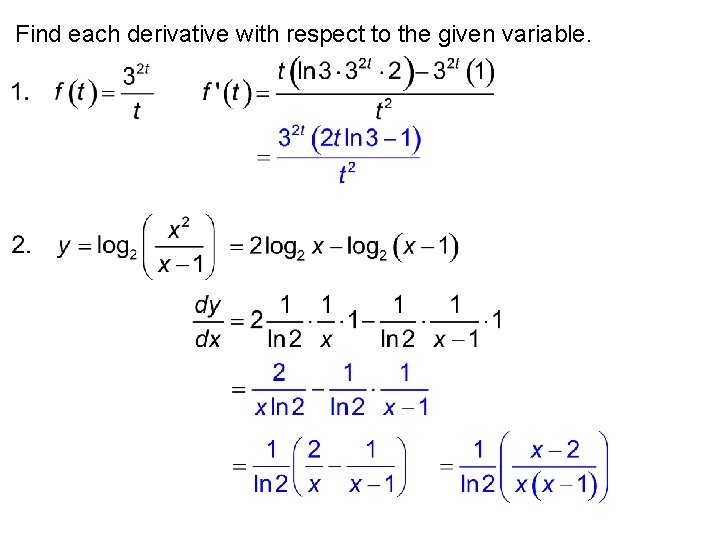
Find each derivative with respect to the given variable.

Find each derivative with respect to the given variable.

Find each derivative with respect to the given variable.

LOGARITHMIC DIFFERENTIATION • Differentiate . – Using logarithmic differentiation, we have:

To integrate exponential functions other than base e, either • Convert to base e using the formula Or q Integrate directly using the integration formula

EXP. FUNCTIONS WITH BASE a • Example 14

Theorem: Proof:
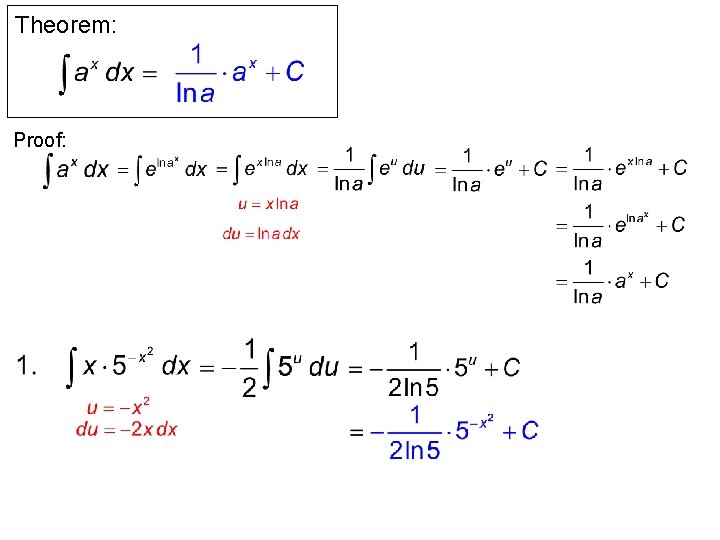
Theorem: Proof:

Theorem 5. 15 A Limit Involving e

Applications of Exponential Functions • Compound Interest Formulas – Compounded n times per year: – Compounded continuously: Where t = number of years, P = Initial deposit, A = balance after t years, r = interest rate expresses as a decimal, n = number of compounding periods per years.

A deposit of $2500 invested into an account paying an interest rate of 10%. Find its balance after 5 years if interest is compounded… a. quarterly b. monthly c. continuously

A deposit of $2500 invested into an account paying an interest rate of 10%. Find its balance after 5 years if interest is compounded… a. quarterly b. monthly c. continuously
- Slides: 39