Chapter 5 Section 5 1 Perpendiculars and Bisectors

Chapter 5 Section 5. 1 Perpendiculars and Bisectors

Vocabulary Perpendicular Bisector: A segment, ray, line, or plane that is perpendicular to a segment at its midpoint is called a perpendicular bisector Equidistant: Being the same distance away from two or more objects A point can be equidistant from two other points A point can be equidistant from two lines Distance from a point to a line: Defined to be the length of a segment through the point perpendicular to the line

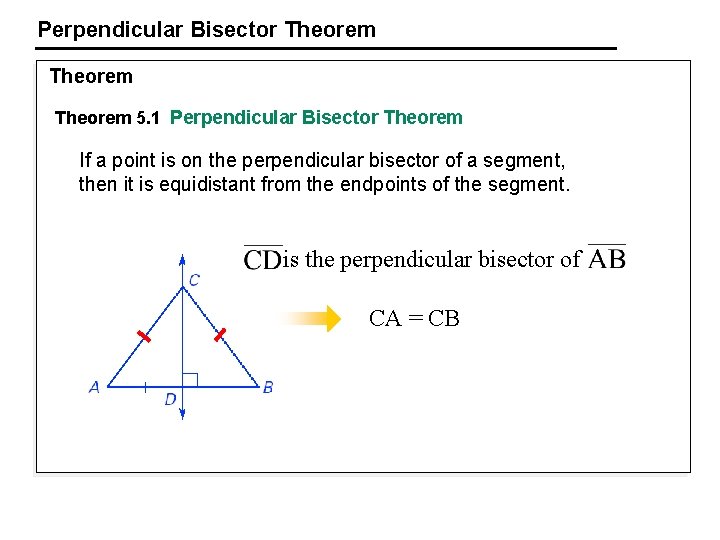
Perpendicular Bisector Theorem 5. 1 Perpendicular Bisector Theorem If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. is the perpendicular bisector of CA = CB

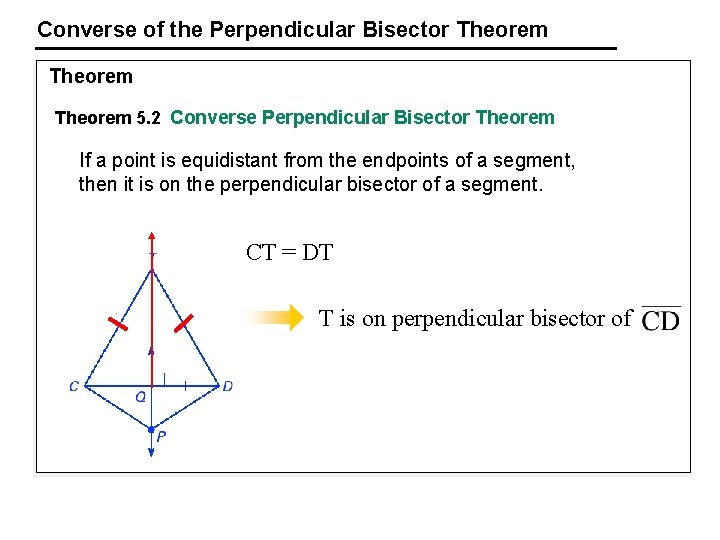
Converse of the Perpendicular Bisector Theorem 5. 2 Converse Perpendicular Bisector Theorem If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of a segment. CT = DT T is on perpendicular bisector of

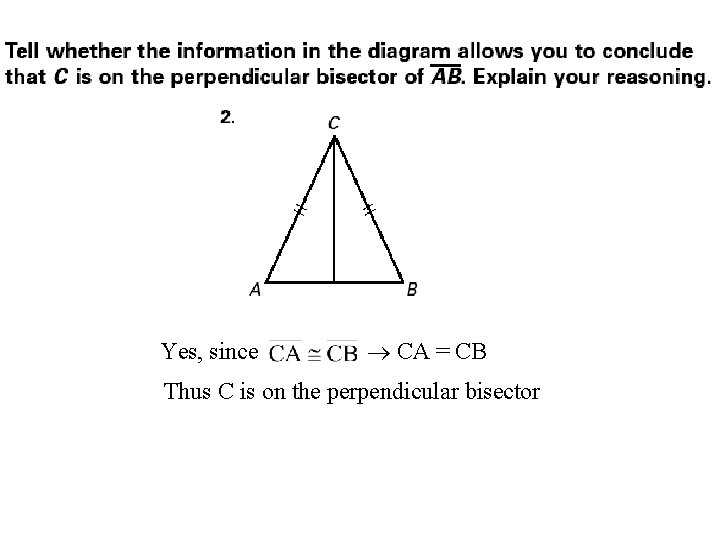
Yes, since CA = CB Thus C is on the perpendicular bisector

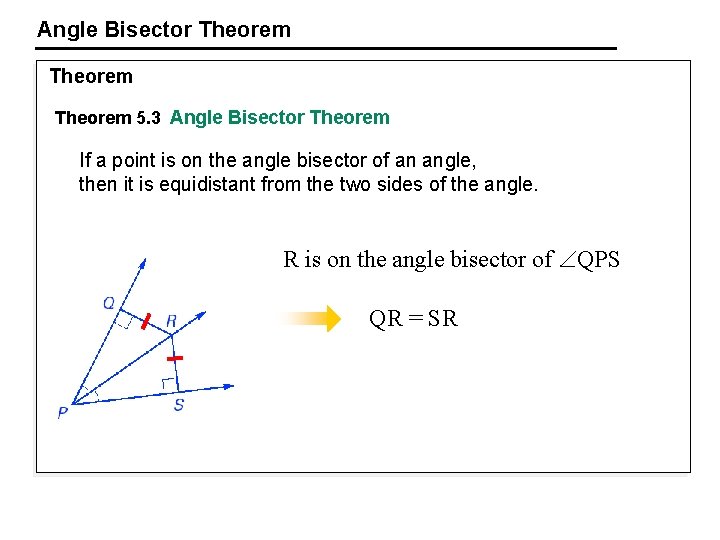
Angle Bisector Theorem 5. 3 Angle Bisector Theorem If a point is on the angle bisector of an angle, then it is equidistant from the two sides of the angle. R is on the angle bisector of QPS QR = SR

Converse of the Angle Bisector Theorem 5. 4 Converse Angle Bisector Theorem If a point is equidistant from the two sides of the angle, then it is on the angle bisector of an angle. QR = SR R is on angle bisector of QPS

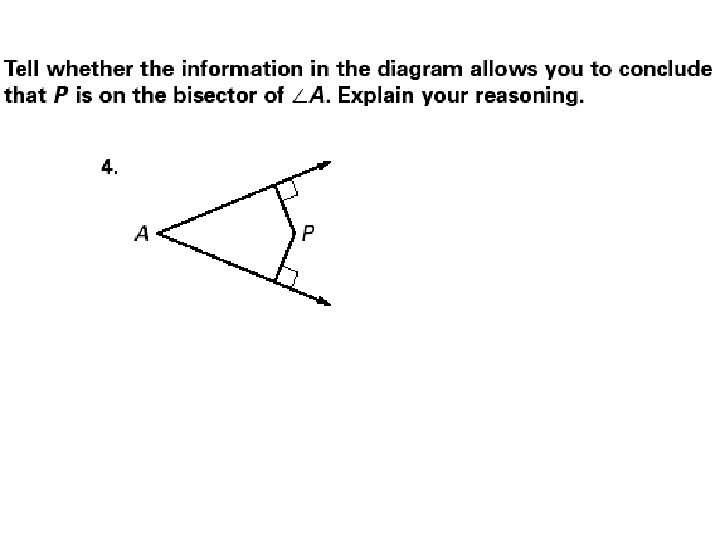
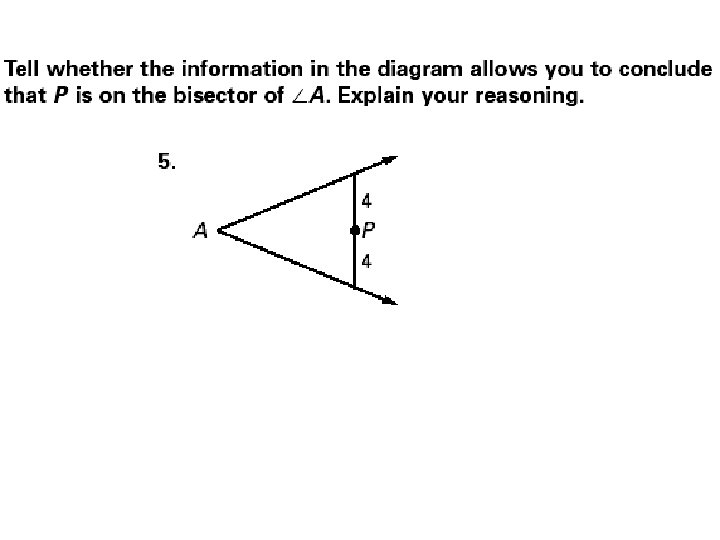
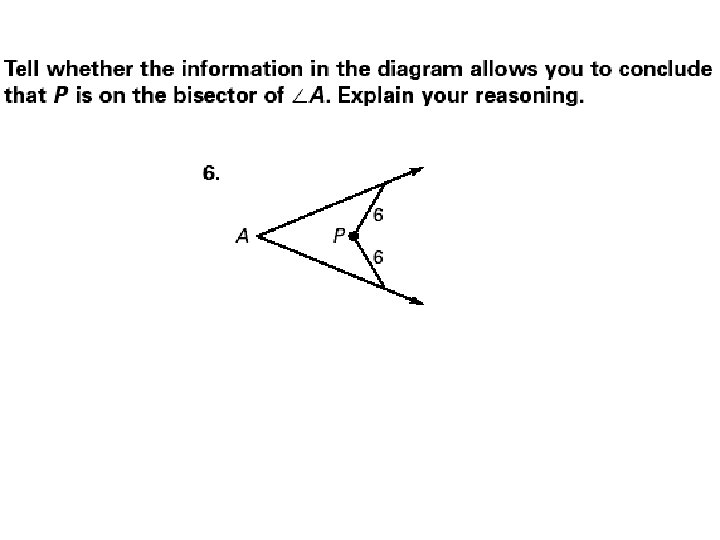
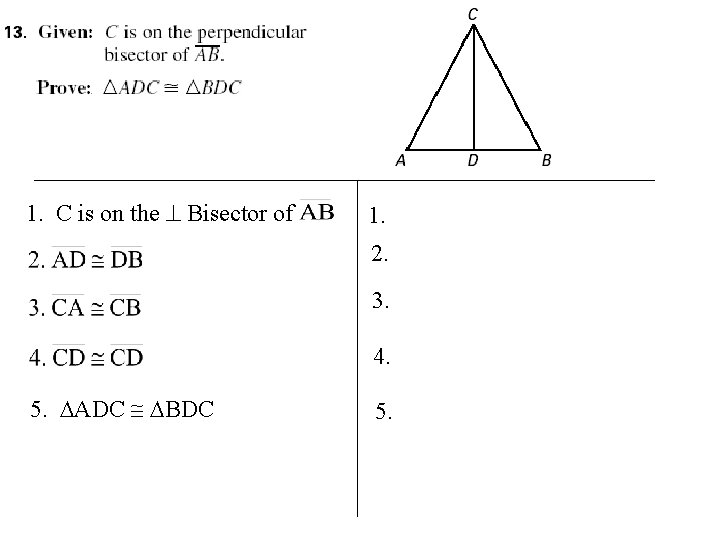
1. C is on the Bisector of 1. 2. 3. 4. 5. ADC BDC 5.

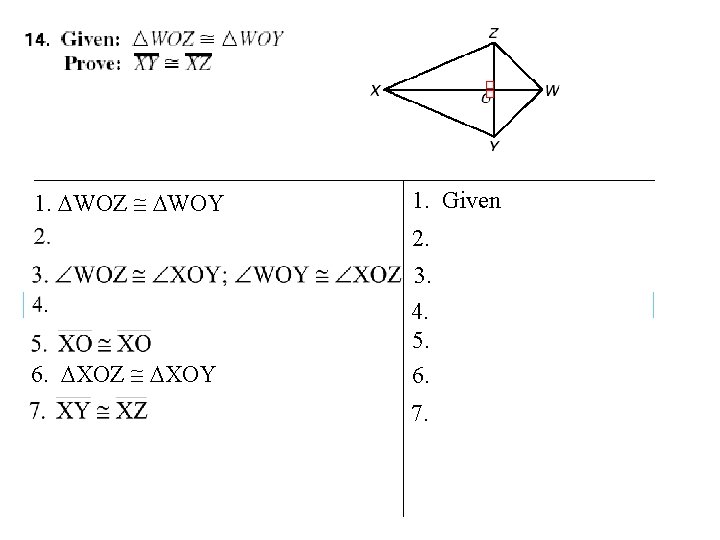
1. WOZ WOY 1. Given 2. 3. 6. XOZ XOY 4. 5. 6. 7.