Chapter 5 Section 1 Bisectors of Triangles Vocabulary

Chapter 5 Section 1 Bisectors of Triangles

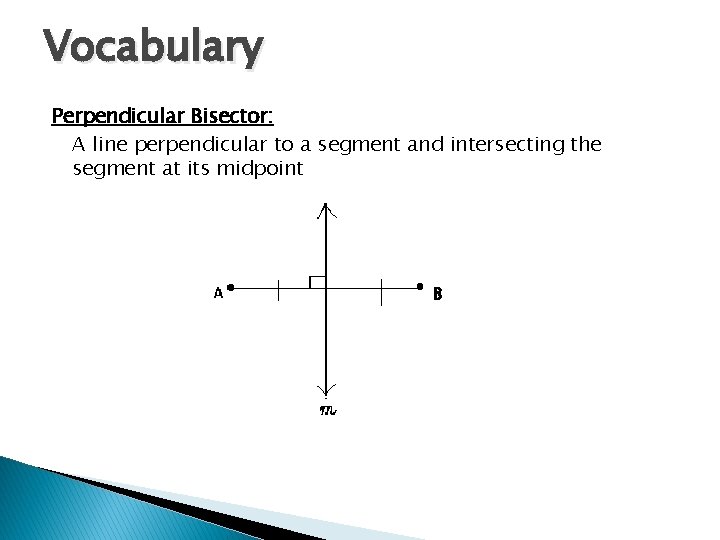
Vocabulary Perpendicular Bisector: A line perpendicular to a segment and intersecting the segment at its midpoint B

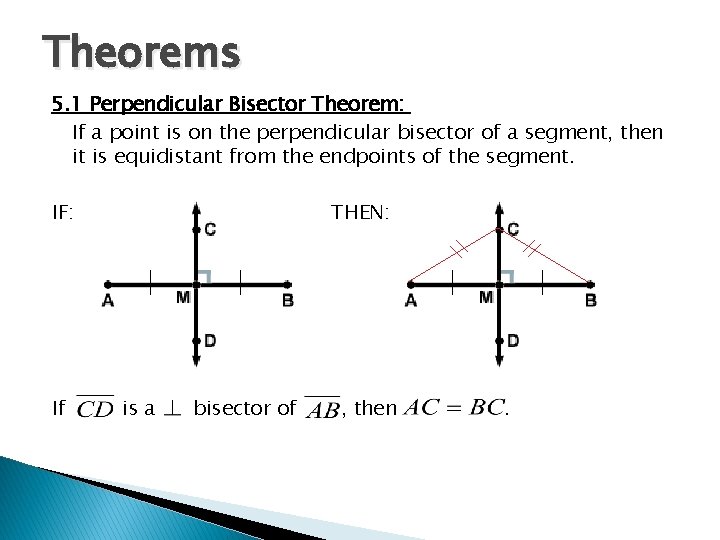
Theorems 5. 1 Perpendicular Bisector Theorem: If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. IF: If THEN: is a bisector of , then .

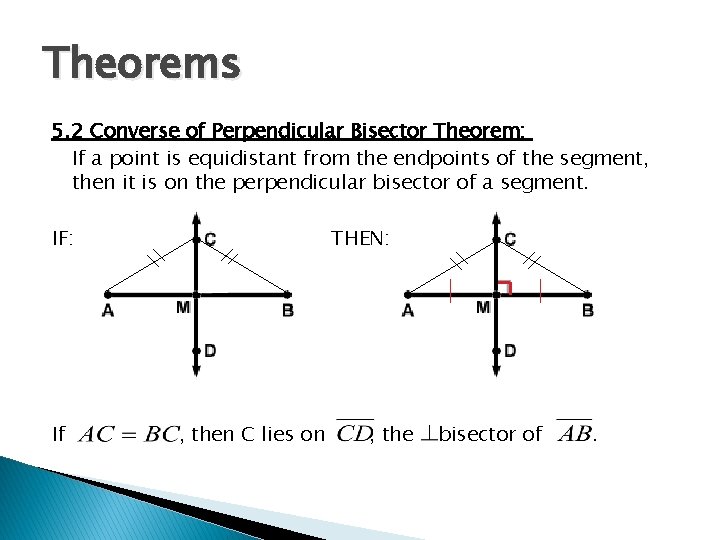
Theorems 5. 2 Converse of Perpendicular Bisector Theorem: If a point is equidistant from the endpoints of the segment, then it is on the perpendicular bisector of a segment. IF: If THEN: , then C lies on , the bisector of .

Vocabulary Concurrent Lines: Three or more lines intersecting at the same the point Point of Concurrency: Point where concurrent lines intersect Circumcenter: The point of concurrency of the three perpendicular bisectors of a triangle (See Circumcenter Theorem for picture)

Theorems 5. 3 Circumcenter Theorem: The perpendicular bisectors of a triangle intersect at a point called the circumcenter that is equidistant from the vertices of the triangle. If G is the circumcenter of then. ABC,

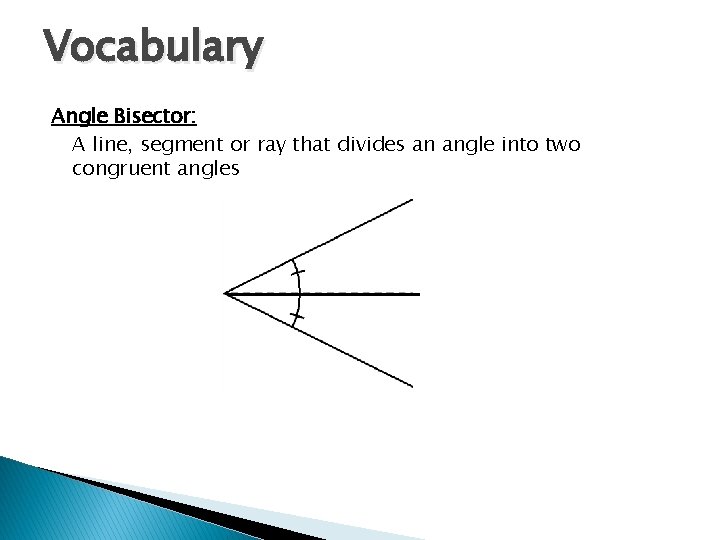
Vocabulary Angle Bisector: A line, segment or ray that divides an angle into two congruent angles

Theorems 5. 4 Angle Bisector Theorem: If a point is on the bisector of an angle, then it is equidistant from the sides of the angle. IF: THEN: D D F B If F B E bisects , and E then .

Theorems 5. 5 Converse of Angle Bisector Theorem: If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle. IF: THEN: D D F F B If B E , and then E bisects .

Vocabulary Incenter: The point of concurrency of the three angle bisectors of a triangle (See Incenter Theorem for picture)

Theorems 5. 6 Incenter Theorem: The angle bisectors of a triangle intersect at a point called the incenter that is equidistant from each side of the triangle. If G is the incenter of Then. ABC,