Chapter 5 Relationships in Triangles Lesson 5 1

Chapter 5: Relationships in Triangles

Lesson 5. 1 Bisectors, Medians, and Altitudes

Foldable n Frayer: Fold paper in half both width and length wise. While folded, fold the corner where all creases meet. Then open.

Perpendicular Bisector ( n A line, segment, or ray that passes through the midpoint of the side and is perpendicular to the side. n n bisector) Does not need to pass through a vertex Any point on a perpendicular bisector is equidistant from the endpoints Any point equidistant from the endpoints is on the perpendicular bisector Circumcenter: the point where 3 perpendicular bisectors meet n Is equidistant from all vertices of the triangle

Perpendicular Bisector A CF, BE, and AD are perpendicular bisectors OB, OC and OA are congruent F E O B There always 3 perpendicular bisectors for a triangle C D

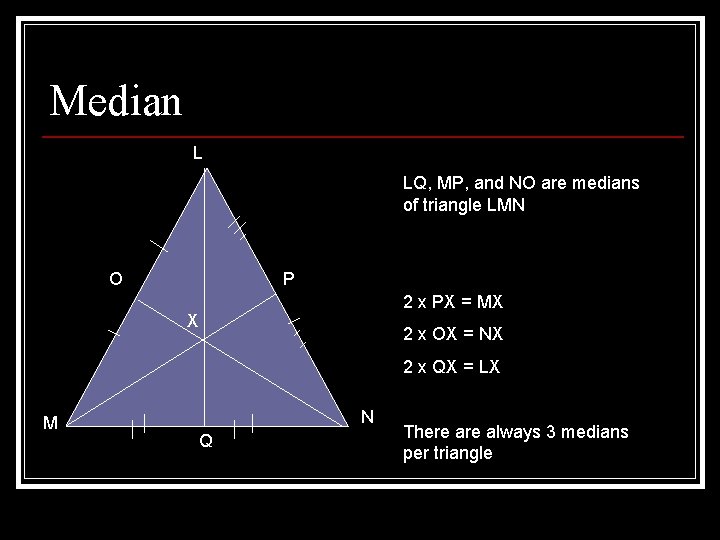
Median n n A segment that goes from a vertex of the triangle to the midpoint of the opposite side Centroid: is the point where three medians intersect n n The center of gravity for the triangle The small part of the median is 1/3 of the whole median n 2 x small = big 1/3 median = small 2/3 median = big

Median L LQ, MP, and NO are medians of triangle LMN O P 2 x PX = MX X 2 x OX = NX 2 x QX = LX M N Q There always 3 medians per triangle

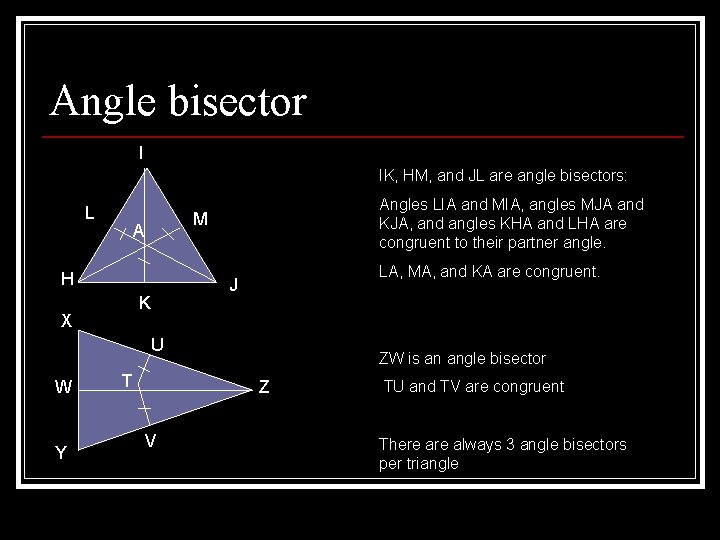
Angle Bisector ( n A line, segment or ray that passes through the middle of the angle it begins in and extends to the opposite side n n n bisector) Any point on the angle bisector is equidistant from the sides of the triangle Any point equidistant from both sides is on the angle bisector Incenter: the point where three angle bisectors intersect n Equidistant from all sides of the triangle

Angle bisector I IK, HM, and JL are angle bisectors: L M A H LA, MA, and KA are congruent. J K X Angles LIA and MIA, angles MJA and KJA, and angles KHA and LHA are congruent to their partner angle. U W Y T ZW is an angle bisector Z V TU and TV are congruent There always 3 angle bisectors per triangle

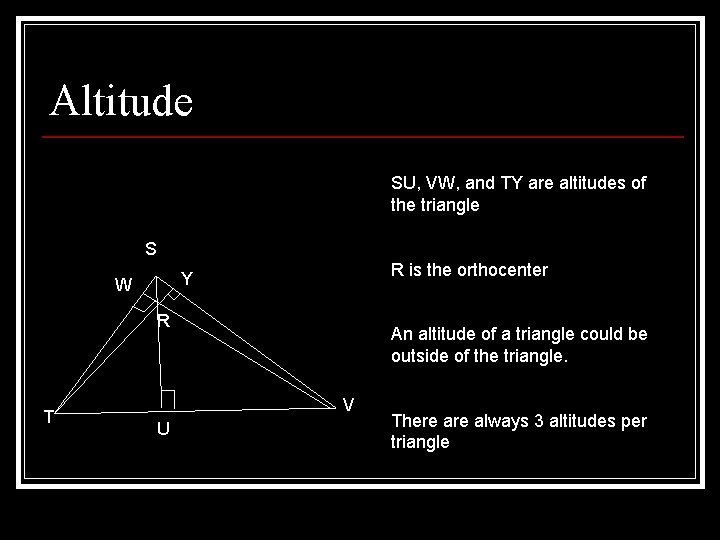
Altitude n A segment that goes from a vertex of the triangle to the opposite side and is perpendicular to that side n Orthocenter: the point where three altitudes intersect

Altitude SU, VW, and TY are altitudes of the triangle S R is the orthocenter Y W R T An altitude of a triangle could be outside of the triangle. V U There always 3 altitudes per triangle

Lesson 5. 2 Inequalities and Triangles

Foldable Fold the paper into three sections (burrito fold) Then fold the top edge down about ½ and inch n Unfold the paper and in the top small rectangles label each column… n

Exterior Angle Inequality * Remote Int. + Remote Int. = Exterior Angle -The exterior angle is greater than either of the remote interior angles by themselves rem. Int. < ext. Ex: Inequality with Sides Inequality with Angles -The biggest side is across from the biggest angle -The smallest side is across from the smallest angle -The biggest angle is across from the biggest side/ the smallest angle is across from the smallest side Ex:

Lesson 5. 3 Indirect Proof

Steps to Completing and Indirect Proof: Assume that the conclusion is false n Then ________ (show that the assumption leads to a contradiction) This contradicts the given information that ________. n Therefore, _________ (rewrite the conclusion) must be true. n

Example Indirect Proof Given: 5 x < 25 Prove: x < 5 Assume that x 5. 2. Then, x = 6. So, 5(6) < 25 30 < 25 This contradicts the given information that 5 x < 25. 3. Therefore, x < 5 must be true. 1.

Example Indirect Proof Given: m is not parallel to n Prove: m 3 m 2 1. 2. 3. Assume that m 3 = m 2. Then, angle 3 and angle 2 are alternate interior angles. When alternate interior angles are congruent then the lines that make them are parallel. That means m and n are parallel. This contradicts the given information that m is not parallel to n. Therefore, m 3 m 2 must be true

Lesson 5. 4 The Triangle Inequality

Triangle Inequality Theorem n The sum of the lengths of any two sides of a triangle is greater than the length of the third side

Triangle Inequality Theorem Problems n Determine if the measures given could be the sides of a triangle. 16, 17, 19 16 + 17 = 33 yes, the sum of the two smallest sides is larger than the third side n 6, 9, 15 6 + 9 = 15 no, the sum of the two smallest sides is equal to the other side so it cannot be a triangle n n Find the range for the measure of the third side given the measures of two sides. 7. 5 and 12. 1 - 7. 5 < x < 12. 1 + 7. 5 4. 6 < x < 19. 6 n 9 and 41 41 -9 < x < 41 + 9 32 < x < 50 n

Lesson 5. 5 Inequalities Involving Two Triangles

On the other side of the foldable from Lesson 2 (3 column chart) SAS Inequality Theorem (Hinge Theorem) -When 2 sides of a triangle are congruent to 2 sides of another triangle, and the included angle of one triangle is greater than the included angle of the other triangle… Then, the side opposite the larger angle is larger than the side opposite the smaller angle SSS Inequality Theorem -When 2 sides of a triangle are congruent to 2 sides of another triangle, and the 3 rd side of a triangle is greater than the 3 rd side of the other triangle… Then, the angle opposite the larger side is larger than the angle opposite the smaller side Examples: Ex: