Chapter 5 Recursion can be a very effective

Chapter 5 Recursion can be a very effective technique for solving what would otherwise be extremely elaborate problems. Sample recursive applications include: Ø Backtracking algorithms. Ø Programming language definition. Ø Matrix operations. In addition, a solid understanding of recursion is helpful in analyzing the time complexity of algorithms. Recursion-related analysis techniques include: Ø Mathematical induction. Ø Recurrence relations. CS 240 Chapter 5 - Recursion Page 37

Recursive Backtracking: Flood Fill Algorithm Starting with a “seed” pixel that’s inside a polygonal region, recursively visit the four adjacent pixels, coloring any that haven’t been colored, and that aren’t on the polygon’s boundary. Reaching the boundary is the recursion’s termination condition. void floodfill(int x, int y) { if (!filled(x, y)) { color(x, y); floodfill(x-1, y); // Left floodfill(x+1, y); // Right floodfill(x, y-1); // Up floodfill(x, y+1); // Down } } Boundary pixel CS 240 Chapter 5 - Recursion Seed pixel LRUD-visited pixel Page 38

Recursive Grammars Example: A Simple Calculator Grammar Languages, in particular programming languages, are defined by their grammars, sets of recursive rules which provide syntax. program: END expr_list END Using this grammar, the following is a syntactically correct calculator program: expr_list: expression ; expr_list expression: term + expression term – expression term pi = 3. 1416; rad = 2. 5; ht = 10; area = pi * rad; surfacearea = 2 * (area + pi * rad * ht); END term: primary / term primary * term primary: NUMBER NAME = expression - primary ( expression ) CS 240 Recursive grammars are also prominent in more sophisticated languages, making the following language features possible: • nested loops, conditionals, function calls • cascaded operators (<<, >>, =, etc. ) • multiple cases in a switch statement Chapter 5 - Recursion Page 39

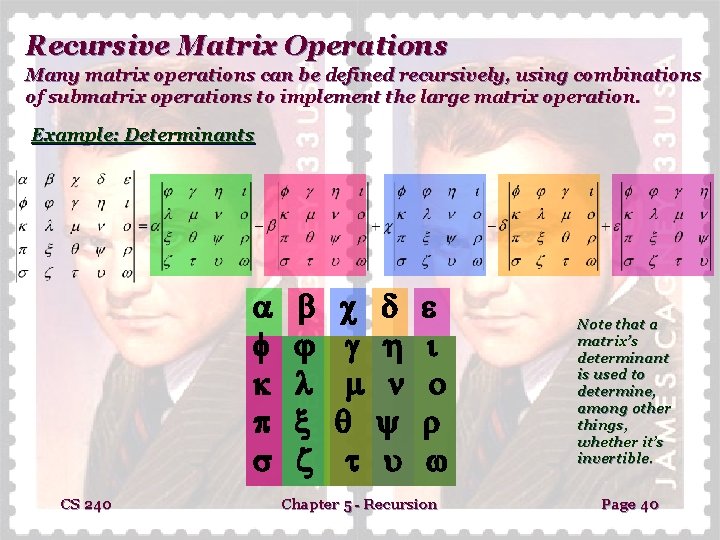
Recursive Matrix Operations Many matrix operations can be defined recursively, using combinations of submatrix operations to implement the large matrix operation. Example: Determinants CS 240 Chapter 5 - Recursion Note that a matrix’s determinant is used to determine, among other things, whether it’s invertible. Page 40

Recursive Determinant Program Example /////////////////// // Class definition file: matrix. h // // The matrix class has two data // // members: a square array of int- // // eger values (all between 0 and // // 9), and an integer indicating // // the array size. Its member // // functions include constructors, // // functions to set and access // // specific array elements, a // // function to access a subarray, // // a recursive determinant func// // tion, and an output operator. // /////////////////// // Member functions int get. Size() const { return size; } void set. Element(int i, int j, element. Type item); element. Type get. Element( int i, int j) { return table[i][j]; } element. Type determinant(); friend ostream& operator << (ostream &os, const matrix &m); protected: // Data members element. Type table[MAX_GRID_SIZE]; int size; #ifndef MATRIX_H #include <fstream> using namespace std; typedef int element. Type; const int MAX_GRID_SIZE = 7; class matrix { public: // Class constructors matrix() {size = 0; } matrix(const matrix &m); matrix(int sz); CS 240 // Member function matrix minor(int i, int j); }; #define MATRIX_H #endif Chapter 5 - Recursion Page 41

////////////////////// // Class implementation file: matrix. cpp // // The implementation of the copy and // // initializing constructors, the set. Ele- // // ment, determinant, and minor member // // functions, and the output operator. // ////////////////////// #include <cstdlib> #include <cassert> #include <fstream> #include <iomanip> #include <cmath> #include "matrix. h" using namespace std; // Copy constructor: Copies existing mat. // matrix: : matrix(const matrix &m) { size = m. size; for (int row = 0; row < m. size; row++) for (int col = 0; col < m. size; col++) table[row][col] = m. table[row][col]; } // Initializing constructor: Sets *this // // up as a sz x sz matrix of zeros. // matrix: : matrix(int sz) { size = sz; for (int row = 0; row < sz; row++) for (int col = 0; col < sz; col++) table[row][col] = 0; } CS 240 // Set. Element Member Function: Sets the // // (i, j) element of the matrix to item. // void matrix: : set. Element(int i, int j, element. Type e) { assert ((0<=i) && (i<size) && (0<=j) && (j<size)); table[i][j] = e; } // Determinant Member Function: Calculates // // & returns the determinant of the matrix. // element. Type matrix: : determinant() { element. Type value = 0; if (size == 1) return table[0][0]; for (int col = 0; col < size; col++) { value += (element. Type)pow(-1, 0+col) * table[0][col] * minor(0, col). determinant(); } return value; } Notice how the size×size matrix is being evaluated recursively by using the top row to expand into size (size-1)×(size-1) submatrices. Chapter 5 - Recursion Page 42

// Output Operator: Outputs matrix // // as a grid of size rows with // // size columns in each row. // ostream& operator << (ostream &os, const matrix &m) { for (int row = 0; row < m. get. Size(); row++) { for (int col = 0; col < m. get. Size(); col++) os << setw(4) << m. table[row][col]; os << endl; } return os; } CS 240 // Minor Member Function: If *this is // // an n. Xn matrix, then this returns // // the (n-1)X(n-1) matrix that is // // *this w/row i & column j removed. // matrix: : minor(int i, int j) { int subrow, subcol; assert (size > 1); matrix submat(size-1); subrow = 0; for (int row = 0; row < size; row++) { subcol = 0; if (row != i) { for (int col = 0; col < size; col++) if (col != j) { submat. set. Element(subrow, subcol, table[row][col]); subcol++; } subrow++; } } return submat; } Chapter 5 - Recursion Page 43

////////////////////////// // Program file: matrix. Driver. cpp // // This program tests the matrix class by // // creating a random matrix of a user-specified // // size, outputting it, & taking its determinant. // ////////////////////////// #include <iostream> #include <iomanip> #include <ctime> #include <cstdlib> #include "matrix. h" using namespace std; int generate. Random. Number(int lower. Bound, int upper. Bound); // The main function randomly generates & outputs // // a square matrix, , & determines its determinant. // void main() { int grid. Size; cout << "SPECIFY THE MATRIX SIZE (a positive " << "integer less than " << MAX_GRID_SIZE+1 << "): "; cin >> grid. Size; while ((grid. Size<1) || (grid. Size>MAX_GRID_SIZE)) { cout << "SORRY, ONLY VALUES BETWEEN 1 AND " << MAX_GRID_SIZE << " ARE ACCEPTED>n“; cout << "SPECIFY THE MATRIX SIZE (a positive " << "integer less than " << MAX_GRID_SIZE+1 << "): "; cin >> grid. Size; } CS 240 matrix grid(grid. Size); for (int row=0; row<grid. Size; row++) for (int col=0; col<grid. Size; col++) grid. set. Element(row, col, generate. Random. Number(0, 9)); cout << endl << "MATRIX: " << endl << grid << endl; cout << "DETERMINANT: " << grid. determinant() << endl; } // The generate. Random. Number function // randomly generates an integer in the // range between the parameterized low// er. Bound & upper. Bound values (inclu// sive). The first time it is called, // it seeds stdlib. h's random number // generation function rand(). int generate. Random. Number(int lower. Bound, int upper. Bound) { static bool first. Time = true; long int random. Number. Seed; if (first. Time) { time(&random. Number. Seed); srand(random. Number. Seed); first. Time = false; } return (lower. Bound + int((upper. Bound - lower. Bound) (float(rand()) / RAND_MAX))); } Chapter 5 - Recursion Page 44 // // *

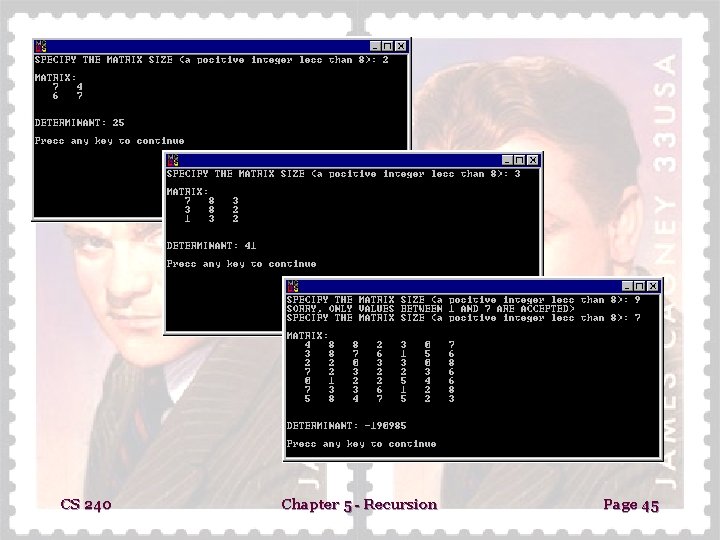
CS 240 Chapter 5 - Recursion Page 45

Mathematical Induction A mathematical “cousin” to recursion is the concept of induction. When you want to prove that something is true for all integer values, beginning at a specific value n 0, perform the following steps: Step One: Prove The Base Case Formally demonstrate that it’s true for that smallest value, n 0. Step Two: Assume For Some General Case Assume that the it’s true for all values through k, where k is at least n 0. Step Three: Prove For The Next Case Use the assumption that it’s true for smaller cases to prove that it’s also true for k+1. CS 240 Chapter 5 - Recursion Page 46

Induction Example Theorem A: i = 1, n i = ½n(n + 1) for all n 1. Proof (by induction): Step One (Prove for the base case): For n = 1, i = 1, 1 i = 1 = ½(1)(1 + 1). Step Two (Assume for some general case): Assume for n = k: i = 1, k i = ½k(k + 1). Step Three (Prove for the next case): Prove for n = k + 1: i = 1, k+1 i = (k + 1) + i = 1, k i = (k + 1) + ½k(k + 1) (by the assumption for case k) = ½(2)(k + 1) + ½k(k + 1) = ½(k + 1)(k + 2) = ½(k + 1)((k + 1). CS 240 Chapter 5 - Recursion Page 47

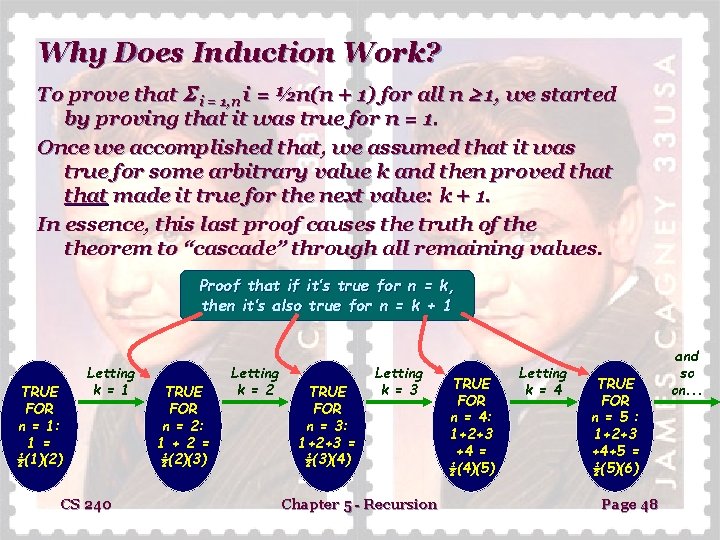
Why Does Induction Work? To prove that i = 1, n i = ½n(n + 1) for all n 1, we started by proving that it was true for n = 1. Once we accomplished that, we assumed that it was true for some arbitrary value k and then proved that made it true for the next value: k + 1. In essence, this last proof causes the truth of theorem to “cascade” through all remaining values. Proof that if it’s true for n = k, then it’s also true for n = k + 1 TRUE FOR n = 1: 1 = ½(1)(2) Letting k = 1 CS 240 TRUE FOR n = 2: 1 + 2 = ½(2)(3) Letting k = 2 TRUE FOR n = 3: 1+2+3 = ½(3)(4) Letting k = 3 Chapter 5 - Recursion TRUE FOR n = 4: 1+2+3 +4 = ½(4)(5) Letting k = 4 TRUE FOR n = 5 : 1+2+3 +4+5 = ½(5)(6) Page 48 and so on. . .

What’s Wrong With This Induction? Theorem Z: For any group of n people, all n have the same height. Proof (by induction): Step One (Prove for the base case): For n = 1, the group consists of a single person, so the entire group obviously has the same height. Step Two (Assume for some general case): Assume for n = k: Any group of k people have the same height. Step Three (Prove for the next case): Prove for n = k + 1: Given a group of k + 1 people, remove one person. The resulting group of k people must, by the inductive hypothesis, have the same height. Reinsert the person that was removed and then remove a different person. The resulting group of k people must also have the same height. Thus, all k + 1 people must have the same height! CS 240 Chapter 5 - Recursion Page 49

Recurrence Relations One of the bridges between recursion and induction is the recurrence relation, which can be used to determine the execution time of a recursive function. int power. Of 2(const int &n) { if (n == 0) return 1; return power. Of 2(n-1) + power. Of 2(n-1); } Assuming that the execution time for arithmetic operations, condition checking, and returning are all the same, let’s also assume that there is a function T(n) such that it takes T(k) time to execute power. Of 2(k). Examination of the code above allows us to conclude the following two facts: CS 240 T(0) = 2 T(k) = 5 + 2 T(k-1) for all k > 0 Chapter 5 - Recursion Page 50

T(0) = 2 T(k) = 5 + 2 T(k-1) for all k > 0 Using mathematical induction, we can prove that: T(k) = 7(2 k)-5 for all k 0 Step One (Prove for the base case): For n = 0, we already know that T(0) = 2, and 7(20)-5 also evaluates to 2. Step Two (Asume for some general case): Assume for n = k: T(k) = 7(2 k)-5. Step Three (Prove for the next case): Prove for n = k + 1: We know that T(k+1) = 5 + 2 T(k), and we’re assuming that T(k) = 7(2 k)-5, so we can conclude that T(k+1) = 5 + 2(7(2 k)-5) = 7(2 k+1)-5, which is what we wanted. CS 240 Chapter 5 - Recursion Page 51

One More Example. . . Let’s try the same trick on this alternate form of the function. int power. Of 2(const int &n) { if (n == 0) return 1; return 2*power. Of 2(n-1); } Using the same assumptions as before, we get the following recurrence relation: T(0) = 2 T(k) = 4 + T(k-1) for all k > 0 This time, however, mathematical induction tells us that: T(k) = 4 k+2 for all k 0 CS 240 Chapter 5 - Recursion Page 52