Chapter 5 Quality Assurance and Calibration Methods The

Chapter 5 Quality Assurance and Calibration Methods

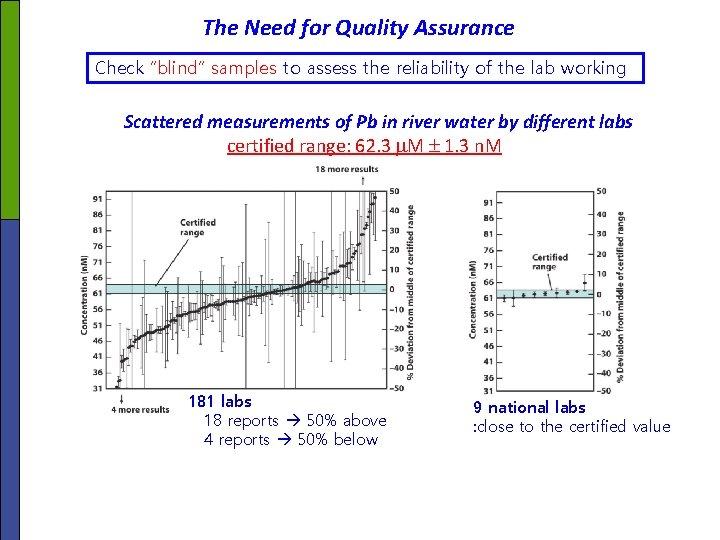
The Need for Quality Assurance Check “blind” samples to assess the reliability of the lab working Scattered measurements of Pb in river water by different labs certified range: 62. 3 M 1. 3 n. M 181 labs 18 reports 50% above 4 reports 50% below 9 national labs : close to the certified value

p p Quality assurance is what we do get the right answer for our purpose. : The answer should have sufficient accuracy and precision. In this Chapter, 1) Procedures in quality control and 2) Introduction of two more calibration methods Data quality standards: • Get the right date • Get the data right • Keep the date right

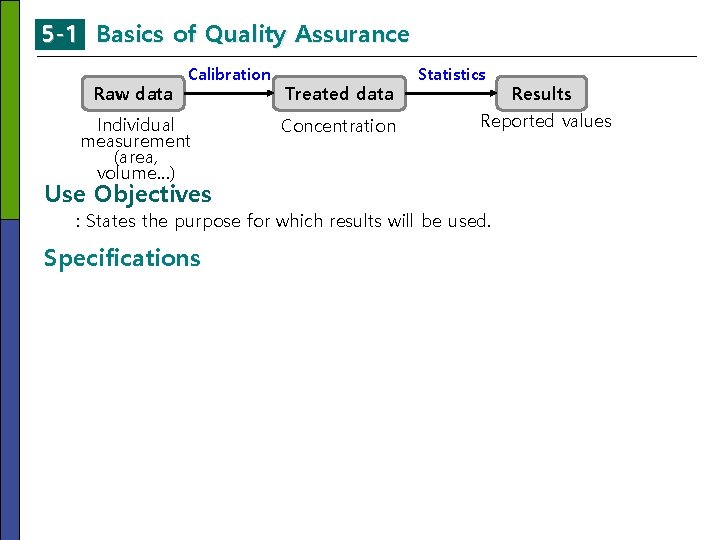
5 -1 Basics of Quality Assurance Raw data Calibration Individual measurement (area, volume…) Use Objectives Treated data Concentration Statistics Results Reported values : States the purpose for which results will be used. Specifications

§ Sensitivity = slope(m) of calibration curve change of signal = change in analyte concentration § Accuracy; uses standard reference materials(SRMs) § Blanks - Cause interferences (changing signal of analyte) from solvent, reagent, apparatus, instrument, and environment except analyte - Method/Reagent/Field blank - The blank can either be subtracted from analyte signal, or used as zero point in calibration. § Matrix - The medium containing analyte. - Everything in the unknown, other than analyte. (Everything else in sample other than analyte) - A matrix effect is a change in the analytical signal caused by anything in the sample other than analyte.

§ Spike recovery - Add a small volume of concentrated standard to sample solution - Avoid matrix effect - Confirm the signal of analyte Example Spike Recovery Result of unknown sample= 10. 0 ug/L Spiked known sample = 5. 0 ug/L → Concentration of spiked sample = 14. 6 ug/L ⇒ Percent recovery? Solution Cspiked sample – Cunspiked sample Percent recovery = X 100 Cadded 14. 6 μg/L – 10. 0 μg/L = X 100 5. 0 μg/L = 92 % (5 -1)

§ Calibration checks - Periodically check - Analyzed solution formulated to contain known concentration of analyte - Ensure that out instrument continues to work properly and calibration remains valid. § Performance test samples (quality control samples or blind samples) - To help eliminate bias - Use samples of known composition (SRMs) • To gauge accuracy: - calibration checks - spike recovery - quality control samples - blanks • To gauge precision: - replicate samples - replicate portions of a sample

Assessment is the process of 1) collecting data to show that analytical procedures are operating within specified limits and 2) verifying that final results meet use objectives. Control charts (Box 5 -1) p Shut down conditions from control chart n n n 1 outside the action lines 2 out of 3 consecutive measurements in the warning zones 7 consecutive measurements all above or all below the center line 6 consecutive measurements all steadily increasing or steadily decreasing 14 consecutive measurements alternating up and down obvious nonrandom pattern

5 -2 Method Validation • Validation determines the suitability of an analysis for providing the desired information. • Validation can apply to sample, to methodologies, and to date. • Validation is often done by the analyst but can also be done by supervisory personal. § Method validation; the process of proving that an analytical method is acceptable for its intended - Specificity - Accuracy & precision - Linearity & range; linear range vs. dynamic range vs. linear dynamic range vs. range - Robustness; not affected by small changes in conditions - LOD, LOQ

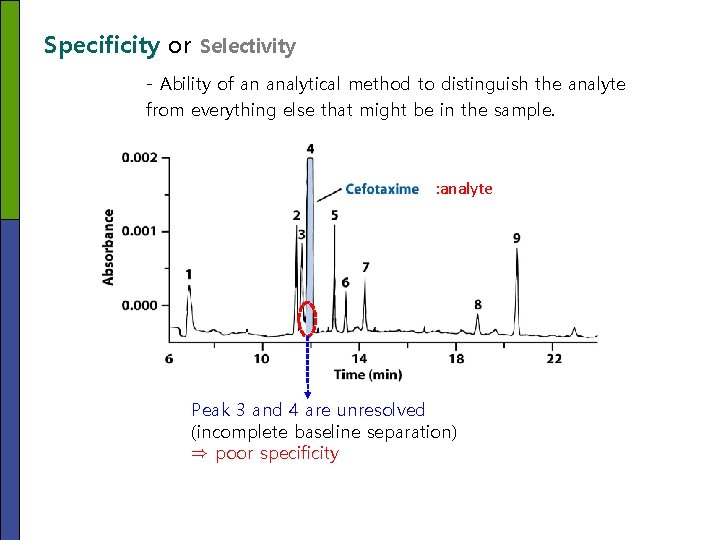
Specificity or Selectivity - Ability of an analytical method to distinguish the analyte from everything else that might be in the sample. : analyte Peak 3 and 4 are unresolved (incomplete baseline separation) ⇒ poor specificity

Linearity - The R 2 (square of correlation coefficient) values must be very close to 1 to represent a linear fit. - A y-intercept of calibration curve (after the response of the blank has been subtracted from each standard) should be close to 0(zero). - Range of R 2 value = 0~1 2 (5 -2) - R near 1 indicates that a regression line fits the data well. - For major component: >0. 995 (or ~0. 999) Accuracy Nearness to the truth § Ways to determine accuracy (systematic error) - Analyze a certified reference material as a standard (known composition and concentration) - Compare your results from two or more different analytical method - Analyze “blank” samples spiked with a known addition of analyte. : The matrix must be same as your unknown sample - Make standard additions(Section 5 -3) of analyte to the unknown sample

How is accuracy established ? While precision is easy to measure simply by replication, a measurement of accuracy involves comparing the experimental results to a “known” or “true” value. ⇒ Reference Methods or Standard Reference Materials. http: //www. nist. gov/srm/index. cfm

§ Types of precisions - Instrumental precision (or injection precision): the reproducibility observed when the same quantity of one sample is repeated introduced (precision for repeated sample loading) - Intra-assay precision: analyzing aliquots of a homogeneous material several times by on person on one day with the same equipment. - Intermediate precision (or Ruggedness): observed when an assay

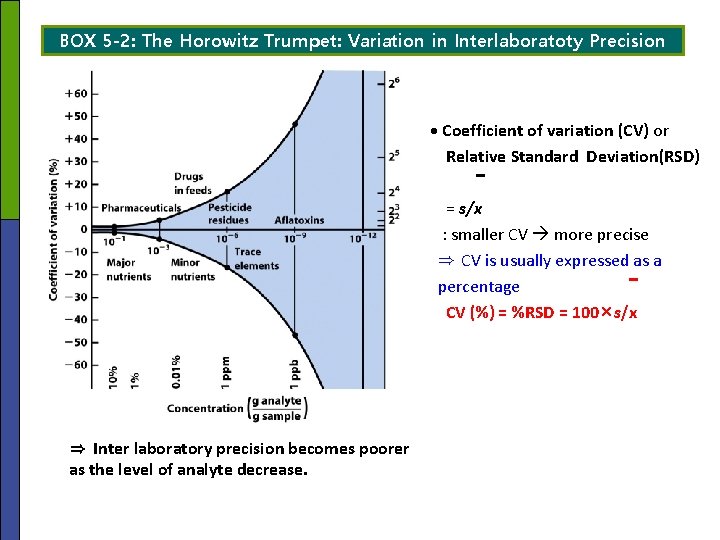
BOX 5 -2: The Horowitz Trumpet: Variation in Interlaboratoty Precision · Coefficient of variation (CV) or Relative Standard Deviation(RSD) = s/x : smaller CV more precise ⇒ CV is usually expressed as a percentage CV (%) = %RSD = 100×s/x ⇒ Inter laboratory precision becomes poorer as the level of analyte decrease.

Range : Concentration range over which linearity, accuracy, and precision meet specifications for analytical method. • for Major component Correlation coefficient(linearity): R 2≥ 0. 999 Spike recovery(accuracy): 100± 2% Interlaboratory precision: ± 3% • for Impurity Correlation coefficient: R 2≥ 0. 98 Spike recovery: 100± 10% Interlaboratory precision: ± 15%

Limits of Detection and Quantitation § Detection limit (DL or Lower limit Of Detection(LOD)); the smallest quantity of analyte that is “significantly different” from the blank. 1) 2) 3) 4) 5) Procedures for Determination of Detection Limit (DL, LOD) Prepare a sample whose concentration is ~1 to 5 times the detection limit. Measure the signal from n replicate samples (n≥ 7). Compute the standard deviation(s) of the n measurements. Measure the signal from n blanks and find the mean, yblank. The minimum detectable signal(ydl) is defined as S/N = 3 (5 -3) ydl = yblank + 3 s Signal (S) (5 -3) Noise (N) 6) Corrected signal (ysample – yblank) is proportional to sample concentration: ysample – yblank = m×sample concentration (5 -4) ysample = m×sample concentration + yblank ydl = m×LOD + yblank + 3 s = m×LOD + yblank where, y = signal of sample ⇒ Minimum detectable concentration (DL) 3 s LOD(DL) = (5 -5) m sample yblank = signal of blank m = slope of the linear calibration curve s = SD of sample signal • Lower limit of Quantification (LOQ); Lower limit of quantification, or the smallest amount that can be measured with reasonable accuracy. LOQ = 10 s m (5 -6)

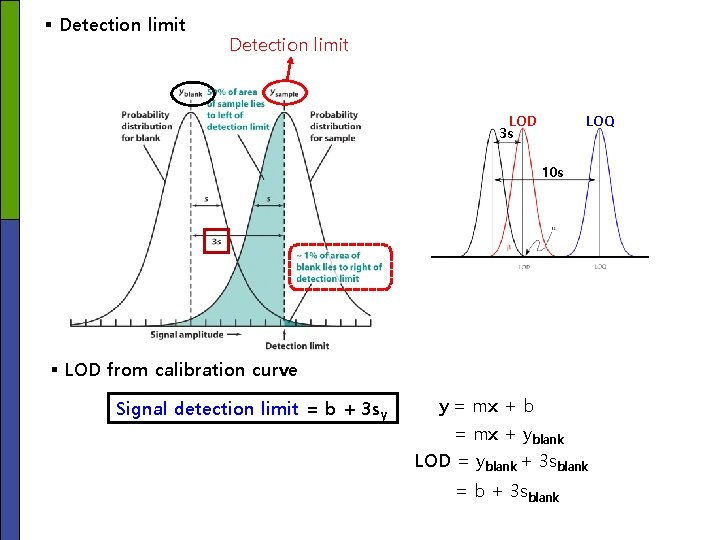
§ Detection limit LOD 3 s LOQ 10 s § LOD from calibration curve Signal detection limit = b + 3 sy y = mx + b = mx + yblank LOD = yblank + 3 sblank = b + 3 sblank

5 -3 Standard Addition To be useful, a calibration curve must: • Have a defined relationship a measurable quantity (usually concentration) and the signal measure. • Often this relationship is linear, but other relationships can also be useful. • Be collected under the same, or near same, conditions as what exists for the analyte. - Similar matrix - Similar species - Similar experimental conditions (sample holder, lab temperature, instrument settings, etc. ) • A minimum of 3 data points over a range of concentrations should be collected to define the line (or other calibration relationship). The concentration of the analyte must lie within the calibration range.

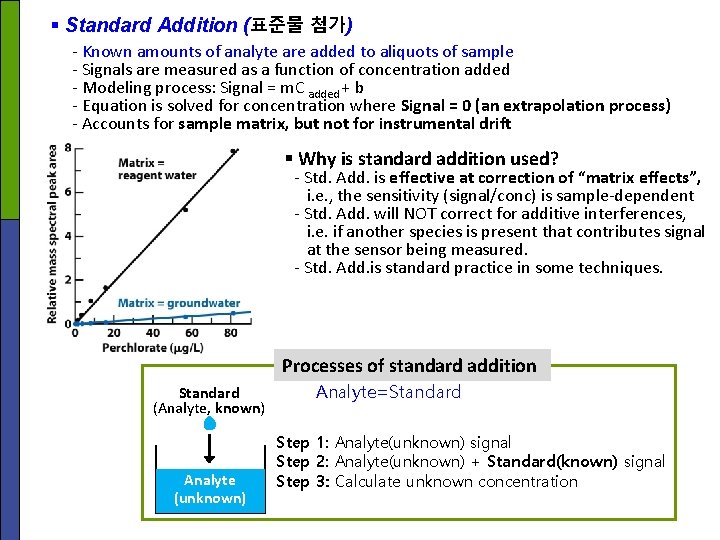
§ Standard Addition (표준물 첨가) - Known amounts of analyte are added to aliquots of sample - Signals are measured as a function of concentration added - Modeling process: Signal = m. C added + b - Equation is solved for concentration where Signal = 0 (an extrapolation process) - Accounts for sample matrix, but not for instrumental drift § Why is standard addition used? - Std. Add. is effective at correction of “matrix effects”, i. e. , the sensitivity (signal/conc) is sample-dependent - Std. Add. will NOT correct for additive interferences, i. e. if another species is present that contributes signal at the sensor being measured. - Std. Add. is standard practice in some techniques. Processes of standard addition Standard (Analyte, known) Analyte (unknown) Analyte=Standard Step 1: Analyte(unknown) signal Step 2: Analyte(unknown) + Standard(known) signal Step 3: Calculate unknown concentration

Concentration of analyte in initial solution Concentration of analyte plus standard in final solution Standard addition equation: Where, (5 -7) Total volume(V) = V 0 + Vs (5 -8) Dilution factor [S]f = (2. 08 M)(5. 00 m. L/100 m. L)=0. 104 M [X]f = [X]i(95. 0 m. L/100. 0 m. L) ∴[X]i = [Na+]i = 0. 113 M = signal from initial solution signal from final solution (X(analyte, unknown) =S(standard, known)) [X]i: initial conc. of analyte [X]f: diluted conc. of analyte [S]f: conc. of standard in the final solution [S]i: conc. of standard solution V 0: initial volume of unknown Vs: added volume of standard

Graphical Procedure for Standard Addition to a Single Solution VS V V 0 Increasing standard (known, S): IS+X Analyte(unknown, X): IX 9 points (=Is+x) (5 -9) y m (=[S]f) x (5 -10) Sy : SD of y, m ; slope of the line, y ; mean value of y (nine points) xi ; the individual values of x (nine points), x ; mean value of x (nine points) n ; number of date points for the calibration line

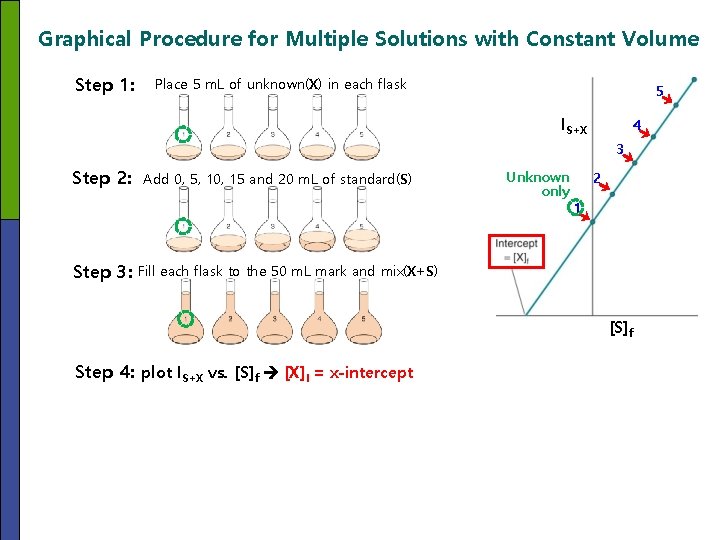
Graphical Procedure for Multiple Solutions with Constant Volume Step 1: Place 5 m. L of unknown(X) in each flask 5 IS+X 4 3 Step 2: Add 0, 5, 10, 15 and 20 m. L of standard(S) Unknown only 2 1 Step 3: Fill each flask to the 50 m. L mark and mix(X+S) [S]f Step 4: plot IS+X vs. [S]f [X]I = x-intercept

5 -4 internal Standards • A substance known as an “internal standard” is added to samples and standards (chemically similar to analyte) • Used to correct for instrumental drift (changes in sensitivity over time) and matrix effects (sample-related changes in sensitivity) § Requirements for an internal standard - Technique must be multi component-must separately measure signals for analyte and internal standard - No interferences: between analyte and internal std or between sample matrix and internal std - Internal standard must emulate drift and matrix effect behavior - Internal standard is not native in the sample

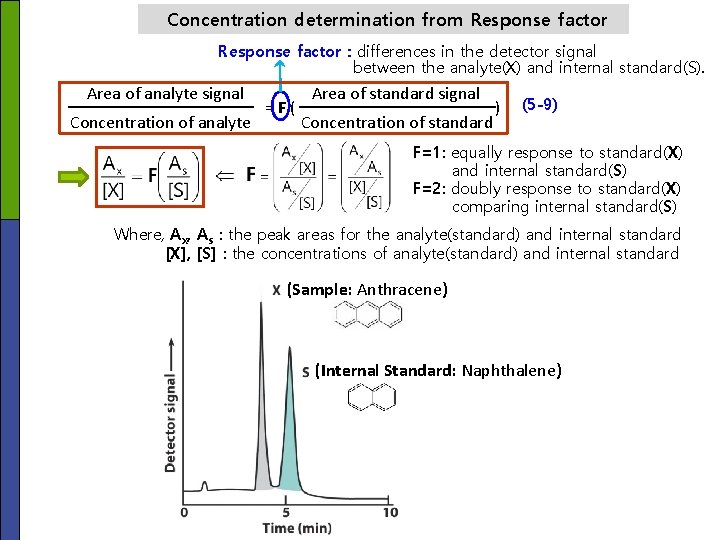
Concentration determination from Response factor : differences in the detector signal between the analyte(X) and internal standard(S). Area of analyte signal Concentration of analyte =F( Area of standard signal Concentration of standard ) (5 -9) F=1: equally response to standard(X) and internal standard(S) F=2: doubly response to standard(X) comparing internal standard(S) Where, Ax, As : the peak areas for the analyte(standard) and internal standard [X], [S] : the concentrations of analyte(standard) and internal standard (Sample: Anthracene) (Internal Standard: Naphthalene)

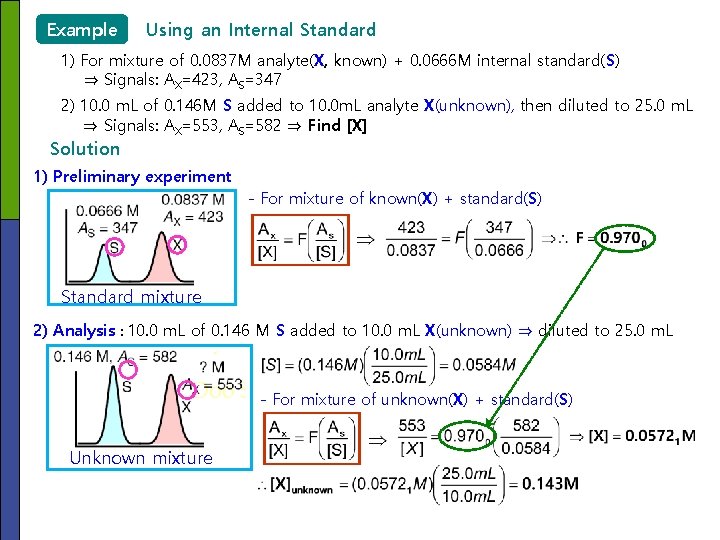
Example Using an Internal Standard 1) For mixture of 0. 0837 M analyte(X, known) + 0. 0666 M internal standard(S) ⇒ Signals: AX=423, AS=347 2) 10. 0 m. L of 0. 146 M S added to 10. 0 m. L analyte X(unknown), then diluted to 25. 0 m. L ⇒ Signals: AX=553, AS=582 ⇒ Find [X] Solution 1) Preliminary experiment - For mixture of known(X) + standard(S) Standard mixture 2) Analysis : 10. 0 m. L of 0. 146 M S added to 10. 0 m. L X(unknown) ⇒ diluted to 25. 0 m. L - For mixture of unknown(X) + standard(S) Unknown mixture

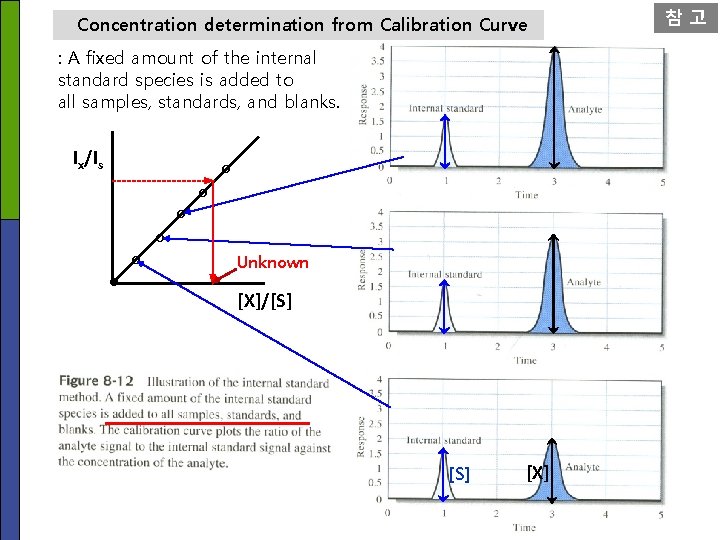
Concentration determination from Calibration Curve : A fixed amount of the internal standard species is added to all samples, standards, and blanks. Ix/Is o o o Unknown [X]/[S] [X] 참고