Chapter 5 Probability Created by Kathy Fritz Can

Chapter 5 Probability Created by Kathy Fritz

Can ultrasound accurately predict the gender of a baby? The paper “The Use of Three-Dimensional Ultrasound for Fetal Gender Determination in the First Trimester” (The British Journal of Radiology [2003]: 448 -451) describes a study of ultrasound gender prediction. An experienced radiologist looked at 159 first trimester ultrasound images and made a gender prediction for each one. When each baby was born, the ultrasound gender prediction was compared to the baby’s actual gender. This table summarizes the resulting data:

Radiologist 1 Predicted Male Predicted Female Baby is Male 74 12 Baby is Female 14 59 Notice that. All theof gender prediction based can on these questions be d e t c i d e r p D t a always correct. a. NOT oietstis h ultrasound image s i y l e t. Ihsea ecusing How lik answered the methods t? r s r p o k c r s e i i r d l e gend correc l ofictthed gende e t dwhe r morby introduced this chapter. r a n The paper also included gender predictions d iffin ertehne baiobloygiis e liakesecond ly to b s e t c t m he first a radiologist, who looked at 154 m l e u babey? trimester o y t a d h l ou ke aan whe sh i s , e l f a m e e m f n s i ale? r e ultrasound inmages. d n e g d icte d e ? r k p n i e p h y t r e If s r u paint the n Radiologist 2 to d e e n l l i w you t a h t Predicted Male Predicted Female t i s i y l e k i l o, how d u o y f I nt? Baby is Male 8 repai 81 Baby is Female 7 58

Interpreting Probabilities Probability Relative Frequency Law of Large Numbers Basic Properties

Probability We often find ourselves in situations where the To is quantify the likelihood of an occurrence, a outcome uncertain: number between 0 and 1 can be assigned to an outcome. When a ticketed passenger shows up at the airport, she faces. Atwo possible outcomes: she is able to 1 take probability is a number(1)between 0 and thatthe flight, reflects or (2) she is likelihood denied a seat as a resultof ofsome the of occurrence overbooking by the airline and must take a later flight. outcome. Based on her past experience, the passenger believes that the chance of being denied a seat is small or unlikely.

Subjective Approach to Probability The subjective interpretation of probability is when a probability is interpreted as a personal measure of the strength of the belief that an outcome will occur. A probability of 1 represents a belief that the outcome will certainly occur. A probability of 0 represents a belief that the outcome will certainly NOT occur. All other probabilities fall between these Because different people may have different extremes. subjective beliefs, two they may assign different probabilities to the same outcome.

Relative Frequency Approach • A probability of 1 corresponds to an outcome that occurs 100% of the time. A probability of 0 corresponds to an outcome that occurs 0% of the time.

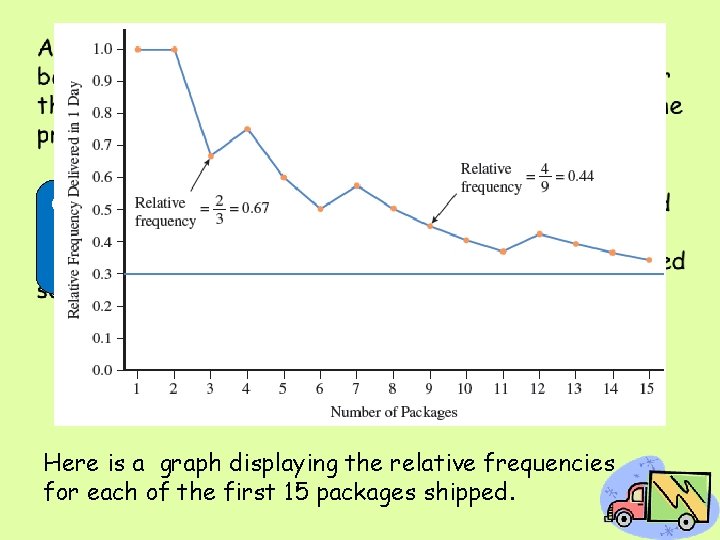
• One way to interpret this probability would be to say that in the long run, about 30 out of every 100 packages shipped arrive in 1 day. Here is a graph displaying the relative frequencies for each of the first 15 packages shipped.

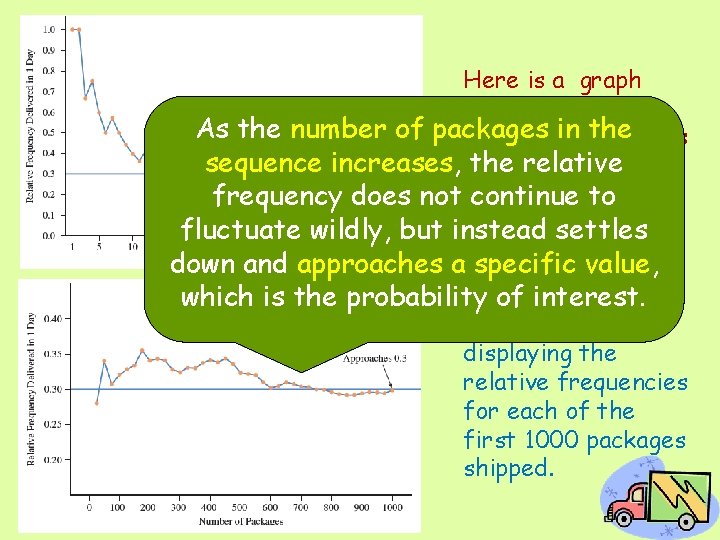
Here is a graph displaying the As the number of packages in the relative frequencies sequence increases, for theeach relative of the 50 packages frequency does not first continue to shipped. settles fluctuate wildly, but instead down and approaches a specific value, which is the probability of interest. Here is a graph displaying the relative frequencies for each of the first 1000 packages shipped.

Law of Large Numbers As the number of observations increases, the proportion of the time that an outcome occurs gets close to the probability of that outcome. The Law of Large Numbers is the basis for the relative frequency interpretation of probabilities.

Some Basic Properties of Probability 1. The probability of any outcome is a number between 0 and 1. 2. If outcomes can’t occur at the same time, then the probability that any one of them will occur is the sum of their individual probabilities.

A large auto center sells cars made by different manufacturers. Two these are Honda and Toyota. of many Suppose: P(Honda) = 0. 25 and P(Toyota) = 0. 14 An interpretation for this two value Why don’t these Consider the make ofabout the next car sold. Can the outcomes Honda and Toyota is that 25 out of probabilities have a every sumand of 1? happen at the time? 100 cars soldsame would be Hondas. What is the probability that the next car sold is either a Honda or a Toyota? P(Honda or Toyota) = 0. 25 + 0. 14 = 0. 39

Some Basic Properties of Probability 3. The probability that an outcome will not occur is equal to 1 minus the probability that the outcome will occur. Because a probability represents a long-run relative in situations exact Recall the frequency, car dealership (P(Honda)where = 0. 25): probabilities are not known, it is common to estimate probabilities based on observation. What is the probability that the next car sold is not a Honda? P(not Honda) = 1 - 0. 25 = 0. 75

Computing Probabilities Chance Experiment Sample Space Event Classical Approach to Probability

Chance Experiment A chance experiment is any activity or situation in which there is uncertainty about which of two or more outcomesof will result. experiments. Thesepossible are all examples chance These are the outcomes of chance experiments. Suppose two six-sided dice are rolled and they both land on sixes. Or a coin is flipped and it lands on heads. Or record the color of the next 20 cars to pass an intersection.

Sample Space The collection of all possible outcomes of a chance experiment is the sample space for the experiment. Sample space = {MH, FH, MT, FT} Consider a chance experiment to investigate whether men or women are more likely to choose a hybrid engine over a traditional internal combustion engine when purchasing a This an example of a sample Honda Civic at aisparticular dealership. The typespace. of vehicle purchased (hybrid or traditional) will be determined and the customer’s gender will be recorded.

Chance Experiment An event is any collection of outcomes from the sample space of a chance experiment. Recall the can situation in which a by person purchases Honda An event be represented a name, such asahybrid, Civic: or by Sample space letter, = {MH, such FH, MT, an uppercase as A, FT} B, or C. A simple is an event consisting of Eachevent of these 4 outcomes are simple events. exactly on outcome. Identify the following events: traditional = {MT, FT} female = {FH, FT}

Classical Approach to Probability • The classical approach to probability works well for chance experiments that have a finite set of outcomes that are equally likely.

Four students (Adam (A), Bettina (B), Carlos (C), and Debra(D)) submitted correct solutions to a math contest that had two prizes. The contest rules specify that if more than two correct responses are submitted, the winners will be selected at random from those submitting correct responses. What is the sample space for selecting the two winners from the four correct responses? Sample space = {AB, AC, AD, BC, BD, CD} Because the winners are selected at random, the six possible outcomes are equally likely.

Relative Frequency Approach to Probability • When a chance experiment is performed, some events may be likely to occur, whereas others may not be as likely to occur. In cases like these, the classical approach is not appropriate.

Suppose that you perform a chance experiment that consists of flipping a cap from a 20 -ounce bottle of soda and noting whether the cap lands with the top up or down. Do you think that the event U, the cap landing up, and event D, the You carry out thistop chance experiment by flipping landing areifequally the capcap 1000 timestop anddown, record it lands top up likely? Whylands or Why or top down. The cap top not? up 694 times.

Probabilities of More Complex Events Union Intersection Complement Mutually Exclusive Events Independents Events

Consider the chance experiment that consists of selecting a student at random from those enrolled at a particular college. There are 9000 students enrolled at the college Here are some possible events: F = event that the selected student is female O = event that the selected student is older than 30 A = event that the selected student favors the expansion of the athletic program S = event that the selected student is majoring is one of the lab sciences

Complement If E is an event, the complement of E, denoted EC, is the event that E does not occur. What is the probability of event A not occurring?

Intersection • This is the symbol for “intersection”. Consider the events: O = event that the selected student is older than 30 S = event that the selected student is majoring is one of the lab science This table summaries the occurrence of these events:

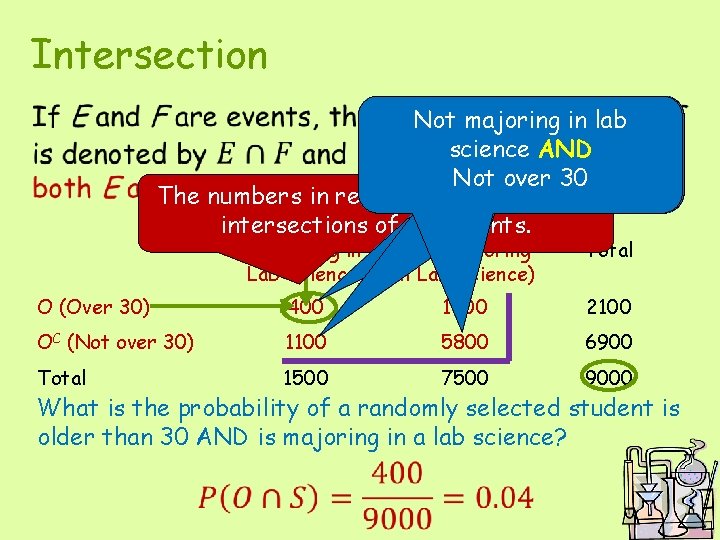
Intersection • Majoring Not majoring in lab in science lab science ANDAND Not Over over 3030 The numbers in red corresponds to the S SC intersections of the events. (Majoring in Lab Science) (Not Majoring in Lab Science) Total O (Over 30) 400 1700 2100 OC (Not over 30) 1100 5800 6900 Total 1500 7500 9000 What is the probability of a randomly selected student is older than 30 AND is majoring in a lab science?

Union • This is the symbol for “union”. Consider the events: O = event that the selected student is older than 30 A = event that the selected student favors the expansion of the athletic program This table summaries the occurrence of these events:

Union • The event O, over 30 The event A, favors sale of alcohol A (Favors Expansion) AC (Does Not Favor Expansion) Total O (Over 30) 1600 500 2100 OC (Not over 30) 2700 4200 6900 Total 4300 4700 9000 What is the probability of a randomly selected student is older than 30 OR favors the expansion of the athletic program?

Hypothetical 1000 You can use tables to compute the probability of an intersection of two events and the probability of a union of two events. Inmany situations, you may ONLY know the previous examples, this was possible because a probabilities some events. In this case, it is student was of to be selected at random and because often possible to create a “hypothetical 1000” the number of students falling into each of the cells the appropriate tabletowere given. table andofthen use the table compute probabilities.

The report “TV Drama/Comedy Viewers and Health Information” (www. cdc. gov/healthmarketing) describes a large survey that was conducted by the Centers for Disease Control (CDC). The CDC believed that the sample was representative of adult Americans. Let’s investigate these events (taken from questions on the survey): L = event that a randomly selected adult American reports learning something new about a health issue or disease from a TV show in the previous 6 months. F = event that a randomly selected adult American is female.

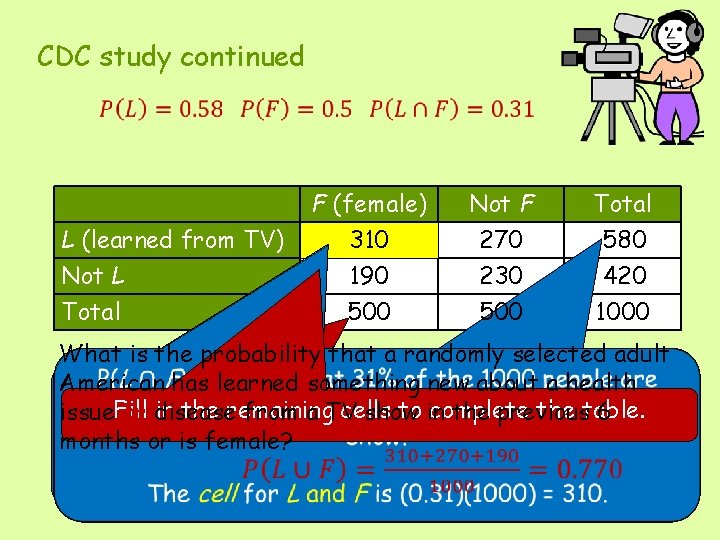
CDC study continued L (learned from TV) Not L Total F (female) Not F Total 310 270 580 190 500 230 500 420 1000 What is the probability that a randomly selected adult American has learned something new about healthbe P(L) tells you that 58% of the 1000 peopleashould P(F) tells you that the F row is (0. 50)(1000) = 500 Begin by labeling rows and columns of the table. in the remaining cells to in complete the table. issue. Fill or disease from a TV show the= previous 6 Put in the L row: (0. 58)(1000) 580. and the “hypothetical 1000” in the bottom right cell. months or is female? that the Not F row is 1000 - 500 = 500 The L row and the Not L row have a sum of 1000.

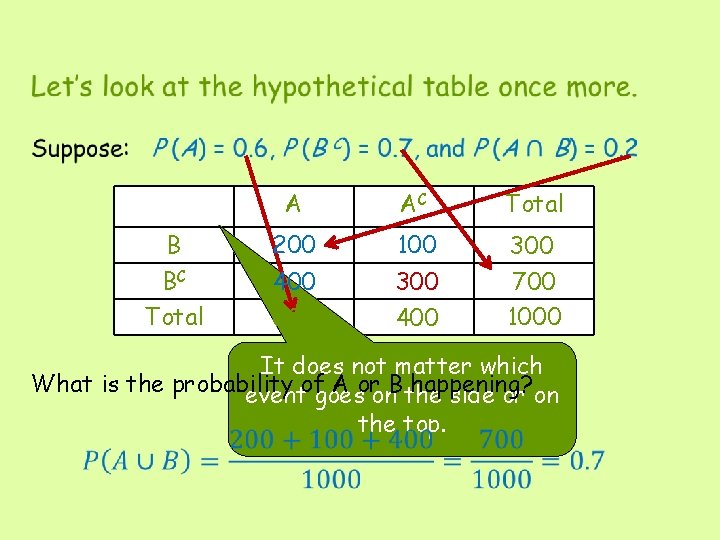
• B BC Total A AC Total 200 100 300 400 600 300 400 700 1000 It does not matter which What is the probability A oron. Bthe happening? eventofgoes side or on the top.

Mutually Exclusive Events Two events E and F are mutually exclusive if they can NOT occur at the same time. Sometimes people call the emergency 9 -1 -1 number to report situations that are not considered emergencies (such as to report a lost dog). Let two events be: M = event that the next call to 9 -1 -1 is for a medical emergency N= event that the next call to 9 -1 -1 is not considered an emergency Suppose that you know P(M) = 0. 30 and P(N) = 0. 20. Events M and N are mutually exclusive because the next call can’t be both a medical emergency and a call that is not considered an emergency.

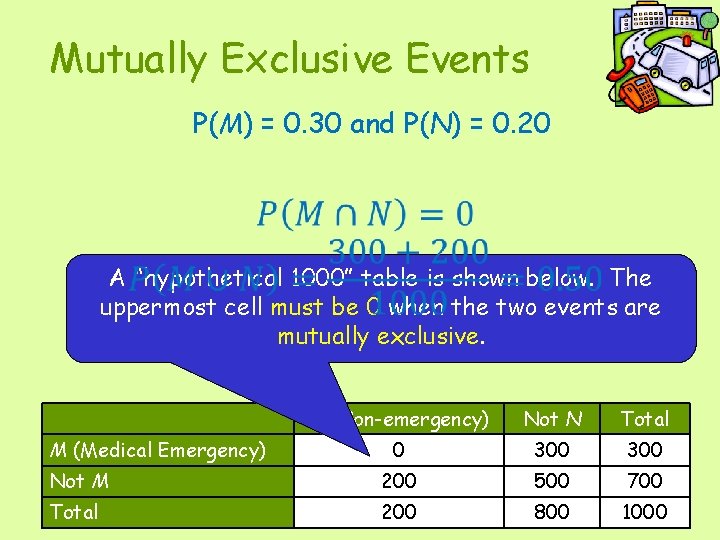
Mutually Exclusive Events P(M) = 0. 30 and P(N) = 0. 20 A “hypothetical 1000” table is shown below. The uppermost cell must be 0 when the two events are mutually exclusive. N (Non-emergency) Not N Total 0 300 Not M 200 500 700 Total 200 800 1000 M (Medical Emergency)

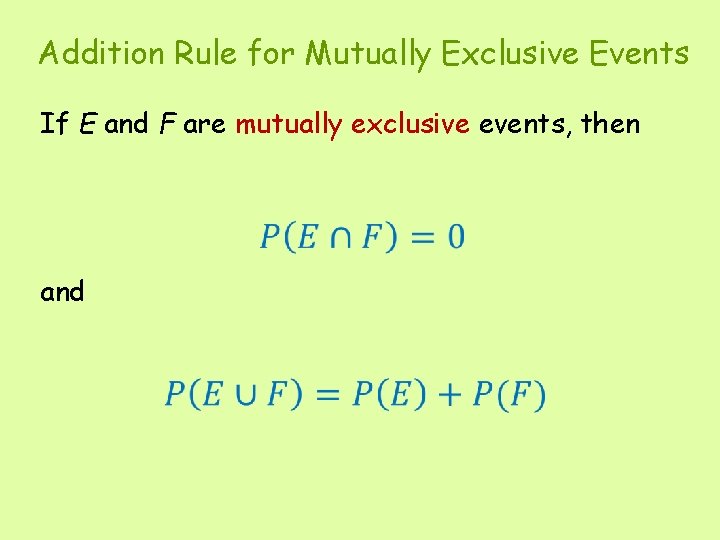
Addition Rule for Mutually Exclusive Events If E and F are mutually exclusive events, then and

Independent Events Two events are independent if the probability Because twooccurs components operate independently of that one the event is not affected by each other, learning that monitor hashas needed knowledge of whether thethe other event warranty service would not effect your assessment of occurred. the likelihood that the keyboard will need repair. Suppose that you purchase a desktop computer system with a separate monitor and keyboard. Two possible events are: Event 1: The monitor needs service while under warranty. Event 2: The keyboard needs service while under warranty.

Dependent Events Two events are dependent if knowing that one event has occurred changes the probability that the other event occurs. Consider a university’s course registration process, which divides students into 12 priority groups. Overall, only 10% of all students receive all requested classes, but 75% of those in the first priority group receive all requested classes. You would say that the probability that a randomly selected student at this university receives all requested class is 0. 10. However, if you know that the selected student is in the first priority group, you revise the probability that the student receives all requested classes to 0. 75. These two events are said to be dependent events.

Multiplication Rule for Two Independent Events • More generally, if there are k independent events, the probability that all the events occur is the product of all individual event probabilities.

The Diablo Canyon nuclear power plant in California has a warning system that includes a network of sirens. When the system is tested, individual sirens sometimes fail. The sirens operate independently of one another. Imagine that you live near Diablo Canyon and that there are two sirens that can be heard from your home. You might be concerned about the probability that both Siren 1 and Siren 2 fail. (When the siren system is activated, about 5% of the individual sirens fail. ) Using the multiplication rule for independent events:

Conditional Probability

Sometimes the knowledge that one event has occurred changes our assessment of the likelihood that another event occurs. Consider a population in which 0. 1% of all the individuals have a certain disease. The presence of the disease cannot be discerned from appearances, but there is a diagnostic test available. Unfortunately, the test is not always correct. Suppose that 80% of those with positive test results actually have the disease and the other 20% of those with positive test results actually do NOT have the disease (false positive).

Disease example continued. . . Consider the chance experiment in which an individual is randomly selected from the population. Let: E = event that the individual has the disease F =vertical event that individual's The line the is read “given”. diagnostic test is This is an example of conditional probability. positive P(E|F) denotes the probability that event E (has disease) GIVEN that event F (tested positive) occurs.

Conditional Probability Conditional probability is a probability that takes into account a given condition has occurred. P(A|B) is read as the probability of event A occurring GIVEN event B has occurred.

Recall the example in the Chapter Preview section about gender predictions based on ultrasounds performed during the first trimester of pregnancy. The table below summarizes the data for Radiologist 1 Baby is Male Predicted Female Total 74 12 86 59 73 71 159 This question is about ALL Baby is Female 14 159 ultrasound predictions. Total 88 How likely is it that a predicted gender is correct?

Gender prediction example continued. Radiologist 1 Predicted Male Predicted Female Total Baby is Male 74 12 86 Baby is Female 14 59 73 Total 88 71 159 Is a predicted gender more likely to be correct when the baby is male than when the baby is female? This question is based on two conditions: the 86 male babies or the 73 female babies. The appropriate row total or column total is used Radiologist 1 is slightly in more to be correct when the as the denominator the likely probability calculation. baby is male than when the baby is female.

Gender prediction example continued. Radiologist 1 Male This is a Predicted condition. In the. Predicted probability Female statement, the condition follows the Baby is Male 74 vertical line “|”. 12 Total 86 Baby is Female 14 59 73 Total 88 71 159 If the predicted gender is female, should you paint the nursery pink? For Radiologist 1, when the predicted gender is female, about 83% of the time the baby is actually female. So, if you painted the room pink, then the probability that you would need to repaint is about 0. 17 (1 – 0. 83).

Let’s answer these questions: 1. What is the probability that a gender prediction based on a first-trimester ultrasound at this clinic is correct? 2. If the first-trimester ultrasound gender prediction is incorrect, what is the probability that the prediction was made by Radiologist 2?

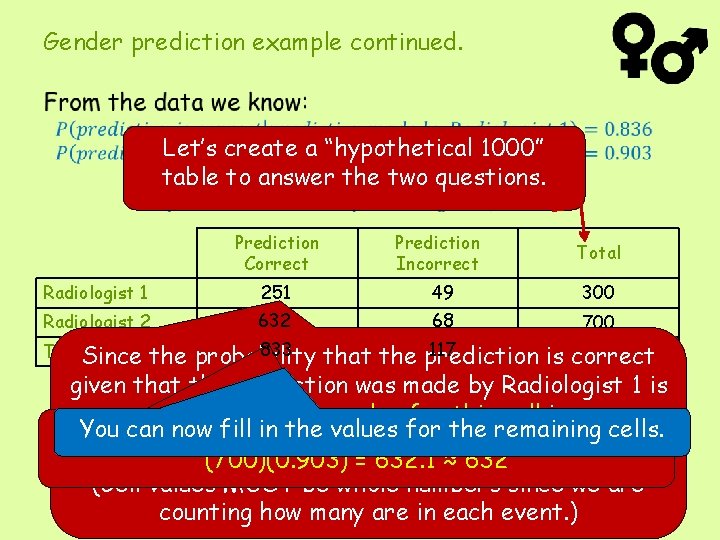
Gender prediction example continued. Let’s create a “hypothetical 1000” table to answer the two questions. Prediction Correct Prediction Incorrect Total Radiologist 1 251 49 300 Radiologist 2 632 68 700 833 117 1000 the probability that the prediction is correct given that the prediction was made by Radiologist 1 is 0. 836, then the value for this cell is: You can. Similarly, now fill inthe thevalues for thecell remaining cells. this (300)(0. 836) = for 250. 8 ≈ 251 is: (700)(0. 903) = 632. 1 ≈ 632 (Cell values MUST be whole numbers since we are counting how many are in each event. ) Total. Since

Gender prediction example continued. Prediction of. Correct the incorrect. Incorrect gender Total About 58. 1% predictions at 49 Radiologist 1 this clinic 251 are made by Radiologist 2. 300 Radiologist 2 700 2 This seems high 632 – but remember 68 that Radiologist 833 twice as many 117 predictions 1000 Total does more than as Radiologist 1. If theisfirst-trimester gender prediction is What the probabilityultrasound that a gender prediction based incorrect, what is theultrasound probability prediction was on a first-trimester atthat this the clinic is correct? made by Radiologist 2?

Calculating Probabilities – A More Formal Approach

Probability Formulas •

Probability Formulas Continued •

• What is the probability that a randomly selected adult American reports learning something new about a health issue or disease from a TV show in the previous 6 months or that a randomly selected adult American is female?

The article “Chances Are You Know Someone with a Tattoo, and He’s Not a Sailor” (Associated Press, June 11, 2006) summarized data from a representative sample of adults ages 18 to 50. T = the event that a randomly selected person has a tattoo A = the event that a randomly selected person is between 18 and 29 years old Notice that the probability of “A given T” and “T given A” are NOT the same!

Another Approach to Probability A large electronics store sells two different portable DVD players, Brand 1 and Brand 2. Based on past records, the store manager reports that 70% of the DVD players sold are Brand 1 and 30% are Brand 2. The manager also reports that 20% of the people who buy Brand 1 also purchase an extended warranty, and 40% of the people who buy Brand 2 purchase an extended warranty. Consider selecting a person at random from those who purchased a DVD player from this store, what is the probability that the person purchased extended warranty? One way to do this problem would be to set up a Hypothetical 1000 table.

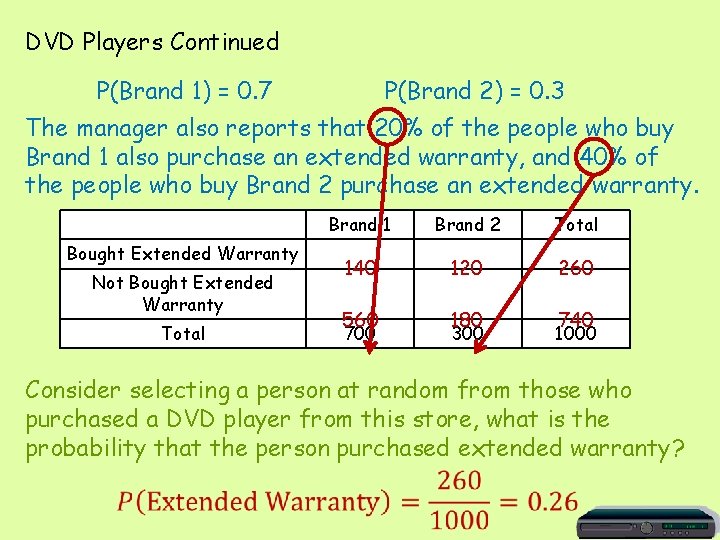
DVD Players Continued P(Brand 1) = 0. 7 P(Brand 2) = 0. 3 The manager also reports that 20% of the people who buy Brand 1 also purchase an extended warranty, and 40% of the people who buy Brand 2 purchase an extended warranty. Bought Extended Warranty Not Bought Extended Warranty Total Brand 1 Brand 2 Total 140 120 260 560 180 700 300 740 1000 Consider selecting a person at random from those who purchased a DVD player from this store, what is the probability that the person purchased extended warranty?

DVD Players Continued P(Brand 1) = 0. 7 P(Brand 2) = 0. 3 The manager also reports that 20% of the people who buy Brand 1 also purchase an extended warranty, and 40% of the people who buy Brand 2 purchase an extended warranty. Consider selecting a person at random from those who purchased a DVD player from this store, what is the probability that the person purchased extended warranty? B 1 = 0. 7 B 2 = 0. 3 and (0. 7)(0. 2) 0. 14 problem is Another approach to= this to use a tree diagram. EC = 0. 8 E = 0. 2 or E = 0. 4 This is an example of the Law of (0. 3)(0. 4) = 0. 12 Total Probability! EC = 0. 6 P(E) = 0. 14 + 0. 12 = 0. 26

The Law of Total Probability •

Let’s consider another type of problem. . . Suppose the conditional probability of “a positive test result given that the person has cancer” is known. However, you would like to know the converse probability. That is, you would like to know the probability of the person having cancer given a positive test result. This formula was discovered in the 1700’s by the Reverend Thomas probability Bayes, an English A converse is the reversal Presbyterian minister. probability. of a conditional This converse probability can be computed using Bayes’ Rule.

Bayes’ Rule • Let’s look at an example.

Internet addiction has been defined by researchers as a disorder characterized by excessive time spent on the Internet, impaired judgment and decision-making ability, social withdrawal, and depression. In a study of adolescents, each participant was assessed using the Chen Internet Addiction Scale to determine if he or she suffered from Internet addiction. The following probabilities are based on survey results: Although Bayes’ is not listed AP® Statistics P(F)Rule = 0. 518 P(M)in=the 0. 482 course description, are expected be able to solve P(I|F) = you 0. 131 P(I|M)=to 0. 248 “Bayes’-like” problems. Besides using the formula, you can What is the probability that a randomly selected adolescent also solve using tables or tree diagrams. from the survey is female given that she has Internet addiction?

Probability as a Basis for Making Decisions

Probability plays an important role in drawing conclusions from data. A professor planning to give a quiz that consists of 20 true-false questions is interested in knowing how someone who answers by guessing would do on such a quiz. To investigate, he asks the 500 students in his introductory psychology course to write the numbers from 1 to 20 on a piece of paper and then to arbitrarily write T or F next to each number. This table summarizes the number of The students are forced to guess at the to each correct answers onanswer the quiz. question, because they are not even told what the questions are! These answers are then collected and graded using the key for the quiz.

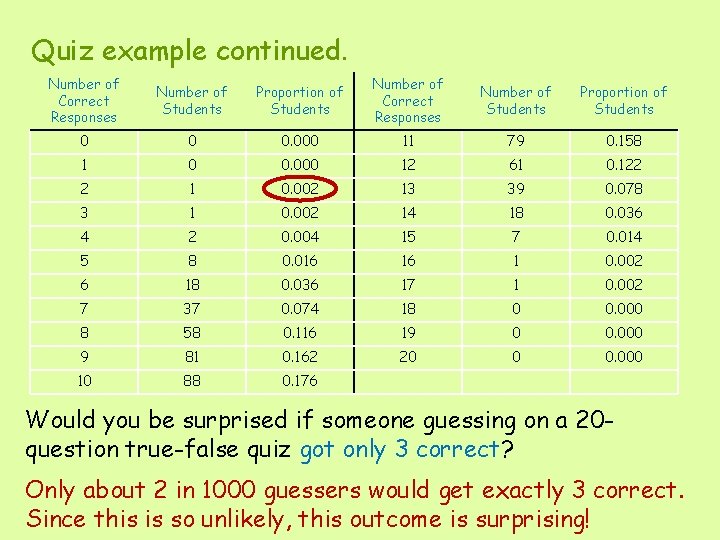
Quiz example continued. Number of Correct Responses Number of Students Proportion of Students 0 0 0. 000 11 79 0. 158 1 0 0. 000 12 61 0. 122 2 1 0. 002 13 39 0. 078 3 1 0. 002 14 18 0. 036 4 2 0. 004 15 7 0. 014 5 8 0. 016 16 1 0. 002 6 18 0. 036 17 1 0. 002 7 37 0. 074 18 0 0. 000 8 58 0. 116 19 0 0. 000 9 81 0. 162 20 0 0. 000 10 88 0. 176 Would you be surprised if someone guessing on a 20 question true-false quiz got only 3 correct? Only about 2 in 1000 guessers would get exactly 3 correct. Since this is so unlikely, this outcome is surprising!

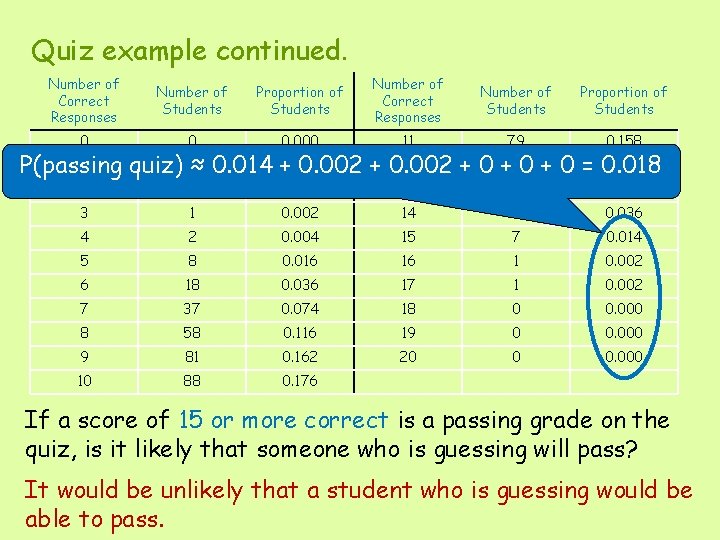
Quiz example continued. Number of Correct Responses Number of Students Proportion of Students 0 0 0. 000 11 79 0. 158 2 1 0. 002 13 39 0. 078 3 1 0. 002 14 18 0. 036 4 2 0. 004 15 7 0. 014 5 8 0. 016 16 1 0. 002 6 18 0. 036 17 1 0. 002 7 37 0. 074 18 0 0. 000 8 58 0. 116 19 0 0. 000 9 81 0. 162 20 0 0. 000 10 88 0. 176 1 12 0. 122 P(passing quiz) 0≈ 0. 014 +0. 000 0. 002 + 0 +610 + 0 = 0. 018 If a score of 15 or more correct is a passing grade on the quiz, is it likely that someone who is guessing will pass? It would be unlikely that a student who is guessing would be able to pass.

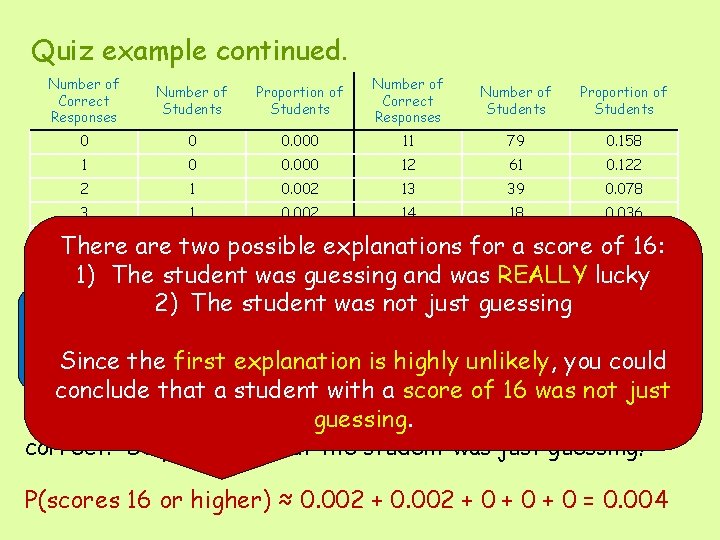
Quiz example continued. Number of Correct Responses Number of Students Proportion of Students 0 0 0. 000 11 79 0. 158 1 0 0. 000 12 61 0. 122 2 1 0. 002 13 39 0. 078 3 1 0. 002 14 18 0. 036 4 2 0. 004 15 0. 014 There are two possible explanations for 7 a score of 16: 5 8 0. 016 16 1 0. 002 1) The student was guessing 17 and was REALLY lucky 6 18 0. 036 1 0. 002 The student wasstudent not guessing 7 37 0. 074 the 18 just 0 0. 000 Begin by 2) assuming that was guessing and 8 58 19 0 determine whether a 0. 116 score at least as high as 16 0. 000 is a 9 81 0. 162 20 0 0. 000 Since the first explanation isoccurrence. highly unlikely, you could likely or an likely 10 88 0. 176 conclude that a student with a score of 16 was not just guessing. The professor actually gives the quiz, and a student scores 16 correct. Do you think that the student was just guessing? P(scores 16 or higher) ≈ 0. 002 + 0 + 0 = 0. 004

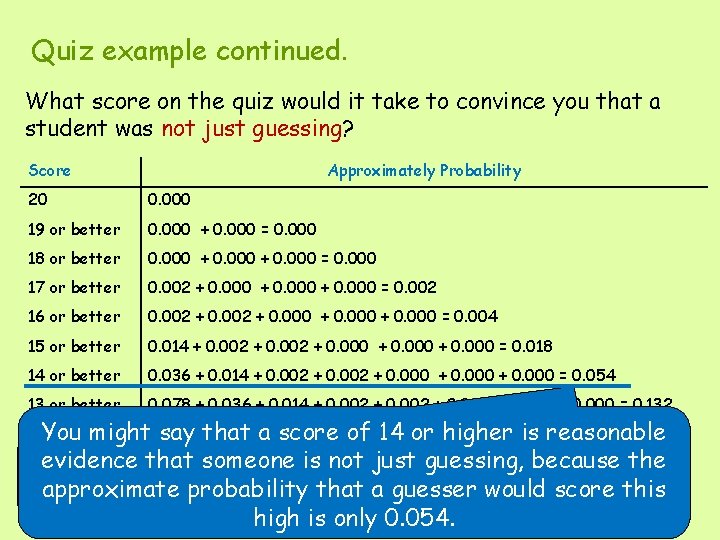
Quiz example continued. What score on the quiz would it take to convince you that a student was not just guessing? Score Approximately Probability 20 0. 000 19 or better 0. 000 + 0. 000 = 0. 000 18 or better 0. 000 + 0. 000 = 0. 000 17 or better 0. 002 + 0. 000 = 0. 002 16 or better 0. 002 + 0. 000 = 0. 004 15 or better 0. 014 + 0. 002 + 0. 000 = 0. 018 14 or better 0. 036 + 0. 014 + 0. 002 + 0. 000 = 0. 054 13 or better 0. 078 + 0. 036 + 0. 014 + 0. 002 + 0. 000 = 0. 132 You might say that a score of 14 or higher is reasonable Consider showing approximate probabilities for evidencethis thattable someone is not just guessing, because the a certain that scorea or higher. would score this approximate probability guesser high is only 0. 054.

Estimating Probabilities Empirically and Using Simulation

Estimating Probabilities Empirically It is fairly common practice to use observed longrun proportions to estimate probabilities. The process used to estimate probabilities is simple: 1. Observe a large number of chance outcomes under controlled circumstances. 2. Interpreting probability as a long-run relative frequency, estimate the probability of an event by using the observed proportion of occurrence.

To recruit a new faculty member, a university biology department intends to advertise for someone with a Ph. D. in biology and at least 10 years of college-level teaching experience. A similar university just would completed a search in which The biology like to determine the member ofdepartment the department express the belief thatthere was no requirement prior experience. probability applicant would be excluded becausewill of the requiring atan least 10 for years of teaching experience However, prior teachingapplicants experience was The experience requirement. exclude most potential and willrecorded. exclude more The probability that applicant be excluded resulting data is summarized in thewould following table. due female applicants than an male applicants. to the requirement of at 10 years experience is Number of least Applicants Less than 10 years 67. 5%. 10 or more years Total experience 277 138 This is just 178 a little more than two-thirds of the 112 290 applicants. 21 Female 99 120 Male Total 410

New faculty member example continued. Now let’s determine if more females than males are excluded due to the experience requirement. Number of Applicants It Male Less than 10 years experience 10 or more years experience Total appears that 178 female applicants are be 112 more likely to 290 excluded due to 99 the experience requirement than male Female 21 120 applicants. 138 Total 277 410

Estimating Probabilities by Using Simulation provides a way to estimate probabilities when: • You are unable to determine probabilities analytically • You do not have the time or resources to determine probabilities • It is impractical to estimate probabilities empirically by observation Simulations involves generating “observations” in a situation that is similar to the real situation of interest.

Using Simulation to Approximate a Probability 1. Design a method that uses a random mechanism (such as a random number generator or table, the selection of a ball from a box, or the toss a coin) to represent an observation. Be sure that the important characteristics of the actual process are preserved. 2. Generate an observation using the method in Step 1, and determine if the event of interest has occurred. 3. Repeat Step 2 a large number of times. 4. Calculate the estimated probability by dividing the number of observations for which the event of interest occurred by the total number of observations generated.

Suppose that couples who wanted children were to continue having children until a boy was born. Would this change the proportion of boys in the population? We will use simulation to estimate the proportion of boys in the population if couples were to continue having children until a boy was born. 1. You can use a single random digit to represent a child, where odd digits represent a male birth and even digits represent a female birth. 2. An observation is constructed by selecting a sequence of random digits. If the first random number obtained is odd (a boy), the observation is complete. If the first random number obtained is even (a girl), another digit is chosen. You would continue in this way until an odd digit is obtained.

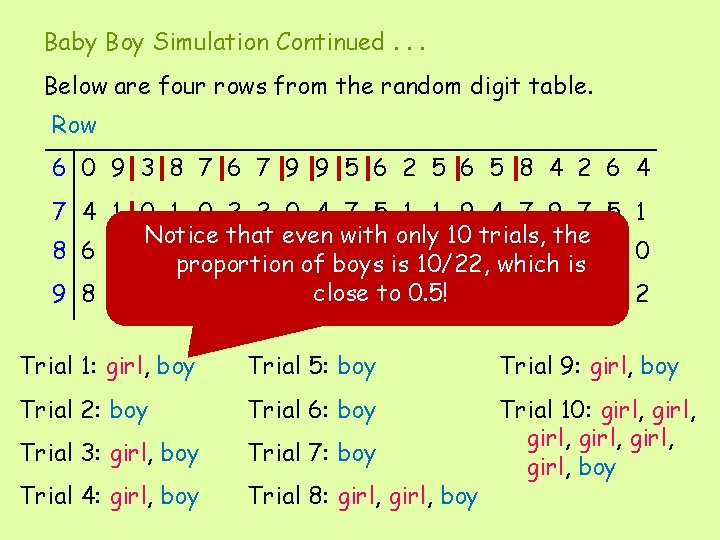
Baby Boy Simulation Continued. . . Below are four rows from the random digit table. Row 6 0 9 3 8 7 6 7 9 9 5 6 2 5 6 5 8 4 2 6 4 7 4 1 0 2 2 0 4 7 5 1 1 9 4 7 9 7 5 1 Notice that even with only 10 trials, the 8 6 4 7 3 6 3 4 5 1 2 3 1 1 8 0 0 4 8 2 0 proportion of boys is 10/22, which is 9 8 0 2 8 7 9 3 8 close 4 0 4 to 20. 5! 0 8 9 1 2 3 3 2 Trial 1: girl, boy Trial 5: boy Trial 9: girl, boy Trial 2: boy Trial 6: boy Trial 3: girl, boy Trial 7: boy Trial 4: girl, boy Trial 8: girl, boy Trial 10: girl, girl, boy