Chapter 5 Probabilistic test theory PTT Introduction q

Chapter 5: Probabilistic test theory (PTT): Introduction q PTT is concerned with the modeling of probabilities of response categories: q Probabilities of correct responses: Response options of participants are not necessarily identical to the response categories to be modeled. q Probabilities of response options: e. g. Probability distributions of ordered response categories of a rating scale.

Chapter 5: Probabilistic test theory (PTT): Introduction q Relationship between CTT and PTT: The general test model: q Both models assume response processes that are linear functions of exoge nousvariables. q PTT models comprise a non linear response function that maps the value of the latent response processes into the range [0, 1].

Chapter 5: Probabilistic test theory (PTT): Introduction q Relationship between CTT and PTT: The general test model: q Response processes: linear functions of exogenous variables: q CTT: Response processes are identical to observed variables:

Chapter 5: Probabilistic test theory (PTT): Introduction q Relationship between CTT and PTT: The general test model: q PTT: Response processes are latent variables (hidden res ponses that are mapped to probabilities (in the range of [0, 1]) by means of response functions. q This is due to the fact that PTT models model probabilities whereas CTT models are used for modeling means and covariances.

Chapter 5: PTT: Birnbaum models q Birnbaum models (Birnbaum, 1968) are used for model ing the probabilities in case of two response categories: 1 = correct response, and 0 = wrong response. q Three versions: 1 PL, 2 PL, & 3 PL models (one two and three parameter logistic models). All three models use the logistic response model: q Models are nested: The simpler models result from the more complex model by fixing parameters.

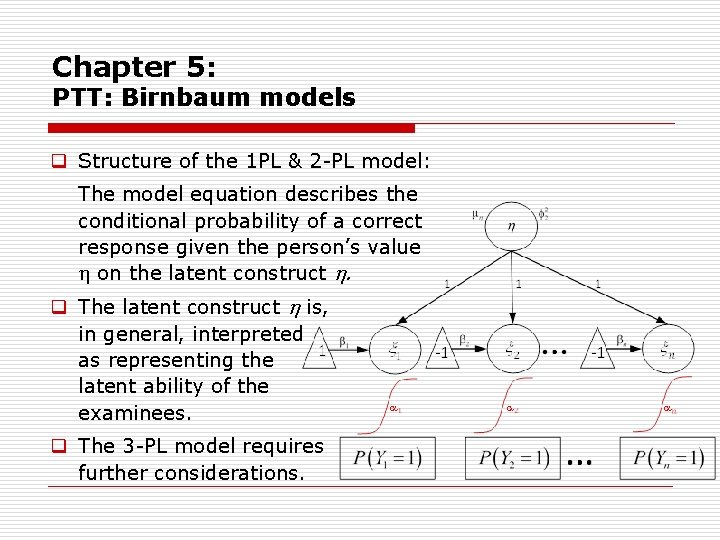
Chapter 5: PTT: Birnbaum models q Structure of the 1 PL & 2 PL model: The model equation describes the conditional probability of a correct response given the person’s value on the latent construct . q The latent construct is, in general, interpreted as representing the latent ability of the examinees. q The 3 PL model requires further considerations.

Chapter 5: PTT: Rasch Model (1 -PL) q Model equation of the Rasch model (1 PL): q = Value of the latent construct (the person’s ability). q i = Item difficulty. q q is the (conditional) probability of a correct response given a specific value of the person’s ability. increases with and decreases with i.

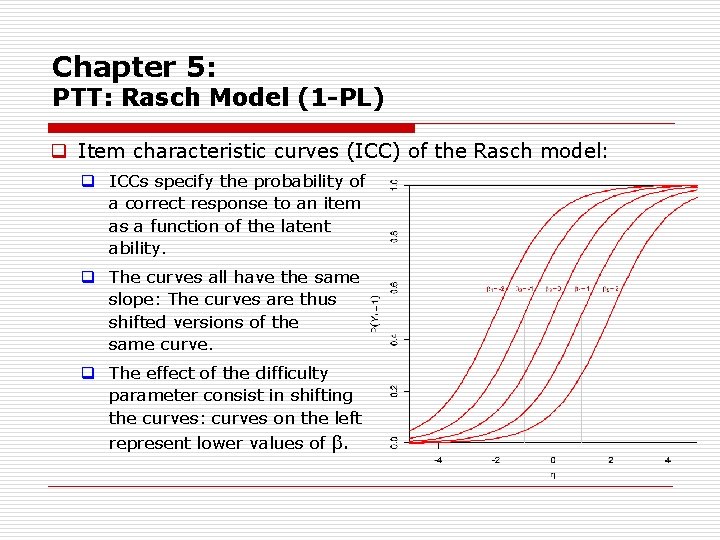
Chapter 5: PTT: Rasch Model (1 -PL) q Item characteristic curves (ICC) of the Rasch model: q ICCs specify the probability of a correct response to an item as a function of the latent ability. q The curves all have the same slope: The curves are thus shifted versions of the same curve. q The effect of the difficulty parameter consist in shifting the curves: curves on the left represent lower values of .

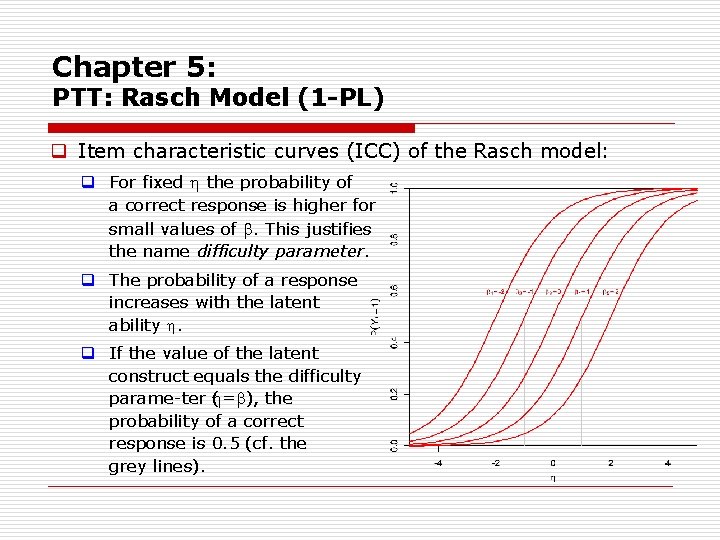
Chapter 5: PTT: Rasch Model (1 -PL) q Item characteristic curves (ICC) of the Rasch model: q For fixed the probability of a correct response is higher for small values of . This justifies the name difficulty parameter. q The probability of a response increases with the latent ability . q If the value of the latent construct equals the difficulty parame ter ( = ), the probability of a correct response is 0. 5 (cf. the grey lines).

Chapter 5: PTT: Rasch Model (1 -PL) q Specific objectivity of the Rasch model: q Logit transformation: Inverse of the logistic function: q It transforms the probabilities back to latent response processes. q The fraction is called odds. q The logarithm of the odds is called logarithmic odds and abbreviated as logit. q The logits are linear functions of both and (see formula above).

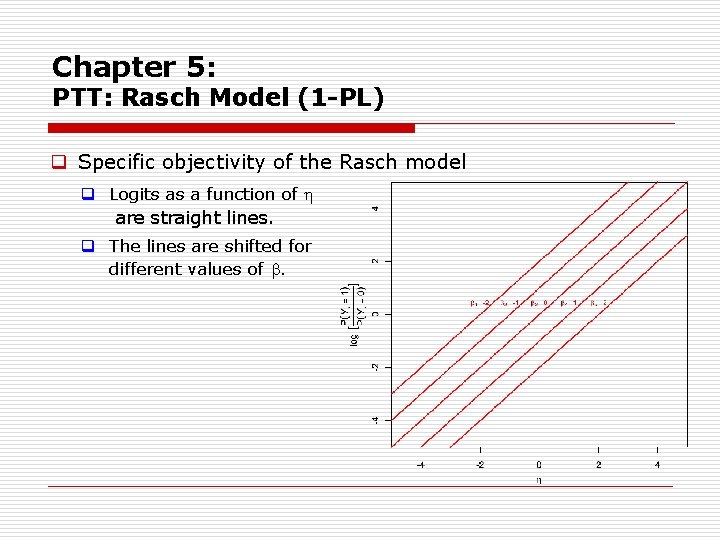
Chapter 5: PTT: Rasch Model (1 -PL) q Specific objectivity of the Rasch model q Logits as a function of are straight lines. q The lines are shifted for different values of .

Chapter 5: PTT: Rasch Model (1 -PL) Concept: Specific objectivity in psychometrics: Refers to two invariant comparisons: (1) Comparisons between examinees are invariant with respect to the test items used to measure them. (2) Comparisons of items are invariant with respect to the examinees used to calibrate them. This means: q For comparing examinees if does not matter which items are used for the comparison. q For com paring items it should be irrelevantwhich examinees these items have been applied to.

Chapter 5: PTT: Rasch Model (1 -PL) q Specific objectivity of the Rasch model: q These two type of invariance hold for the logits in the Rasch model: 1. Invariance of person comparisons: Differences between logits of different participants tested on the same item does not depend on the item used for comparison:

Chapter 5: PTT: Rasch Model (1 -PL) q Specific objectivity of the Rasch model: 2. Invariance of item comparisons: Difference between the logits for two different items i and j, applied to the same participant (or to different participants with the same ability level), does not depend on the value of the ability:

Chapter 5: PTT: Rasch Model (1 -PL) q Specific objectivity of the Rasch model: Can be read off directly from the graphic: 1. Invariance of person comparisons: Consider a single line (item curve). Since the slope of the line is constant the dif ference of the logits depends only on the difference between the ability values but not on the exact location of the ability.

Chapter 5: PTT: Rasch Model (1 -PL) q Specific objectivity of the Rasch model: 2. Invariance of item comparisons: Select two curves. It be comes immediately clear that the vertical separation between the curves is al ways the same, independ ently of the level of ability (= the value on the x axis) chosen. The difference depends only on the separation between the two curves.

Chapter 5: PTT: Rasch Model (1 -PL) Rasch model: Conclusion: q According to the Rasch model item difficulties and persons’ abilities can be placed on the same latent scale. Consequently, the Rasch model enables a comparison of a person’s ability with the difficulty of various test items or with a standard. q Statements are possible about how far the person is located above or below the standard of comparison. q Due to the characteristic of specific objectivity and the possibility of comparing item characteristics (difficulties) with persons’ abilities, a set of test items that conform to the Rasch model represents an ideal measurement instrument for measuring the latent ability construct. q This characteristic is comparable to parallel test items in CTT.

Chapter 5: PTT: 2 -PL Birnbaum model q Extension of the 1 PL model by including an item discrimination parameter i: q The discrimination parameter i affects the slope of the item characte risticcurve (ICC).

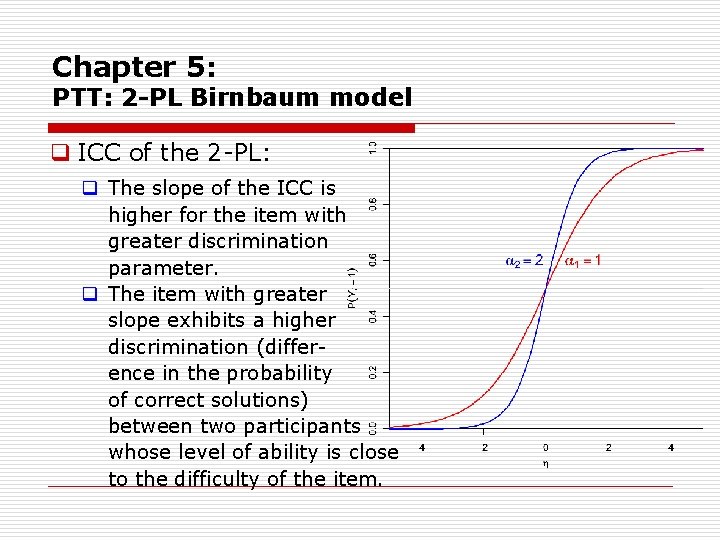
Chapter 5: PTT: 2 -PL Birnbaum model q ICC of the 2 PL: q The slope of the ICC is higher for the item with greater discrimination parameter. q The item with greater slope exhibits a higher discrimination (differ ence in the probability of correct solutions) between two participants whose level of ability is close to the difficulty of the item.

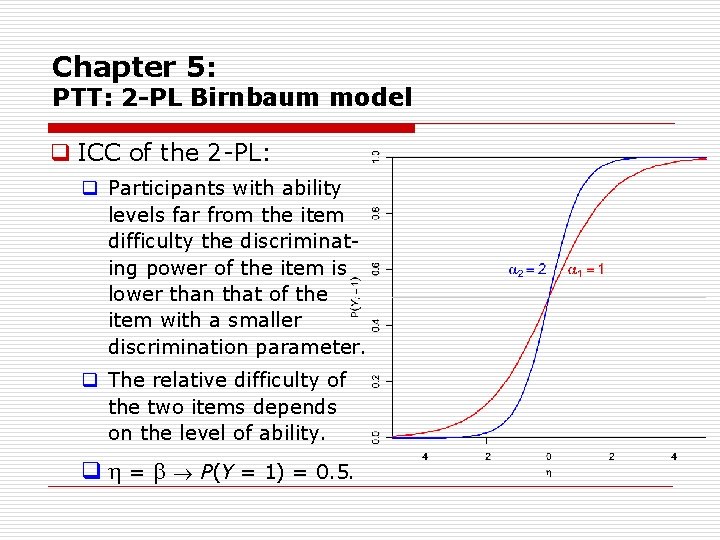
Chapter 5: PTT: 2 -PL Birnbaum model q ICC of the 2 PL: q Participants with ability levels far from the item difficulty the discriminat ing power of the item is lower than that of the item with a smaller discrimination parameter. q The relative difficulty of the two items depends on the level of ability. q = P(Y = 1) = 0. 5.

Chapter 5: PTT: 2 -PL Birnbaum model q 2 -PL model Conclusion: The 2 PL model does not exhibit the nice measurement properties of the Rasch model: q There are no invariant comparisons of items or persons (specific objectivity). q There does not exist a common latent scale on which to locate abilities and items.

Chapter 5: PTT: 3 -PL Birnbaum model q Introduction of a guessing parameter : q According to the model, a correct answer for item i may be achieved by either correct gues sing or by means of a response process that conforms to the 2 PL model.

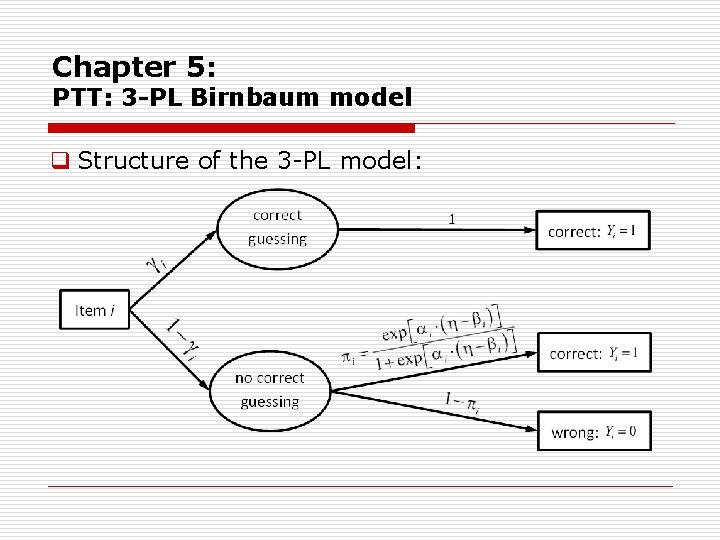
Chapter 5: PTT: 3 -PL Birnbaum model q Structure of the 3 PL model:

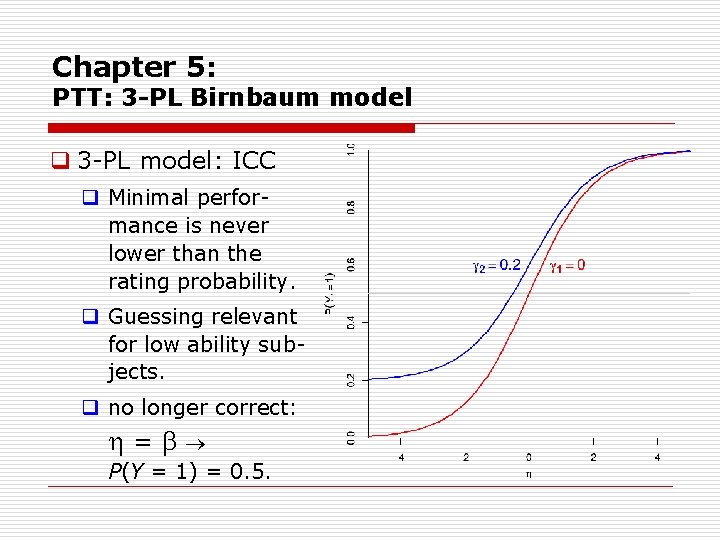
Chapter 5: PTT: 3 -PL Birnbaum model q 3 PL model: ICC q Minimal perfor mance is never lower than the rating probability. q Guessing relevant for low ability sub jects. q no longer correct: = P(Y = 1) = 0. 5.