CHAPTER 5 PARTIAL DERIVATIVES INTRODUCTION SMALL INCREMENTS RATES











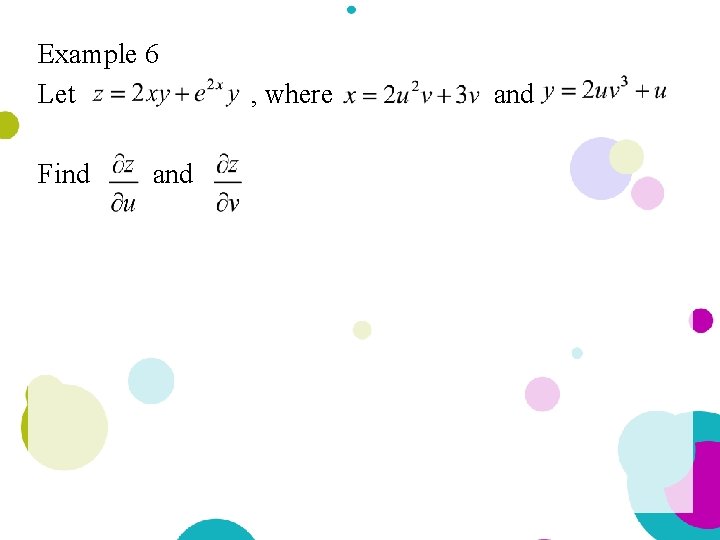




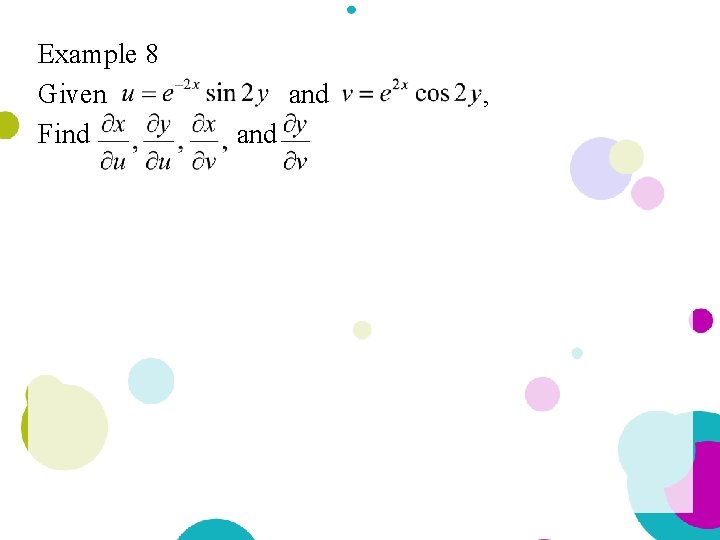
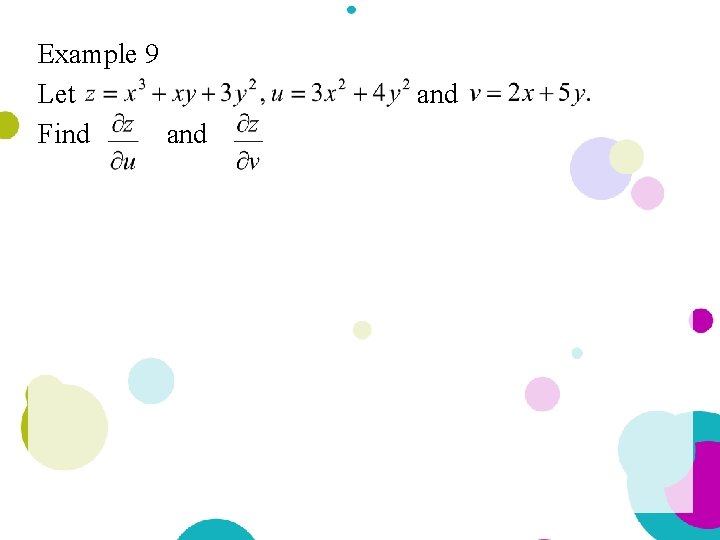





- Slides: 23

CHAPTER 5 PARTIAL DERIVATIVES INTRODUCTION SMALL INCREMENTS & RATES OF CHANGE IMPLICIT FUNCTIONS CHAIN RULE JACOBIAN FUNCTION HESSIAN FUNCTION STATIONARY POINT

INTRODUCTION • Consider the following functions are independent variables. • If we differentiate f with respect variable assume that i. ii. as a single variable as constants where , then we

Notation If • First order partial derivatives: • Second order partial derivatives:

Example 1 Write down all partial derivatives of the following function

Example 2 Write down all partial derivatives of the following functions:

SMALL INCREMENTS & RATES OF CHANGE Notation for small increment is Let then i. A small increment in z, is given by Where are small increments of the stated variables ii. Rate of change z wrt time, t is given by

Example 3 The measurements of closed rectangular box are length, x = 5 m, width y = 3 m, and height, z = 3. 5 m, with a possible error of in each measurement. What is the maximum possible error in the calculated value of the volume, V and the surface, S area of the box?

Example 4 The radius r of a cylinder is increasing at the rate of 0. 2 cms-1 while the height, h is increasing at 0. 5 cms-1. Determine the rate of change for its volume when r=8 cm and h =12 cm.

IMPLICIT FUNCTIONS Definition Let f be a function of two independent variables x and y, given by constant. To determine the derivative of this implicit function: Let Hence,

Example 5 Assume that y is a differentiable of x that satisfies the given function. Find using implicit differentiation.

THE CHAIN RULE Definition Let z be a function of two independent variables x and y, while x and y are functions of two independent variables u and v. The derivatives of z with respect to u and v as follows: Hence,
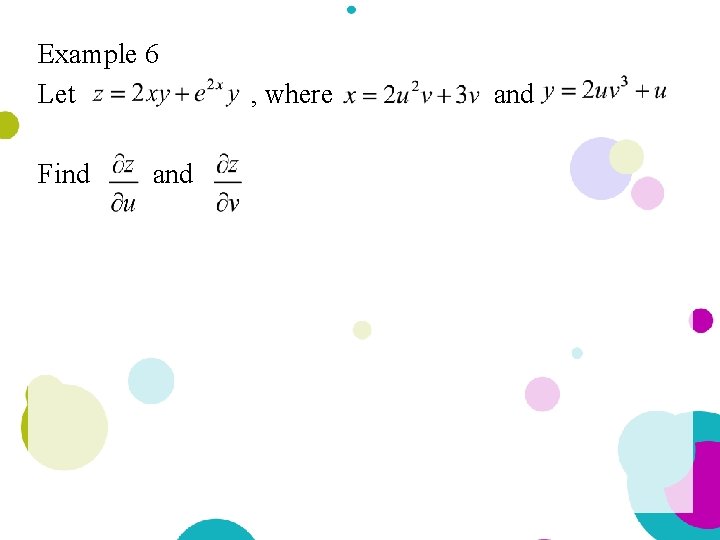
Example 6 Let Find and , where and

JACOBIAN FUNCTION Definition Let be n number of functions of n variables

JACOBIAN FUNCTION Jacobian for this system of equations is given by: OR

Example 7 Given and Jacobian for the system of equation. , determine the

INVERSE FUNCTIONS FOR PARTIAL DERIVATIVES Definition Let u and v be two functions of two independent variables x and y. . . Partial derivatives and are given by:
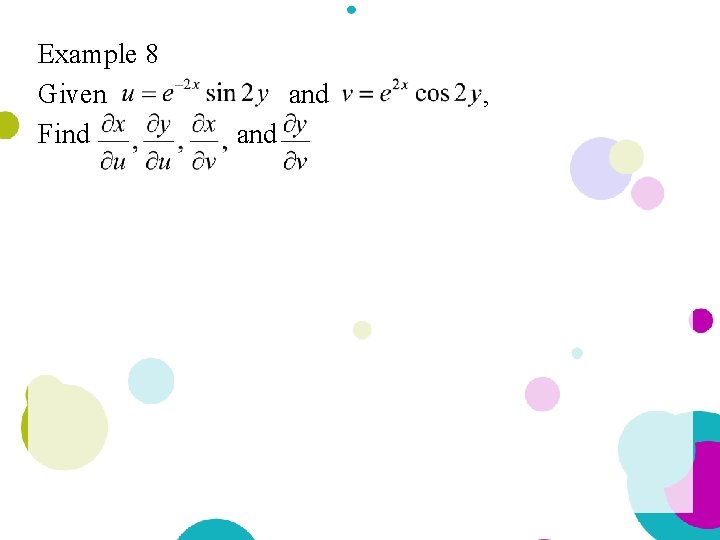
Example 8 Given Find and ,
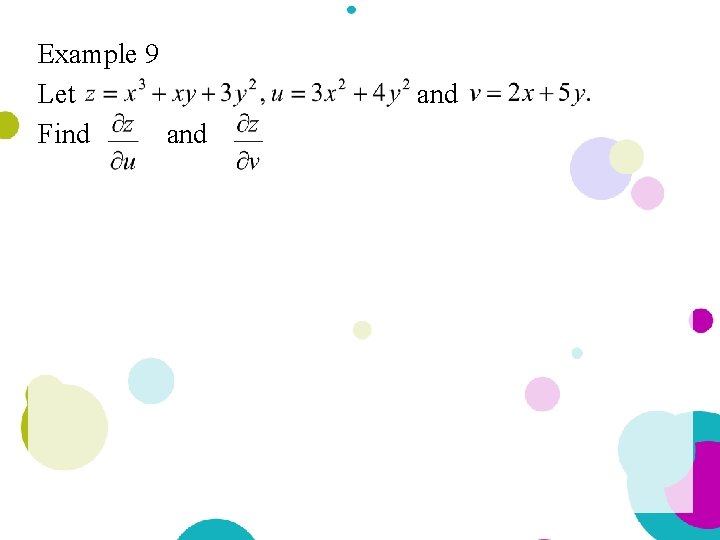
Example 9 Let Find and

HESSIAN FUNCTION Definition Let f be a function of n number of variables Hessian of f is given by the following determinant: .

HESSIAN FUNCTION Hessian of a function of 2 variables: Let f be a function of 2 independent variables x and y. Then the Hessian of f is given by:

HESSIAN FUNCTION Stationary Point Definition Given a function occurs when . The stationary point of and Properties of Stationary Point

HESSIAN FUNCTION Properties of Stationary Point a) If H<0, then stationary point is a SADDLE POINT b) If H>0 a) MAXIMUM POINT if b) MINIMUM POINT if c) If H=0, then TEST FAILS or NO CONCLUSION

Example 10 Find and classify the stationary points of