Chapter 5 Numerical Integration 1 A Review of















































- Slides: 57

Chapter 5 Numerical Integration 1

A Review of the Definite Integral 2

Riemann Sum p A summation of the form is called a Riemann sum. 3

5. 2 Improving the Trapezoid Rule p The trapezoid rule for computing integrals: p The error: 4

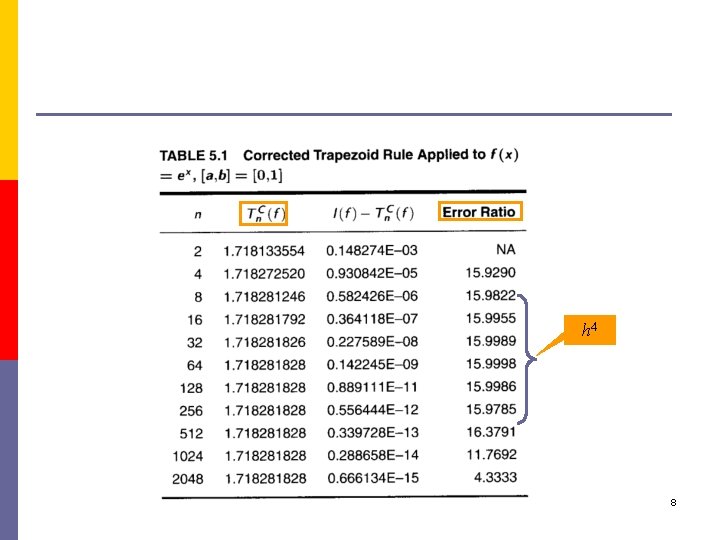
5. 2 Improving the Trapezoid Rule p So that p Therefore, p Error estimation: p Improvement of the approximation: the corrected trapezoid rule 5

Example 5. 1 6

Example 5. 2 7

h 4 8

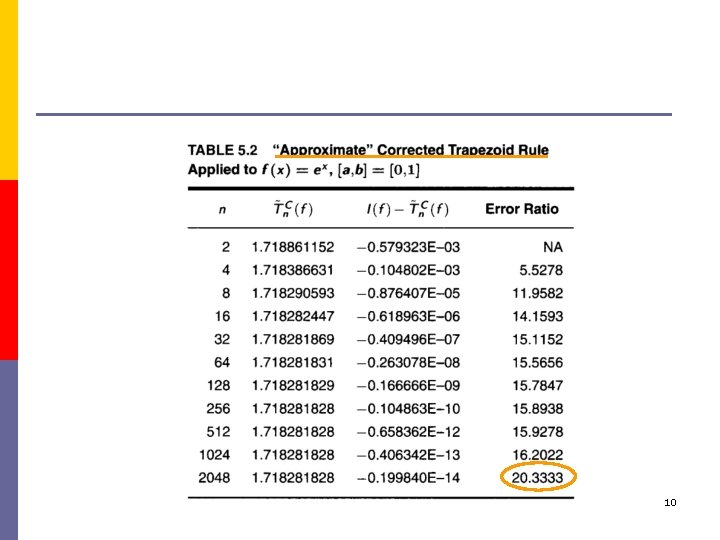
Approximate Corrected Trapezoid Rule 9

10

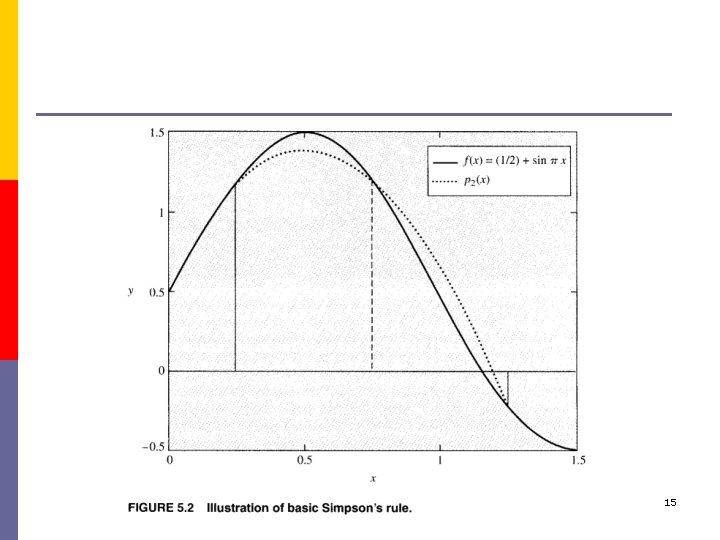
5. 3 Simpson’s Rule and Degree of Precision 11

let 12

13

Example 5. 3 14

15

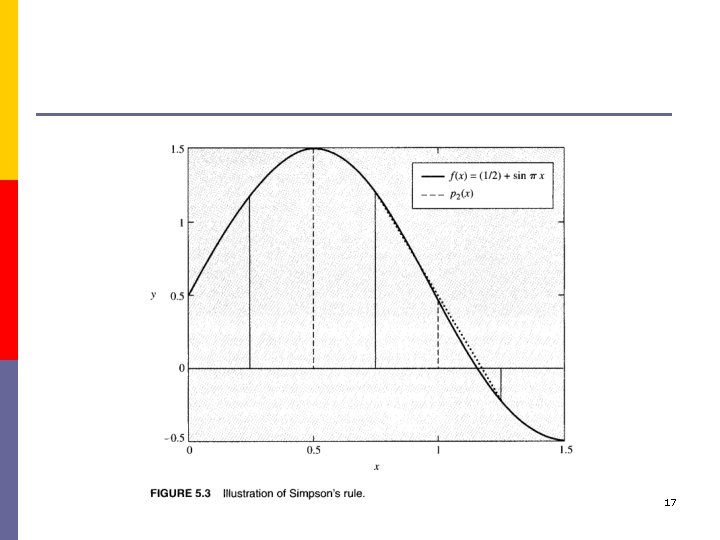
The Composite Rule Assume Example 5. 4 16

17

Example 5. 5 h 4 It’s OK!! 18

Discussion p From our experiments: p From the definition of Simpson’s rule: p Why? Why Simpson’s rule is “more accurate than it ought to be”? 19

20

21

22

23

Example 5. 6 24

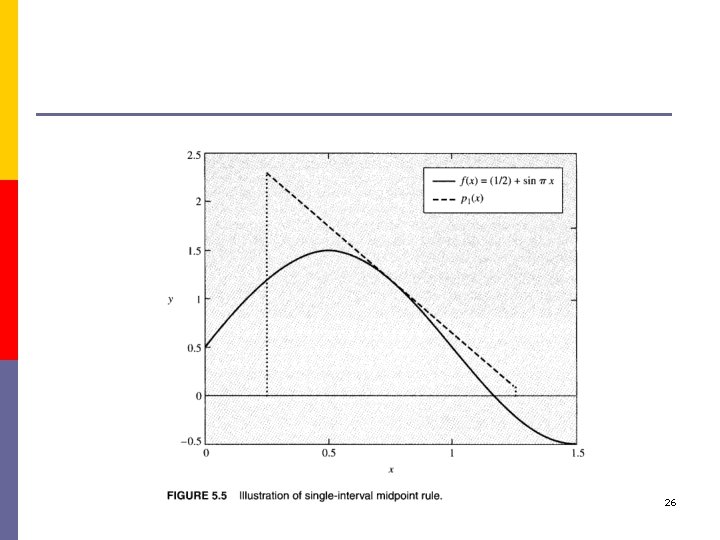
5. 4 The Midpoint Rule p Consider the integral: p And the Taylor approximation: p The midpoint rule: p Its composite rule: because 25

26

27

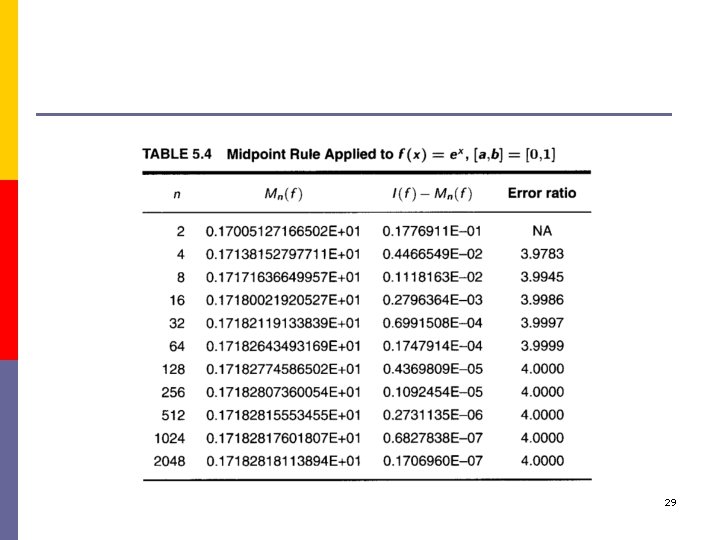
Example 5. 7 28

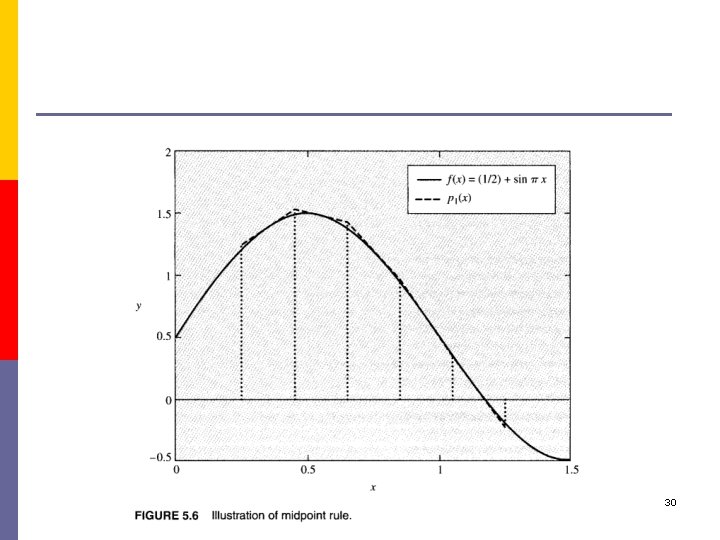
29

30

5. 5 Application: Stirling’s Formula p Stirling’s formula is an interesting and useful way to approximate the factorial function, n!, for large values of n. Example Use Stirling’s formula to show that for all x. 31

5. 6 Gaussian Quadrature p p p Gaussian quadrature is a very powerful tool for approximating integrals. The quadrature rules are all base on special values of weights and abscissas (called Gauss points) The quadrature rule is written in the form weights Gauss points 32

33

Example 5. 8 34

Question × k 35

Discussion p The high accuracy of Gaussian quadrature then comes from the fact that it integrates very-high-degree polynomials exactly. p We should choose N=2 n-1, because a polynomial of degree 2 n-1 has 2 n coefficients, and thus the number of unknowns (n weights plus n abscissas) equals the number of equations. p Taking N=2 n will yield a contradiction. 36

Only to find an example 37

38

Finding Gauss Points 39

Theorem 5. 3 40

Theorem 5. 4 41

42

Other Intervals, Other Rules 43

Example 5. 9 Table 5. 5 44

Error estimation!! See exercise!! 45

Example 5. 10 46

47

5. 7 Extrapolation Methods p One of the most important ideas in computational mathematics is— n n p We can take the information from a few approximations and Use that to both estimate the error in the approximation and generate a significantly improved approximation In this section we will embark on a more detailed study of some of these ideas. 48

Approximation 49

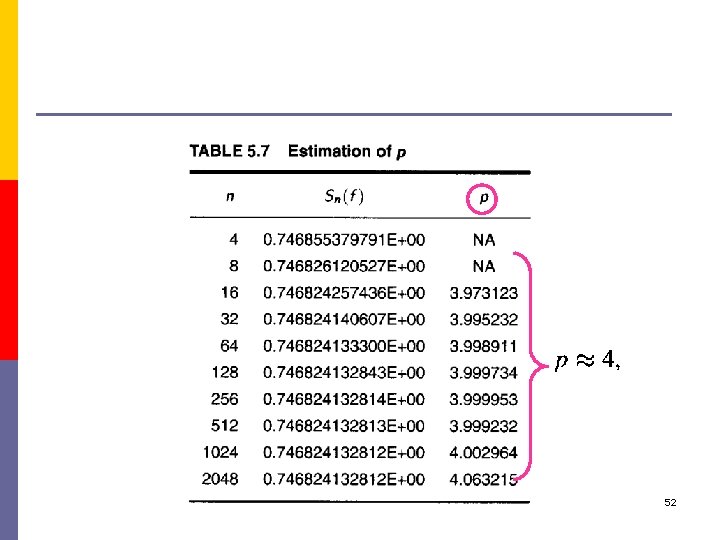
Estimating p 50

Example 5. 11 51

52

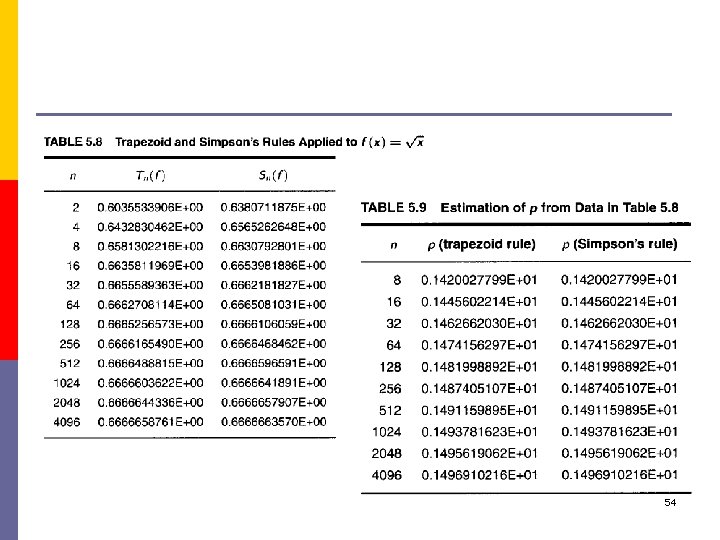
Example 5. 12 53

54

Error Estimation and an Improved Approximation I 2 n-In 55

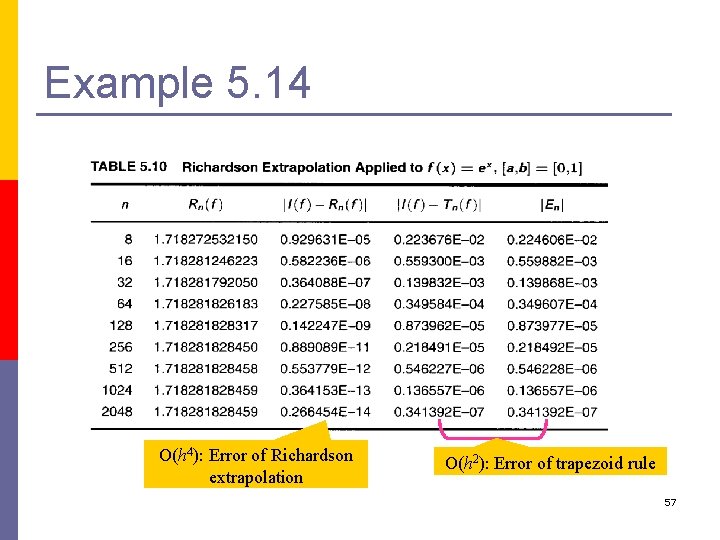
Example 5. 13 56

Example 5. 14 O(h 4): Error of Richardson extrapolation O(h 2): Error of trapezoid rule 57