Chapter 5 Normal Probability Distributions Section 5 3

Chapter 5 Normal Probability Distributions Section 5 -3 – Normal Distributions: Finding Values A. We have learned how to calculate the probability given an x-value or a z-score. In this lesson, we will explore how to find an x-value or z-score when given the probability (cumulative area under the curve). 1. The cumulative area under the curve is a direct variation of the zscore; as the z-score goes up, so does the cumulative area. a. Because this is a one to one function, it also has an inverse function. 1) Lucky for us, the calculator has an operation to find the inverse of the cumulative area. a) 2 nd VARS inv. Norm(probability, 0, 1) = z-score. b) 2 nd VARS inv. Norm(probability, mean, s. d. ) = x-value

Chapter 5 Normal Probability Distributions Section 5 -3 – Normal Distributions: Finding Values B. The key here is going to be using the correct area under the curve to find the z or x value that we are looking for. 1. Practice will make this a LOT easier. a. As a general rule, if we want the area BELOW a given percentile, we use the given percentile. b. If we want the area ABOVE a given percentile, we subtract the given percentile from 1 and use the answer. (Complement Rule)

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 1 – Page 261 1. Find the z-score that corresponds to a cumulative area of 0. 3632 0. 0015 0. 0215 0. 023 0. 136 0. 159 0. 341 0. 500 0. 341 0. 841 0. 136 0. 0215 0. 977 0. 0015 0. 9985 Since. 3632 is between. 159 and. 500, the answer MUST be between -1 and 0. 2 nd VARS 3 (. 3632, 0, 1) = -. 3499.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 1 – Page 261 1. Find the z-score that corresponds to a cumulative area of 0. 3632 0. 0015 0. 0215 0. 023 0. 136 0. 159 0. 341 0. 500 0. 341 0. 841 0. 136 0. 0215 0. 977 0. 0015 0. 9985 You can check this answer using what we learned in Section 5 -1. Normalcdf of -. 3499 should give us an area of. 3632. If it doesn’t, something is wrong. Check it again. 2 nd VARS 2 (-1 E 99, -. 3499, 0, 1) =. 3632, so we are correct.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 1 – Page 261 2. Find the z-score that has 10. 75% of the distribution to its right. 0. 0015 0. 0215 0. 023 0. 136 0. 159 0. 341 0. 500 0. 341 0. 841 0. 136 0. 0215 0. 977 0. 0015 0. 9985 If it has. 1075 to the right, then it has. 8925 to the left (1 -. 1075 =. 8925) Since. 8925 is between. 841 and. 977, the answer is between 1 and 2. 2 nd VARS 3 (. 8925, 0 , 1) = 1. 2399 2 nd VARS 2 (1. 2399, 1 E 99, 0, 1) =. 1075, so we are correct.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 2 – Page 262 Find the z-score that corresponds to each percentile. 1) P 5 2) P 50 3) P 90

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 2 – Page 262 Find the z-score that corresponds to each percentile. 1) P 5 0. 0015 0. 0215 0. 023 0. 136 0. 159 0. 341 0. 500 0. 341 0. 841 0. 136 0. 0215 0. 977 0. 0015 0. 9985 Since. 05 is between. 023 and. 159, the answer is between -2 and -1. 2 nd VARS 3 (. 05, 0, 1) = -1. 645. 2 nd VARS 2 (-1 E 99, -1. 645, 0, 1) =. 04998, which is close enough to. 05. We know we are right, since it checked.

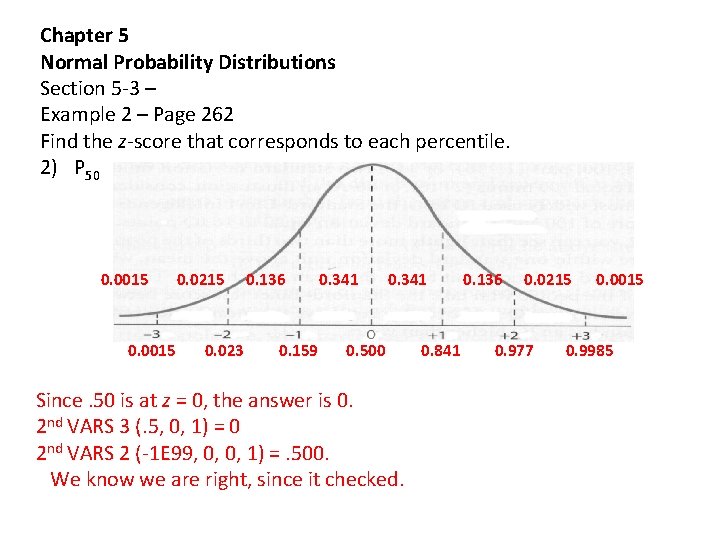
Chapter 5 Normal Probability Distributions Section 5 -3 – Example 2 – Page 262 Find the z-score that corresponds to each percentile. 2) P 50 0. 0015 0. 0215 0. 023 0. 136 0. 159 0. 341 0. 500 Since. 50 is at z = 0, the answer is 0. 2 nd VARS 3 (. 5, 0, 1) = 0 2 nd VARS 2 (-1 E 99, 0, 0, 1) =. 500. We know we are right, since it checked. 0. 841 0. 136 0. 0215 0. 977 0. 0015 0. 9985

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 2 – Page 262 Find the z-score that corresponds to each percentile. 3) P 90 0. 0015 0. 0215 0. 023 0. 136 0. 159 0. 341 0. 500 0. 341 0. 841 0. 136 0. 0215 0. 977 0. 0015 0. 9985 Since. 90 is between. 841 and. 977, the answer is between 1 and 2 2 nd VARS 3 (. 9, 0, 1) = 1. 282 2 nd VARS 2 (-1 E 99, 1. 282, 0, 1) =. 90008, which is close enough to. 9. We know we are right, since it checked.

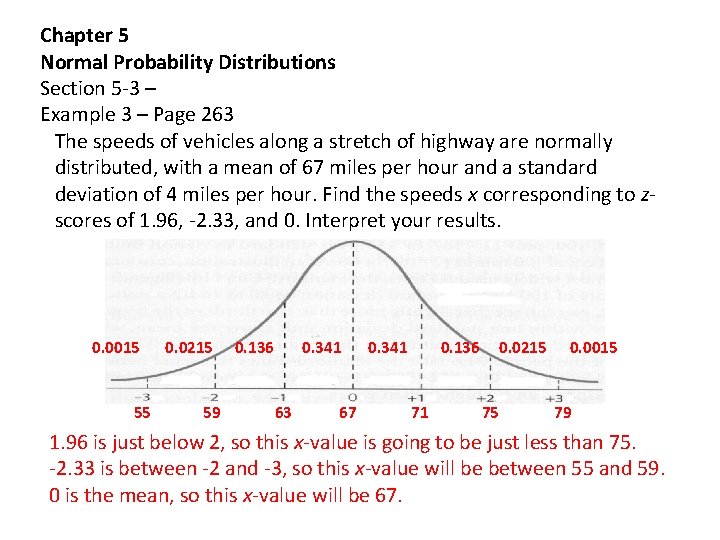
Chapter 5 Normal Probability Distributions Section 5 -3 – Example 3 – Page 263 The speeds of vehicles along a stretch of highway are normally distributed, with a mean of 67 miles per hour and a standard deviation of 4 miles per hour. Find the speeds x corresponding to zscores of 1. 96, -2. 33, and 0. Interpret your results. 0. 0015 55 0. 0215 59 0. 136 0. 341 63 67 0. 341 0. 136 71 0. 0215 75 0. 0015 79 1. 96 is just below 2, so this x-value is going to be just less than 75. -2. 33 is between -2 and -3, so this x-value will be between 55 and 59. 0 is the mean, so this x-value will be 67.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 3 – Page 263 The speeds of vehicles along a stretch of highway are normally distributed, with a mean of 67 miles per hour and a standard deviation of 4 miles per hour. Find the speeds x corresponding to zscores of 1. 96, -2. 33, and 0. Interpret your results.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 4 – Page 264 Scores for a civil service exam are normally distributed with a mean of 75 and a standard deviation of 6. 5. To be eligible for civil service employment, you must score in the top 5%. What is the lowest score you can earn and still be eligible for employment? Inv. Norm(. 05, 0, 1) = -1. 645 0. 0015 0. 0215 0. 136 0. 341 Inv. Norm(. 50, 0, 1) = 0. 000 0. 0015 0. 023 0. 159 0. 500 75 0. 341 0. 841 81. 5 0. 136 0. 0215 0. 977 88 0. 0015 0. 9985 94. 5 To be in the top 5%, you must beat 95% (. 95) of the people taking the test. . 95 falls between 81. 5 and 88, so your answer must be in that range.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 4 – Page 264 Scores for a civil service exam are normally distributed with a mean of 75 and a standard deviation of 6. 5. To be eligible for civil service employment, you must score in the top 5%. What is the lowest score you can earn and still be eligible for employment? 2 nd VARS 3 (. 95, 75, 6. 5) = 85. 692 You need at least an 86 to be eligible for civil service employment. This fits with our guess of between 81. 5 and 88, so we can be satisfied that we are correct. We can also check this answer using the normal distribution. 2 nd VARS 2 (86, 1 E 99, 75, 6. 5) =. 045, which puts you in the top 5%, so it checks. Notice that if you used 85 as your score, you are only in the top 6. 2%, and therefore not eligible for employment.

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 5 – Page 265 In a randomly selected sample of 1169 men ages 35 -44, the mean total cholesterol level was 210 milligrams per deciliter with a standard deviation of 38. 6 milligrams per deciliter. Assume the total cholesterol levels are normally distributed. Find the highest total cholesterol level a man in this 35 -44 age group can have and be in the lowest 1%. You want the x-value that corresponds to the area of 1%. Remember that to find a score below the given percentile, you use that percentile.

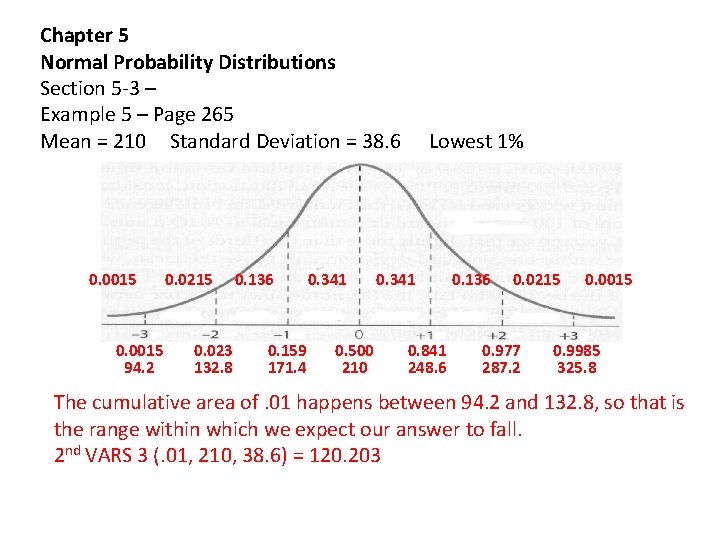
Chapter 5 Normal Probability Distributions Section 5 -3 – Example 5 – Page 265 Mean = 210 Standard Deviation = 38. 6 Lowest 1% Inv. Norm(. 05, 0, 1) = -1. 645 0. 0015 0. 0215 0. 136 0. 341 0. 136 0. 0215 0. 0015 Inv. Norm(. 50, 0, 1) = 0. 000 0. 0015 94. 2 0. 023 132. 8 0. 159 171. 4 0. 500 210 0. 841 248. 6 0. 977 287. 2 0. 9985 325. 8 The cumulative area of. 01 happens between 94. 2 and 132. 8, so that is the range within which we expect our answer to fall. 2 nd VARS 3 (. 01, 210, 38. 6) = 120. 203

Chapter 5 Normal Probability Distributions Section 5 -3 – Example 5 – Page 265 In a randomly selected sample of 1169 men ages 35 -44, the mean total cholesterol level was 210 milligrams per deciliter with a standard deviation of 38. 6 milligrams per deciliter. Assume the total cholesterol levels are normally distributed. Find the highest total cholesterol level a man in this 35 -44 age group can have and be in the lowest 1%. The answer of 120 fits inside our expected range of between 94. 2 and 132. 8, so we can accept it as possibly correct. Again, we can check this answer. 2 nd VARS 2 (-1 E 99, 120, 210, 38. 6) =. 009, which rounds to. 01. A 35 -44 year old man needs a cholesterol level of 120 or less to be in the lowest 1% for his age group.

Your Assignments are: Classwork: Pages 266– 267 #2– 38 Evens Homework: Pages 267– 268 #39 -46 All