Chapter 5 Normal Probability Distributions Overview The Standard

Chapter 5 Normal Probability Distributions Overview The Standard Normal Distributions: Finding Probabilities Normal Distributions: Finding Values The Central Limit Theorem 1

Definition Standard Normal Deviation a normal probability distribution that has a mean of 0 and a standard deviation of 1 2
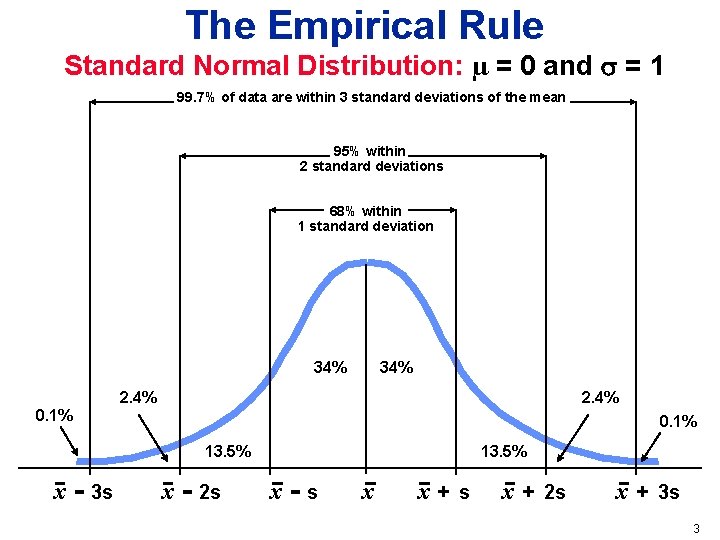
The Empirical Rule Standard Normal Distribution: µ = 0 and = 1 99. 7% of data are within 3 standard deviations of the mean 95% within 2 standard deviations 68% within 1 standard deviation 34% 2. 4% 0. 1% 13. 5% x - 3 s x - 2 s 13. 5% x-s x x+s x + 2 s x + 3 s 3
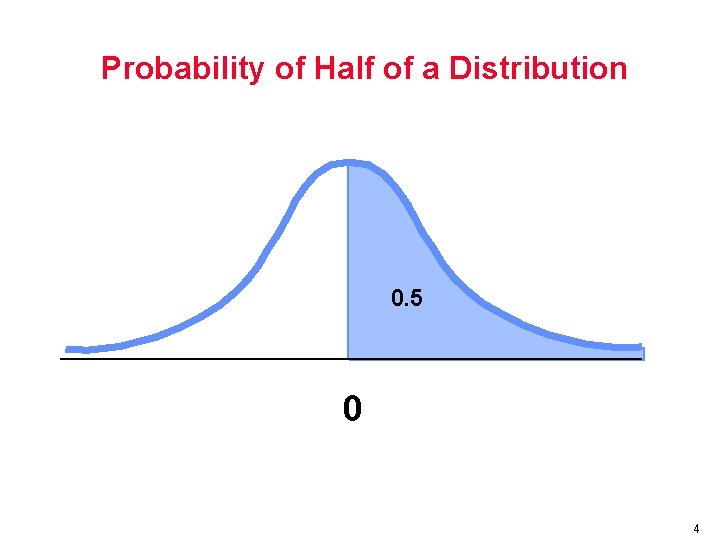
Probability of Half of a Distribution 0. 5 0 4

Notation P(a < z < b) denotes the probability that the z score is between a and b P(z > a) denotes the probability that the z score is greater than a P (z < a) denotes the probability that the z score is less than a 5
=1 µ=0 0 x z 6

Finding a probability when given a z-score using the TI 83/84 • • 2 nd Distributions 2: normalcdf (lower bound, upper bound, mean, s. d. ) 7
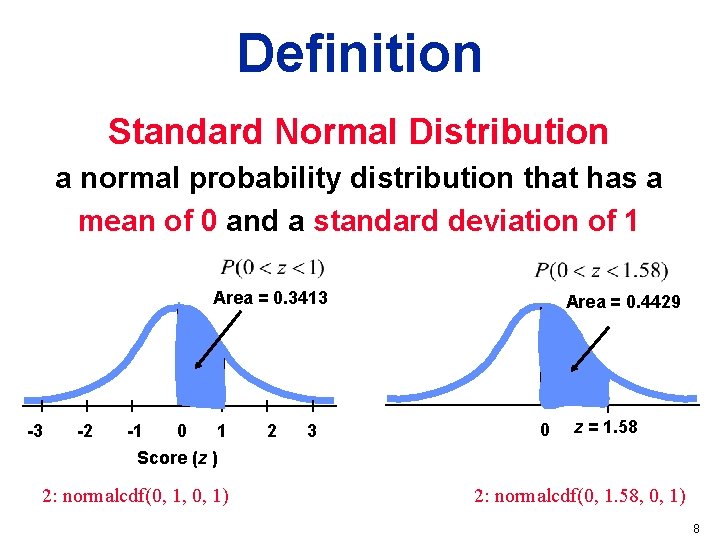
Definition Standard Normal Distribution a normal probability distribution that has a mean of 0 and a standard deviation of 1 Area = 0. 3413 -3 -2 -1 0 1 Score (z ) 2: normalcdf(0, 1, 0, 1) 2 3 Area = 0. 4429 0 z = 1. 58 2: normalcdf(0, 1. 58, 0, 1) 8

Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1. 58 degrees. 2: normalcdf (0, 1. 58, 0, 1) 9
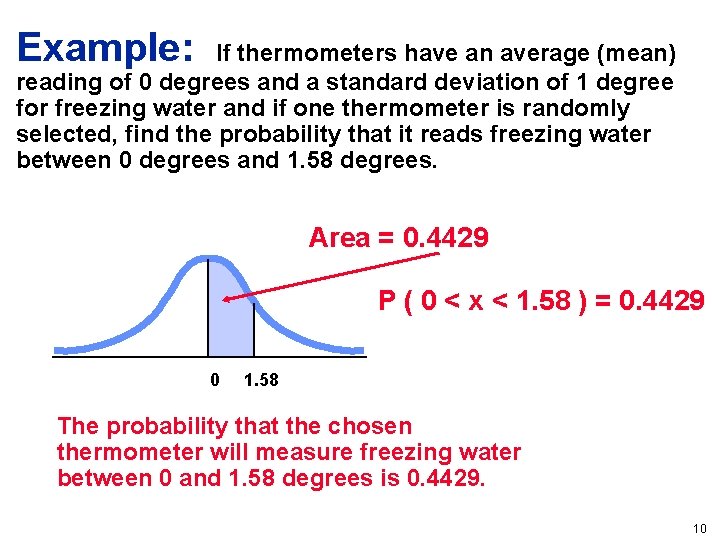
Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water and if one thermometer is randomly selected, find the probability that it reads freezing water between 0 degrees and 1. 58 degrees. Area = 0. 4429 P ( 0 < x < 1. 58 ) = 0. 4429 0 1. 58 The probability that the chosen thermometer will measure freezing water between 0 and 1. 58 degrees is 0. 4429. 10

Example: If thermometers have an average (mean) reading of 0 degrees and a standard deviation of 1 degree for freezing water, and if one thermometer is randomly selected, find the probability that it reads freezing water between -2. 43 degrees and 0 degrees. 2: normalcdf(-2. 43, 0, 0, 1) Area = 0. 4925 P ( -2. 43 < x < 0 ) = 0. 4925 -2. 43 0 The probability that the chosen thermometer will measure freezing water between -2. 43 and 0 degrees is 0. 4925. 11
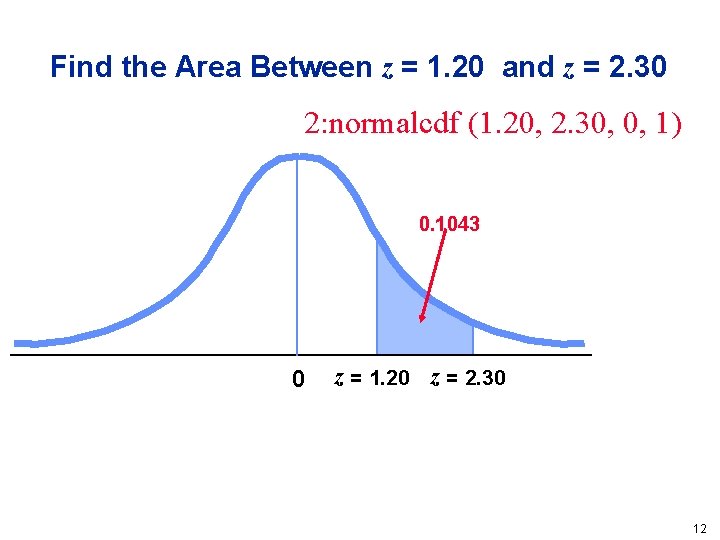
Find the Area Between z = 1. 20 and z = 2. 30 2: normalcdf (1. 20, 2. 30, 0, 1) 0. 1043 0 z = 1. 20 z = 2. 30 12
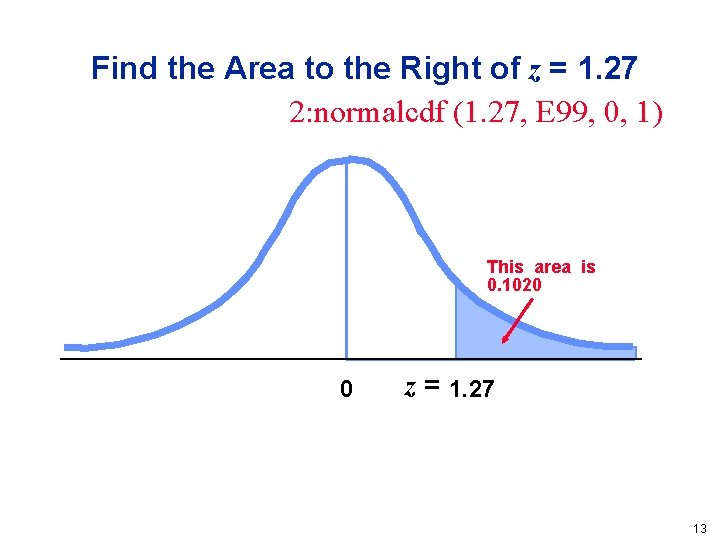
Find the Area to the Right of z = 1. 27 2: normalcdf (1. 27, E 99, 0, 1) This area is 0. 1020 0 z = 1. 27 13
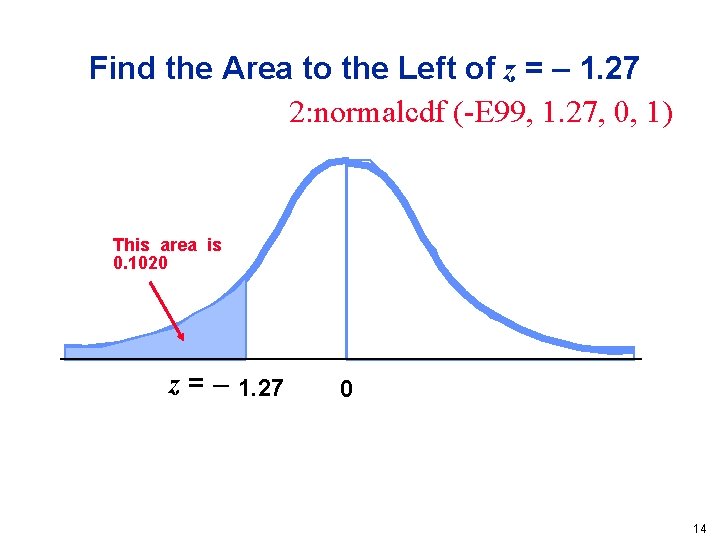
Find the Area to the Left of z = – 1. 27 2: normalcdf (-E 99, 1. 27, 0, 1) This area is 0. 1020 z = – 1. 27 0 14

Other Normal Distributions 0 1 If or (or both), we will convert values to standard scores using Formula 5 -2, then procedures for working with all normal distributions are the same as those for the standard normal distribution. z= x-µ 15

Converting to Standard Normal Distribution P (a) x 16
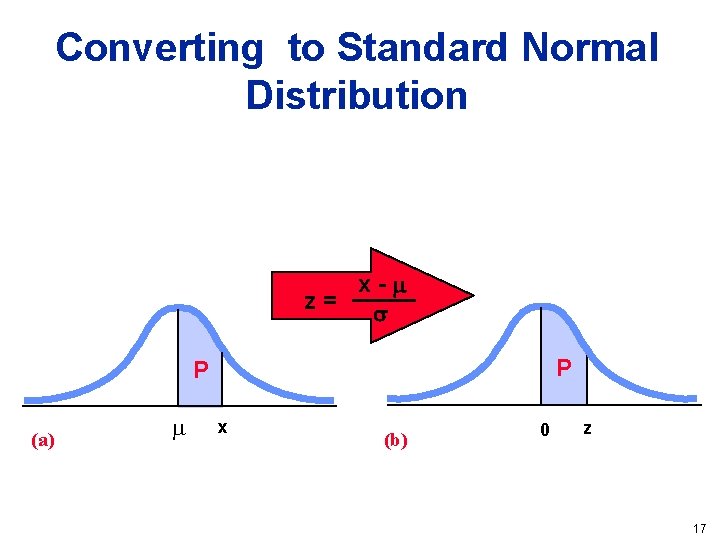
Converting to Standard Normal Distribution x- z= P P (a) x (b) 0 z 17
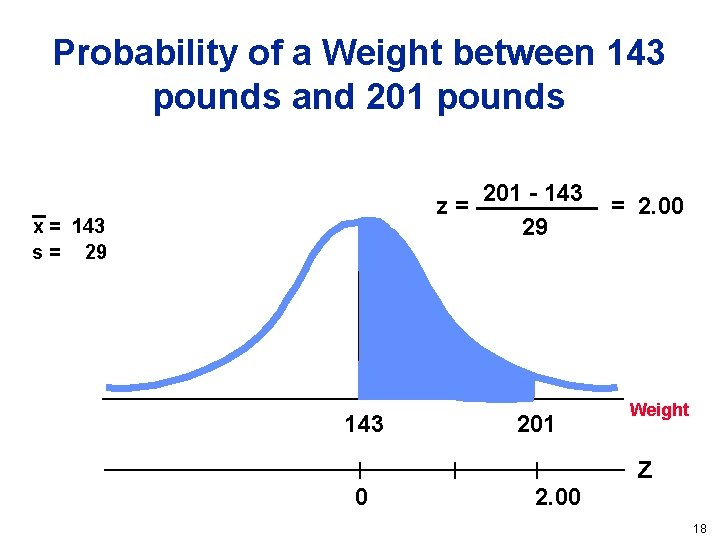
Probability of a Weight between 143 pounds and 201 pounds z= x = 143 s = 29 143 0 201 - 143 29 201 2. 00 = 2. 00 Weight z 18
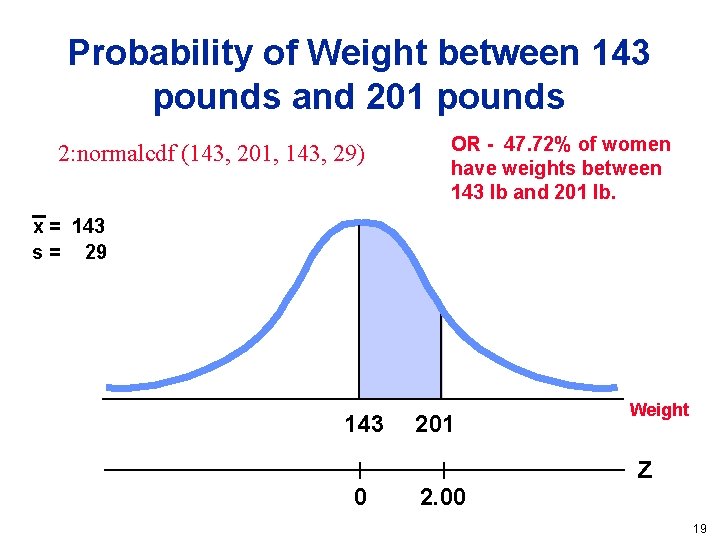
Probability of Weight between 143 pounds and 201 pounds 2: normalcdf (143, 201, 143, 29) OR - 47. 72% of women have weights between 143 lb and 201 lb. x = 143 s = 29 143 0 201 2. 00 Weight z 19

Definition Sampling Distribution of the mean the probability distribution of sample means, with all samples having the sample size n. 20

Central Limit Theorem Given: 1. The random variable x has a distribution (which may or may not be normal) with mean µ and standard deviation . 2. Samples all of the same size n are randomly selected from the population of x values. 21

Notation the mean of the sample means µx = µ the standard deviation of sample mean x = n (often called standard error of the mean) 22

Finding a z - score for a group Using TI 83 • • 2 nd Distributions 2: normalcdf (lower bound, upper bound, mean, s. e) – Replace s. d. with standard error 23

Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a. ) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. b. ) if 36 different women are randomly selected, find the probability that their mean weight is greater than 150 lb. 24
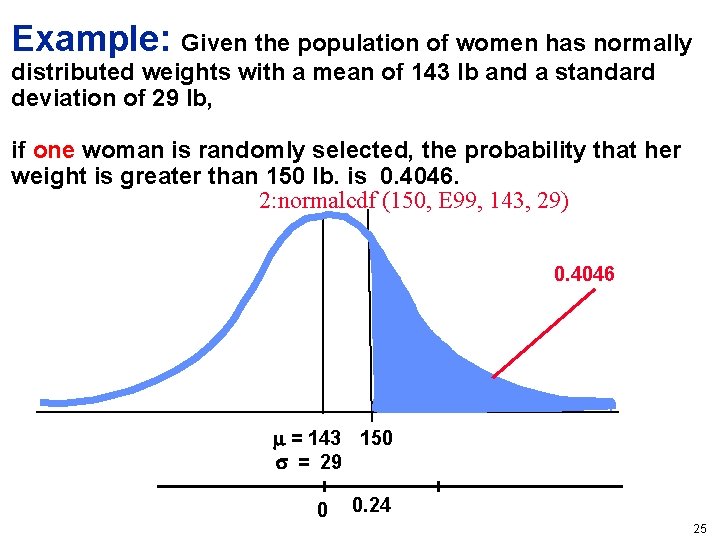
Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, if one woman is randomly selected, the probability that her weight is greater than 150 lb. is 0. 4046. 2: normalcdf (150, E 99, 143, 29) 0. 4046 = 143 150 = 29 0 0. 24 25
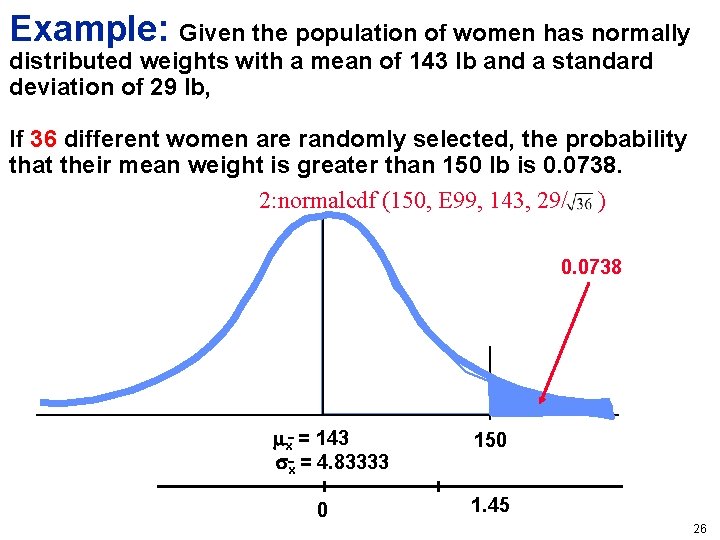
Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, If 36 different women are randomly selected, the probability that their mean weight is greater than 150 lb is 0. 0738. 2: normalcdf (150, E 99, 143, 29/ ) 0. 0738 x = 143 x = 4. 83333 0 150 1. 45 26
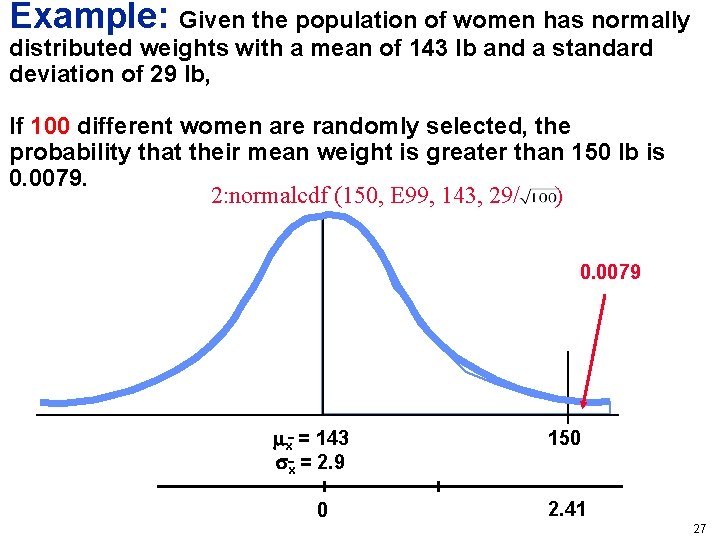
Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, If 100 different women are randomly selected, the probability that their mean weight is greater than 150 lb is 0. 0079. 2: normalcdf (150, E 99, 143, 29/ ) 0. 0079 x = 143 x = 2. 9 0 150 2. 41 27

Example: Given the population of women has normally distributed weights with a mean of 143 lb and a standard deviation of 29 lb, a. ) if one woman is randomly selected, find the probability that her weight is greater than 150 lb. P(x > 150) = 0. 4052 b. ) if 36 different women are randomly selected, their mean weight is greater than 150 lb. P(x > 150) = 0. 0735 c. ) if 100 different women are randomly selected, their mean weight is greater than 150 lb. P(x > 150) = 0. 0079 It is much easier for an individual to deviate from the mean than it is for a group of 36 or 100 to deviate from the mean. 28

Finding z Scores when Given Probabilities Using the TI 83 • • 2 nd Distributions 3: Invnorm (%, mean, s. d) 29
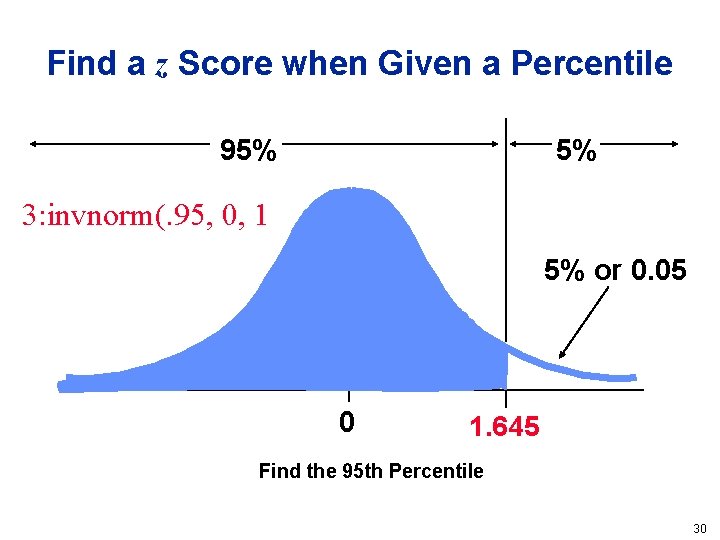
Find a z Score when Given a Percentile 95% 5% 3: invnorm(. 95, 0, 1 5% or 0. 05 0 1. 645 Find the 95 th Percentile 30
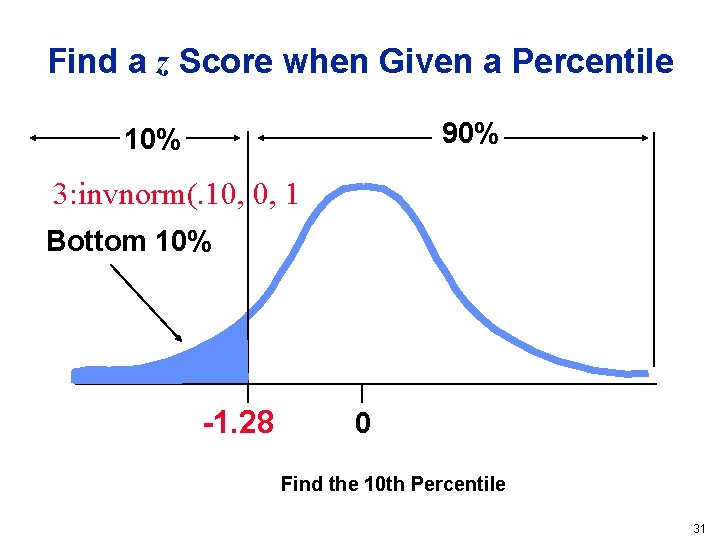
Find a z Score when Given a Percentile 90% 10% 3: invnorm(. 10, 0, 1 Bottom 10% -1. 28 0 Find the 10 th Percentile 31
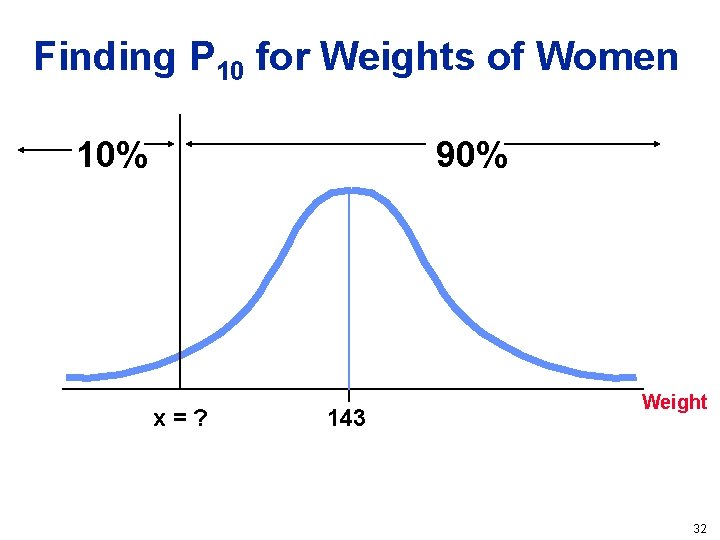
Finding P 10 for Weights of Women 10% 90% x=? 143 Weight 32
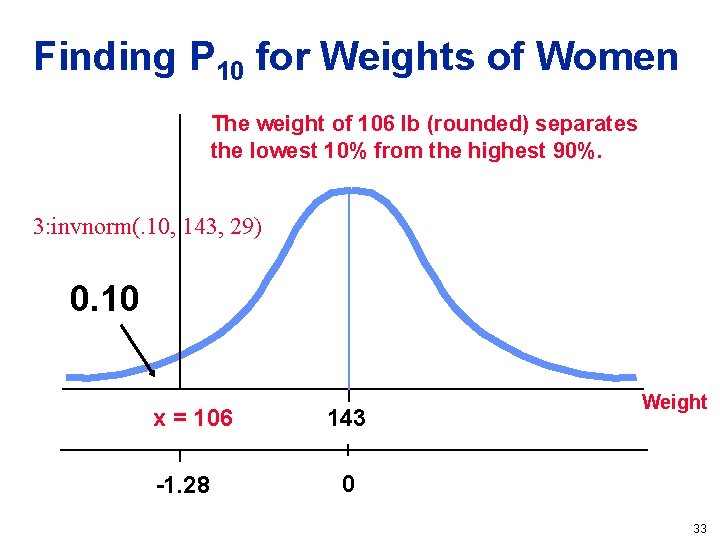
Finding P 10 for Weights of Women The weight of 106 lb (rounded) separates the lowest 10% from the highest 90%. 3: invnorm(. 10, 143, 29) 0. 10 x = 106 -1. 28 143 Weight 0 33
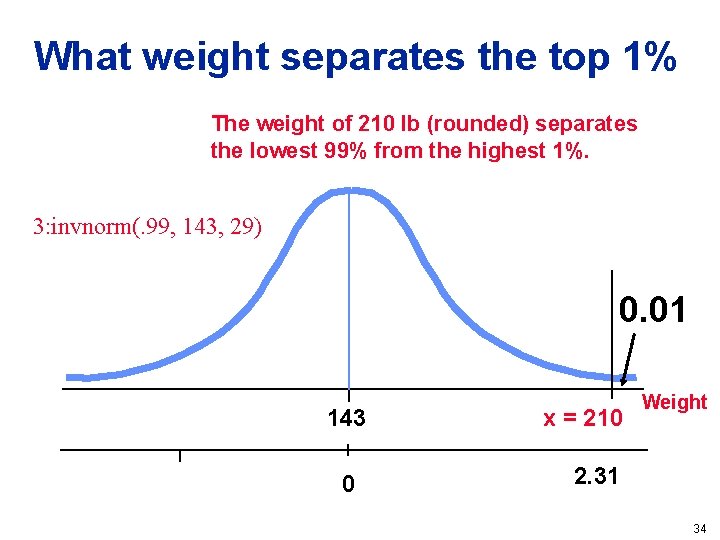
What weight separates the top 1% The weight of 210 lb (rounded) separates the lowest 99% from the highest 1%. 3: invnorm(. 99, 143, 29) 0. 01 143 0 x = 210 Weight 2. 31 34
- Slides: 34