Chapter 5 Nonlinear Programming Chemical Engineering Department National

Chapter 5 Nonlinear Programming Chemical Engineering Department National Tsing-Hua University Prof. Shi-Shang Jang May, 2003 1

Problem Statement 2

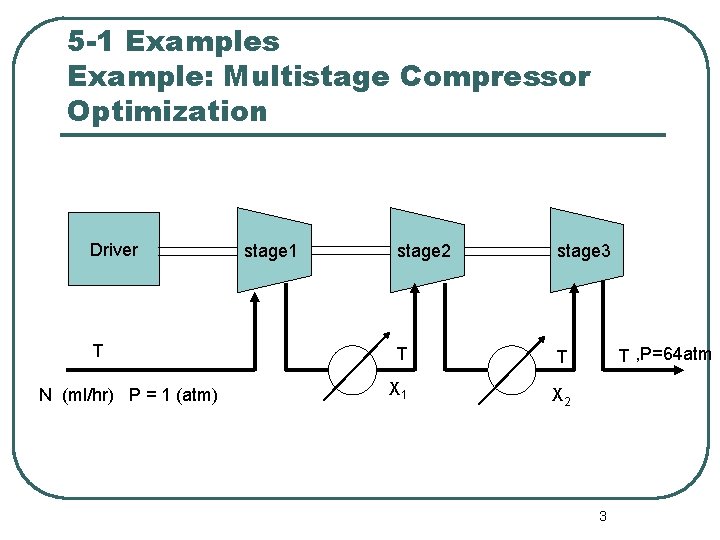
5 -1 Examples Example: Multistage Compressor Optimization Driver T N (ml/hr) P = 1 (atm) stage 1 stage 2 stage 3 T T X 1 X 2 T , P=64 atm 3

Example: Multistage Compressor Optimization 4

Example: Multistage Compressor Optimization 5

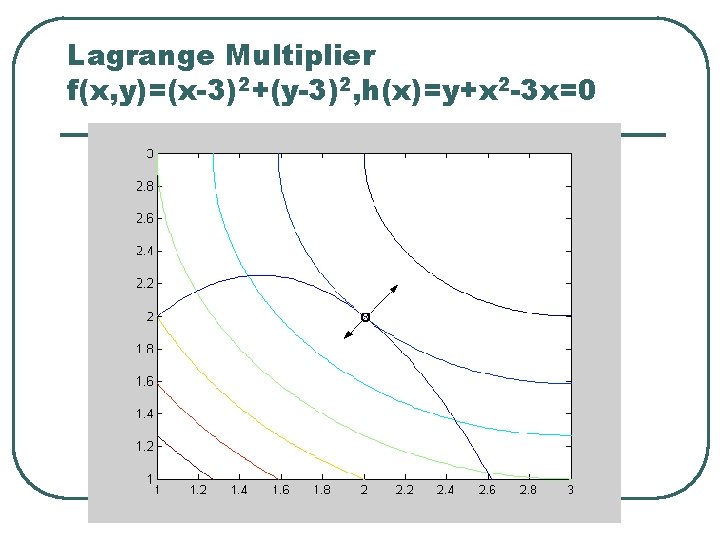
5 -3 Lagrange Multiplier 6

Lagrange Multiplier f(x, y)=(x-3)2+(y-3)2, h(x)=y+x 2 -3 x=0 7

Solution 8

Physical Meaning of Lagrange Multiplier – Shadow Price 9

5 -4 Kuhn-Tucker Condition 10

K-T Condition - Example 11

K-T Condition - Example 12

K-T Condition - Example l The above problem is reduced to : 13

K-T Theory l l l Theorem 1: (Necessity) Consider the NLP problem (1). Let f, g and h be differentiable and x* is the solution, also gj(x*) and hk(x*) be differentiable. Then there exist u*, v* solve K-T problem. Theorem 2 : (Sufficiency) Consider the NLP problem (1). Let f(x) be convex, g (x) be concave functions, and h(x) be linear if there exist x*, u* and v* solve K-T problem. , then x* is the optimality of (1). 14

K-T Theory - Example l f(x)=x 12 -x 2 (1, 1), (2, 2), (1. 5, 1. 5) f(1, 1)=0, f(2, 2)=2, f(1. 5, 1. 5)=0. 75<1 ∴f convex h 1=x 1+x 2 -6 linear g 1=x 1 -1 concave g 2=30 -x 12 -x 22 (1, 1), (2, 2), (1. 5, 1. 5) g 2(1, 1)=28, g 2(2, 2)=22, g 2(1. 5, 1. 5)=25. 5>25, ∴g 2 concave l The solution is global optimum l l l l 15

5 -5 Duality of Linear Programming l Primal problem: l The corresponding Lagrangian can be expressed by 16

Duality of Linear Programming l At x* l Also l Substitute for ci above get: 17

Duality of Linear Programming l The Dual Problem hence becomes: 18

Example – Primal Problem 19

Example – Dual Problem 20

Example: Charity Work l The local college’s School of American Craftsman has decided to participate seriously in a local charity event by manufacturing special commemorative desks, tables, and chairs. Resources are restricted as shown in the next table. The local lumber cooperative has donated 48 board feet of lumber. Faculty and staff have volunteered 20 finishing hours and 8 carpentry hours. The desk will be sold for $60, the table $30 and the chair for $20. The school does not expect to sell more than 5 tables. How does the school should do to maximize the profit? 21

Example: Charity Work. Continued Resources Desk Table Chair Lumber (Board feet) 8 6 1 Finishing hours (hours) 4 2 1. 5 Carpentry (hours) 2 1. 5 0. 5 22

Example: Charity Work. Continued (Primal and Dual) l Primal: l Dual: 23

Example: Charity Work. Continued (MATLAB Code) %Primal b=[48; 20; 8; 5]; Aeq=[]; beq=[]; UB=[Inf Inf]'; LB=[0 0 0]'; f=[-60; -30; -20]; A=[8 6 1; 4 2 1. 5; 2 1. 5 0. 5; 0 1 0]; [X, FVAL, EXITFLAG, OUTPUT, LAMBDA]=LINPROG(f, A, b, Aeq, beq, LB, UB); X' LAMBDA. ineqlin %Dual ff=f; AA=-A'; bb=b; UB=[Inf Inf Inf]'; LB=[0 0 0 0]'; [X, FVAL, EXITFLAG, OUTPUT, LAMBDA]=LINPROG(bb, AA, ff, Aeq, beq, LB, UB) X' LAMBDA. ineqlin 24

Example: Charity Work. Continued (MATLAB Result) l >> Optimization terminated successfully. ans = 2. 0000 0. 0000 8. 0000 ans = 0. 0000 10. 0000 Optimization terminated successfully. ans = 0. 0000 10. 0000 ans = 2. 0000 0. 0000 8. 0000 25

5 -6 MATLAB NLP tool l l FMINCON Finds a constrained minimum of a function of several variables. FMINCON solves problems of the form: min F(X) subject to: A*X <= B, Aeq*X = Beq (linear constraints) X C(X) <= 0, Ceq(X) = 0 (nonlinear constraints) LB <= X <= UB l l l X=FMINCON(FUN, X 0, A, B) starts at X 0 and finds a minimum X to the function FUN, subject to the linear inequalities A*X <= B. FUN accepts input X and returns a scalar function value F evaluated at X. X 0 may be a scalar, vector, or matrix. 26

MATLAB NLP tool-continued l l X=FMINCON(FUN, X 0, A, B, Aeq, Beq) minimizes FUN subject to the linear equalities Aeq*X = Beq as well as A*X <= B. (Set A=[] and B=[] if no inequalities exist. ) l l l X=FMINCON(FUN, X 0, A, B, Aeq, Beq, LB, UB) defines a set of lower and upper bounds on the design variables, X, so that a solution is found in the range LB <= X <= UB. Use empty matrices for LB and UB if no bounds exist. Set LB(i) = -Inf if X(i) is unbounded below; set UB(i) = Inf if X(i) is unbounded above. 27

MATLAB NLP tool-continued l l l X=FMINCON(FUN, X 0, A, B, Aeq, Beq, LB, UB, NO NLCON) subjects the minimization to the constraints defined in NONLCON. The function NONLCON accepts X and returns the vectors C and Ceq, representing the nonlinear inequalities and equalities respectively. FMINCON minimizes FUN such that C(X)<=0 and Ceq(X)=0. (Set LB=[] and/or UB=[] if no bounds exist. ) 28

Example: Multi-Stage compressor (MATLAB Code) A=[-1 0; 1 -1; 0 1]; B=[-1; 0; 64]; X 0=[2; 10]; X=FMINCON('stage_com', X 0, A, B) function obj=stage_com(x); x 1=x(1); x 2=x(2); obj=x 1^(0. 25)+(x 2/x 1)^0. 25+(64/x 2)^(0. 25); 29

Example: Multi-Stage compressor (MATLAB Result) >> Warning: Large-scale (trust region) method does not currently solve this type of problem, switching to medium-scale (line search). > In C: MATLAB 6 p 5toolboxoptimfmincon. m at line 213 In C: MATLAB 6 p 5workstage_com_main. m at line 4 Optimization terminated successfully: Magnitude of directional derivative in search direction less than 2*options. Tol. Fun and maximum constraint violation is less than options. Tol. Con No Active Constraints X= 3. 9994 16. 0011 30

Example 31

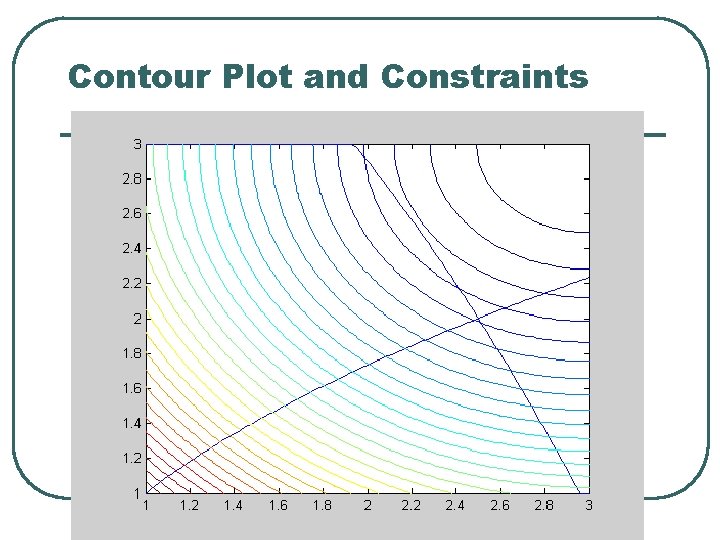
Contour Plot and Constraints 32

MATLAB PROGRAM X 0=[2 1]; A=[]; B=[]; Aeq=[]; Beq=[]; LB=[0 0]; UB=[5 5]; l X=FMINCON('examp_FUN', X 0, A, B, Aeq, Beq, LB, UB, 'exa mp_NONLCON') l function y=examp_FUN(x) l y=(x(1)-3)^2+(x(2)-3)^2; l function [c, ceq]=examp_NONLCON(x) l ceq=[]; l c(1)=-2*x(1)+x(2)^2+1; l c(2)=0. 8*x(1)^2+2*x(2)-9; l X= 2. 5000 2. 0000 l 33