Chapter 5 Multiplication of fractions decimals and negative


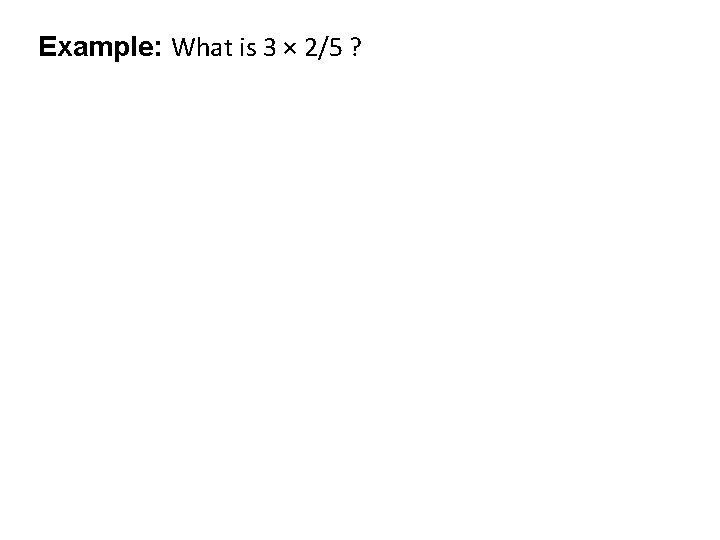
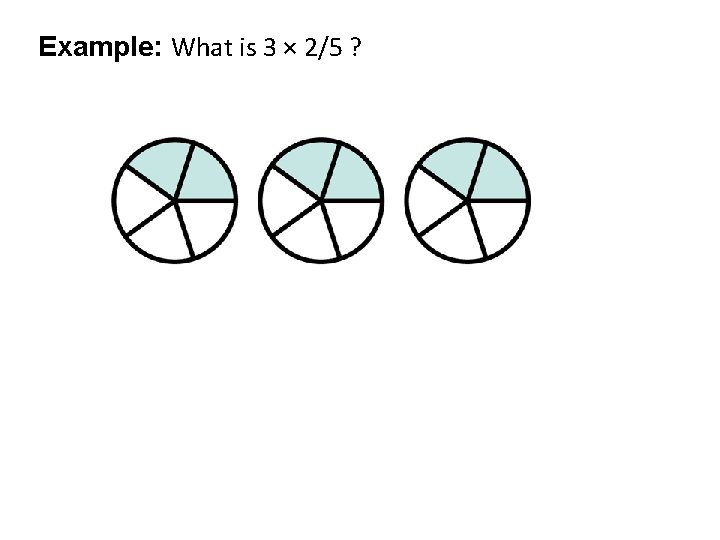
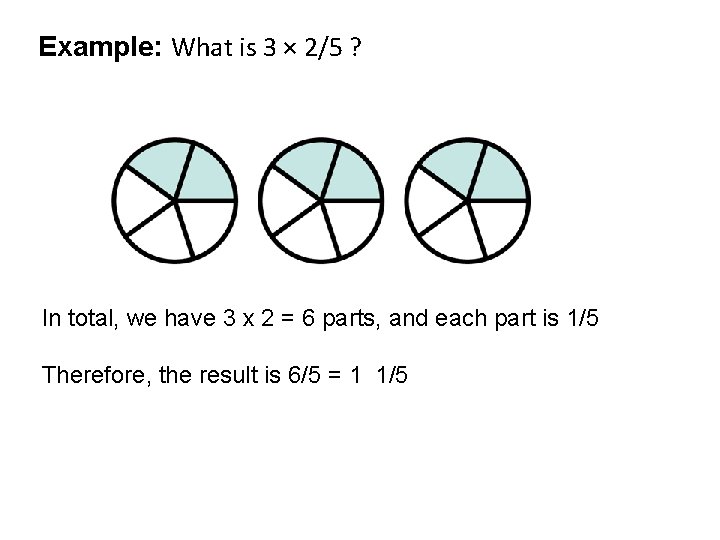






















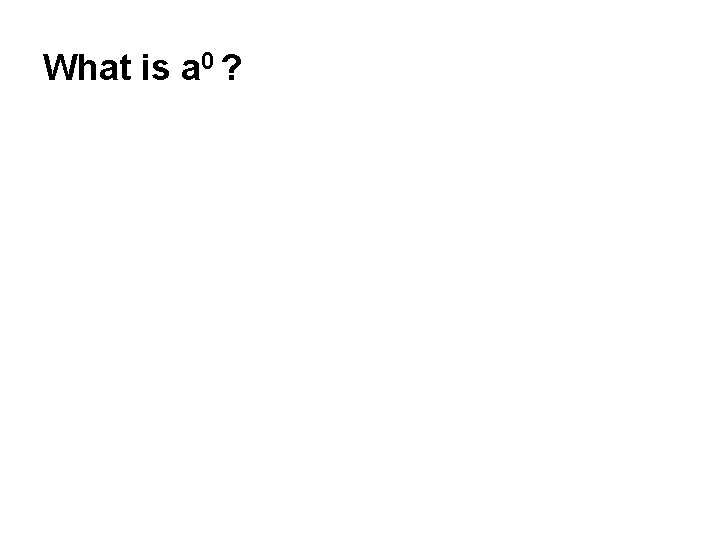


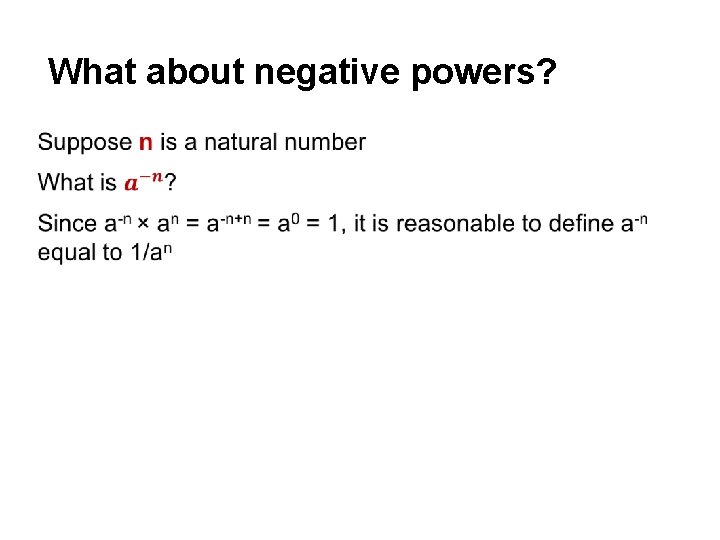






- Slides: 44

Chapter 5. Multiplication of fractions, decimals, and negative numbers

Multiplying Fractions Recall: If A and B are nonnegative numbers, then A × B is the product of A and B, in which A means the number of groups, B means the number of objects in each group and A × B means the total number of objects in A groups of B. The same idea applies if we consider fractions and decimals.
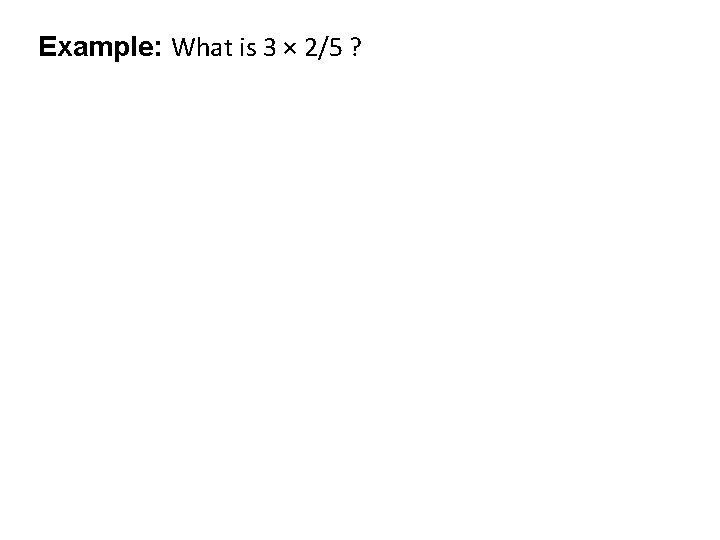
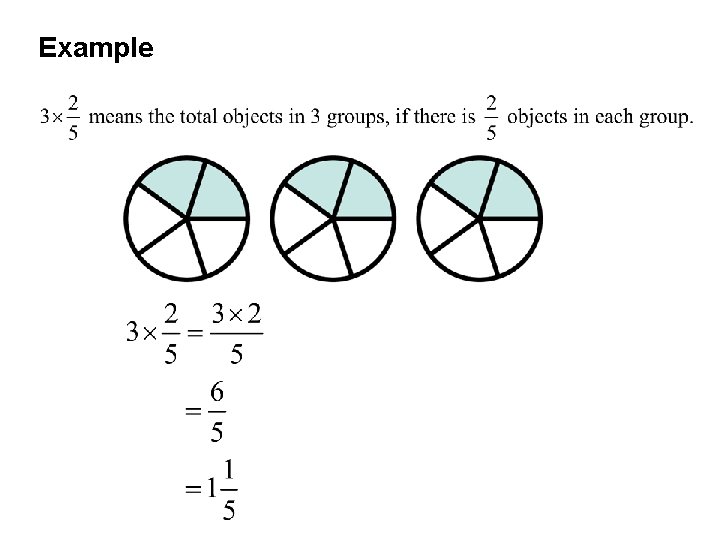
Example: What is 3 × 2/5 ?
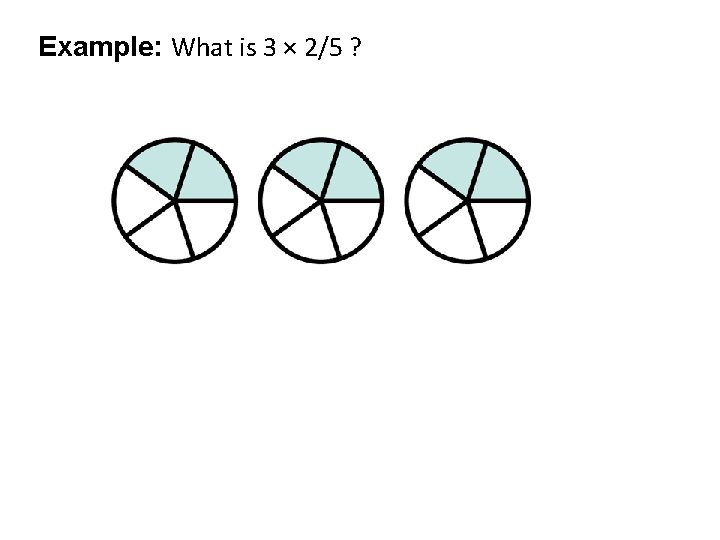
Example: What is 3 × 2/5 ?
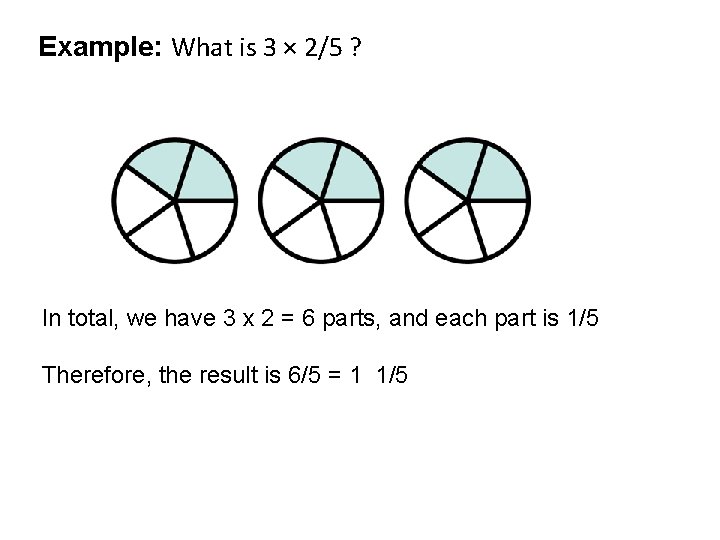
Example: What is 3 × 2/5 ? In total, we have 3 x 2 = 6 parts, and each part is 1/5 Therefore, the result is 6/5 = 1 1/5

Example

What if we need to multiply two fractions?




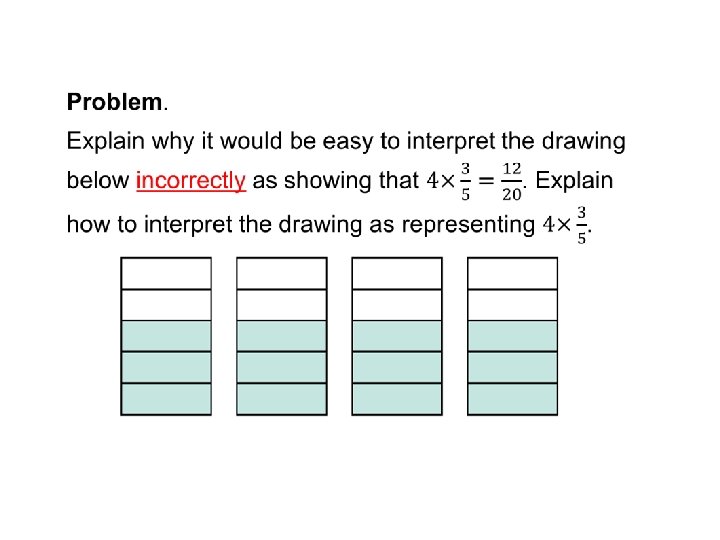
Problem. Briefly discuss the difference between parts (a) and (b).

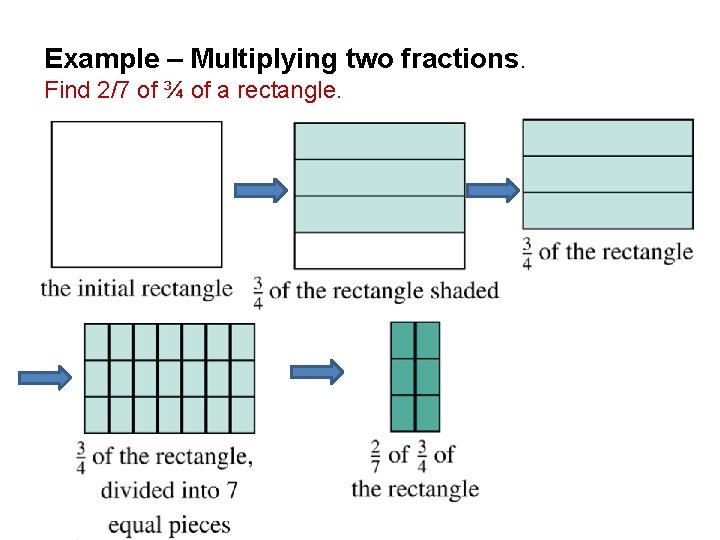
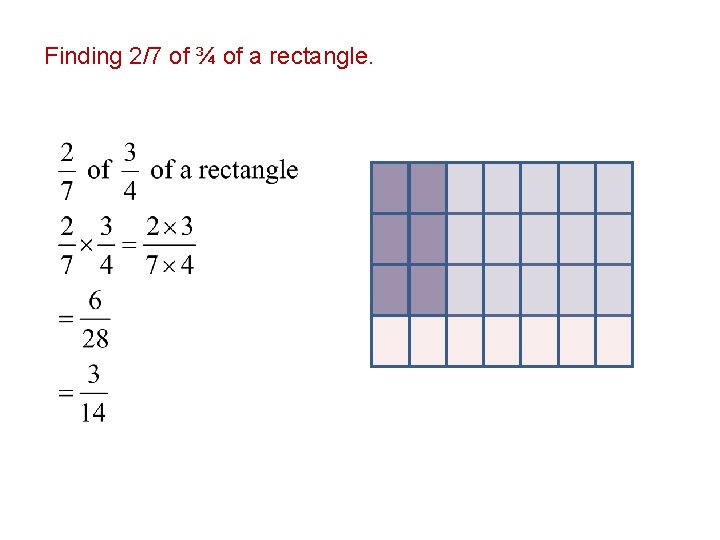
Example – Multiplying two fractions. Find 2/7 of ¾ of a rectangle.

Finding 2/7 of ¾ of a rectangle.


Fraction Multiplication In General When multiplying two fractions we multiply the numerators and multiply the denominators. Consequently, we have:



Multiplying Decimals Step 1: Multiply the two numbers without the decimal point according to the multiplication algorithm. Step 2: Add the number of digits to the right of the decimal point of both numbers. Step 3: In the answer you have found in step 1, count the number of digits you found in step 2 from right to left and put the decimal point in the respective position.

Example: Multiply 0. 48 by 3. 9. Step 1: Multiply the two numbers without the decimal points: Step 2: Add the decimal of both numbers: There are 3 decimals in total. Step 3: For the final answer, count in the number you found by multiplying the two numbers the three decimals from the right and place your decimal point. The final answer will be 1. 872 since we had 3 decimals counted for.

Why does this algorithm for multiplication of the decimals make sense? Let us go back to 3. 9 x 0. 48=1. 872

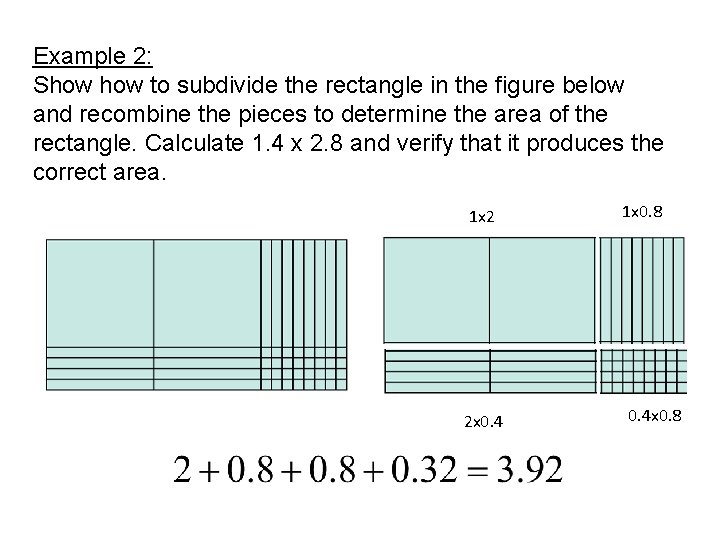
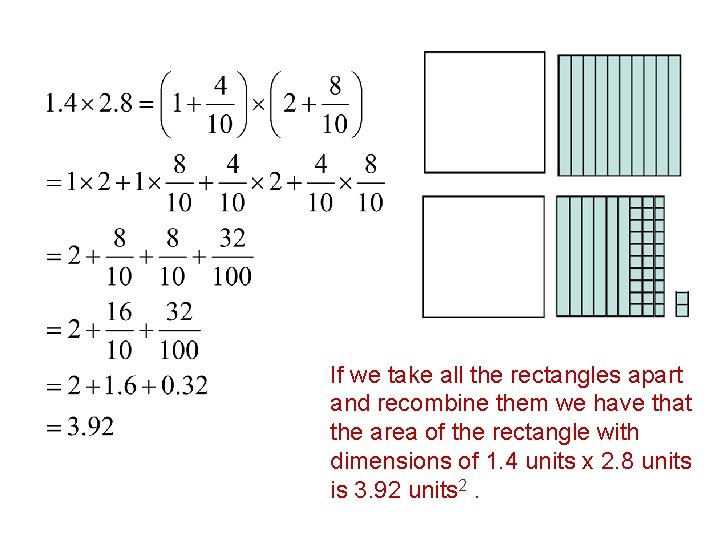
Example 2: Show to subdivide the rectangle in the figure below and recombine the pieces to determine the area of the rectangle. Calculate 1. 4 x 2. 8 and verify that it produces the correct area. 1 x 2 2 x 0. 4 1 x 0. 8 0. 4 x 0. 8

If we take all the rectangles apart and recombine them we have that the area of the rectangle with dimensions of 1. 4 units x 2. 8 units is 3. 92 units 2.


Multiplying Negative Numbers What should 3 × (-2) mean? • Using the original definition of multiplication: 3 groups of -2 objects in each group (e. g. you owe 2 dollars to each of 3 people) • Thus we have 6 owing objects, or -6 What should -2 × 3 mean? • -2 could be the number of owing groups, with 3 objects in each (e. g. you give away three dollars twice) • Therefore the result is still -6

Alternatively, we can use addition to define multiplication: 3 × (-2) = (-2) + (-2) = -6 Assuming that commutative property should still hold, we get: -2 × 3 = 3 × (-2) = -6

Multiplying Negative Numbers – General Rules For multiplication of negative numbers, all the multiplicative properties, such as commutative property, associative property, and the distributive property of multiplication over addition are still valid: - A × B = B × (- A) (-A × B) × C = - A × (B × C) - A × (B + C) = - A × B + (- A × C)

What about the product of two negative numbers?

How do we multiply two negative numbers? We shall use the distributive property of multiplication over addition: In General:

Exercise. Find a practical way to interpret multiplication of two negative numbers


Powers and Scientific Notation

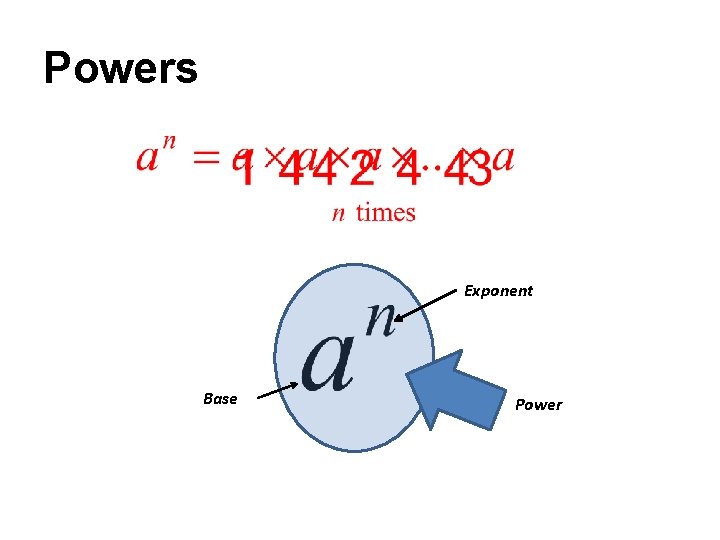
Powers Exponent Base Power

Exercise. Compute 2 n for all n from 1 to 10.

Main property of powers m a × n a = m+n a
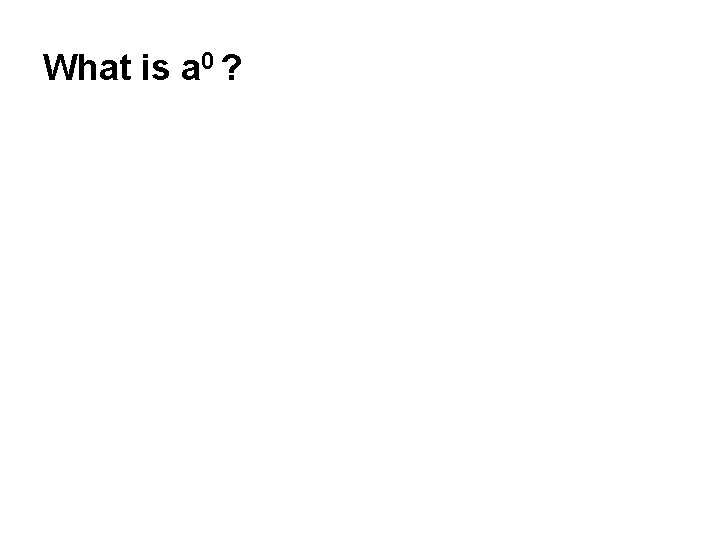
What is a 0 ?

What is a 0 ? • Note that am×an = am+n • Therefore am×a 0 = am+0 =am

What is a 0 ? • Note that am×an = am+n • Therefore am×a 0 = am+0 =am • Thus it is reasonable to define a 0 = 1 for all non-zero a • 00 is undefined
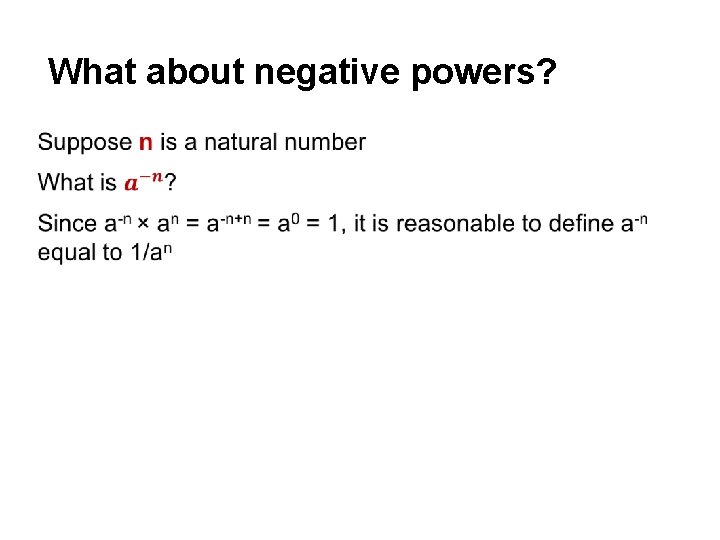
What about negative powers?

Negative powers

Powers of 10:

Scientific Notation A number is in scientific notation, if it is written as decimal that has exactly one nonzero digit to the left of the decimal point, multiplied by a power of 10


Problem. Suppose you multiply a 6 digit number by 8 digit number. How many digits will the product have?
