Chapter 5 Methods An overview In Add 2

Chapter 5 Methods

An overview In Add 2 Integers: println(“This program adds two integers. ”); int n 1 = read. Int(“Enter n 1: “); • • • method name: println argument (string): “This program adds two integers. ” operation: prints the argument (string) on the console return: no return value (void) When the call to println is completed, the program continues to the next statement

println(“This program adds two integers. ”); int n 1 = read. Int(“Enter n 1: “); • method name: read. Int • argument (string): “Enter n 1: “ • operation: prints the argument (string) on the console, then read an integer from the user (keyboard) • return: the integer entered by the user • This method can be viewed as an expression. It returns a value (integer). When the call to read. Int is completed, the program continues to store the value (integer) to variable n 1.

Beauty of methods • You don’t need to understand how read. Int is implemented. Just use it as a magic box. • You will use read. Int very often. • Most of you probably will never have to understand how read. Int is implemented. Information hiding

Methods vs programs • Input/output from/to the user should be part of a program, a service to a user. • A program passes/gets arguments/results to/from a method, a service to a programmer. • New programmers have a tendency to use input/output operations within methods when the logic of the situation calls for using arguments and results.

Method calls as expressions Method calls that return a value can be used as terms in an expression just like variables and constants. Example read. Int(“n 1: “) + read. Int(“n 2 “)

Math methods Static methods from the Math class: Math. abs(x), Math. sin(x), Math. sqrt(x) Figure 5 -1, p. 137 double distance = Math. sqrt(x*x + y*y); Note • you must include the class name Math when calling a Math method. • use x*x instead of Math. pow(x, 2)

Method calls as messages The Math methods are static methods, they belong to the class Math. In object-oriented languages like Java, the act of calling a method is often described in terms of sending a message. Objects communicate by sending messages. One object (the sender) invokes a method that belongs to another object (the receiver).

Method calls as messages (cont. ) One object (the sender) invokes a method that belongs to another object (the receiver). Example: rect. set. Color(Color. RED) sender: the current (calling) object receiver: rect object (an object of GRect) Pattern: receiver. method. Name(arguments)

If the receiver (target object) is this (current, calling object), the receiver can be omitted. println(value) is the same as this. println(value) Since the method println() is defined as a part of the Program class. Every subclass of Program inherits this method.

Writing your own methods visibility type name(parameters) { method body } • visibility: private or public, keep a method private if possible. • type: data type of the return value or void if no return value. • name: use a meaningful name Example private double celsius. To. Fahrenheit(double c) { implementation }

Returning a value from a method Pattern return expression Example private double feet. To. Inches(double feet) { return 12*feet; }

Example: temperature conversion /* * File: Temperature. Conversion. Table. java * --------------------------* This program creates a table of Celsius to Fahrenheit * equivalents. Lower and high limits and step are defined * as constants */ Import acm. program. *;

Public class Temperature. Conversion. Table extends Console. Program { public void run() { println(“Celsius to Fahrenheit table. ”); for (int c = LOWER_LIMIT; c <= UPPER_LIMIT; c += STEP_SIZE) { int f = (int) celsiu. To. Fahrenheit(c); println(c + “C = “ f + “F”); } } /* Returns the Fahrenheit equivalent of the Celsius temperature c. */ private double celsius. To. Fahrenheit(double c) { return (9. 0 / 5. 0) * c + 32. 0; /* Private constants */ private static final int LOWER_LIMIT = 0; private static final int UPPER_LIMIT = 100; Private static final int STEP_SIZE = 5; }

Example (cont. ) Note • method celsius. To. Fahrenheit belongs to this class, thus this (the receiver) can omitted. • Method println is defined as a part of Program, which is the superclass of this class, thus this (the receiver) can be omitted.

Methods involving control statements private int max(int m, int n) { if (m > n) { return m; } else { return n; } } same as return ((m > n)? m : n); return can be used at any points in a method and may appear more than once.

Nonnumerical methods private String weekday. Name(int day) { switch (day) { case 0: return "Sunday"; case 1: return "Monday"; case 2: return "Tuesday"; case 3: return "Wednesday"; case 4: return "Thursday"; case 5: return "Friday"; case 6: return "Saturday"; default: return "Illegal weekday"; } }

Methods returning graphical object /* A circle of radius r centered at (x, y) filled with color */ private GOval create. Filled. Circle(double x, double y, double r, Color color) { GOval circle = new GOval(x - r, y - r, 2 * r); circle. set. Filled(true); circle. set. Color(color); return circle; } Useful when drawing multiple filled circles.

Predicate methods Methods that return Boolean values. private boolean is. Divisible. By(int x, int y) { return x % y == 0; } Example for (int i = 1; i <= 100; i++) { if (is. Divisible. By(i, 7)) { println(i); } }

Testing power of 2 private boolean is. Power. Of. Two(int n) { if (n < 1) return false while (n > 1) { if (n % 2 == 1) return false; n /= 2; } return true; }

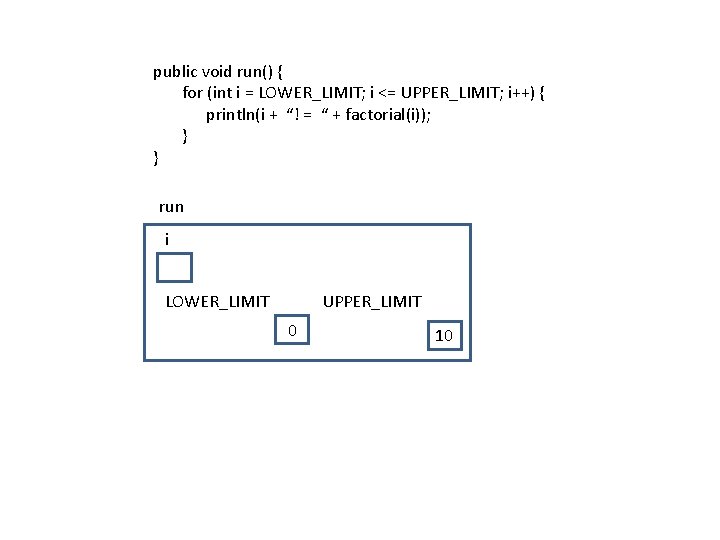
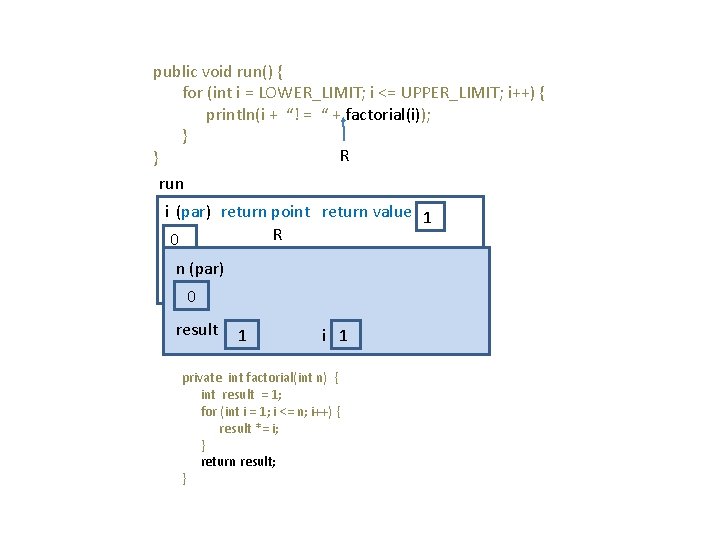
Method-calling mechanics Understand what happens during a method-call. Example main program public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } } Method private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; }

public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } } run i LOWER_LIMIT UPPER_LIMIT 0 10

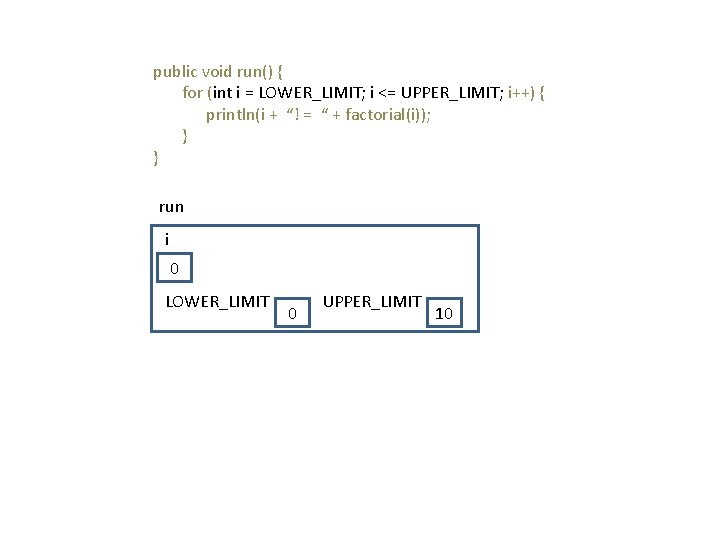
public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } } run i 0 LOWER_LIMIT 0 UPPER_LIMIT 10

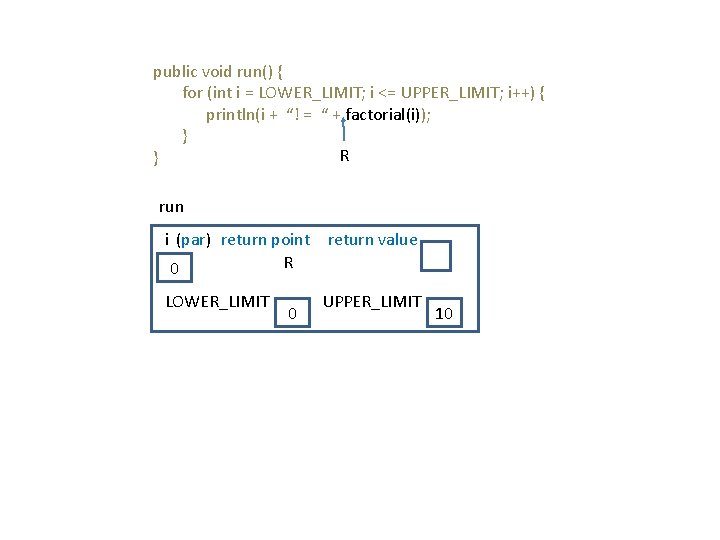
public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } R } run i (par) return point return value R 0 LOWER_LIMIT 0 UPPER_LIMIT 10

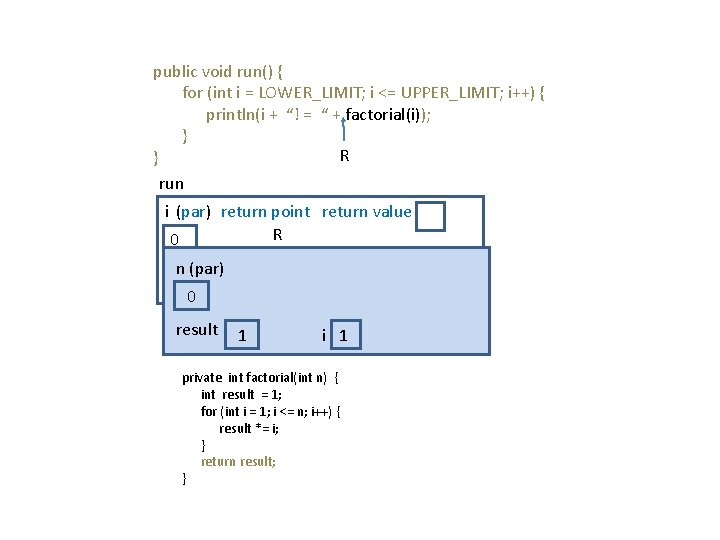
public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } R } run i (par) return point return value R 0 n (par) LOWER_LIMIT 0 0 result 1 UPPER_LIMIT 10 i 1 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; }

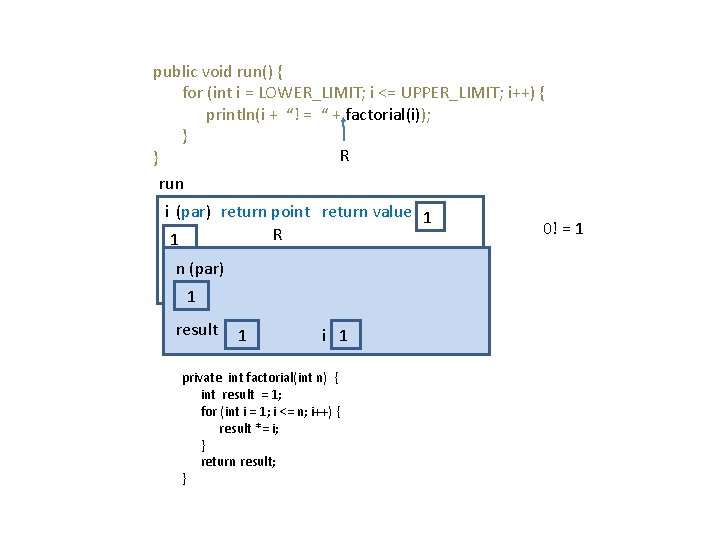
public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } R } run i (par) return point return value 1 R 0 n (par) LOWER_LIMIT 0 0 result 1 UPPER_LIMIT 10 i 1 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; }

public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } R } run i (par) return point return value 1 R 0 LOWER_LIMIT 0 UPPER_LIMIT 10 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; } 0! = 1

public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } } run i 0! = 1 1 LOWER_LIMIT 0 UPPER_LIMIT 10 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; }

public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } R } run i (par) return point return value 1 R 1 n (par) LOWER_LIMIT 0 1 result 1 UPPER_LIMIT 10 i 1 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; } 0! = 1

public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } R } run i (par) return point return value 1 R 1 LOWER_LIMIT 0 UPPER_LIMIT 10 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; } 0! = 1 1! = 1

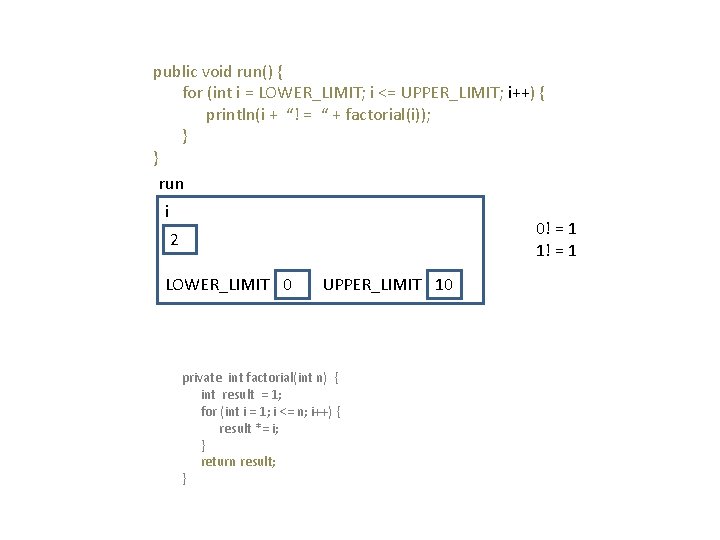
public void run() { for (int i = LOWER_LIMIT; i <= UPPER_LIMIT; i++) { println(i + “! = “ + factorial(i)); } } run i 0! = 1 1! = 1 2 LOWER_LIMIT 0 UPPER_LIMIT 10 private int factorial(int n) { int result = 1; for (int i = 1; i <= n; i++) { result *= i; } return result; }

Decomposition Decompose a large task into more manageable smaller tasks. Even further decompose some subtasks into still smaller subtasks. Decomposition strategy • Follow the structure if the real-world problem • Each subtask should perform a function that is easy to name and describe • Each level should take responsibility for certain details and avoid having those details percolate up to higher level

Example: Drawing a train Pseudocode public void run() { draw the engine draw the boxcar draw the caboose }

Arguments vs named constants In graphical problems, it is about the information needed to draw the right picture, such as sizes and locations. Two ways: • You can use named constants to define the parameters of the picture • You can pass this information as arguments to each method

Arguments vs named constants Using named constants is easy but inflexible, e. g. , the location of a boxcar may change Using arguments is more cumbersome but easy to change Guidelines • Use argument when caller will want to supply different values • Use named constants when caller will be satisfied with a single value

Draw. Train program Assumptions • The caller will always want to supply the location of each car. • All train cars are the same size and have the same basic structure. • Engines are always black. • Boxcars come in many colors, which means the caller must supply it. • Cabooses are always red.

Draw. Train program Headers • private void draw. Engine(double x, double y) • private void draw. Boxcar(double x, double y, Color color) • private void draw. Caboose(double x, double y)

Looking for common features Another useful strategy in choosing a decomposition is to look for features that are shared among several different parts of a program. Such common features can be implemented by a single method. Common structure in Draw. Train • the frame for the car, • the wheels on which it runs, • a connector to link it to its neighbor.

• The engine is black and adds a smokestack, cab, and cowcatcher. • The boxcar is colored as specified by the caller and adds doors. • The caboose is red and adds a cupola. You can use a single draw. Car. Frame method to draw the common parts of each car, as described in the text.

Algorithmic methods Greatest common divisor problem: int gcd(int x, int y) x, y: positive integers gcd(49, 35) = 7 gcd(6, 18) = 6 gcd(32, 33) = 1

A brute force approach public int gcd(int x, int y) { int guess = Math. min(x, y); while (((x % guess) != 0) || ((y % guess) != 0)) { guess--; } }

• Correctness: while loop terminates if !(((x % guess) != 0) || ((y % guess) != 0)) From De Morgan’s law, it is equivalent to ((x % guess) == 0) && ((y % guess) 0= 0) Thus the final guess is a common divisor. The program counts downward, the final guess is the first common divisor, so the greatest. • Termination: initial guess is a positive integer, then decremented in the program. Eventually, it will reach 1, which is always a common divisor. The loop terminates.

Euclid’s algorithm int gcd(int x, int y) { int r = x % y; while (r != 0) { x = y; y = r; r = x % y; } return y; }

• Correctness and termination: beyond the scope of this course. • Efficiency: gcd(1000005, 1000000) brute force: 2000000 – 8 % operations Euclid’s: 2 % operations gcd(1000000, 1000005) Euclid’s: 3 % operations