Chapter 5 Magnetostatics 5 1 The Lorentz Force


























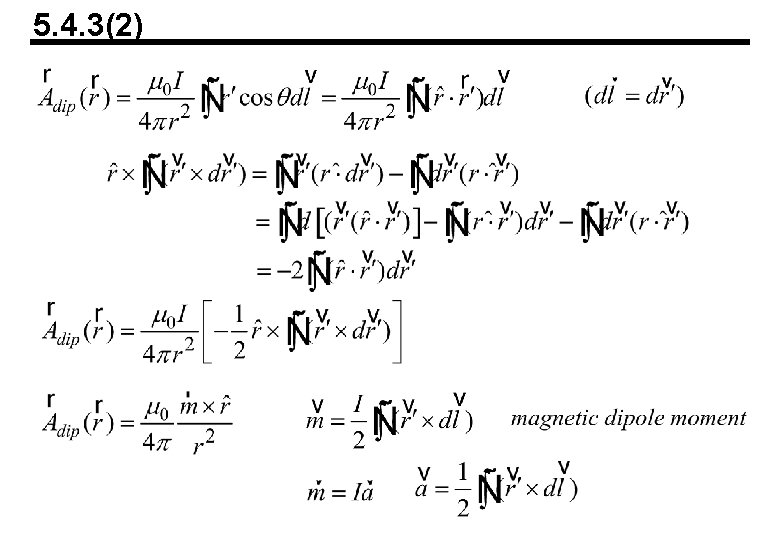
- Slides: 44

Chapter 5 Magnetostatics 5. 1 The Lorentz Force Law 5. 2 The Biot-Savart Law 5. 3 The Divergence and Curl of 5. 4 Magnetic Vector Potential

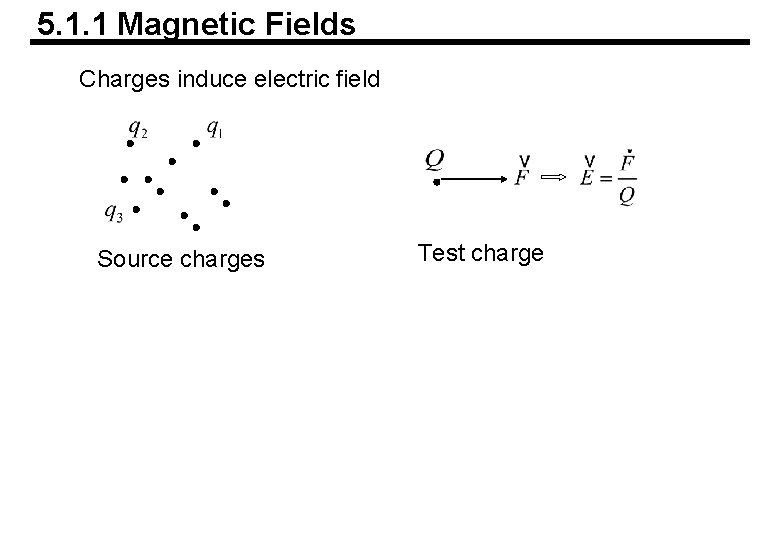
5. 1. 1 Magnetic Fields Charges induce electric field Source charges Test charge

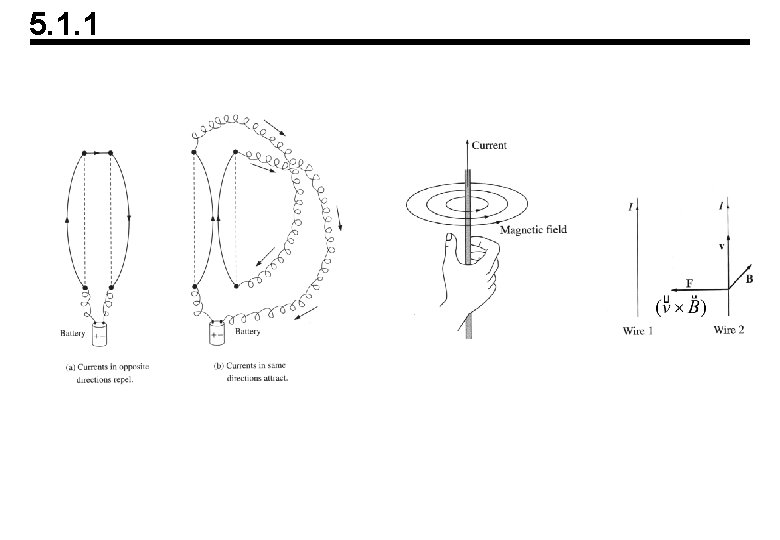
5. 1. 1

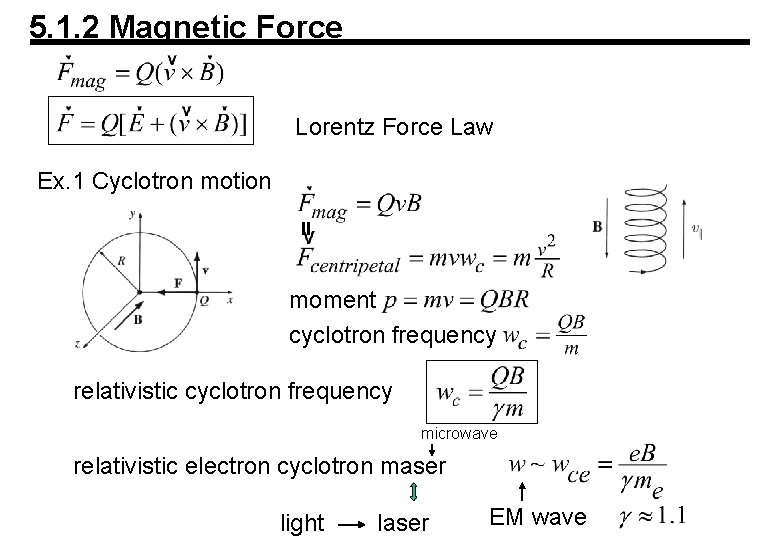
5. 1. 2 Magnetic Force Lorentz Force Law Ex. 1 Cyclotron motion moment cyclotron frequency relativistic cyclotron frequency microwave relativistic electron cyclotron maser light laser EM wave

5. 1. 2 (2) ~1960 EM : maser [ 1959 J. Schneider ; A. V. Gaponov] ES : space [1958 R. Q. Twiss ] (1976) K. R. Chu & J. L. Hirshfield : physics in gyrotron/plasma 1978 C. S. Wu & L. C. Lee : EM in space ( ) 1986 K. R. Chen & K. R. Chu : ES in gyrotron relativistic ion cyclotron instability 1993 K. R. Chen ES in Lab. plasma [fusion ( EM ? Lab. & space plasmas ? )]

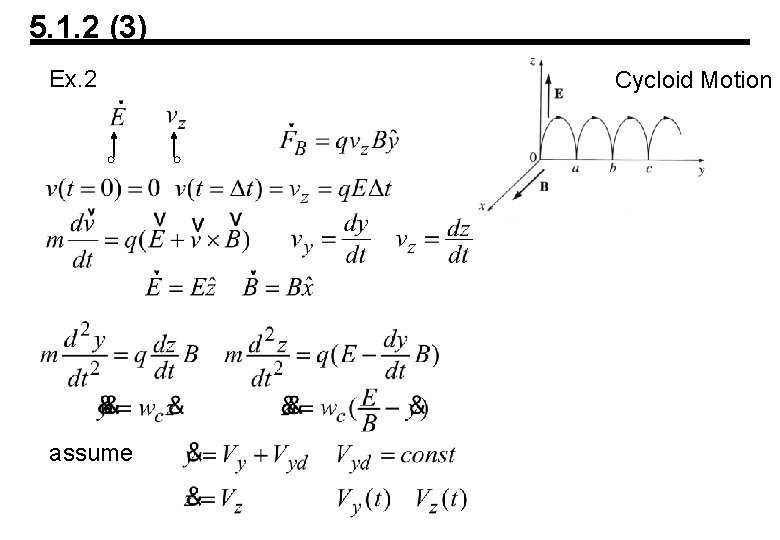
5. 1. 2 (3) Ex. 2 assume Cycloid Motion

5. 1. 2 (4)

5. 1. 2 (5)

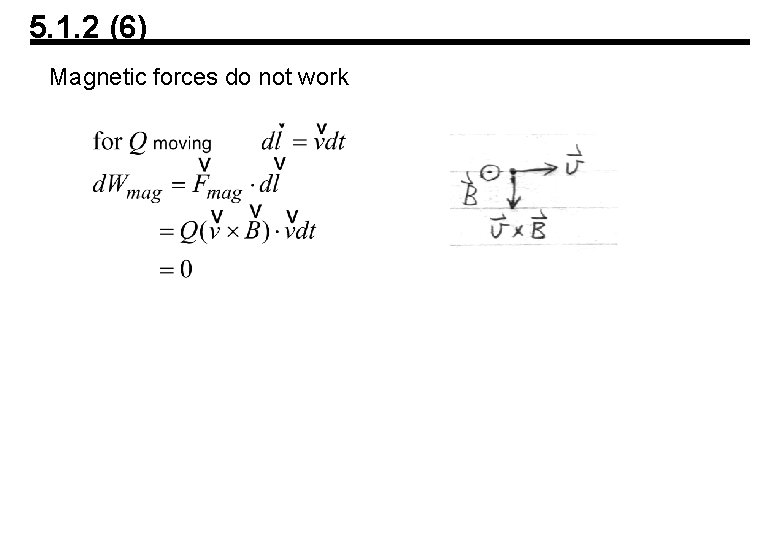
5. 1. 2 (6) Magnetic forces do not work

5. 1. 3 Currents The current in a wire is the charge per unit time passing a given point. Amperes 1 A = 1 C/S The magnetic force on a segment of current-carrying wire

5. 1. 3 (2) surface current density the current per unit length-perpendicular-to-flow (mobile) The magnetic force on a surface current is

5. 1. 3 (3) volume current density The current per unit area-perpendicular-to-flow The magnetic force on a volume current is

5. 1. 3 (4) Ex. 3 Sol. Ex. 4 Sol. (a) what is J ? (uniform I)

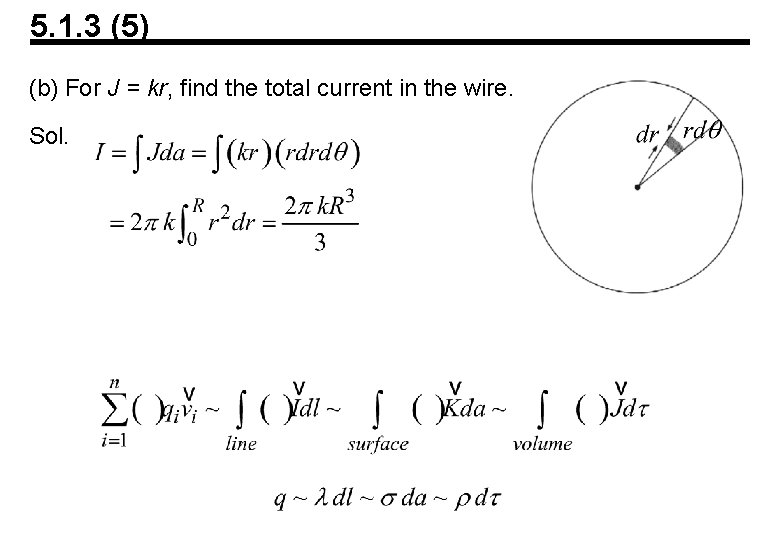
5. 1. 3 (5) (b) For J = kr, find the total current in the wire. Sol.

5. 1. 3 (6) relation? (charge conservation) Continuity equation

5. 2. 1 Steady Currents Stationary charges Steady currents constant electric field: electrostatics constant magnetic field: magnetostatics No time dependence

5. 2. 2 The Magnetic Field of a Steady Current Biot-Savart Law: for a steady line current Permeability of free space Biot-Savart Law for surface currents Biot-Savart Law for volume currents for a moving point charge

5. 2. 2 (2) Solution: In the case of an infinite wire,

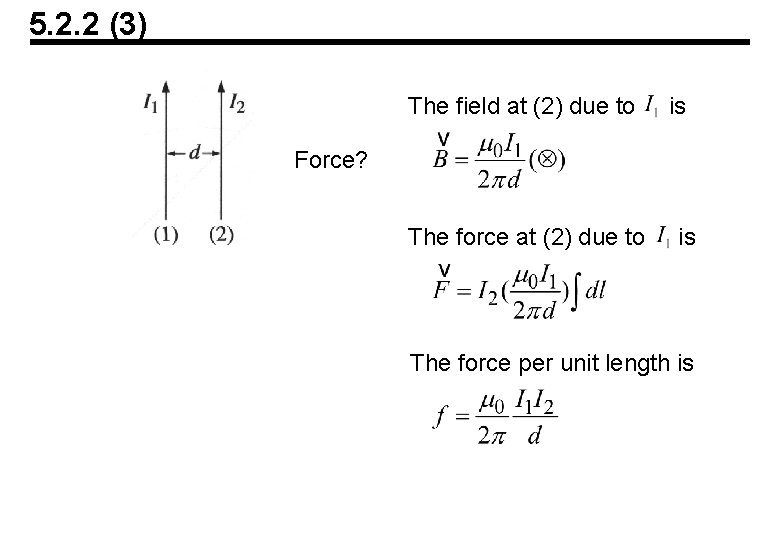
5. 2. 2 (3) The field at (2) due to is Force? The force at (2) due to is The force per unit length is

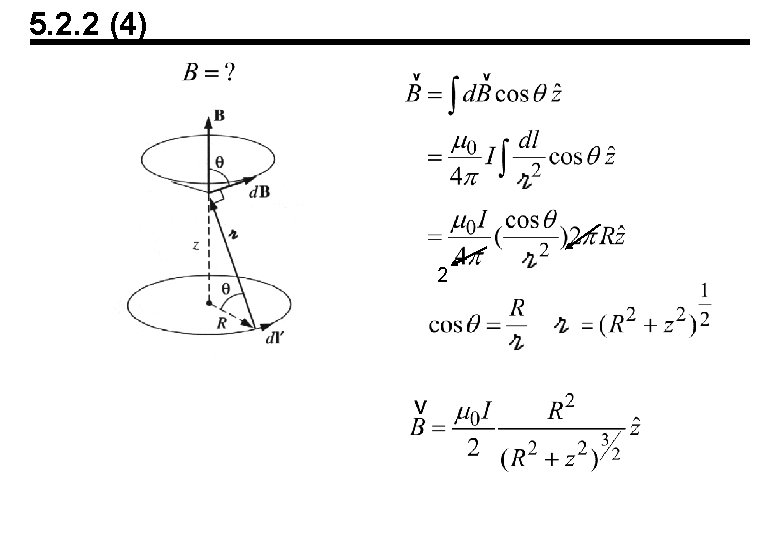
5. 2. 2 (4) 2

5. 3. 1 an example: Straight-Line Currents R

5. 3. 2 The Divergence and Curl of Biot-savart law

5. 3. 2 for steady current To where Ampere’s law in differential form

5. 3. 3 Applications of Ampere’s Law in differential form Ampere’s Law in integral form Electrostatics: Coulomb Gauss Magnetostatics: Bio-Savart Ampere The standard current configurations which can be handled by Ampere's law: 1. Infinite straight lines 2. Infinite planes 3. Infinite solenoids 4. Toroid

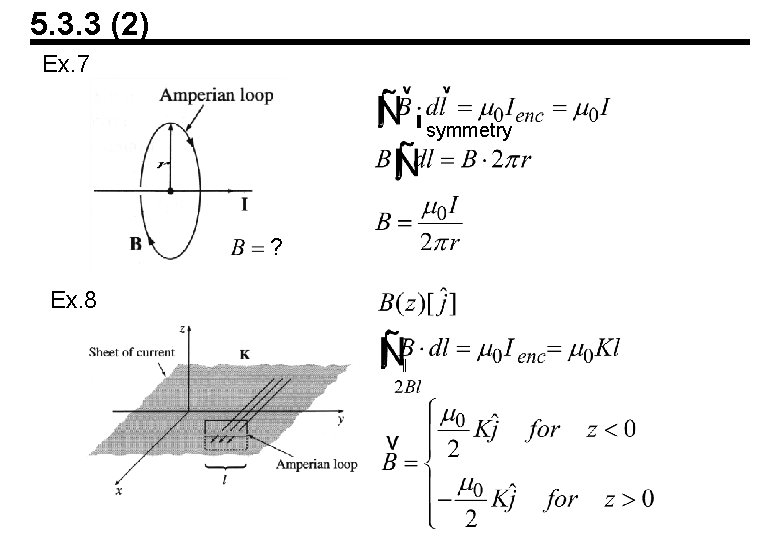
5. 3. 3 (2) Ex. 7 symmetry ? Ex. 8

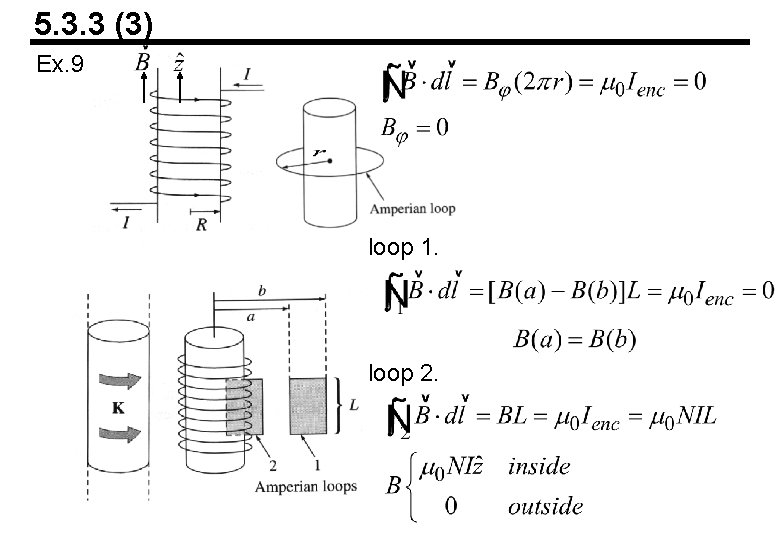
5. 3. 3 (3) Ex. 9 loop 1. loop 2.

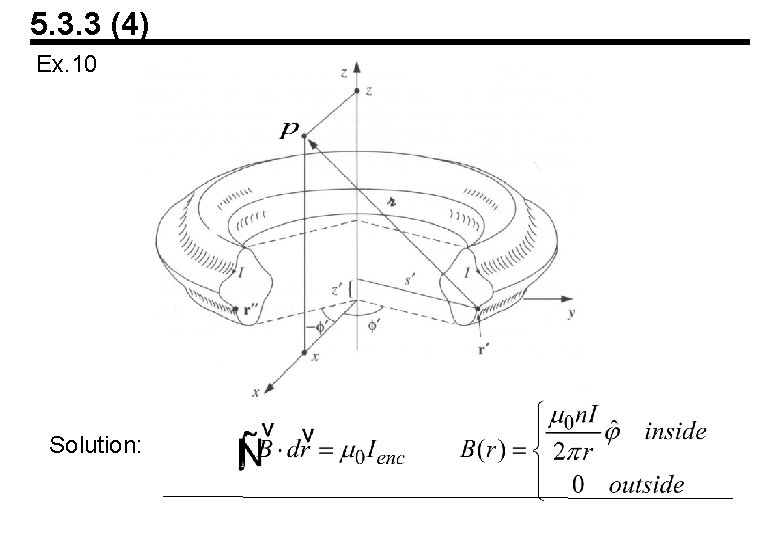
5. 3. 3 (4) Ex. 10 Solution:

5. 3. 3 (5)

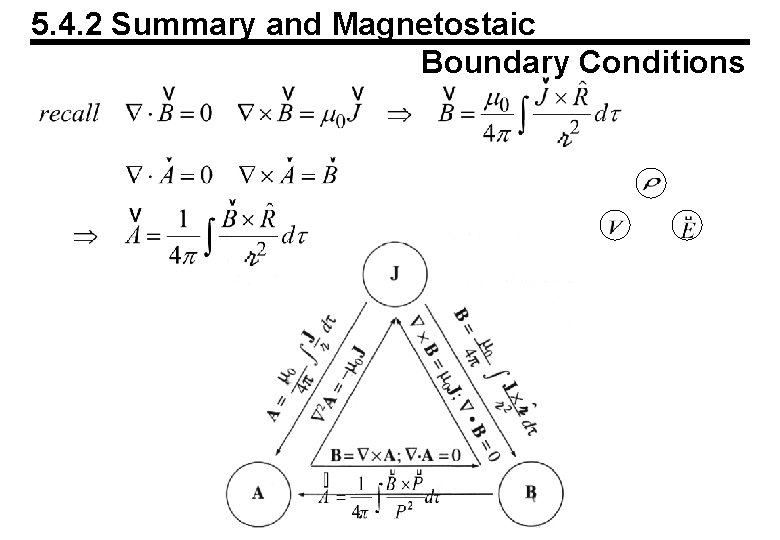
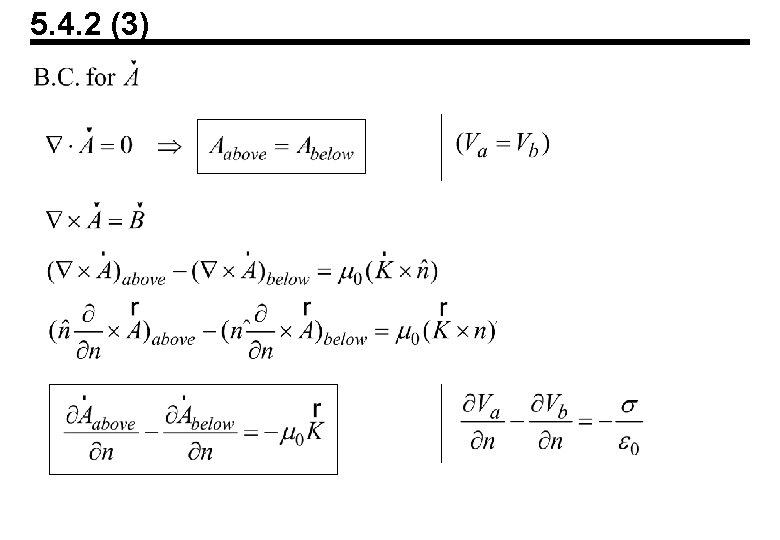
5. 4. 1 The Vector Potential E. S. : M. S. : a constant-like vector function Gauge transformation is a vector potential in magnetostatics If there is that with , can we find a function to obtain

5. 4. 1 (2) Ampere’s Law if

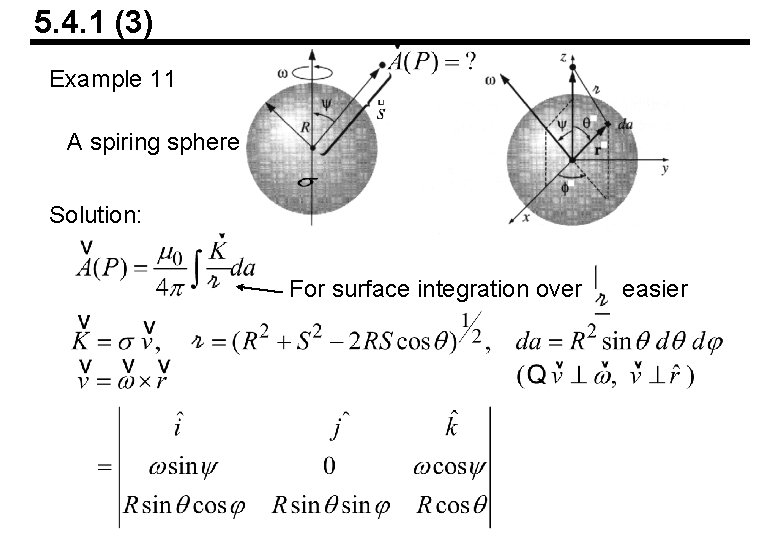
5. 4. 1 (3) Example 11 A spiring sphere Solution: For surface integration over easier

5. 4. 1 (4)

5. 4. 1 (5)

5. 4. 1 (6) if R > S if R < S

5. 4. 1 (7)

5. 4. 1 (8) Note: is uniform inside the spherical shell


5. 4. 2 Summary and Magnetostaic Boundary Conditions

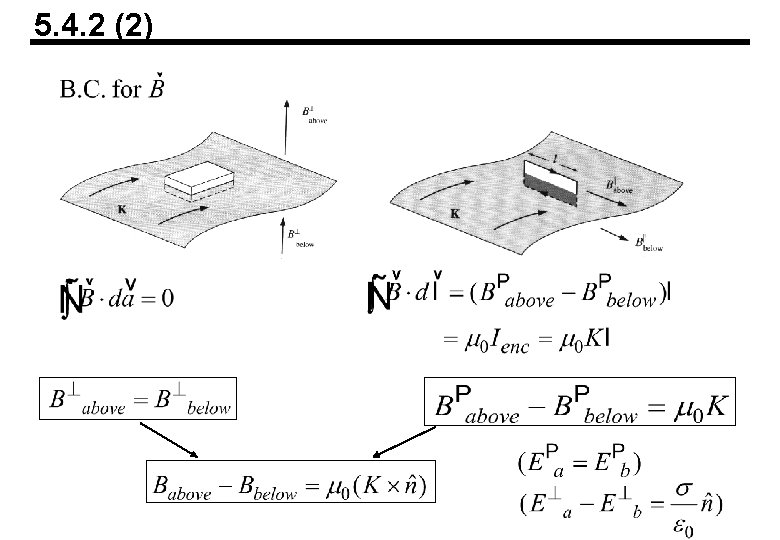
5. 4. 2 (2)

5. 4. 2 (3)

5. 4. 3 Multipole Expansion of the Vector Potential line current =0 monopole dipole
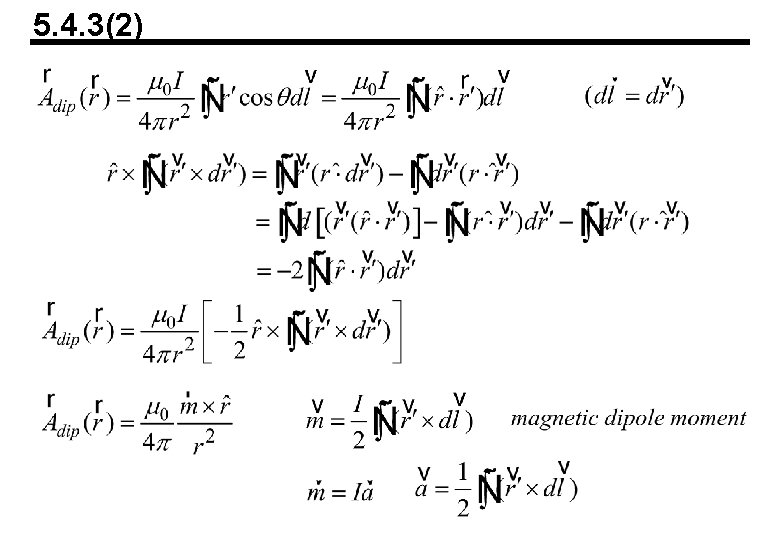
5. 4. 3(2)

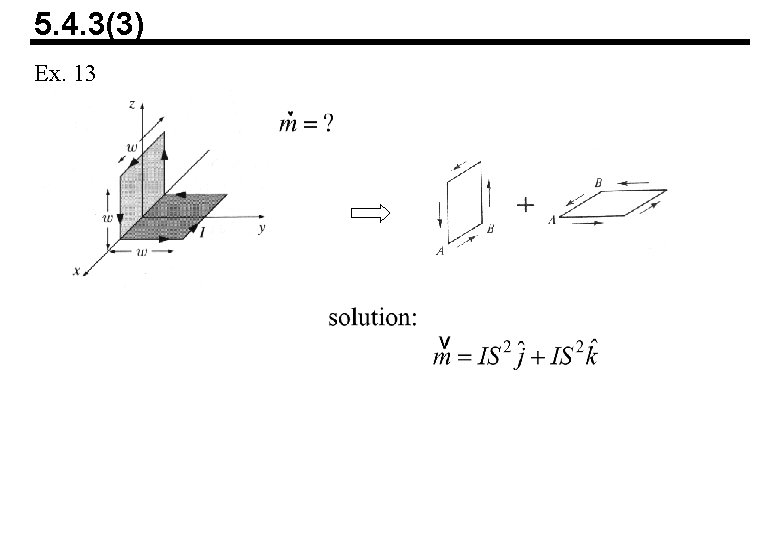
5. 4. 3(3) Ex. 13

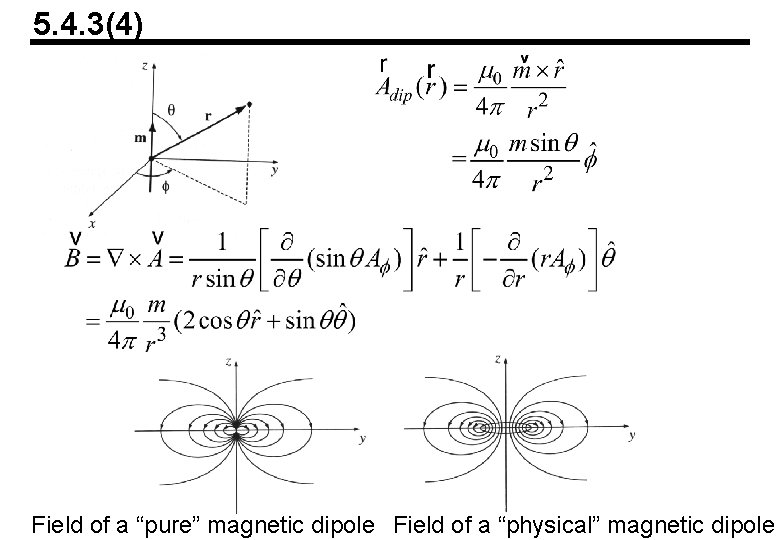
5. 4. 3(4) Field of a “pure” magnetic dipole Field of a “physical” magnetic dipole