Chapter 5 Machine Learning Learning 1 Rote learning

Chapter 5 Machine Learning

Learning 1. Rote learning rote(��� ) n. ������� , (by rote ������ ), ������ S. repetition 2. Learning by taking advice 3. Learning by problem solving Parameter adjustment Macro-Operators 4. Learning from examples Induction : Winston’s learning program p. 458 Version Spaces : Candidate eliminate algorithm Decision tree 5. Explanation-based learning p 482 323 -670 Artificial Intelligence 2 6. Formal learning theory Chapter 5

Winston’s learning program 323 -670 Artificial Intelligence 3 Chapter 5

Winston’s learning program Concept : P. 459 Begin with a structural description of one known instance of the concept. Call the description the concept definition. Examine descriptions of other known instances of the concepts. Generalize the definition to include them. Examine descriptions of near misses of concept, Restrict the definition to exclude these. 323 -670 Artificial Intelligence 4 Chapter 5

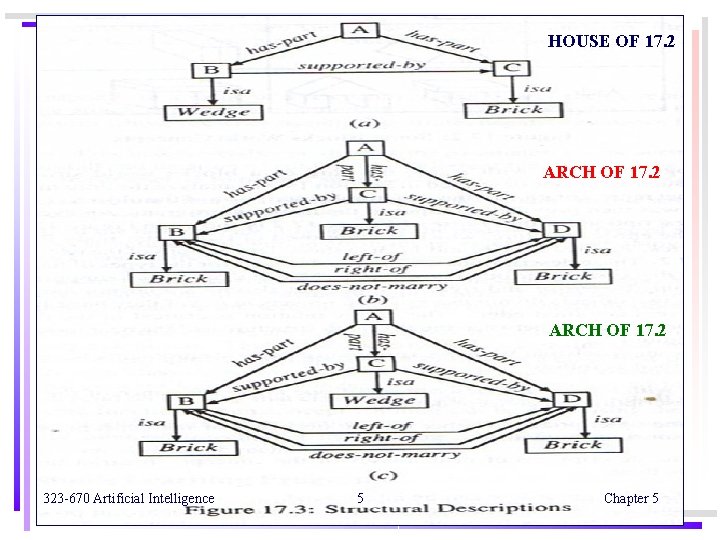
HOUSE OF 17. 2 ARCH OF 17. 2 323 -670 Artificial Intelligence 5 Chapter 5

Winston’s learning program 323 -670 Artificial Intelligence 6 Chapter 5

Winston’s learning program 323 -670 Artificial Intelligence 7 Chapter 5

Winston’s learning program 323 -670 Artificial Intelligence 8 Chapter 5

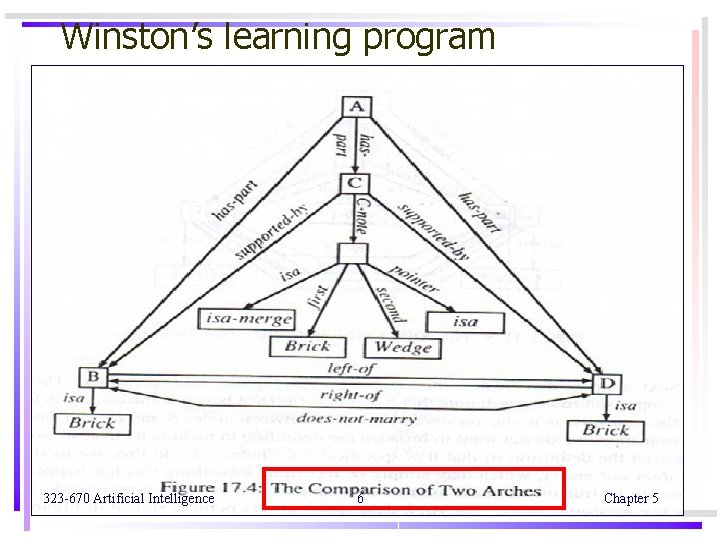
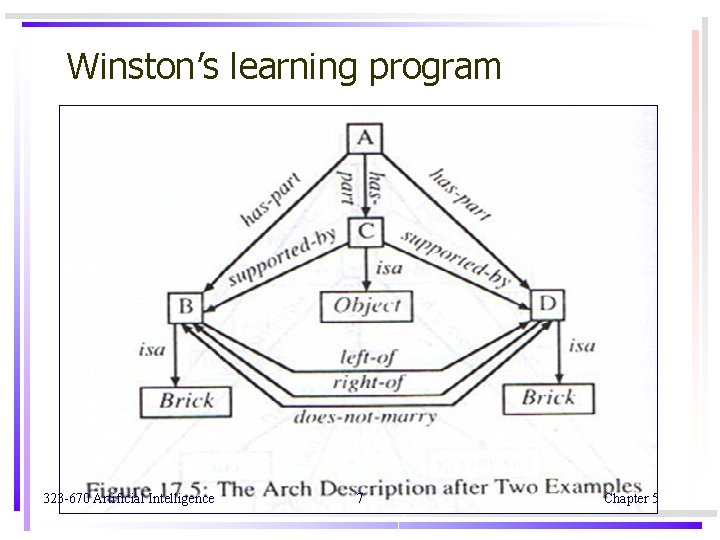
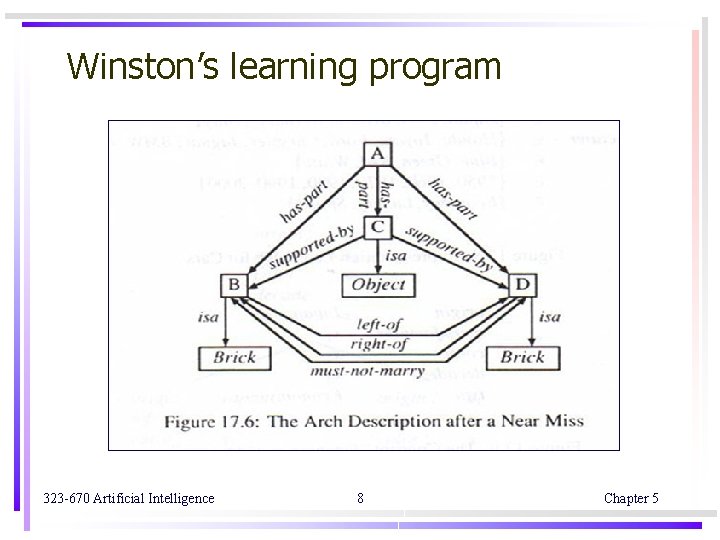
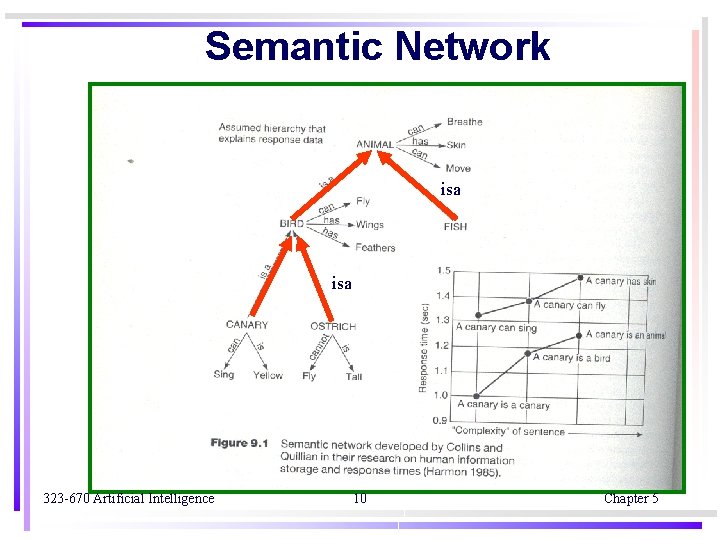
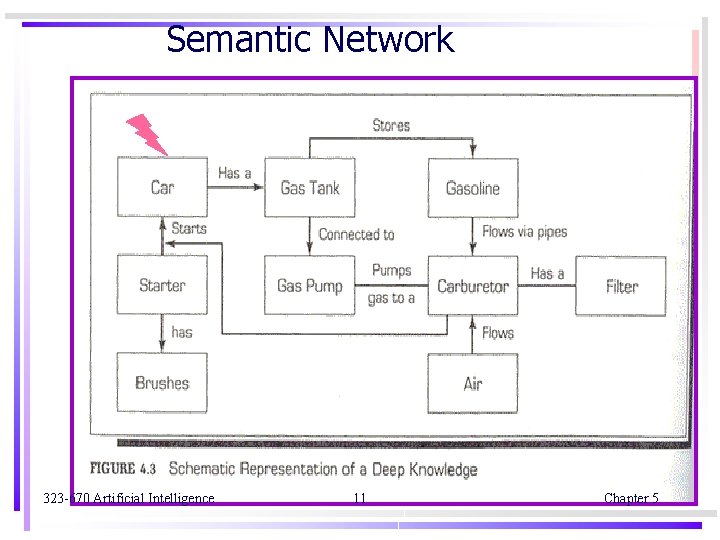
Winston’s learning program p. 458 Block world concept : Figure 17. 2 p. 459 Structure description : Figure 17. 3 p. 460 The comparison of two arches : Figure 17. 4 p. 461 The arch description after two examples : Figure 17. 5 p. 462 The arch “description after a near miss : Figure 17. 6 p. 463 use semantic networks to describe block structures use matching process to detect similarities and differences between structures use isa hierarchy to describe relationship among already known objects 323 -670 Artificial Intelligence 9 Chapter 5

Semantic Network isa 323 -670 Artificial Intelligence 10 Chapter 5

Semantic Network 323 -670 Artificial Intelligence 11 Chapter 5

Version Spaces The goal : to produce a description that is consistent with all positive examples but no negative examples in the training set. use frame representing concept for car see Figure 17. 7 p. 463 Features/Slots : { value 1, value 2, . . . , value. N } origin : { Japan, USA, Britain } Variables : X 1, X 2, X 3 concept space : see Figure 17. 11 Concept of Version Spaces p. 466 variables target concept all training instance 323 -670 Artificial Intelligence 12 Chapter 5

Version Spaces 323 -670 Artificial Intelligence 13 Chapter 5

Version Spaces • version space = current hypothesis = subset of concept space = largest collection of descriptions that is consistent with all the training examples seen so far. • concept space = G or S • G = contain the most general descriptions consistent with the training example seen so far. • S = contain the most specific descriptions consistent with training examples • positive example (+) move S to more specific • negative example (-) move G to more specific • if G and S sets converge the hypothesis is a single concept description 323 -670 Artificial Intelligence 14 Chapter 5

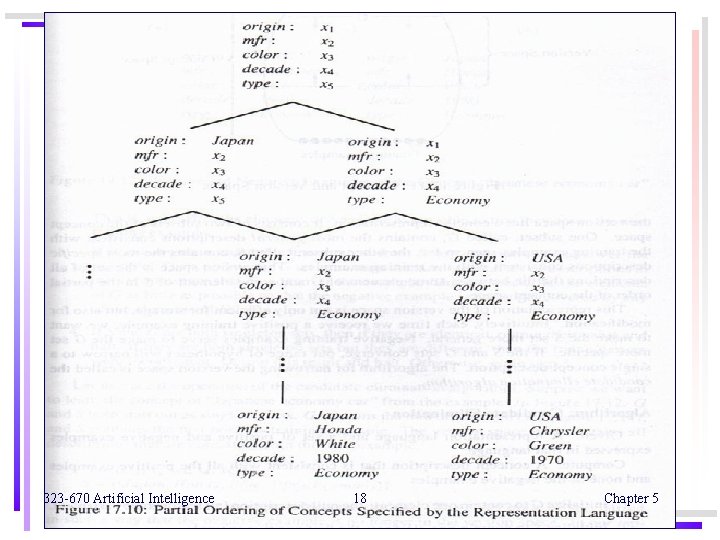
Version Spaces • Candidate Eliminate Algorithm p. 466 -467 • algorithm that use to narrow down the version space • by remove any descriptions that are inconsistent with set G and set S • Car Example Figure Figure 17. 7 Concept Car : p. 463 17. 8 Representation language for car : p. 464 17. 9 The concept Japanese car : p. 464 17. 10 Partial ordering of concepts : p. 465 17. 12 Positive and negative examples of car : p. 467 323 -670 Artificial Intelligence 15 Chapter 5

Version Spaces 323 -670 Artificial Intelligence 16 Chapter 5

Version Spaces 323 -670 Artificial Intelligence 17 Chapter 5

323 -670 Artificial Intelligence 18 Chapter 5

Version Spaces 323 -670 Artificial Intelligence 19 Chapter 5

Version Spaces 323 -670 Artificial Intelligence 20 Chapter 5

Candidate Eliminate Algorithm 323 -670 Artificial Intelligence 21 Chapter 5

Candidate Eliminate Algorithm 323 -670 Artificial Intelligence 22 Chapter 5

Version Spaces We want “Japanese economy car” From Figure 17. 12 Positive and negative examples of car : p. 467 [origin = X 1, manufacture = X 2, color = X 3, decade = X 4, type = X 5] GET EX 1 (+) G = {(X 1, X 2, X 3, X 4, X 5)} S = {(Japan, Honda, Blue, 1980, Economy}) =Figure 17. 12 in EX 1 GET EX 2 (-) G = {(X 1, Honda, X 3, X 4, X 5), (X 1, X 2, Blue, X 4, X 5) , (X 1, X 2, X 3, 1980, X 5), (X 1, X 2, X 3, X 4, Economy)} S = {(Japan, Honda, Blue, 1980, Economy}) ** the same because (-) example GET EX 3 (+) check G first, G = {(X 1, X 2, Blue, X 4, X 5) , (X 1, X 2, X 3, X 4, Economy)} S = {(Japan, X 2, Blue, X 4, Economy}) GET EX 4 (-) check G first, G = {(Japan, X 2, Blue, X 4, X 5) , (Japan, X 2, X 3, X 4, Economy)} S = {(Japan, X 2, Blue, X 4, Economy}) ** the same because (-) example GET EX 5 (+) check G first, G = {(Japan, X 2, X 3, X 4, Economy)} S = {(Japan, X 2, X 3, X 4, Economy}) 323 -670 Artificial Intelligence 23 Chapter 5

Version Spaces • Note : The algorithm is least commitment algorithm : produce as little as possible at each step • Problems 1. ) S and G may not converge to a single hypothesis 2. ) if there is a noise (inconsistent data) the algorithm will be premature, we may prune the target concept too fast * For example if the data number three given the negative sign () instance of positive sign (+). . . no matter how much the data is we can not find the concept. . * How to fix this problem is to maintain several G and S sets BUT it is costly and may have the bounded inconsistency problem 3. ) We can not use OR in the questions ask * For example : Italian sport car or German luxury car” 323 -670 Artificial Intelligence 24 Chapter 5

Decision Tree ID 3 Program = to classify a particular input, we start at the top of the tree and answer questions until we reach a leaf, where the classification is stored. See Figure 17. 13 Decision tree p. 470 1. Choose window = random subset of training examples to train 2. Outside window = use to test the decision tree 3. Use empirical evidence (iterative method) to build up decision tree 4. Building a node = choosing some attribute to divide training instance into subset consider (+) sign Can use with OR. . just change (-) sign into (+) sign Problems : noisy input, attribute value may be unknown, may have large decision tree and hard to understand relationship See Figure 17. 13 323 -670 Artificial Intelligence 25 Chapter 5

Decision Tree 323 -670 Artificial Intelligence 26 Chapter 5

Explanation-Based Learning • provide explanation • depend on domain theory/ domain knowledge 323 -670 Artificial Intelligence 27 Chapter 5

Formal Learning Theory • Given positive and negative examples • produce algorithm that will classify future examples correctly with probability 1/h • Complexity of learning : – the error tolerance (h) – the number of binary features present in the examples (t) – the size of the rule necessary to make the discrimination (f) 323 -670 Artificial Intelligence 28 Chapter 5

Formal Learning Theory • if the number of training examples required is polynomial in h, t, and f then the concept is learnable. • few training examples are needed learnable • we restrict the learner to the positive examples only. • See Figure 12. 22 Concept of elephant P. 483 • elephant = “gray, mammal, large” 323 -670 Artificial Intelligence 29 Chapter 5

Formal Learning Theory 323 -670 Artificial Intelligence 30 Chapter 5

Induction Øemphasis to all BEANS : all instances • induction : A method of reasoning by which one infers a generalization from a series of instances. • Inductive syllogisms are of the following form: 1. These beans are from this bag. (and these beans. . . , etc. ) 2. These beans are (all) white. # 3 Therefore, all beans from this bag are white. • In a much broader sense, induction can be thought to include various other forms of reasoning including reasoning, inference to cause form symptoms, and confirmation of laws and theories. Ø 1 323 -670 Artificial Intelligence Ø 2 31 Chapter 5

Deduction Øemphasis to one BEAN : one instance • deduction - A method of reasoning by which one infers a conclusion from a set of sentences by employing the axioms and rules of inference for a given logical system. • Use the term 'deduction' in a general sense to denote the fact that a conclusion follows necessarily from the premises. • Deductive syllogisms in quantificational predicate calculus are of the following form: Ø 1 1. All beans from this bag are white. . 2. These beans are from this bag. #4 Therefore, these beans are white. . . 323 -670 Artificial Intelligence 32 Ø 2 Chapter 5

Abduction Øemphasis to one BEANS • abduction -A method of reasoning by which one infers to the. . . best explanation. . . • - A heuristic procedure that reasons inductively from available empirical evidence to the discovery of the probable hypotheses that would best explain its occurrence. • Abductive syllogisms are of the following form: #3 All beans from this bag are white #4 These beans are white. 323 -670 Artificial Intelligence 33 Chapter 5

The End 323 -670 Artificial Intelligence 34 Chapter 5