Chapter 5 Joint Probability Distributions and Random Samples

5. 1 Jointly Distributed Random Variables Copyright (c) 2004 Brooks/Cole, a division of Thomson

Joint Probability Mass Function Let X and Y be two discrete rv’s defined on the sample space of an experiment. The joint probability mass function p(x, y) is defined for each pair of numbers (x, y) by Let A be the set consisting of pairs of (x, y) values, then Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Marginal Probability Mass Functions The marginal probability mass functions of X and Y, denoted

Joint Probability Density Function Let X and Y be continuous rv’s. Then f (x, y) is a joint probability density function for X and Y if for any two-dimensional set A If A is the two-dimensional rectangle Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

A = shaded rectangle = Volume under density surface above A Copyright (c) 2004

Marginal Probability Density Functions The marginal probability density functions of X and Y, denoted f. X(x) and f. Y(y), are given by Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Independent Random Variables Two random variables X and Y are said to be independent if for every pair of x and y values when X and Y are discrete or when X and Y are continuous. If the conditions are not satisfied for all (x, y) then X and Y are dependent. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

More Than Two Random Variables If X 1, X 2, …, Xn are all discrete random variables, the joint pmf of the variables is the function If the variables are continuous, the joint pdf is the function f such that for any n intervals [a 1, b 1], …, [an, bn], Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Independence – More Than Two Random Variables The random variables X 1, X 2, …, Xn are independent if for every subset of the variables, the joint pmf or pdf of the subset is equal to the product of the marginal pmf’s or pdf’s. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Conditional Probability Function Let X and Y be two continuous rv’s with joint pdf f (x, y) and marginal X pdf f. X(x). Then for any X value x for which f. X(x) > 0, the conditional probability density function of Y given that X = x is If X and Y are discrete, replacing pdf’s by pmf’s gives the conditional probability mass function of Y when X = x. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

5. 2 Expected Values, Covariance, and Correlation Copyright (c) 2004 Brooks/Cole, a division of

Expected Value Let X and Y be jointly distributed rv’s with pmf p(x, y) or pdf f (x, y) according to whether the variables are discrete or continuous. Then the expected value of a function h(X, Y), denoted E[h(X, Y)] or is discrete continuous Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Covariance The covariance between two rv’s X and Y is discrete continuous Copyright (c)

Short-cut Formula for Covariance Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Correlation The correlation coefficient of X and Y, denoted by Corr(X, Y), defined by

Correlation Proposition 1. If a and c are either both positive or both negative, Corr(a. X + b, c. Y + d) = Corr(X, Y) 2. For any two rv’s X and Y, Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Correlation Proposition 1. If X and Y are independent, then but does not imply

5. 3 Statistics and their Distributions Copyright (c) 2004 Brooks/Cole, a division of Thomson

Statistic A statistic is any quantity whose value can be calculated from sample data. Prior to obtaining data, there is uncertainty as to what value of any particular statistic will result. A statistic is a random variable denoted by an uppercase letter; a lowercase letter is used to represent the calculated or observed value of the statistic. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Random Samples The rv’s X 1, …, Xn are said to form a (simple random sample of size n if 1. The Xi’s are independent rv’s. 2. Every Xi has the same probability distribution. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Simulation Experiments The following characteristics must be specified: 1. The statistic of interest. 2. The population distribution. 3. The sample size n. 4. The number of replications k. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

5. 4 The Distribution of the Sample Mean Copyright (c) 2004 Brooks/Cole, a division

Using the Sample Mean Let X 1, …, Xn be a random sample from a distribution with mean value and standard deviation Then In addition, with To = X 1 +…+ Xn, Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Normal Population Distribution Let X 1, …, Xn be a random sample from a normal distribution with mean value and standard deviation Then for any n, is normally distributed, as is To. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

The Central Limit Theorem Let X 1, …, Xn be a random sample from a distribution with mean value and variance Then if n sufficiently large, has approximately a normal distribution with and To also has approximately a normal distribution with The larger the value of n, the better the approximation. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

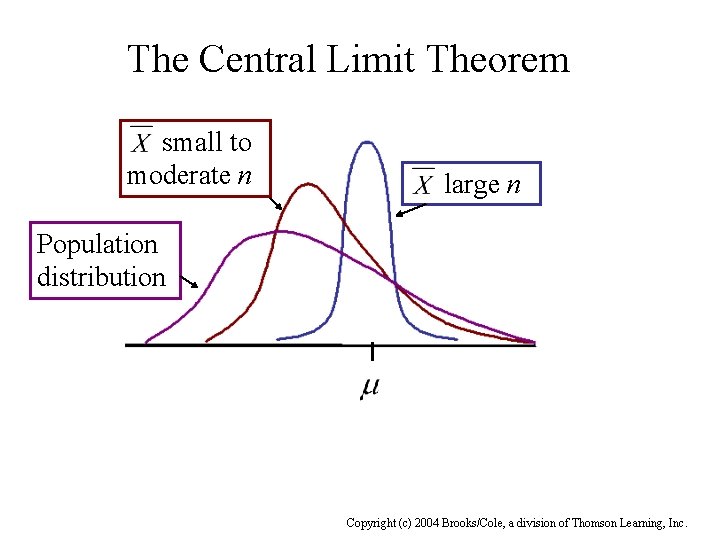
The Central Limit Theorem small to moderate n large n Population distribution Copyright (c)

Rule of Thumb If n > 30, the Central Limit Theorem can be used.

Approximate Lognormal Distribution Let X 1, …, Xn be a random sample from a distribution for which only positive values are possible [P(Xi > 0) = 1]. Then if n is sufficiently large, the product Y = X 1 X 2…Xn has approximately a lognormal distribution. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

5. 5 The Distribution of a Linear Combination Copyright (c) 2004 Brooks/Cole, a division

Linear Combination Given a collection of n random variables X 1, …, Xn and n numerical constants a 1, …, an, the rv is called a linear combination of the Xi’s. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Expected Value of a Linear Combination Let X 1, …, Xn have mean values and variances of respectively Whether or not the Xi’s are independent, Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.

Variance of a Linear Combination If X 1, …, Xn are independent, and Copyright

Variance of a Linear Combination For any X 1, …, Xn, Copyright (c) 2004

Difference Between Two Random Variables and, if X 1 and X 2 are independent,

Difference Between Normal Random Variables If X 1, X 2, …Xn are independent, normally distributed rv’s, then any linear combination of the Xi’s also has a normal distribution. The difference X 1 – X 2 between two independent, normally distributed variables is itself normally distributed. Copyright (c) 2004 Brooks/Cole, a division of Thomson Learning, Inc.