Chapter 5 INTEGRALS Introduction to Integration Area and

Chapter 5. INTEGRALS Introduction to Integration Area and Definite Integral

5. 1 Area problem • We know how to compute areas of rectilinear objects, such as rectangles, triangles, polygons • How do we define and compute areas of more complicated regions (e. g. area enclosed by a circle)? • Idea: approximate such regions by rectilinear regions (for example, by polygons)

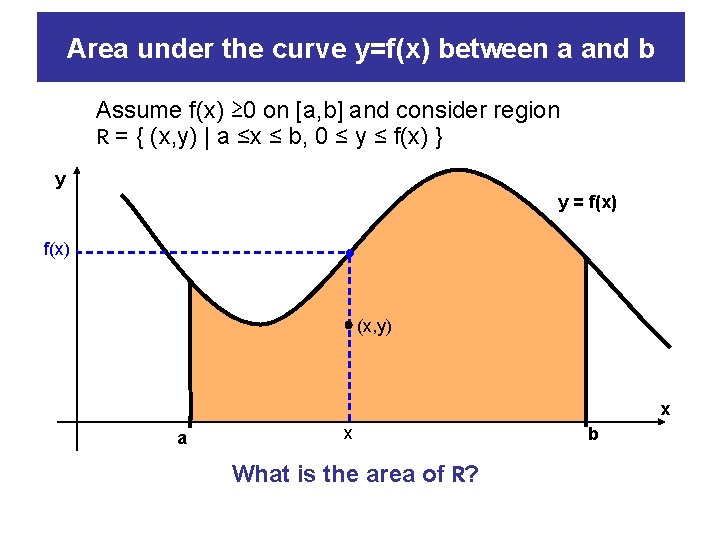
Area under the curve y=f(x) between a and b Assume f(x) ≥ 0 on [a, b] and consider region R = { (x, y) | a ≤x ≤ b, 0 ≤ y ≤ f(x) } y y = f(x) (x, y) x a x What is the area of R? b

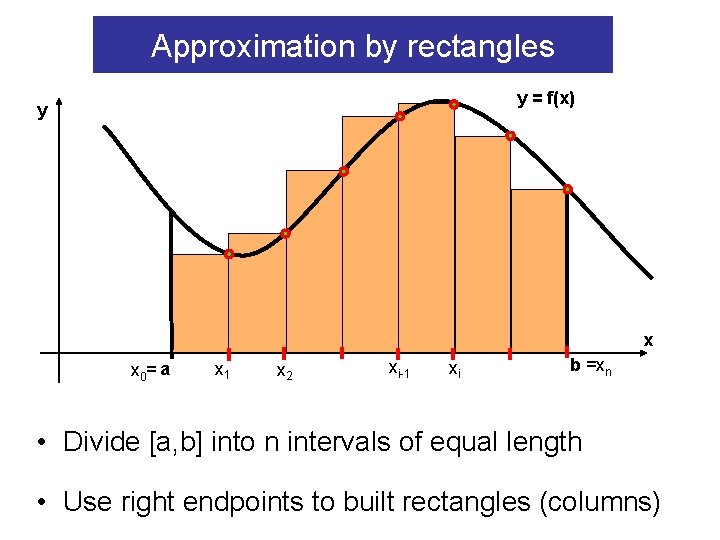
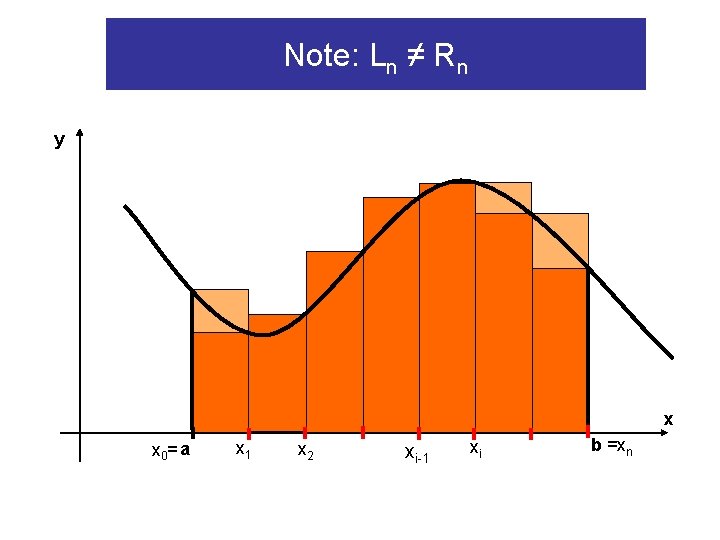
Approximation by rectangles y = f(x) y x x 0= a x 1 x 2 xi-1 xi b =xn • Divide [a, b] into n intervals of equal length • Use right endpoints to built rectangles (columns)

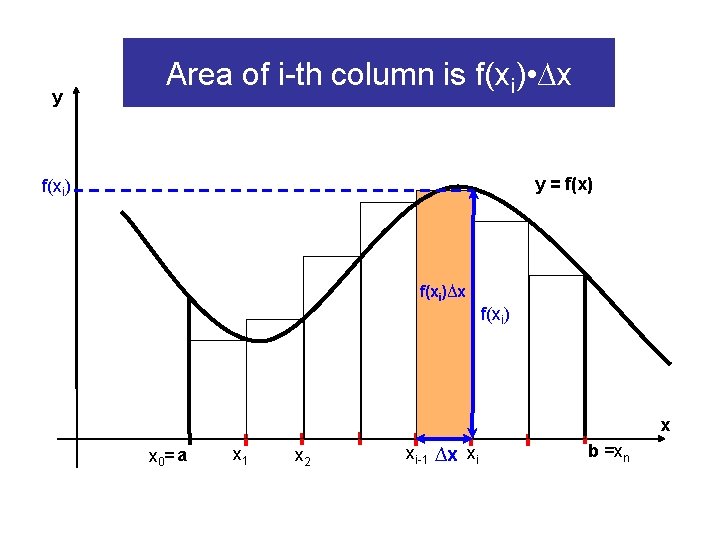
y Area of i-th column is f(xi) • ∆x y = f(x) f(xi)∆x f(xi) x x 0= a x 1 x 2 xi-1 ∆x xi b =xn

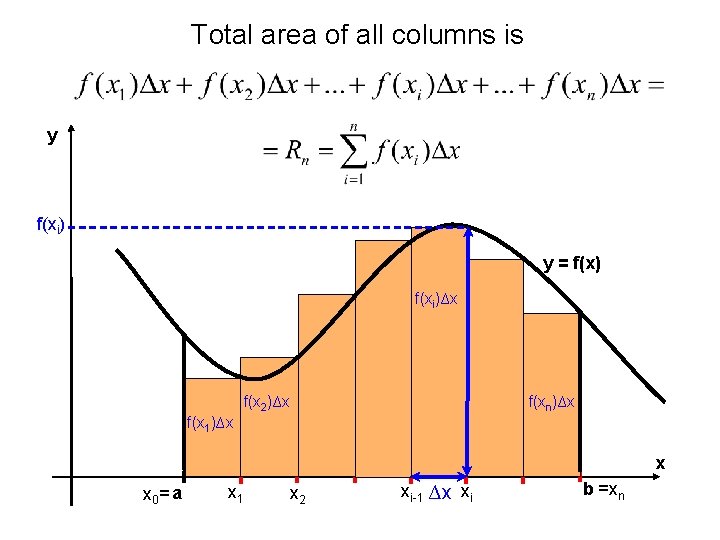
Total area of all columns is y f(xi) y = f(x) f(xi)∆x f(x 1)∆x f(xn)∆x f(x 2)∆x x x 0= a x 1 x 2 xi-1 ∆x xi b =xn

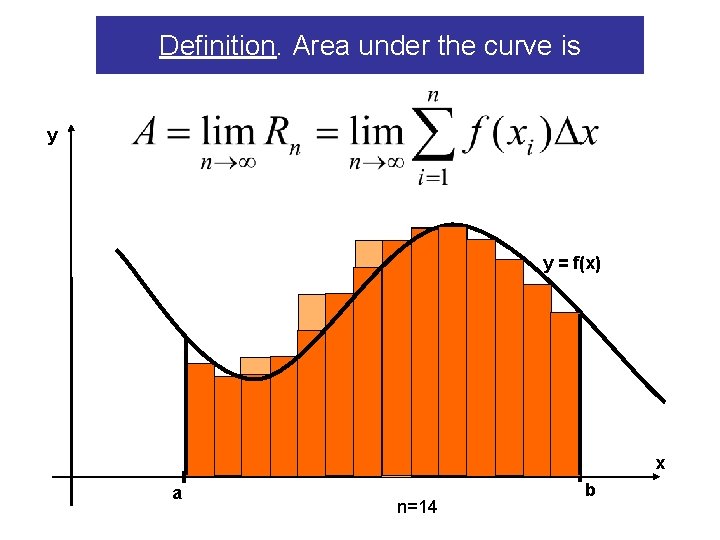
Definition. Area under the curve is y y = f(x) x a n=14 b

Theorem. If f is continuous on [a, b] then the following limit exists: y y = f(x) x a b

How to find xi ∆x x 0= a ∆x ∆x x 1 x 2 xi-1 x xi b =xn

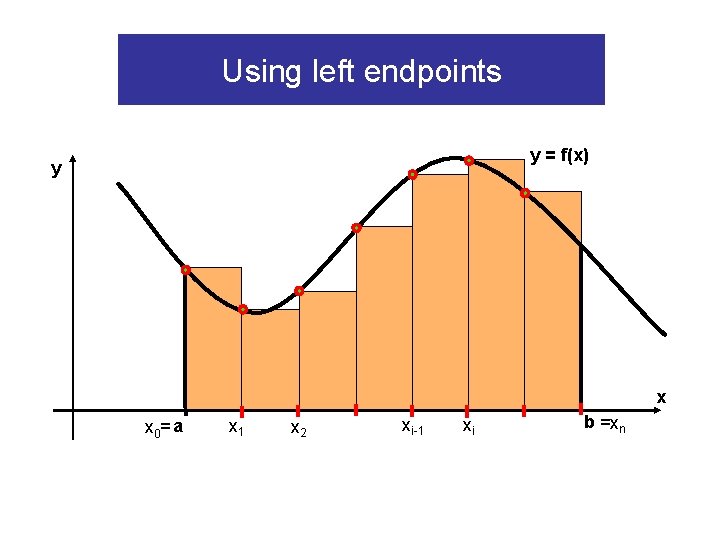
Using left endpoints y = f(x) y x x 0= a x 1 x 2 xi-1 xi b =xn

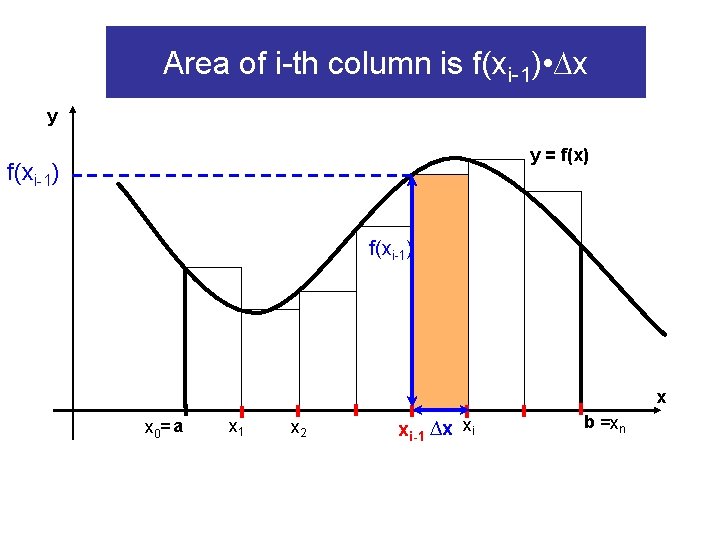
Area of i-th column is f(xi-1) • ∆x y y = f(x) f(xi-1) x x 0= a x 1 x 2 xi-1 ∆x xi b =xn

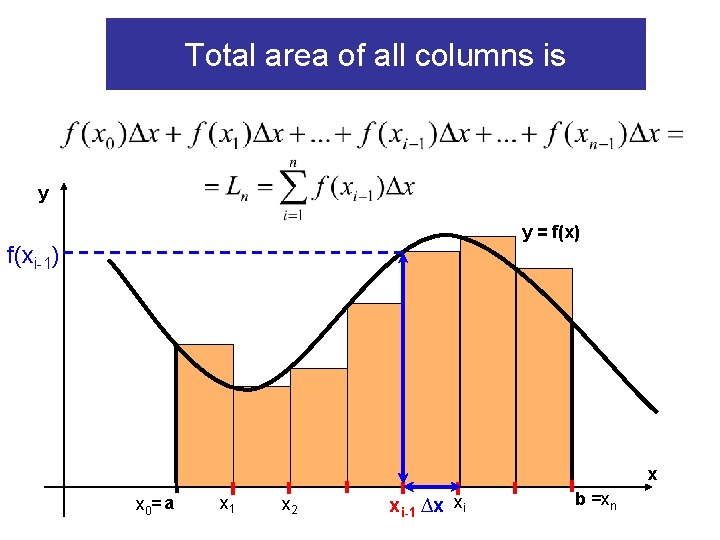
Total area of all columns is y y = f(x) f(xi-1) x x 0= a x 1 x 2 xi-1 ∆x xi b =xn

Note: Ln ≠ Rn y x x 0= a x 1 x 2 xi-1 xi b =xn

Nevertheless… • Theorem. If f(x) is continuous on [a, b], then both limits and exist and

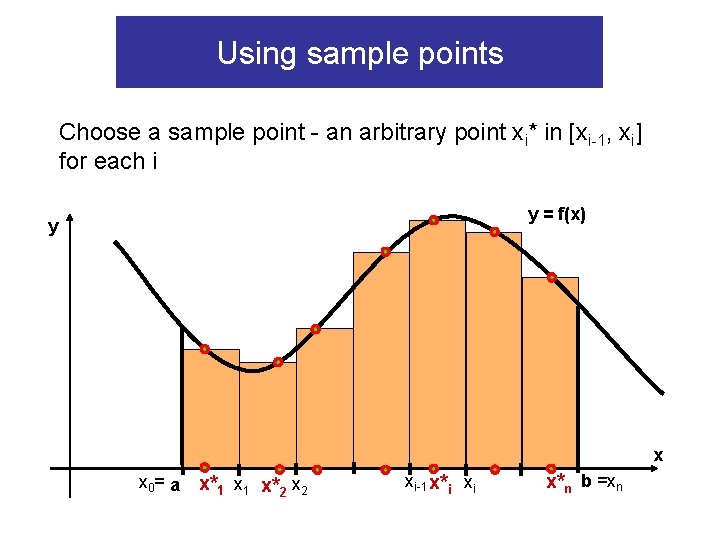
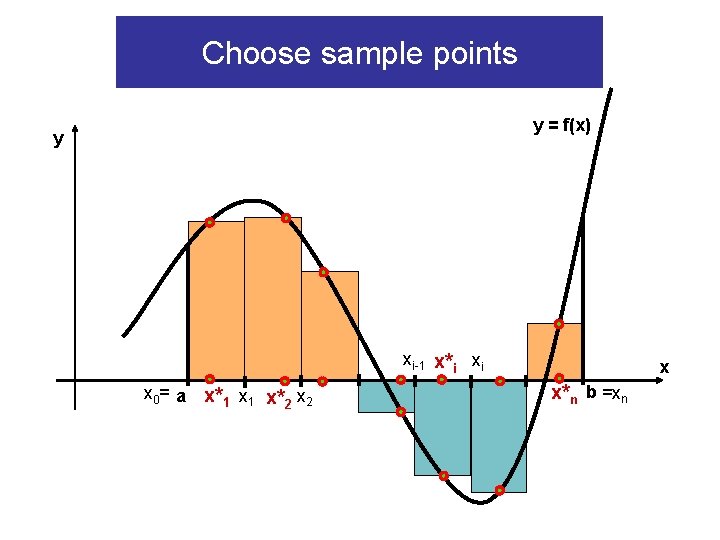
Using sample points Choose a sample point - an arbitrary point xi* in [xi-1, xi] for each i y = f(x) y x x 0= a x*1 x 1 x*2 x 2 xi-1 x*i xi x*n b =xn

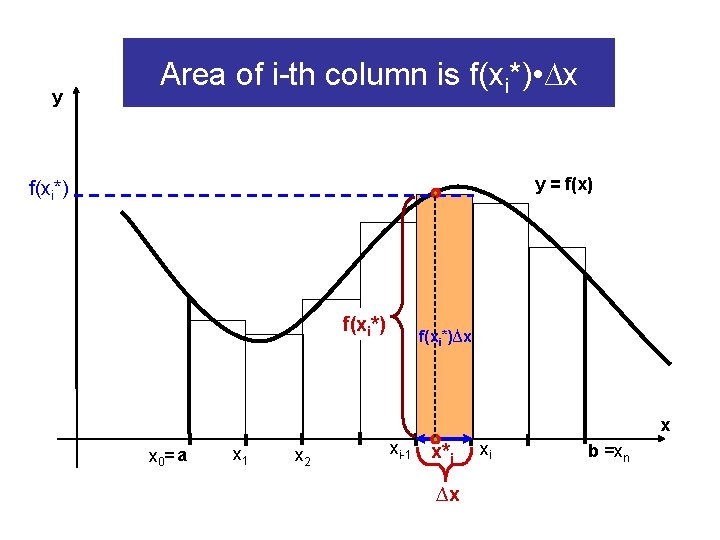
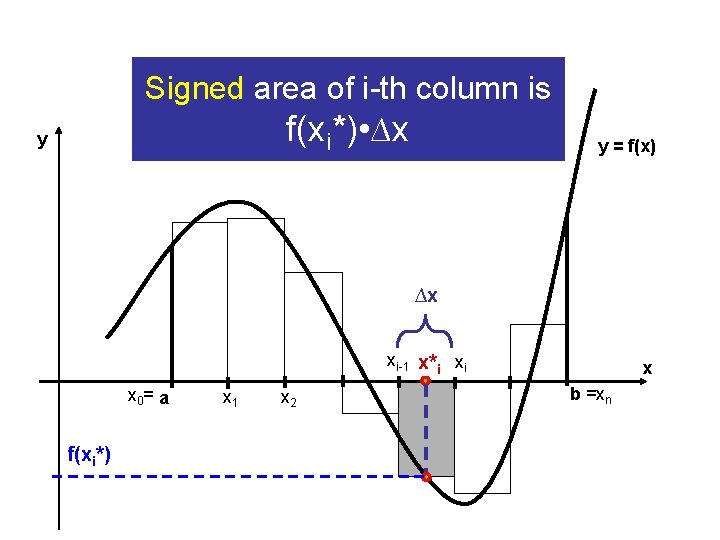
y Area of i-th column is f(xi*) • ∆x y = f(x) f(xi*)∆x x x 0= a x 1 x 2 xi-1 x*i ∆x xi b =xn

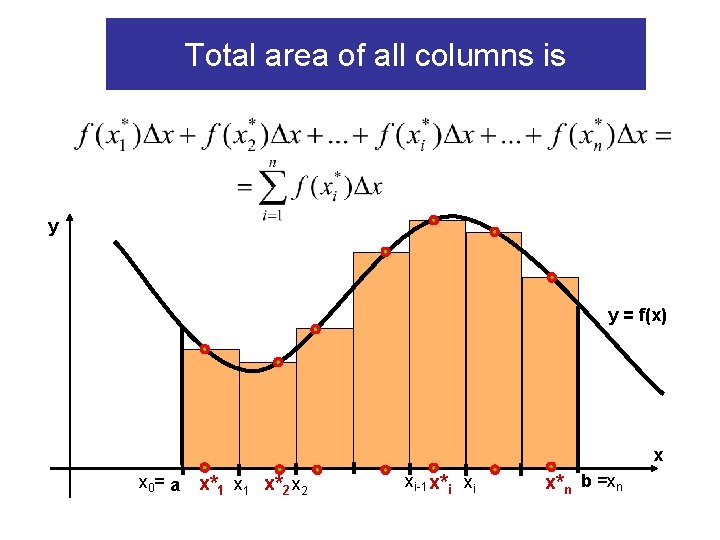
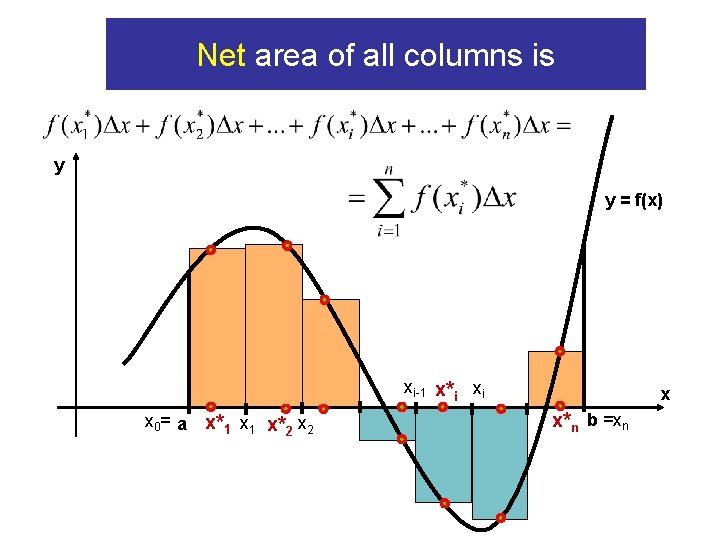
Total area of all columns is y y = f(x) x x 0= a x*1 x 1 x*2 x 2 xi-1 x*i xi x*n b =xn

Theorem • If f(x) is continuous on [a, b], then the limit exists and does not depend on the choice of sample points

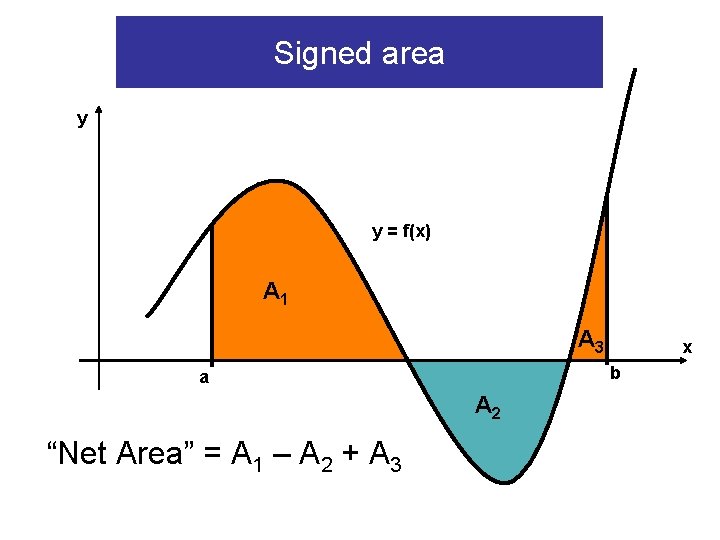
5. 2 Definite Integral • Now we consider functions that may change sign on [a, b] • In this case, we need to take into account sign of f(x) • Idea: use “signed area”

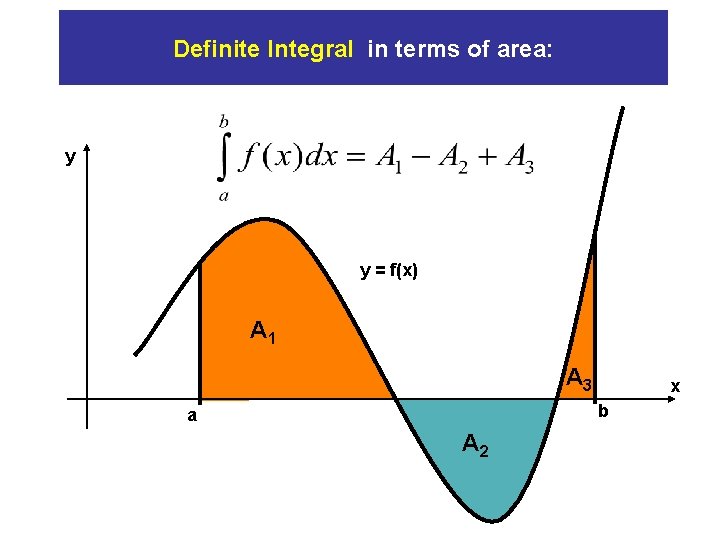
Signed area y y = f(x) A 1 A 3 b a A 2 “Net Area” = A 1 – A 2 + A 3 x

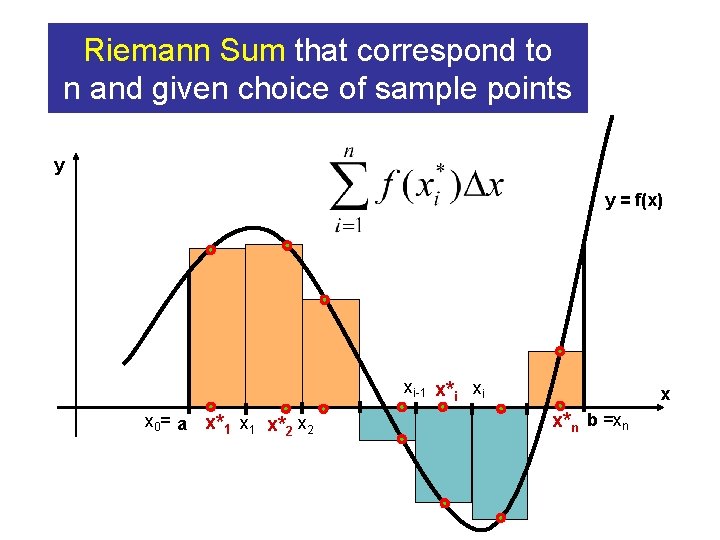
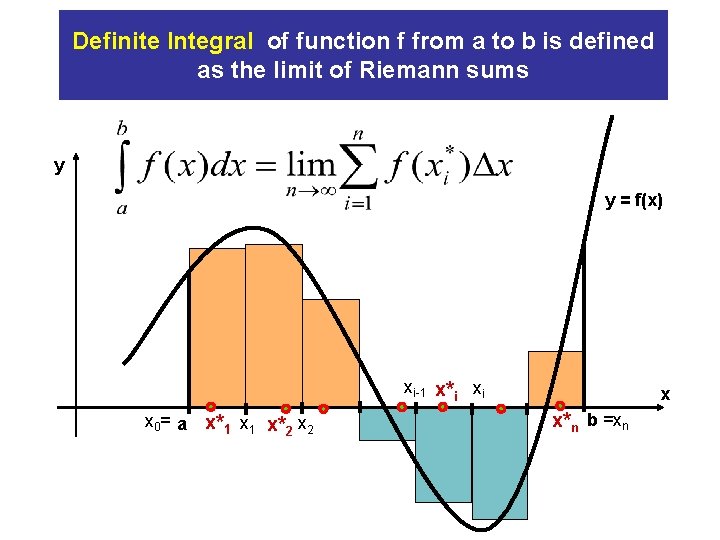
Choose sample points y = f(x) y xi-1 x*i xi x 0= a x*1 x 1 x*2 x x*n b =xn

Signed area of i-th column is f(xi*) • ∆x y y = f(x) ∆x xi-1 x*i xi x 0= a f(xi*) x 1 x 2 x b =xn

Net area of all columns is y y = f(x) xi-1 x*i xi x 0= a x*1 x 1 x*2 x x*n b =xn

Riemann Sum that correspond to n and given choice of sample points y y = f(x) xi-1 x*i xi x 0= a x*1 x 1 x*2 x x*n b =xn

Definite Integral of function f from a to b is defined as the limit of Riemann sums y y = f(x) xi-1 x*i xi x 0= a x*1 x 1 x*2 x x*n b =xn

Theorem • If f(x) is continuous on [a, b], then the definite integral of function f from a to b exists and does not depend on the choice of sample points

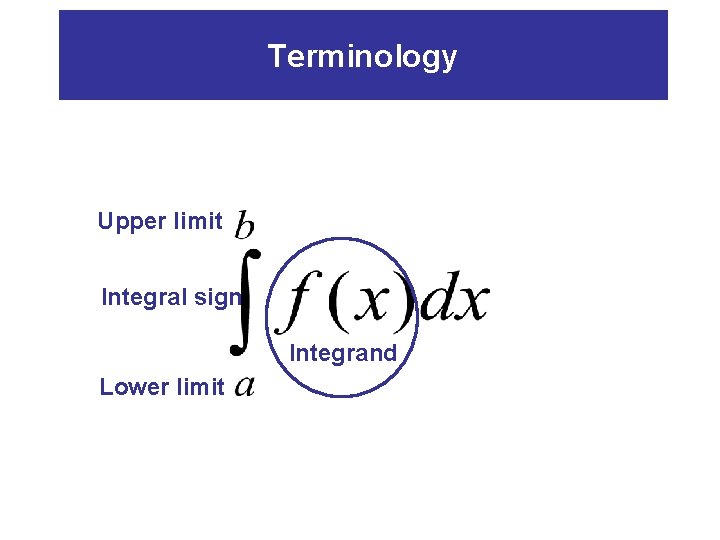
Terminology Upper limit Integral sign Integrand Lower limit

Definite Integral in terms of area: y y = f(x) A 1 A 3 x b a A 2