Chapter 5 How the spectrometer works 5 1




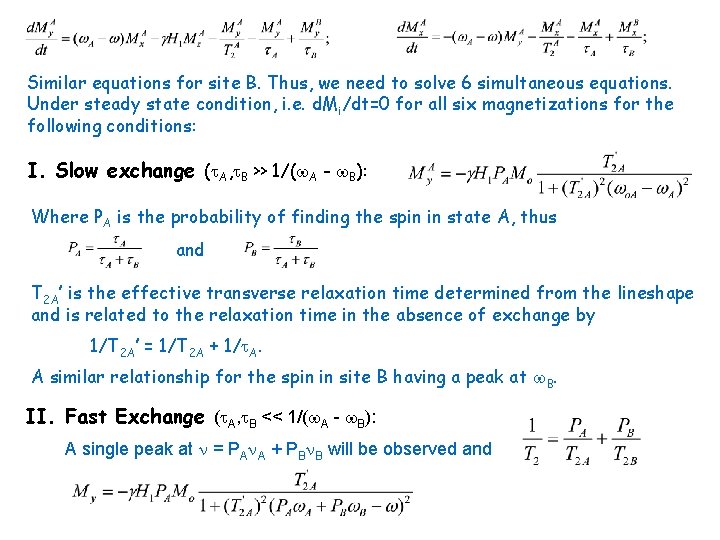


- Slides: 15

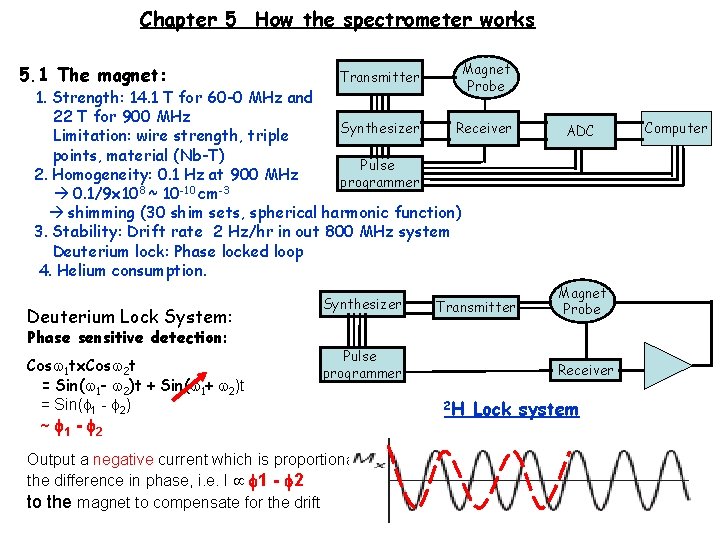
Chapter 5 How the spectrometer works 5. 1 The magnet: Transmitter Magnet Probe 1. Strength: 14. 1 T for 60 -0 MHz and 22 T for 900 MHz Synthesizer Receiver Limitation: wire strength, triple points, material (Nb-T) Pulse 2. Homogeneity: 0. 1 Hz at 900 MHz programmer 0. 1/9 x 108 ~ 10 -10 cm-3 shimming (30 shim sets, spherical harmonic function) 3. Stability: Drift rate 2 Hz/hr in out 800 MHz system Deuterium lock: Phase locked loop 4. Helium consumption. Deuterium Lock System: Phase sensitive detection: Cos 1 tx. Cos 2 t = Sin( 1 - 2)t + Sin( 1+ 2)t = Sin( 1 - 2) ~ 1 - 2 Synthesizer Transmitter Pulse programmer Output a negative current which is proportional to the difference in phase, i. e. I 1 - 2 to the magnet to compensate for the drift ADC Magnet Probe Receiver 2 H Lock system Computer

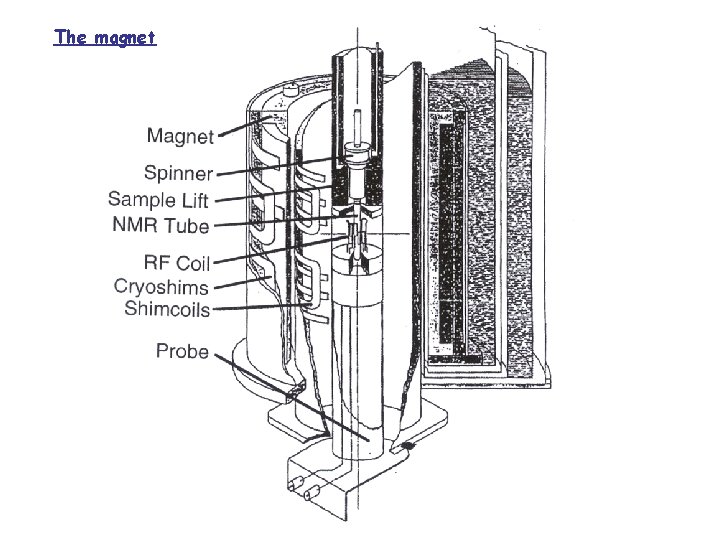
The magnet

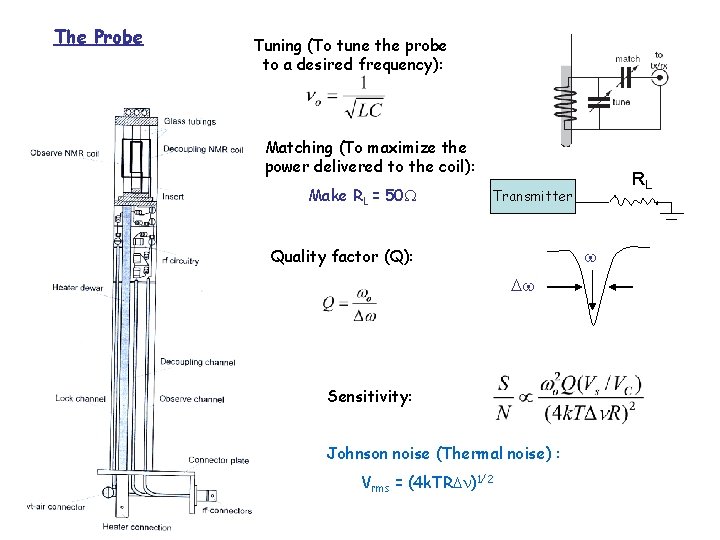
The Probe Tuning (To tune the probe to a desired frequency): Matching (To maximize the power delivered to the coil): Make RL = 50 RL Transmitter Quality factor (Q): Sensitivity: Johnson noise (Thermal noise) : Vrms = (4 k. TR )1/2

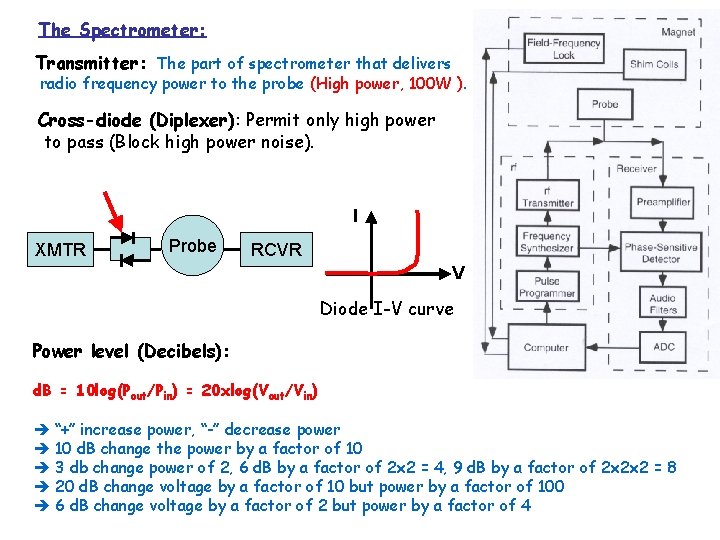
The Spectrometer: Transmitter: The part of spectrometer that delivers radio frequency power to the probe (High power, 100 W ). Cross-diode (Diplexer): Permit only high power to pass (Block high power noise). I XMTR Probe RCVR V Diode I-V curve Power level (Decibels): d. B = 10 log(Pout/Pin) = 20 xlog(Vout/Vin) “+” increase power, “-” decrease power 10 d. B change the power by a factor of 10 3 db change power of 2, 6 d. B by a factor of 2 x 2 = 4, 9 d. B by a factor of 2 x 2 x 2 = 8 20 d. B change voltage by a factor of 10 but power by a factor of 100 6 d. B change voltage by a factor of 2 but power by a factor of 4

Power level and pulse width: How many d. B do you have to use for increasing the pulse width by a factor of 2 (Assuming a linear amplifier is use, class C amplifier) ? . Pulse width i (power)1/2 Increase pulse width by a factor of 2 need to decrease power by 4. d. B = 10 log 4 ~ - 6 d. B In general: Power ratio in d. B = 20 log 10( initial/ new) If the current 90 o pulse is i = 10 us how do we adjust attenuator in order to get a 90 o pulse of new = 8 us ? Ans: d. B = 20 log (10/8) = 1. 9 d. B One needs to reduce the attenuator by 1. 9 d. B, i. e. if the initial attenuation was set at 12 d. B then for getting a 8 us 90 o pulse the new attenuation should be set at 10. 1 d. B. Phase: X-pulse (0 o phase-shifted, 90 X, a cosine wave) Y-pulse (90 o phase-shifted, 90 Y, a sine wave)

Receiver: The part of spectrometer that detect and Amplifies signal (Low power, u. V) Need to amplify by a factor of 106 1. 0 V 120 d. B amplification The first stage of amplification is the most important Preamplifier (Preamp) determines the receiver S/N ratio. Broad band Ga. As amplifier is used (Noise figure ~ 1. 04 d. B) - 1. 0 V Digitizing the signal (Analog to Digital Converter, ADC): A device which convert analog signal voltage into digital numbers. Factors to be considered in choosing a ADC: 1. 0 V 1. Resolution (How many “bits“): A n-bit ADC divide the full 2. analog voltage into 2 N divisions. A 10 -bit ADC convert the 3. 1. 0 V signal into 210 = 1024 division 4. Minimum signal that can be detected = 1/1024 ~ 1 m. V. - 1. 0 V 5. Signal below 1 m. V will be treated as noise. 6. Set receiver gain as high as possible without saturation. 7. 2. Speed (Sampling rate): 3. Nyquist theorem: One need at least two points per cycle to correctly represent 4. a sinusoidal wave. 5. Sampling rate must be at least twice the spectral width to be covered. 6. Dwell time 1/fmax. For example to observe a signal which resonates at 1 k. Hz one 7. needs to digitize at 2 k. Hz rate or DW = 1/2000 = 0. 5 ms. But since in quadrature 8. detection one can see both +fmax and –fmax one is able to observe 2 fmax range.

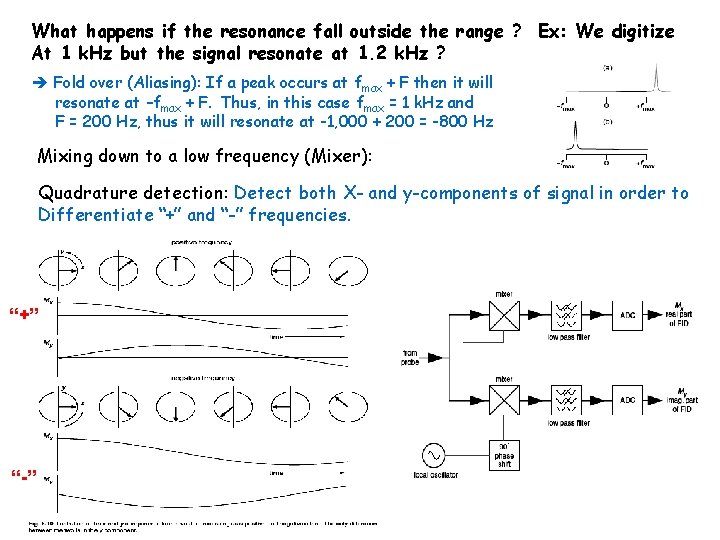
What happens if the resonance fall outside the range ? Ex: We digitize At 1 k. Hz but the signal resonate at 1. 2 k. Hz ? Fold over (Aliasing): If a peak occurs at fmax + F then it will resonate at –fmax + F. Thus, in this case fmax = 1 k. Hz and F = 200 Hz, thus it will resonate at -1, 000 + 200 = -800 Hz Mixing down to a low frequency (Mixer): Quadrature detection: Detect both X- and y-components of signal in order to Differentiate “+” and “-” frequencies. “+” “-”

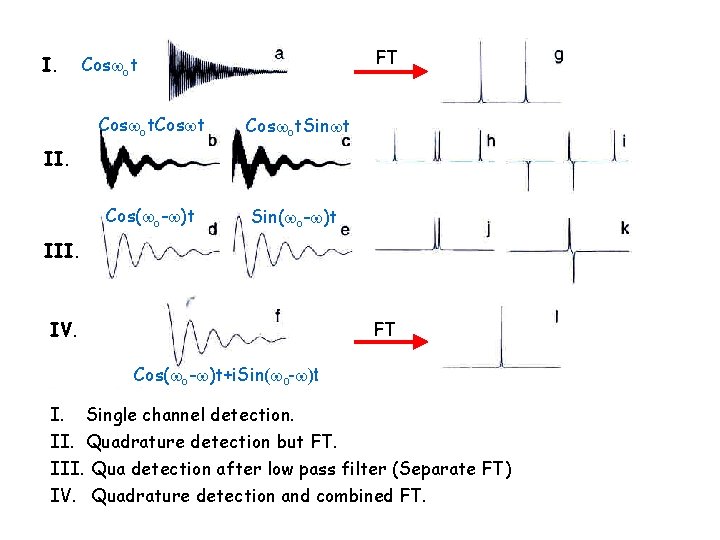
Quadrature detection: Mixing of two RF signals, Cos ot and Cos rxt, where o is the Larmor frequency and rx is the reference frequency, we obtain: ACos ot x Cos rxt = ½A[Cos( o + rx)t + Cos( o - rx)t] ---- (1) Similarly, mixing of Cos ot with -Sin rxt we obtain: ACos ot x (-Sin rxt) = ½A[-Sin( o + rx)t + Sin( o - rx)t] ----- (2) After low pass filter only the low frequency component is detected. Thus, we see only Cos( o - rx) for eq. 1 and Sin( o - rx) for eq. 2. By shifting the receiver phase by 90 o we can detect either Xor Y-component of the signal. If we then recombine eq. 1 and 2 we obtain: Signal = ½A[Cos ( o + rx)t + Sin ( o - rx)t ] = ½ A exp[-i( o + rx)t] We can differentiate whether ( o - rx) is “+” or “-”. It increases sensitivity by a factor of (2)1/2 or 1. 414. Dwell time (1/digitization rate) and spectral width: For obtaining a spectral width, fsw (or from - ½fsw to ½fsw) one need to digitize at the same frequency with a dwell time = 1/fsw.

I. FT Cos ot. Cos t Cos ot. Sin t Cos( o- )t Sin( o- )t II. III. FT IV. Cos( o- )t+i. Sin( o- )t I. Single channel detection. II. Quadrature detection but FT. III. Qua detection after low pass filter (Separate FT) IV. Quadrature detection and combined FT.

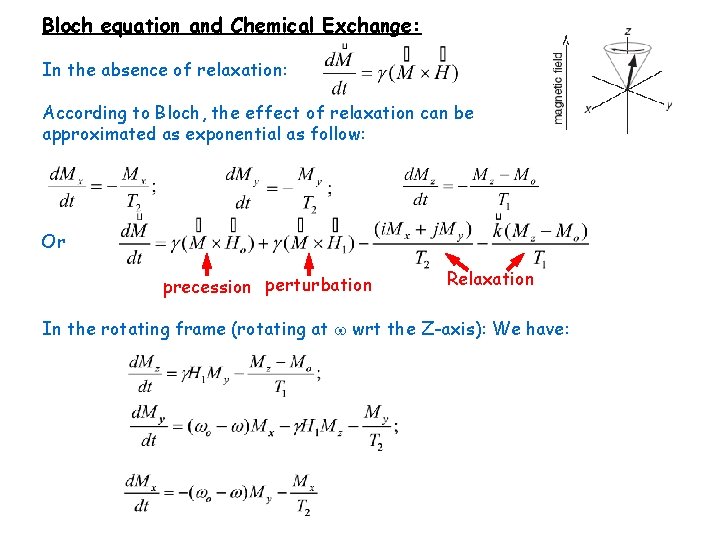
Bloch equation and Chemical Exchange: In the absence of relaxation: According to Bloch, the effect of relaxation can be approximated as exponential as follow: Or precession perturbation Relaxation In the rotating frame (rotating at wrt the Z-axis): We have:

Solution to the Bloch equation: Under steady state condition: d. Mx/dt =d. My/dt = d. Mz/dt = 0 we can solve the equations and the following results: My (Absorption) (Dispersion) Mx For a small H 1 field, i. e. 2 H 12 T 1 T 2 <<1 we have: (Lorentzian) Two-site Chemical Exchange: A 1/ B B For a spin exchange in two magnetically different environments A and B having chemical shift A/2 and B/2 and life time A and B. Bloch equations become:
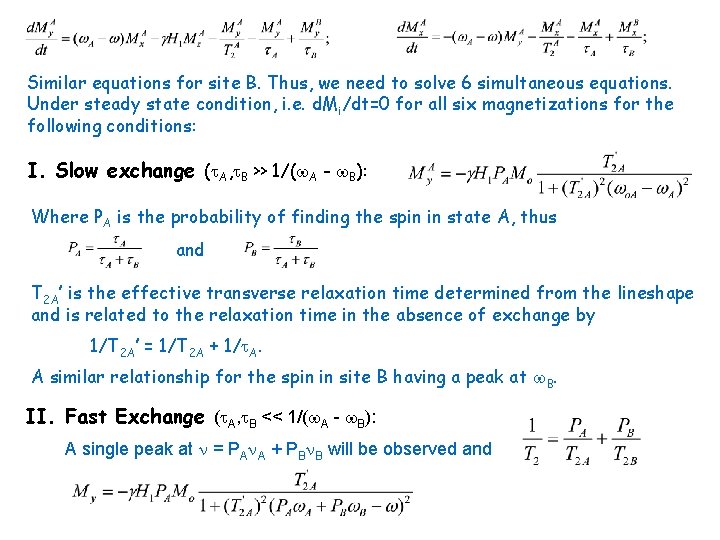
Similar equations for site B. Thus, we need to solve 6 simultaneous equations. Under steady state condition, i. e. d. Mi/dt=0 for all six magnetizations for the following conditions: I. Slow exchange ( A, B >> 1/( A - B): Where PA is the probability of finding the spin in state A, thus and T 2 A’ is the effective transverse relaxation time determined from the lineshape and is related to the relaxation time in the absence of exchange by 1/T 2 A’ = 1/T 2 A + 1/ A. A similar relationship for the spin in site B having a peak at B. II. Fast Exchange ( A, B << 1/( A - B): A single peak at = PA A + PB B will be observed and

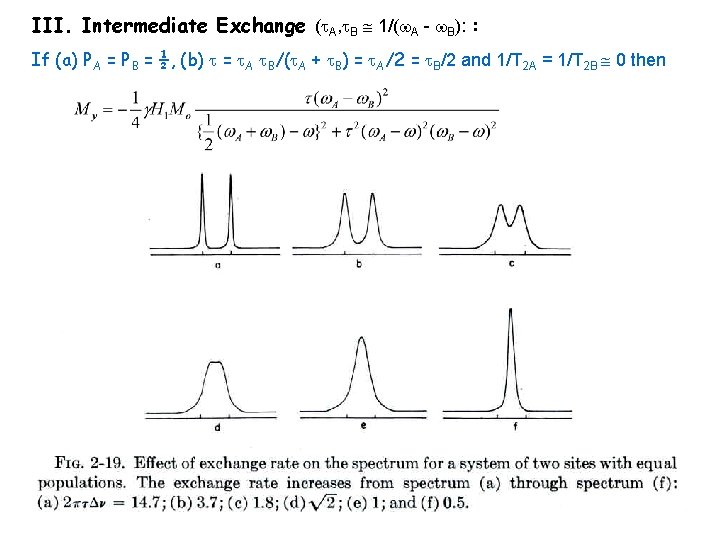
III. Intermediate Exchange ( A, B 1/( A - B): : If (a) PA = PB = ½, (b) = A B/( A + B) = A/2 = B/2 and 1/T 2 A = 1/T 2 B 0 then

