Chapter 5 General Linear List Internet Computing Laboratory

Chapter 5. General Linear List Internet Computing Laboratory @ KUT Youn-Hee Han
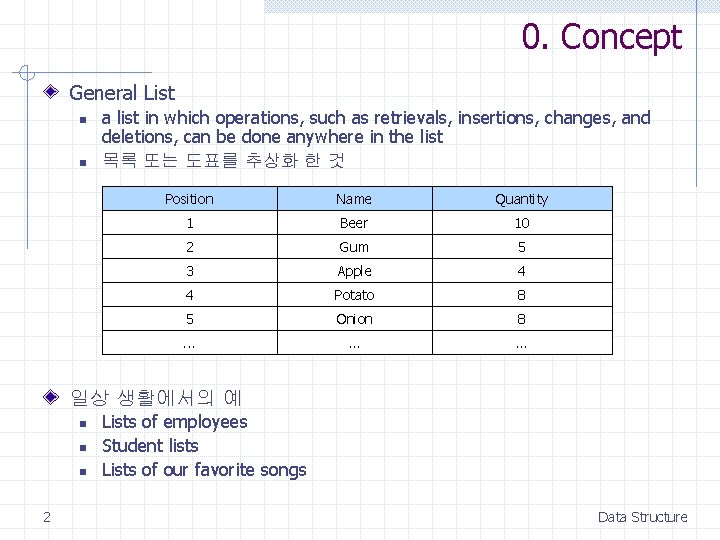
0. Concept General List n n a list in which operations, such as retrievals, insertions, changes, and deletions, can be done anywhere in the list 목록 또는 도표를 추상화 한 것 Position Name Quantity 1 Beer 10 2 Gum 5 3 Apple 4 4 Potato 8 5 Onion 8 . . 일상 생활에서의 예 n n n 2 Lists of employees Student lists Lists of our favorite songs Data Structure

0. Concept 필요한 연산은? n n n 주 연산: insertion, deletion, retrieval, traversal 보조 연산: … 그렇다면, insertion에 대해서 다음 중 어떤 것을 제공해야 하는가? 사용자는 어떤 것을 더 원하는가? 둘 다 원하는가? w insert (data) w insert (position, data) Position-oriented List (위치 기반 리스트) 에서의 연산 정의 예 n insert(position, data) w 데이터를 주어진 위치(position)에 넣기 n delete(position) w 주어진 위치(position)의 데이터를 삭제 n retrieve(position, &data) position name quantity 1 Beer 10 2 Gum 5 3 Apple 4 . . w 주어진 위치(position)의 데이터를 Data 변수에 복사 n traversal w 리스트 안에 모든 Element에 대해 순서대로 일정한 작업 (예를 들어 단순 방문) 을 행한 다. 3 Data Structure
1. Basic Operations Insertion n In ordered list: maintained in sequence according to data w Key: one or more field that identifies the data (ex: SSN) Deletion n 5 Deletion requires search to locate the data to delete Data Structure
1. Basic Operations Retrieval n provides a data without changing list n Search: finding an element in a list by some key Traversal n process of visiting each element in a list in sequence to do something w Ex) print all elements in a list n 6 Requires looping for all elements Data Structure
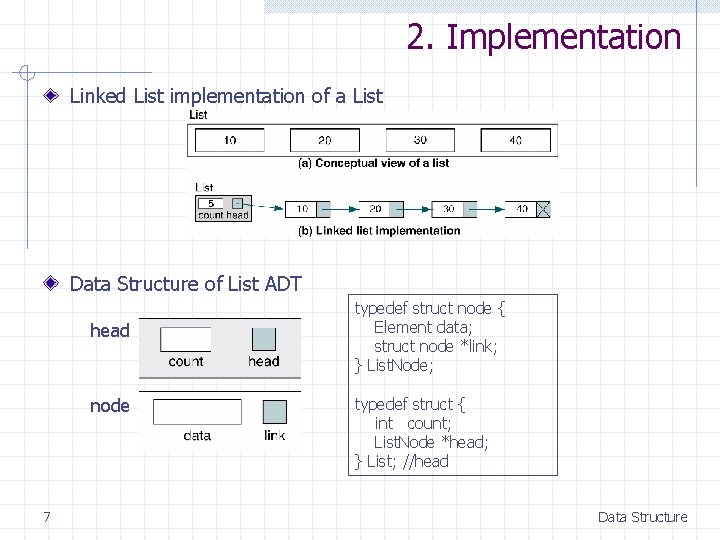
2. Implementation Linked List implementation of a List Data Structure of List ADT head node 7 typedef struct node { Element data; struct node *link; } List. Node; typedef struct { int count; List. Node *head; } List; //head Data Structure
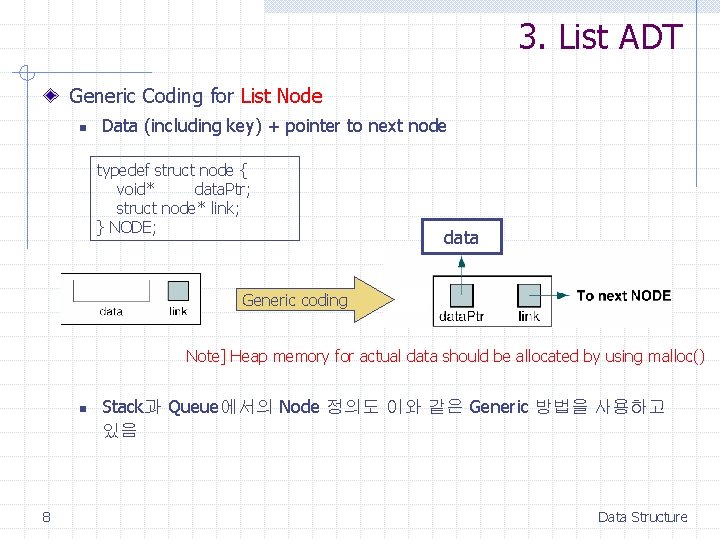
3. List ADT Generic Coding for List Node n Data (including key) + pointer to next node typedef struct node { void* data. Ptr; struct node* link; } NODE; data Generic coding Note] Heap memory for actual data should be allocated by using malloc() n 8 Stack과 Queue에서의 Node 정의도 이와 같은 Generic 방법을 사용하고 있음 Data Structure
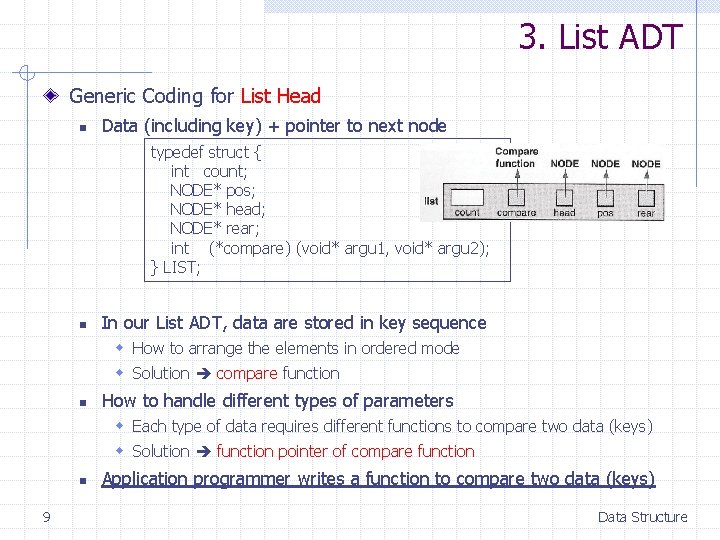
3. List ADT Generic Coding for List Head n Data (including key) + pointer to next node typedef struct { int count; NODE* pos; NODE* head; NODE* rear; int (*compare) (void* argu 1, void* argu 2); } LIST; n In our List ADT, data are stored in key sequence w How to arrange the elements in ordered mode w Solution compare function n How to handle different types of parameters w Each type of data requires different functions to compare two data (keys) w Solution function pointer of compare function n 9 Application programmer writes a function to compare two data (keys) Data Structure

3. List ADT Generic Coding for List Head n int (*compare) (void* argu 1, void* argu 2); w 본 교재에서는 다음과 같이 return 값이 정의됨 n n Case I) argu 1 의 데이터 > argu 2 의 데이터 1 이 리턴됨 n Case II) argu 1 의 데이터 < argu 2 의 데이터 -1 이 리턴됨 n Case III) argu 1 의 데이터 == argu 2 의 데이터 0 이 리턴됨 Examples int compare. Int(void *argu 1, void *argu 2) { return *(int*)argu 1 - *(int*)argu 2; } int compare. Str(void *argu 1, void *argu 2) { return strcmp((char*)argu 1, (char*)argu 2); } 10 Data Structure

3. List ADT Header file with List ADT Prototypes n File Name: list. h (이후 모든 ADT 구현은 이 한 파일에 추가) typedef struct node { void* data. Ptr; struct node* link; } NODE; typedef struct { int count; NODE* pos; NODE* head; NODE* rear; int (*compare) (void* argu 1, void* argu 2); } LIST; LIST* create. List (int (*compare) (void* argu 1, void* argu 2)); LIST* destroy. List (LIST* list); 11 Data Structure

3. List ADT Header file with List ADT Prototypes int add. Node (LIST* p. List, void* data. In. Ptr); bool remove. Node (LIST* p. List, void* key. Ptr, void** data. Out. Ptr); bool search. List (LIST* p. List, void* p. Argu, void** p. Data. Out); bool retrieve. Node (LIST* p. List, void* p. Argu, void** data. Out. Ptr); bool traverse (LIST* p. List, int from. Where, void** data. Out. Ptr); int list. Count (LIST* p. List); bool empty. List (LIST* p. List); bool full. List (LIST* p. List); static int _insert (LIST* p. List, NODE* p. Pre, void* data. In. Ptr); static void _delete (LIST* p. List, NODE* p. Pre, NODE* p. Loc, void** data. Out. Ptr); static bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu); 12 Data Structure
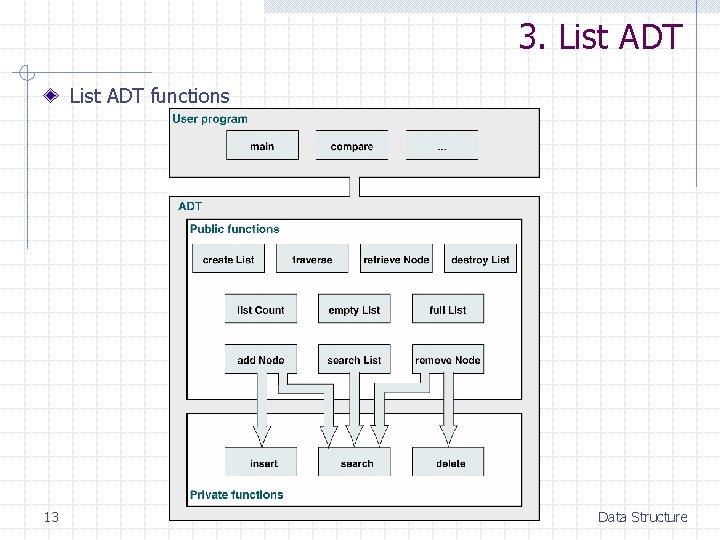
3. List ADT functions 13 Data Structure

3. List ADT create. List n Only parameter is the compare function required to compare two data (keys) LIST* create. List (int (*compare) (void* argu 1, void* argu 2)) { LIST* list; list = (LIST*) malloc (sizeof (LIST)); } 0 if (list) { list->head = NULL; list->pos = NULL; // working pointer for list traversal list->rear = NULL; list->count = 0; list->compare = compare; } return list; In main()… list = create. List (cmp. Year); 14 Data Structure

3. List ADT add. Node n Find the location to insert the node n Directly preceding node is necessary & Insert node after the preceding node int add. Node (LIST* p. List, void* data. In. Ptr) { bool found; bool success; NODE* p. Pre; NODE* p. Loc; found = _search (p. List, &p. Pre, &p. Loc, data. In. Ptr); if (found) return (+1); } 15 Inserting 55 success = _insert (p. List, p. Pre, data. In. Ptr); if (!success) return (-1); p. Pre: data. In. Ptr을 포함하는 NODE가 삽입되어야 return (0); 할 위치 바로 직전의 NODE를 가리키는 포인터 p. Loc: data. In. Ptr과 같은 값을 지니는 NODE가 list 내에 존재할 때 그 NODE를 가리키는 포인터 Data Structure
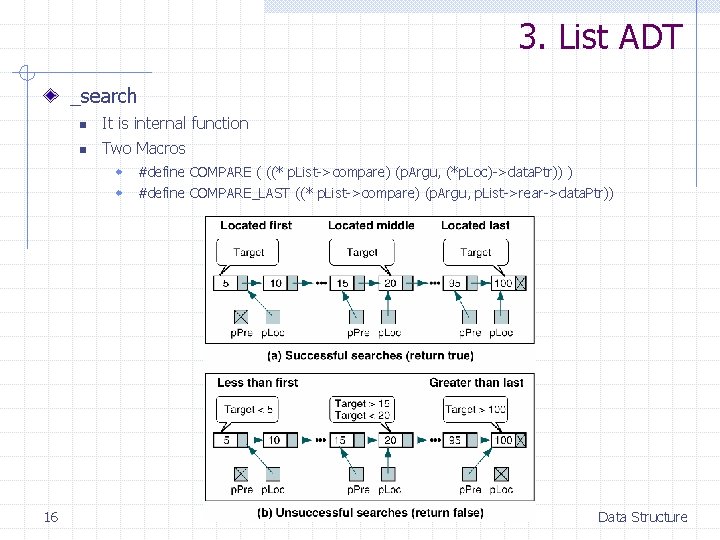
3. List ADT _search 16 n It is internal function n Two Macros w #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) w #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) Data Structure

3. List ADT _search n 17 Case (a) – 1 : 찾는 노드가 리스트의 첫 번째 노드일 때 bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu) { #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) int result; *p. Pre = NULL; *p. Loc = p. List->head; if (p. List->count == 0) return false; } if ( COMPARE_LAST > 0) { p. List *p. Pre = p. List->rear; *p. Loc = NULL; return false; } while ( (result = COMPARE) > 0 ) { *p. Pre = *p. Loc; *p. Loc = (*p. Loc)->link; } if (result == 0) return true; else return false; [TABLE 5 -1] Target=first node p. Pre=NULL p. Loc=First node Return is True Data Structure

3. List ADT _search n 18 Case (a) – 2 : 찾는 노드가 리스트의 중간에 위치한 노드일 때 bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu) { #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) int result; *p. Pre = NULL; *p. Loc = p. List->head; if (p. List->count == 0) return false; } if ( COMPARE_LAST > 0) { *p. Pre = p. List->rear; *p. Loc = NULL; return false; } while ( (result = COMPARE) > 0 ) { *p. Pre = *p. Loc; *p. Loc = (*p. Loc)->link; } if (result == 0) return true; else return false; [TABLE 5 -1] Target=middle node p. Pre=Node’s predecessor p. Loc=Equal node (middle node) Return is True Data Structure

3. List ADT _search n 19 Case (a) – 3 : 찾는 노드가 리스트의 마지막 노드일 때 bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu) { #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) int result; *p. Pre = NULL; *p. Loc = p. List->head; if (p. List->count == 0) return false; } if ( COMPARE_LAST > 0) { *p. Pre = p. List->rear; *p. Loc = NULL; return false; } while ( (result = COMPARE) > 0 ) { *p. Pre = *p. Loc; *p. Loc = (*p. Loc)->link; } if (result == 0) return true; else return false; [TABLE 5 -1] Target=last node p. Pre=Last’s predecessor p. Loc=Last node Return is True Data Structure

3. List ADT _search n 20 Case (b) – 1 : 찾는 노드가 리스트의 첫번째 노드 보다 작을 때 bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu) { #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) int result; *p. Pre = NULL; *p. Loc = p. List->head; if (p. List->count == 0) return false; } if ( COMPARE_LAST > 0) { p. List *p. Pre = p. List->rear; *p. Loc = NULL; return false; } while ( (result = COMPARE) > 0 ) { *p. Pre = *p. Loc; *p. Loc = (*p. Loc)->link; } if (result == 0) return true; else return false; [TABLE 5 -1] Target<first node p. Pre=NULL p. Loc=First node Return is False Data Structure
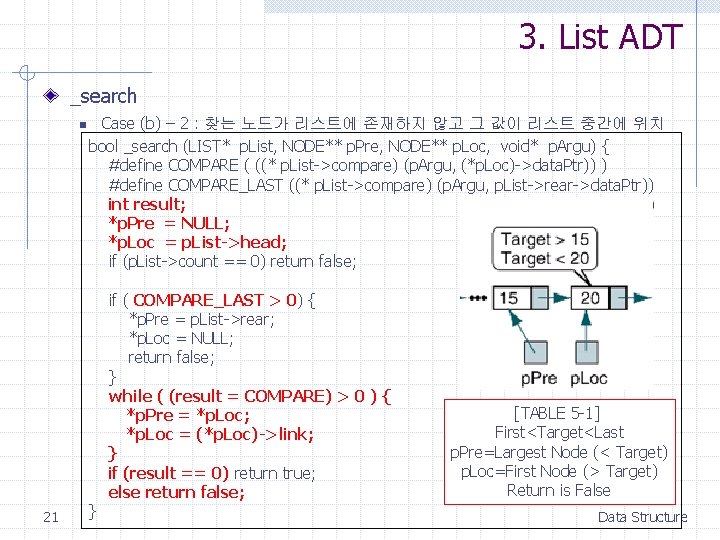
3. List ADT _search n 21 Case (b) – 2 : 찾는 노드가 리스트에 존재하지 않고 그 값이 리스트 중간에 위치 bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu) { #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) int result; *p. Pre = NULL; *p. Loc = p. List->head; if (p. List->count == 0) return false; } if ( COMPARE_LAST > 0) { *p. Pre = p. List->rear; *p. Loc = NULL; return false; } while ( (result = COMPARE) > 0 ) { *p. Pre = *p. Loc; *p. Loc = (*p. Loc)->link; } if (result == 0) return true; else return false; [TABLE 5 -1] First<Target<Last p. Pre=Largest Node (< Target) p. Loc=First Node (> Target) Return is False Data Structure

3. List ADT _search n 22 Case (b) – 3 : 찾는 노드가 리스트의 마지막 노드 보다 더 클 때 bool _search (LIST* p. List, NODE** p. Pre, NODE** p. Loc, void* p. Argu) { #define COMPARE ( ((* p. List->compare) (p. Argu, (*p. Loc)->data. Ptr)) ) #define COMPARE_LAST ((* p. List->compare) (p. Argu, p. List->rear->data. Ptr)) int result; *p. Pre = NULL; *p. Loc = p. List->head; if (p. List->count == 0) return false; } if ( COMPARE_LAST > 0) { *p. Pre = p. List->rear; *p. Loc = NULL; return false; } while ( (result = COMPARE) > 0 ) { *p. Pre = *p. Loc; *p. Loc = (*p. Loc)->link; } if (result == 0) return true; else return false; [TABLE 5 -1] Target>Last p. Pre=Last Node p. Loc=NULL Return is False Data Structure

3. List ADT _search n PP. 249 연습문제 1 w _search 함수 내에서 p. Head = p. Head->link 와 같은 코딩을 사용하면 어떨까? w 왜 p. Pre와 p. Loc을 별도로 사용할까? 23 Data Structure

3. List ADT _insert n Given the predecessor, there are three steps to the insertion w 1. Allocate memory for the new node and move data to the node w 2. Point the new node to its successor w 3. Point the new node’s predecessor to the new node. n Cases of Predecessor point w Case I) NULL (_search 결과 *p. Pre 가 NULL 인 경우, Case (b) - 1 ) n 1. The new node is inserted to the beginning of the list, or n 2. List is empty w Case II) contain the address of a node (_search 결과 *p. Pre 가 NULL 이 아 닌 경우, Case (b) – 2, 3 ) 24 n 1. The new node is inserted in the middle of the list, or n 2. The new node is inserted at the end of the list Data Structure
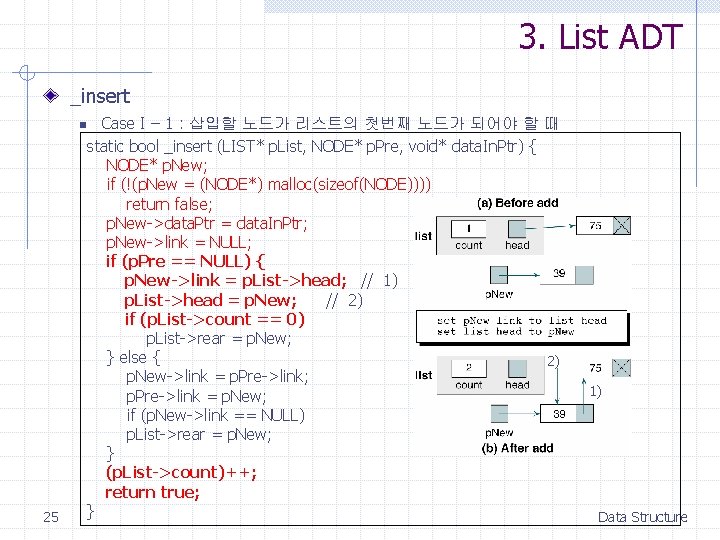
3. List ADT _insert n 25 Case I – 1 : 삽입할 노드가 리스트의 첫번째 노드가 되어야 할 때 static bool _insert (LIST* p. List, NODE* p. Pre, void* data. In. Ptr) { NODE* p. New; if (!(p. New = (NODE*) malloc(sizeof(NODE)))) return false; p. New->data. Ptr = data. In. Ptr; p. New->link = NULL; if (p. Pre == NULL) { p. New->link = p. List->head; // 1) p. List->head = p. New; // 2) if (p. List->count == 0) p. List->rear = p. New; } else { 2) p. New->link = p. Pre->link; p. Pre->link = p. New; if (p. New->link == NULL) p. List->rear = p. New; } (p. List->count)++; return true; } 1) Data Structure
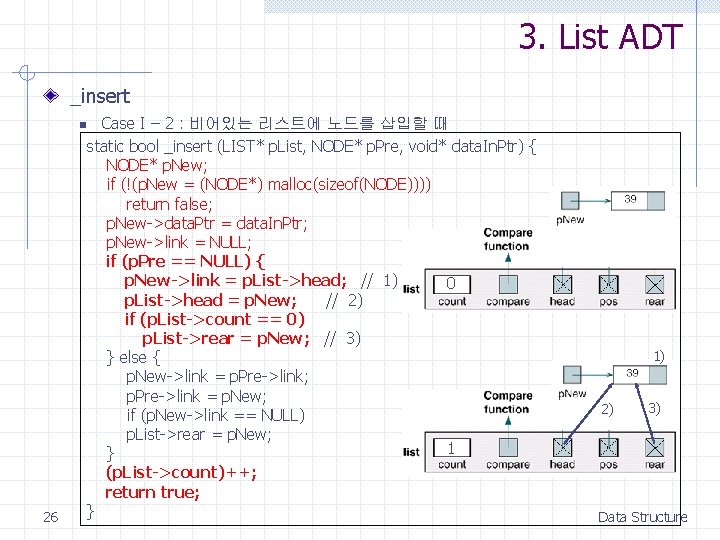
3. List ADT _insert n 26 Case I – 2 : 비어있는 리스트에 노드를 삽입할 때 static bool _insert (LIST* p. List, NODE* p. Pre, void* data. In. Ptr) { NODE* p. New; if (!(p. New = (NODE*) malloc(sizeof(NODE)))) return false; p. New->data. Ptr = data. In. Ptr; p. New->link = NULL; if (p. Pre == NULL) { p. New->link = p. List->head; // 1) 0 p. List->head = p. New; // 2) if (p. List->count == 0) p. List->rear = p. New; // 3) } else { p. New->link = p. Pre->link; p. Pre->link = p. New; if (p. New->link == NULL) p. List->rear = p. New; 1 } (p. List->count)++; return true; } 1) 2) 3) Data Structure

3. List ADT _insert n 27 Case II – 1 : 삽입할 노드가 리스트 중간에 위치 static bool _insert (LIST* p. List, NODE* p. Pre, void* data. In. Ptr) { NODE* p. New; if (!(p. New = (NODE*) malloc(sizeof(NODE)))) return false; p. New->data. Ptr = data. In. Ptr; p. New->link = NULL; if (p. Pre == NULL) { p. New->link = p. List->head; p. List->head = p. New; if (p. List->count == 0) p. List->rear = p. New; } else { p. New->link = p. Pre->link; // 1) p. Pre->link = p. New; // 2) if (p. New->link == NULL) p. List->rear = p. New; } (p. List->count)++; return true; } 2) 1) Data Structure
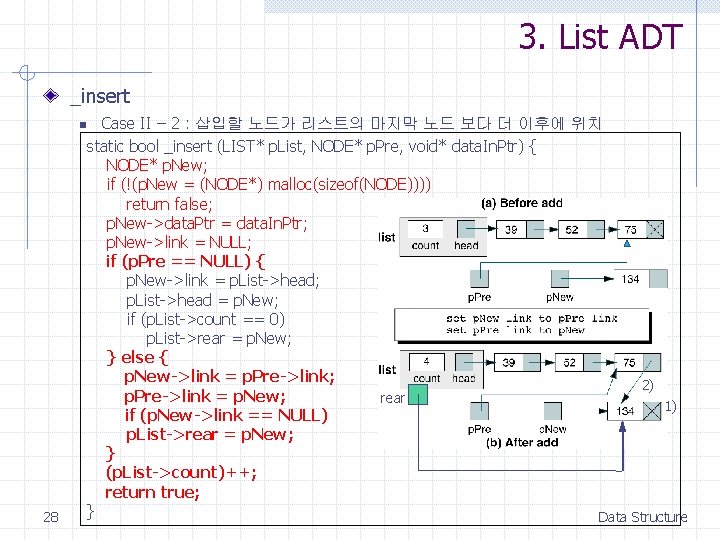
3. List ADT _insert n 28 Case II – 2 : 삽입할 노드가 리스트의 마지막 노드 보다 더 이후에 위치 static bool _insert (LIST* p. List, NODE* p. Pre, void* data. In. Ptr) { NODE* p. New; if (!(p. New = (NODE*) malloc(sizeof(NODE)))) return false; p. New->data. Ptr = data. In. Ptr; p. New->link = NULL; if (p. Pre == NULL) { p. New->link = p. List->head; p. List->head = p. New; if (p. List->count == 0) p. List->rear = p. New; } else { p. New->link = p. Pre->link; 2) p. Pre->link = p. New; rear 1) if (p. New->link == NULL) p. List->rear = p. New; } (p. List->count)++; return true; } Data Structure

3. List ADT remove. Node n p. Pre: _search() 호출 결과 삭제하고자 하는 노드의 바로 이전 노드의 포인터 n p. Loc: _search() 호출 결과 삭제하고자 하는 노드의 포인터 bool remove. Node (LIST* p. List, void* key. Ptr, void** data. Out. Ptr) { bool found; 삭제하고자 하는 NODE* p. Pre; 노드의 데이터값 NODE* p. Loc; found = _search(p. List, &p. Pre, &p. Loc, key. Ptr); if (found) _delete(p. List, p. Pre, p. Loc, data. Out. Ptr); } 29 return found; _delete() 이후에 삭제된 노드의 데이터 값이 할당됨 Data Structure
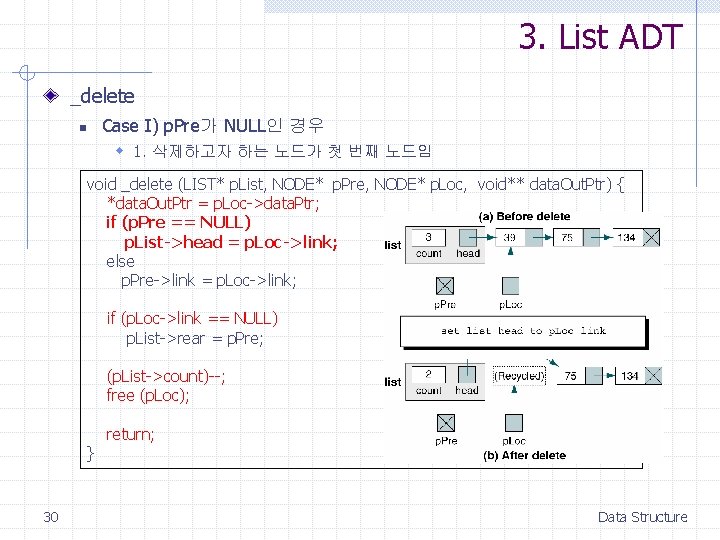
3. List ADT _delete n Case I) p. Pre가 NULL인 경우 w 1. 삭제하고자 하는 노드가 첫 번째 노드임 void _delete (LIST* p. List, NODE* p. Pre, NODE* p. Loc, void** data. Out. Ptr) { *data. Out. Ptr = p. Loc->data. Ptr; if (p. Pre == NULL) p. List->head = p. Loc->link; else p. Pre->link = p. Loc->link; if (p. Loc->link == NULL) p. List->rear = p. Pre; (p. List->count)--; free (p. Loc); } 30 return; Data Structure
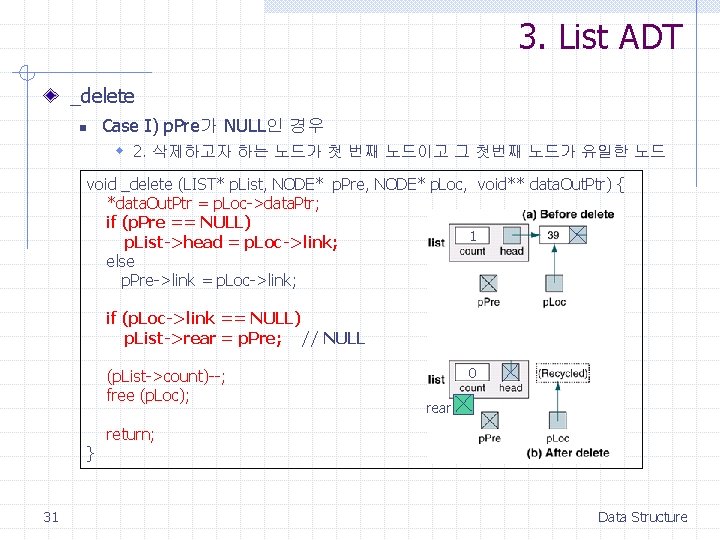
3. List ADT _delete n Case I) p. Pre가 NULL인 경우 w 2. 삭제하고자 하는 노드가 첫 번째 노드이고 그 첫번째 노드가 유일한 노드 void _delete (LIST* p. List, NODE* p. Pre, NODE* p. Loc, void** data. Out. Ptr) { *data. Out. Ptr = p. Loc->data. Ptr; if (p. Pre == NULL) 1 p. List->head = p. Loc->link; else p. Pre->link = p. Loc->link; if (p. Loc->link == NULL) p. List->rear = p. Pre; // NULL (p. List->count)--; free (p. Loc); } 31 0 rear return; Data Structure
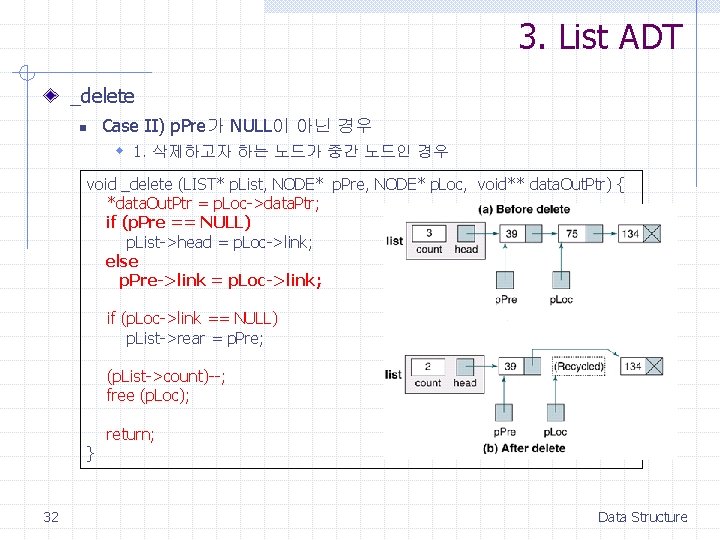
3. List ADT _delete n Case II) p. Pre가 NULL이 아닌 경우 w 1. 삭제하고자 하는 노드가 중간 노드인 경우 void _delete (LIST* p. List, NODE* p. Pre, NODE* p. Loc, void** data. Out. Ptr) { *data. Out. Ptr = p. Loc->data. Ptr; if (p. Pre == NULL) p. List->head = p. Loc->link; else p. Pre->link = p. Loc->link; if (p. Loc->link == NULL) p. List->rear = p. Pre; (p. List->count)--; free (p. Loc); } 32 return; Data Structure
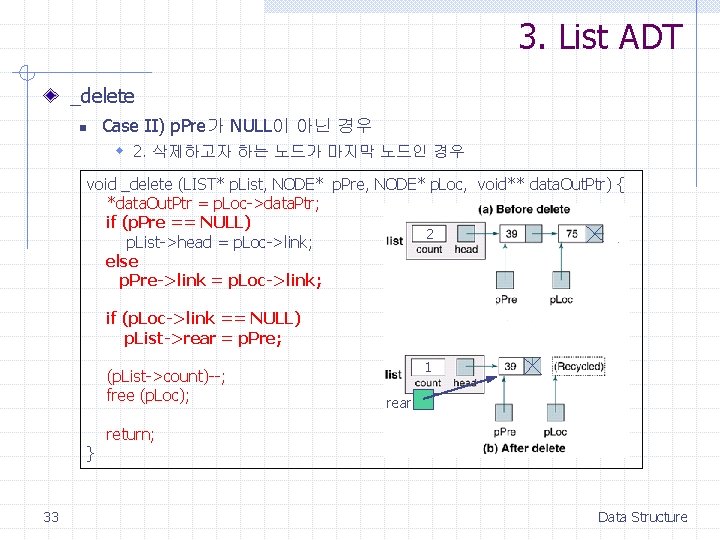
3. List ADT _delete n Case II) p. Pre가 NULL이 아닌 경우 w 2. 삭제하고자 하는 노드가 마지막 노드인 경우 void _delete (LIST* p. List, NODE* p. Pre, NODE* p. Loc, void** data. Out. Ptr) { *data. Out. Ptr = p. Loc->data. Ptr; if (p. Pre == NULL) 2 p. List->head = p. Loc->link; else p. Pre->link = p. Loc->link; if (p. Loc->link == NULL) p. List->rear = p. Pre; (p. List->count)--; free (p. Loc); } 33 1 rear return; Data Structure

3. List ADT search. List bool search. List (LIST* p. List, void* p. Argu, void** p. Data. Out) { bool found; NODE* p. Pre; NODE* p. Loc; } 34 검색하고자 하는 노드의 데이터값 found = _search (p. List, &p. Pre, &p. Loc, p. Argu); if (found) *p. Data. Out = p. Loc->data. Ptr; else *p. Data. Out = NULL; return found; _search() 이후에 검색된 노드의 데이터 값이 할당됨 Data Structure

3. List ADT retrieve. Node static bool retrieve. Node (LIST* p. List, void* p. Argu, void** data. Out. Ptr) { bool found; NODE* p. Pre; NODE* p. Loc; 검색하고자 하는 노드의 데이터값 found = _search (p. List, &p. Pre, &p. Loc, p. Argu); if (found) { *data. Out. Ptr = p. Loc->data. Ptr; return true; } } 35 *data. Out. Ptr = NULL; return false; _search() 이후에 검색된 노드의 데이터 값이 할당됨 n 앞의 search. List와 그 기능이 동일함 n 함수 선언 앞에 static이 있어서 내부 함수로서만 사용할 목적을 지님 Data Structure

3. List ADT empty. List bool empty. List (LIST* p. List) { return (p. List->count == 0); } full. List bool full. List (LIST* p. List) { NODE* temp; if ((temp = (NODE*)malloc(sizeof(*(p. List->head))))) { free (temp); return false; } return true; } list. Count int list. Count(LIST* p. List) { return p. List->count; } 36 Data Structure

3. List ADT traverse. List from. Where: 0 to start at the first element n bool traverse (LIST* p. List, int from. Where, void** data. Ptr. Out) { if (p. List->count == 0) return false; } 37 if (from. Where == 0) { p. List->pos = p. List->head; *data. Ptr. Out = p. List->pos->data. Ptr; return true; } else { if (p. List->pos->link == NULL) return false; else { p. List->pos = p. List->pos->link; *data. Ptr. Out = p. List->pos->data. Ptr; return true; } } traverse() 함수는 한번 불리워질 때마다 현재 리턴하는 값을 지닌 노드 포인터를 p. List->pos에 저장을 해 둔다. 그래서, 다음 번 traverse()를 부를 때에는 이미 p. List->pos는 바로 직전에 리턴받은 노드의 포인터를 가지고 있다. 즉, traverse() 함수는 main()에서 for나 wile 루프 속에서 사용하여 전체 노드의 값들을 가져올 때 유용하게 사용할 수 있다. Data Structure

3. List ADT traverse. List n int traverse. List(List *p. List, int from. Where, void** data. Ptr. Out); w p. List: an ordered list w from. Where: if from. Where == 0 n p. List->pos = p. List->head (pos 포인터의 초기화) n return first data w data. Ptr. Out: an address to receive the next data w Return value: TRUE if next node exists, otherwise, FALSE n Usecase) Printing all data using traverse. List operation int n = 0; int* data; bool ret; // current index do { ret = traverse. List(p. List, n++, (void**)&data); if(ret) printf("%d ", *data); } while(ret); 38 Data Structure

3. List ADT destroy. List LIST* destroy. List (LIST* p. List) { NODE* delete. Ptr; if (p. List) { while (p. List->count > 0) { free (p. List->head->data. Ptr); delete. Ptr = p. List->head; p. List->head = p. List->head->link; p. List->count--; free (delete. Ptr); } free (p. List); } 39 } return NULL; Data Structure
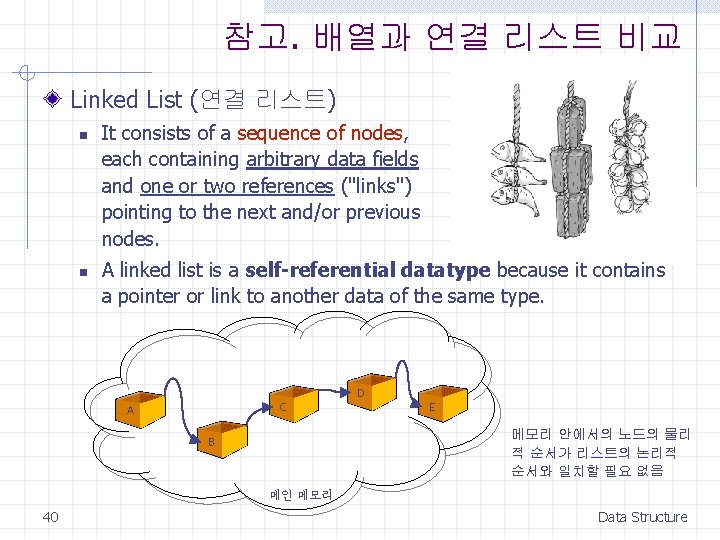
참고. 배열과 연결 리스트 비교 Linked List (연결 리스트) n n It consists of a sequence of nodes, each containing arbitrary data fields and one or two references ("links") pointing to the next and/or previous nodes. A linked list is a self-referential datatype because it contains a pointer or link to another data of the same type. D C A E 메모리 안에서의 노드의 물리 적 순서가 리스트의 논리적 순서와 일치할 필요 없음 B 메인 메모리 40 Data Structure

참고. 배열과 연결 리스트 비교 (General) List n n a list in which operations, such as retrievals, insertions, changes, and deletions, can be done anywhere in the list 일상 생활에서의 예 w Lists of employees w Student lists w Lists of our favorite songs n List의 실제 구현시 선택 방법 w 방법 1) 배열 w 방법 2) 연결 리스트 41 Data Structure

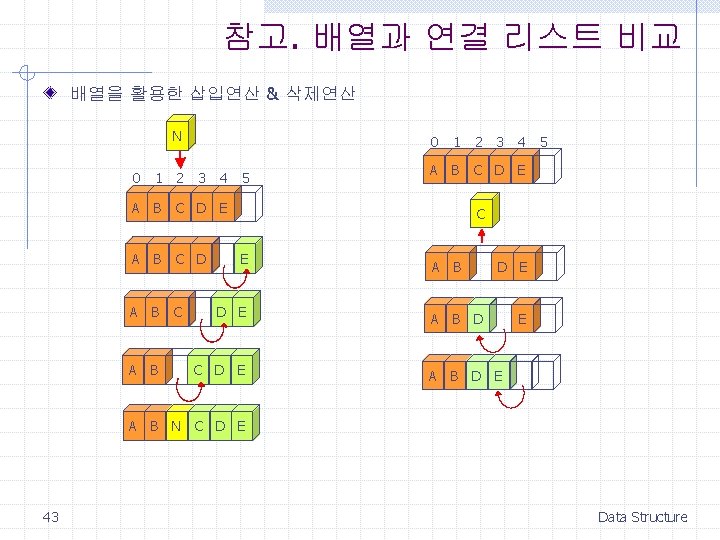

- Slides: 44