Chapter 5 Fundamental Algorithm Design Techniques Overview n

Chapter 5 Fundamental Algorithm Design Techniques

Overview n n n The Greedy Method (5. 1) Divide and Conquer (5. 2) Dynamic Programming (5. 3)

Greedy Outline n n The Greedy Method Technique (§ 5. 1) Fractional Knapsack Problem (§ 5. 1. 1) Task Scheduling (§ 5. 1. 2) Minimum Spanning Trees (§ 7. 3) [future lecture]

A New Vending Machine? n n Coke machine in the lounge behind the ulab—can we hack it? Being efficient computer scientists, we want to return the smallest possible number of coins in change

The Greedy Method

The Greedy Method n The greedy method is a general algorithm design paradigm, built on the following elements: n n n configurations: different choices, collections, or values to find objective function: a score assigned to configurations, which we want to either maximize or minimize It works best when applied to problems with the greedy-choice property: n a globally-optimal solution can always be found by a series of local improvements from a starting configuration.

Making Change n n n Problem: A dollar amount to reach and a collection of coin amounts to use to get there. Configuration: A dollar amount yet to return to a customer plus the coins already returned Objective function: Minimize number of coins returned. Greedy solution: Always return the largest coin you can Example 1: Coins are valued $. 32, $. 08, $. 01 n n Has the greedy-choice property, since no amount over $. 32 can be made with a minimum number of coins by omitting a $. 32 coin (similarly for amounts over $. 08, but under $. 32). Example 2: Coins are valued $. 30, $. 20, $. 05, $. 01 n Does not have greedy-choice property, since $. 40 is best made with two $. 20’s, but the greedy solution will pick three coins (which ones? )

How to rob a bank…

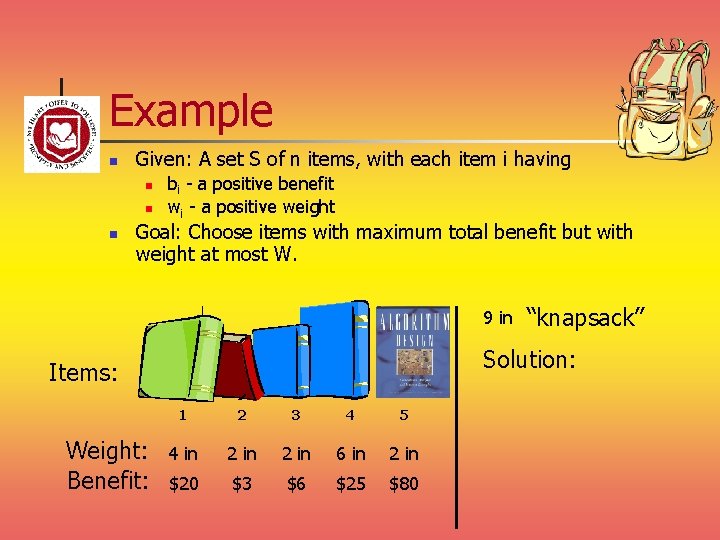
The Fractional Knapsack Problem n Given: A set S of n items, with each item i having n n bi - a positive benefit wi - a positive weight Goal: Choose items with maximum total benefit but with weight at most W. If we are allowed to take fractional amounts, then this is the fractional knapsack problem. n In this case, we let xi denote the amount we take of item i n Objective: maximize n Constraint:

Example n Given: A set S of n items, with each item i having n n n bi - a positive benefit wi - a positive weight Goal: Choose items with maximum total benefit but with weight at most W. “knapsack” Items: Weight: Benefit: Value: ($ per ml) 1 2 3 4 5 4 ml 8 ml 2 ml 6 ml 1 ml $12 $32 $40 $30 $50 3 4 20 5 50 Solution: • 1 ml of 5 • 2 ml of 3 • 6 ml of 4 • 1 ml of 2 10 ml

The Fractional Knapsack Algorithm n Greedy choice: Keep taking item with highest value (benefit to weight ratio) n n n Since Run time: O(n log n). Why? Correctness: Suppose there is a better solution n n there is an item i with higher value than a chosen item j, but xi<wi, xj>0 and vi<vj If we substitute some i with j, we get a better solution How much of i: min{wi-xi, xj} Thus, there is no better solution than the greedy one Algorithm fractional. Knapsack(S, W) Input: set S of items w/ benefit bi and weight wi; max. weight W Output: amount xi of each item i to maximize benefit w/ weight at most W for each item i in S xi 0 vi bi / wi {value} w 0 {total weight} while w < W remove item i w/ highest vi xi min{wi , W - w} w w + min{wi , W - w}

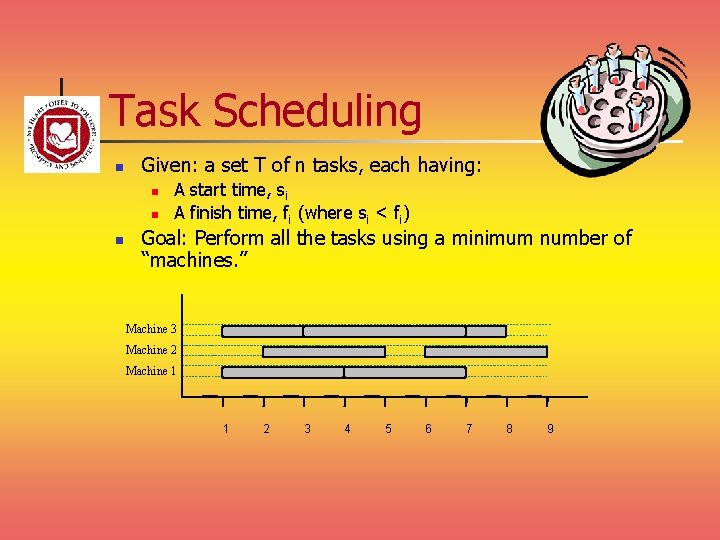
Task Scheduling n Given: a set T of n tasks, each having: n n n A start time, si A finish time, fi (where si < fi) Goal: Perform all the tasks using a minimum number of “machines. ” Machine 3 Machine 2 Machine 1 1 2 3 4 5 6 7 8 9

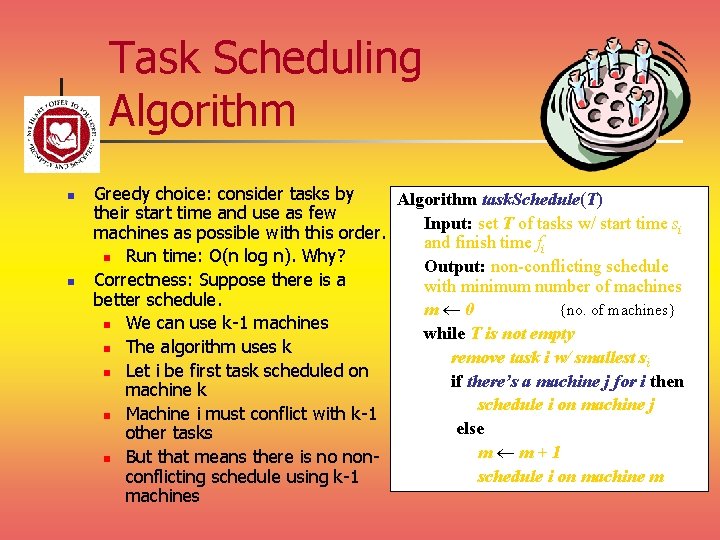
Task Scheduling Algorithm n n Greedy choice: consider tasks by Algorithm task. Schedule(T) their start time and use as few Input: set T of tasks w/ start time si machines as possible with this order. and finish time fi n Run time: O(n log n). Why? Output: non-conflicting schedule Correctness: Suppose there is a with minimum number of machines better schedule. m 0 {no. of machines} n We can use k-1 machines while T is not empty n The algorithm uses k remove task i w/ smallest si n Let i be first task scheduled on if there’s a machine j for i then machine k schedule i on machine j n Machine i must conflict with k-1 else other tasks m m+1 n But that means there is no nonschedule i on machine m conflicting schedule using k-1 machines

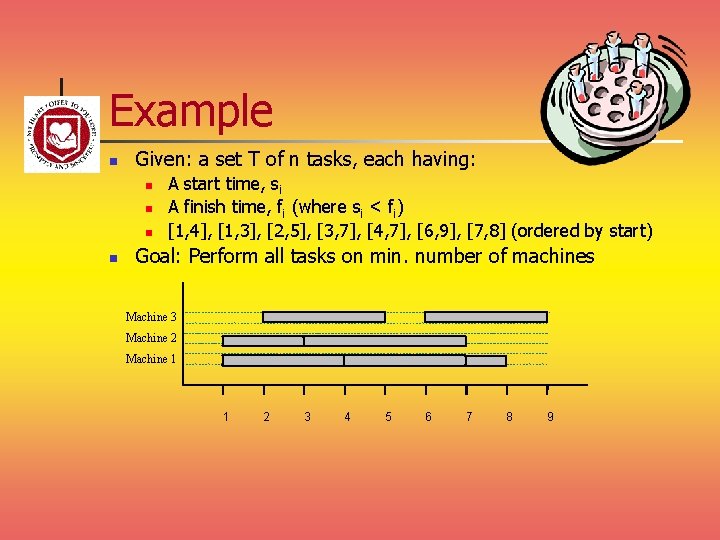
Example n Given: a set T of n tasks, each having: n n A start time, si A finish time, fi (where si < fi) [1, 4], [1, 3], [2, 5], [3, 7], [4, 7], [6, 9], [7, 8] (ordered by start) Goal: Perform all tasks on min. number of machines Machine 3 Machine 2 Machine 1 1 2 3 4 5 6 7 8 9

Divide-and-Conquer 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 9 4 4 9 9 9 4 4

Outline and Reading n n n Divide-and-conquer paradigm (§ 5. 2) Review Merge-sort (§ 4. 1. 1) Recurrence Equations (§ 5. 2. 1) n n n Iterative substitution Recursion trees Guess-and-test The master method Integer Multiplication (§ 5. 2. 2)

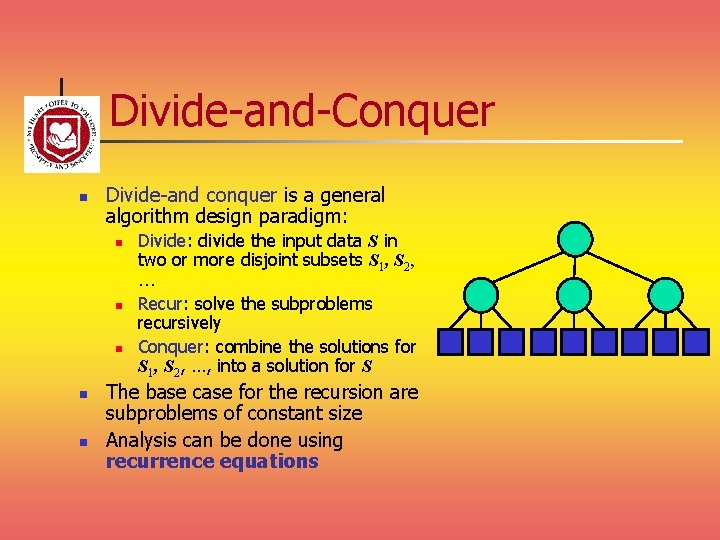
Divide-and-Conquer n Divide-and conquer is a general algorithm design paradigm: n n n Divide: divide the input data S in two or more disjoint subsets S 1, S 2, … Recur: solve the subproblems recursively Conquer: combine the solutions for S 1, S 2, …, into a solution for S The base case for the recursion are subproblems of constant size Analysis can be done using recurrence equations

Binary Search n n n I have a number X between c 1 and c 2… Divide and conquer algorithm? Analysis: n n Called a Recurrence Equation How to solve?

Solving the Binary Search Recurrence T(n) = T(n/2) + c T(n/2) = T(n/4) + c T(n/4) = T(n/8) + c … -----T(n) = T(n/2) + c = [T(n/4) + c] + c = T(n/22) + 2 c = T(n/23) + 3 c [telescope] = T(n/2 k) + k c done when k=lg n; then T(n/2 k)=T(1) is base case = b + c lg n

Merge Sort Recurrence Equation Analysis n n n Recurrence Equation? We can analyze by finding a closed form solution. Method: expand telescope

Solving the Merge Sort recurrence T(n) = 2 T(n/2) + b n T(n/2) = 2 T(n/4) + b n/2 T(n/4) = 2 T(n/8) + b n/4 … -----T(n) = 2 T(n/2) + b n = 2[2 T(n/4) + b n/2] + b n = 22 T(n/22) + 2 b n = 23 T(n/23) + 3 b n [telescope] = 2 k. T(n/2 k) + k b n done when k=lg n; then T(n/2 k)=T(1) is base case = b n + b n lg n

Min & Max n n n Given a set of n items, find the min and max. How many comparisons needed? Simple alg: n-1 comparisons to find min, n-1 for max Recursive algorithm: void minmax(int i, int j, int& min 0, int& max 0) { if (j<=i+1) [handle base case; return] m=(i+j+1)/2; minmax(i, m-1, min 1, max 1); minmax(m, j, min 2, max 2); min 0 = min(min 1, min 2); max 0 = max(max 1, max 2); } Recurrence: T(n)=2 T(n/2) + 2; T(2)=1 Solution? 1. 5 n - 2

Solving the Min&Max Recurrence T(n) = 2 T(n/2) + 2; T(2)=1 T(n/2) = 2 T(n/4) + 2 T(n/4) = 2 T(n/8) + 2 … -----T(n) = 2 T(n/2) + 2 = 2[2 T(n/4) + 2] + 2 = 22 T(n/22) + 22 + 2 = 23 T(n/23) + 23 + 22 + 2 [telescope] = 2 k. T(n/2 k) + 2 k+1 - 2 done when k=(lg n) - 1; then T(n/2 k)=T(2) is base case = n/2 + n – 2 = 1. 5 n - 2

Hanoi runtime? void hanoi(n, from, to, spare { if (n > 0) { hanoi(n-1, from, spare, to); cout << from << “ – “ << to << endl; hanoi(n-1, spare, to, from); } } T(n) = 2 T(n-1) + c T(0) = b Look it up: T(n) = O(2 n)

Master Method Another way to solve recurrences: “Look it up” n The Master Theorem solves many of them: If T(n)=c, n<d, and T(n)=a. T(n/b)+f(n), n≥d, and for small constants e>0, k>=0, and d<1 then n n If f(n) is O( ) then T(n) is Q( ) n If f(n) is Q( ) then T(n) is Q( ) n If f(n) is W( ) and a f(n/b) ≤ df(n), for n ≤ d, then T(n) is Q(f(n))

An Important use of Recurrence Relations by Donald Knuth

09 -0804

More Divide and Conquer Examples n n pow(x, n) log(n, base) Point-in-convex-polygon Fractals

09 -0804

09 -0804

n http: //www. 3 villagecsd. k 12. ny. us/wmhs/Departments/Math/OBrien/fibonacci 2. html

n http: //www. religiousforums. com/forum/material-world/80450 -fibonacci-sequence. html

Creating Fractals n n Koch Snowflake Fractal Star Sierpinski Gasket Your own…

Practice Analyzing Recursive Functions 1. int fun 1(int n) { if (n==1) return 50; return fun 1(n/2) * fun 1(n/2) + 97; } 2. int fun 2(int n) { if (n==1) return 1; int sum=0; for (int i=1; i<=n; i++) sum += fun 2(n-1); return sum; }

Dynamic Programming

Outline and Reading n n n Fibonacci Making Change Matrix Chain-Product (§ 5. 3. 1) The General Technique (§ 5. 3. 2) 0 -1 Knapsack Problem (§ 5. 3. 3)

Opinions? public class Fib { public static Big. Integer fibonacci(long n) { if (n <= 2) return new Big. Integer("1"); return fibonacci(n-1). add(fibonacci(n-2)); } public static void main( String args[] ) { long n = Integer. parse. Int(args[0]); System. out. println("Fib(" + n + ") = " + fibonacci(n). to. String()); } }

Bottom up… public class Fib 2 { static Big. Integer[] fibs; public static Big. Integer fibonacci(int n) { Big. Integer result; fibs[1]=new Big. Integer("1"); fibs[2]=new Big. Integer("1"); for (int i=3; i<=n; i++) fibs[i] = fibs[i-1]. add(fibs[i-2]); return fibs[n]; } public static void main( String args[] ) { int n = Integer. parse. Int(args[0]); fibs = new Big. Integer[n+1]; System. out. println("Fib(" + n + ") = " + fibonacci(n). to. String()); } }

Memoize… public class Fib 3 { static Big. Integer[] fibs; public static Big. Integer fibonacci(int n) { long result; if (fibs[n] != null) return fibs[n]; else { fibs[n] = fibonacci(n-1). add(fibonacci(n-2)); return fibs[n]; } } public static void main( String args[] ) { int n = Integer. parse. Int(args[0]); fibs = new Big. Integer [n+1]; fibs[1] = new Big. Integer("1"); fibs[2] = new Big. Integer("1"); System. out. println("Fib("+n+") = " + fibonacci(n)); } }

Dynamic Programming n n n Applies to problems that can be solved recursively, but the subproblems overlap (Typically optimization problems) Method: n n n Write definition of value you want to compute Express solution in terms of sub-problem solutions Compute bottom-up or “memoize”

Making Change n n Being good Computer Scientists, we want to have a General Solution for making change in our vending machine. Suppose that our coin values were 40, 30, 5, and 1 cent? How would we make change using the smallest number of coins?

Making Change – DP solution n Suppose we have coin values c 1, c 2, …, ck and we want to make change for value V using the smallest number of coins? What sub-problem solutions would give us solution to the whole problem? Define NC(V) = smallest number of coins that will add up to V. n n Base case? Run time? n n Some kind of exponential, if you’re not careful… How can we implement this efficiently?

Dynamic Programming: Two methods for efficiency n Build a table bottom-up n n Compute NC(1), NC(2), …, NC(V), storing subproblem results in a table as you go up Memoize n Compute NC(V) recursively, but store new subproblem results when you first compute them

Making change example n Suppose coin values are 1, 5, 7 and v=10 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 ∞ ∞ ∞ 0 1 2 3 4 1 2 3 10 11 12 13

Making change example Suppose coin values are 1, 5, 7 and v=10 n -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 ∞ ∞ ∞ 0 1 2 3 4 1 2 3 n n 10 11 12 13 NC[10] = 1 + Min (NC[9], NC[5], NC[3]) Runtime?

Forgot your hacksaw?

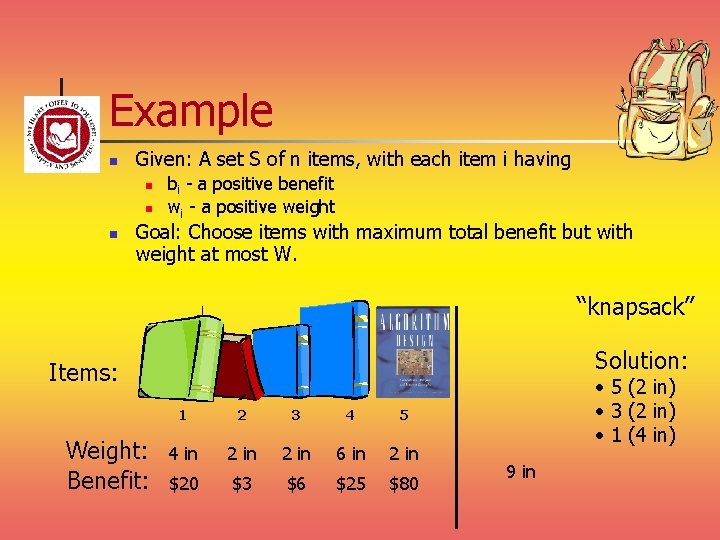
The 0/1 Knapsack Problem n Given: A set S of n items, with each item i having n n bi - a positive benefit wi - a positive weight Goal: Choose items with maximum total benefit but with weight at most W. If we are not allowed to take fractional amounts, then this is the 0/1 knapsack problem. n In this case, we let T denote the set of items we take n Objective: maximize n Constraint:

Example n Given: A set S of n items, with each item i having n n n bi - a positive benefit wi - a positive weight Goal: Choose items with maximum total benefit but with weight at most W. 9 in Solution: Items: Weight: Benefit: “knapsack” 1 2 3 4 5 4 in 2 in 6 in 2 in $20 $3 $6 $25 $80

Example n Given: A set S of n items, with each item i having n n n bi - a positive benefit wi - a positive weight Goal: Choose items with maximum total benefit but with weight at most W. “knapsack” Solution: Items: Weight: Benefit: 1 2 3 4 5 4 in 2 in 6 in 2 in $20 $3 $6 $25 $80 • 5 (2 in) • 3 (2 in) • 1 (4 in) 9 in

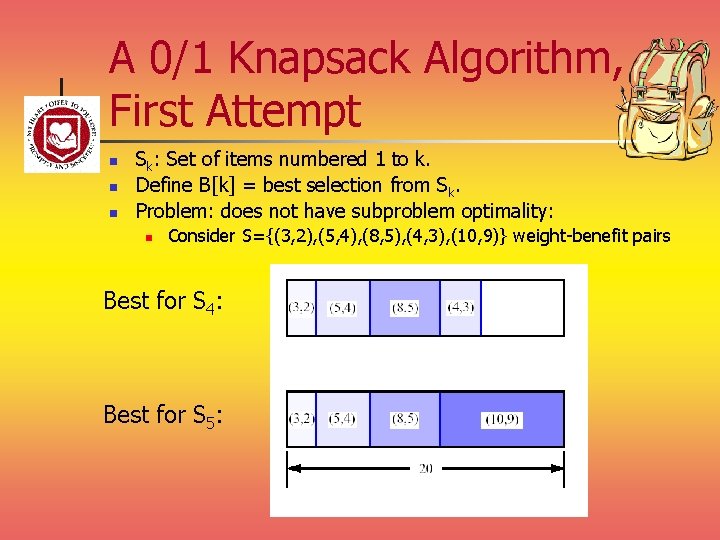
A 0/1 Knapsack Algorithm, First Attempt n n n Sk: Set of items numbered 1 to k. Define B[k] = best selection from Sk. Problem: does not have subproblem optimality: n Consider S={(3, 2), (5, 4), (8, 5), (4, 3), (10, 9)} weight-benefit pairs Best for S 4: Best for S 5:

A 0/1 Knapsack Algorithm, Second Attempt n

(Weight, Value): (4, 7) (3, 4) (8, 17) (6, 14) (5, 10) (7, 16) B 1 2 3 4 5 6 7 8 9 10 11 12 13 14 S 1 0 0 0 7 7 7 S 2 0 0 4 7 7 7 11 11 S 3 0 0 4 7 7 7 11 17 17 17 21 28 28 28 S 4 0 0 4 7 14 14 14 17 18 21 21 S 5 S 6 Runtime? How to tell which objects were used for each box?

(Weight, Value): (4, 7) (3, 4) (8, 17) (6, 14) (5, 10) (7, 16) B 1 2 3 4 5 6 7 8 9 10 11 12 13 14 S 1 0 0 0 7 7 7 S 2 0 0 4 7 7 7 11 11 S 3 0 0 4 7 7 7 11 17 17 17 21 28 28 28 S 4 0 0 4 7 14 14 14 17 18 21 21 28 28 31 S 5 0 0 4 7 14 14 14 17 18 24 24 28 28 31 S 6 0 0 4 7 14 14 16 16 16 24 24 30 30 31 Runtime? How to tell which objects were used for each box?

The 0/1 Knapsack Algorithm n n n Recall def. of B[k, w]: Since B[k, w] is defined in terms of B[k-1, *], we can reuse the same array Running time: O(n. W). Not a polynomial-time algorithm if W is large This is a pseudo-polynomial time algorithm Algorithm 01 Knapsack(S, W): Input: set S of items w/ benefit bi and weight wi; max. weight W Output: benefit of best subset with weight at most W for w 0 to W do B[w] 0 for k 1 to n do for w W downto wk do if B[w-wk]+bk > B[w] then B[w] B[w-wk]+bk

The General Dynamic Programming Technique n Applies to a problem that at first seems to require a lot of time (possibly exponential), provided we have: n n n Simple subproblems: the subproblems can be defined in terms of a few variables, such as j, k, l, m, and so on. Subproblem optimality: the global optimum value can be defined in terms of optimal subproblems Subproblem overlap: the subproblems are not independent, but instead they overlap (hence, should be constructed bottom -up).

Longest Common Subsequence Given two sequences of tokens, what is the longest pair of (non-contiguous) subsequences? A[1. . n] = A C A G T C A A G A C T B[1. . m] = A G A T C G T A G A T C How to solve? What subproblem solutions would be helpful?

LCS subproblem definition Define subproblem solutions LCS(i, j) = length of the longest common subsequence of A[1. . i], B[1. . j]

LCS solution Define subproblem solutions LCS(i, j) = length of the longest common subsequence of A[1. . i], B[1. . j] LCS(i, j) = 0 if i=0 or j=0. Otherwise: LCS(i, j) = If A[i] != B[j]: max[ LCS(i, j-1), LCS(i-1, j) ] Else: LCS(i-1, j-1) + 1

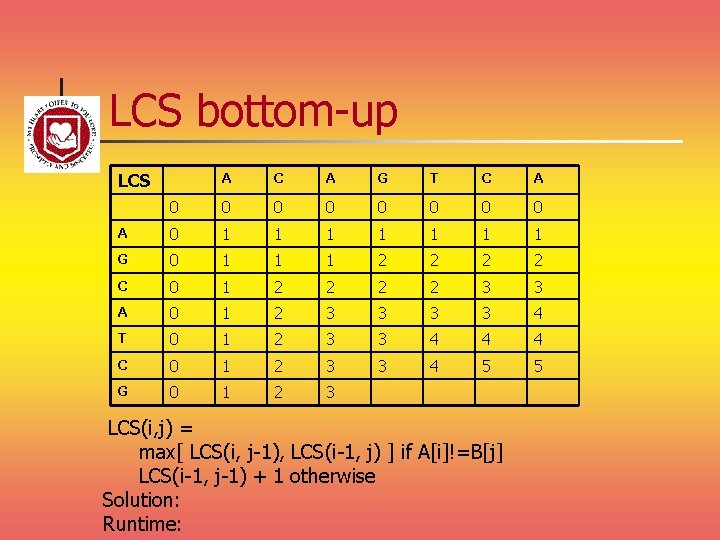
LCS bottom-up LCS A C A G T C A 0 0 0 0 A 0 1 1 1 1 G 0 1 1 1 2 2 C 0 1 2 2 3 3 A 0 1 2 3 3 4 T 0 1 2 3 3 4 4 4 C 0 1 2 3 3 4 5 5 G 0 1 2 3 LCS(i, j) = max[ LCS(i, j-1), LCS(i-1, j) ] if A[i]!=B[j] LCS(i-1, j-1) + 1 otherwise Solution: Runtime:

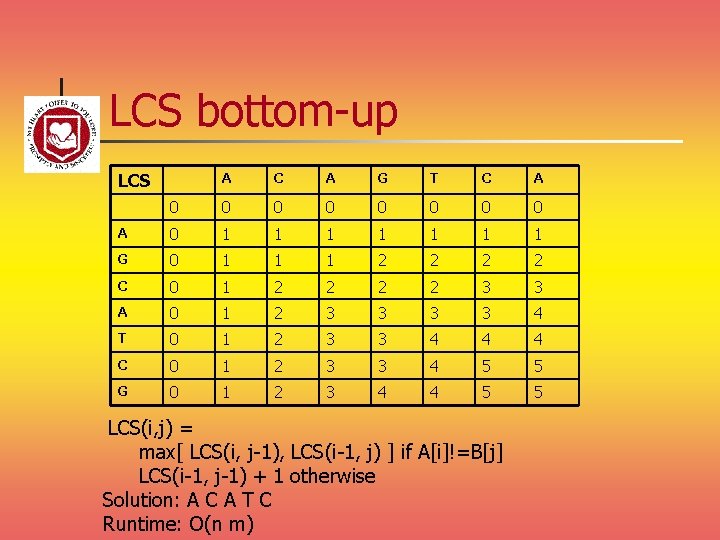
LCS bottom-up LCS A C A G T C A 0 0 0 0 A 0 1 1 1 1 G 0 1 1 1 2 2 C 0 1 2 2 3 3 A 0 1 2 3 3 4 T 0 1 2 3 3 4 4 4 C 0 1 2 3 3 4 5 5 G 0 1 2 3 4 4 5 5 LCS(i, j) = max[ LCS(i, j-1), LCS(i-1, j) ] if A[i]!=B[j] LCS(i-1, j-1) + 1 otherwise Solution: A C A T C Runtime: O(n m)