Chapter 5 Functions II Outline Recursion Examples Using

Chapter 5 – Functions II Outline • Recursion • Examples Using Recursion: The Fibonacci Series

Recursion • Recursive functions – Function that calls itself – Can only solve a base case – Divides up problem into • What it can do • What it cannot do - resembles original problem – Launches a new copy of itself (recursion step) • Eventually base case gets solved – Gets plugged in, works its way up and solves whole problem

Recursion (II) • Example: factorial: 5! = 5 * 4 * 3 * 2 * 1 Notice that 5! = 5 * 4! 4! = 4 * 3!. . . – Can compute factorials recursively – Solve base case (1! = 0! = 1) then plug in • 2! = 2 * 1 = 2; • 3! = 3 * 2 = 6;

Factorial Using Recursion factorial(4) = 4* factorial(3) = 4* 3 * factorial(2) = int factorial(int n){ int result; 4* 3 * 2 * factorial(1) = if (n <= 1) result = 1; 4* 3 * 2 * 1 = else 4* 3 * 2 = 4* 6 = 24 result = n * factorial(n - 1); return result; } W 1 -4

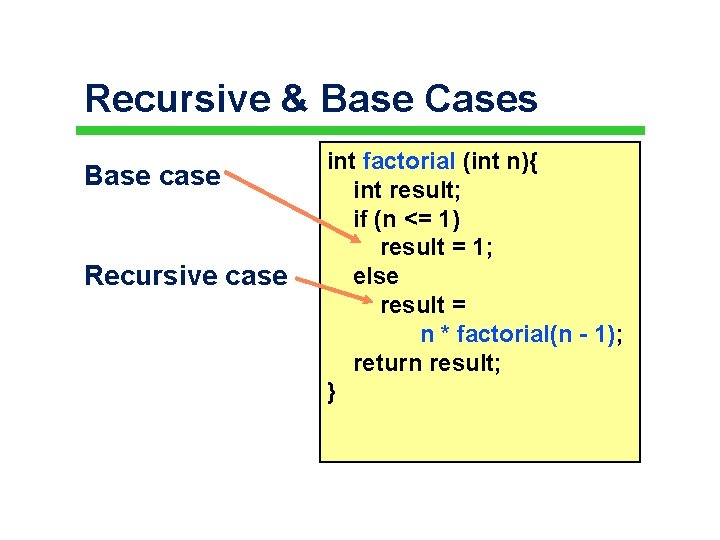
Recursive & Base Cases Base case Recursive case int factorial (int n){ int result; if (n <= 1) result = 1; else result = n * factorial(n - 1); return result; } W 1 -5

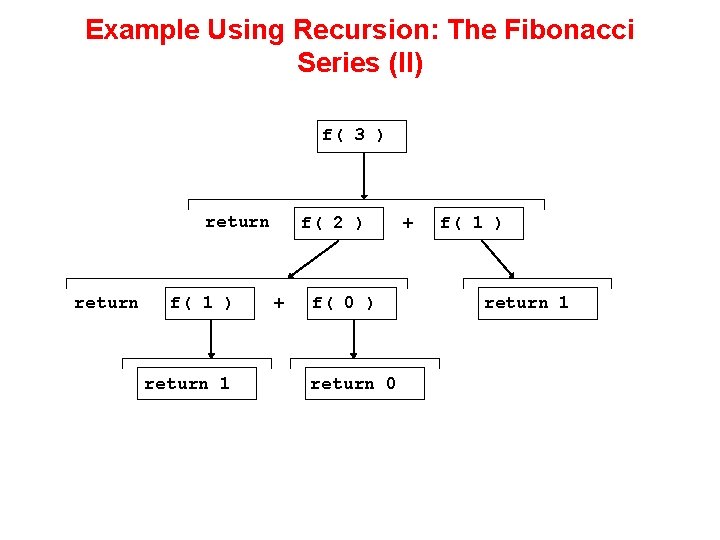
Example Using Recursion: The Fibonacci Series • Fibonacci series: 0, 1, 1, 2, 3, 5, 8. . . – Each number sum of the previous two fib(n) = fib(n-1) + fib(n-2) - recursive formula long fibonacci(long n) { if (n==0 || n==1) //base case return n; else return fibonacci(n-1) + fibonacci(n-2); }

Example Using Recursion: The Fibonacci Series (II) f( 3 ) return f( 1 ) return 1 f( 2 ) + f( 0 ) return 0 + f( 1 ) return 1

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 /* Fig. 5. 15: fig 05_15. c Recursive fibonacci function */ #include <stdio. h> int fibonacci( int ); int main() { int result, number; printf( "Enter an integer: " ); scanf( “%d", &number ); result = fibonacci( number ); printf( "Fibonacci( %d ) = %dn", number, result ); return 0; } /* Recursive definition of function fibonacci */ int fibonacci(int n ) { if ( n == 0 || n == 1 ) return n; else return fibonacci( n - 1 ) + fibonacci( n - 2 ); } Enter an integer: 0 Fibonacci(0) = 0 Enter an integer: 1 Fibonacci(1) = 1 1. Function prototype 1. 1 Initialize variables 2. Input an integer 2. 1 Call function fibonacci 2. 2 Output results. 3. Define fibonacci recursively Program Output

Enter an integer: 2 Fibonacci(2) = 1 Enter an integer: 3 Fibonacci(3) = 2 Enter an integer: 4 Fibonacci(4) = 3 Enter an integer: 5 Fibonacci(5) = 5 Enter an integer: 6 Fibonacci(6) = 8 Enter an integer: 10 Fibonacci(10) = 55 Enter an integer: 20 Fibonacci(20) = 6765 Enter an integer: 30 Fibonacci(30) = 832040 Enter an integer: 35 Fibonacci(35) = 9227465 Program Output

END OF CLASS THANKS EVERYONE!