Chapter 5 Functions Discrete Mathematical Structures Theory and

Chapter 5: Functions Discrete Mathematical Structures: Theory and Applications

Learning Objectives q Learn about functions q Explore various properties of functions q Learn about sequences and strings q Become familiar with the representation of strings in computer memory q Learn about binary operations Discrete Mathematical Structures: Theory and Applications 2

Functions Discrete Mathematical Structures: Theory and Applications 3

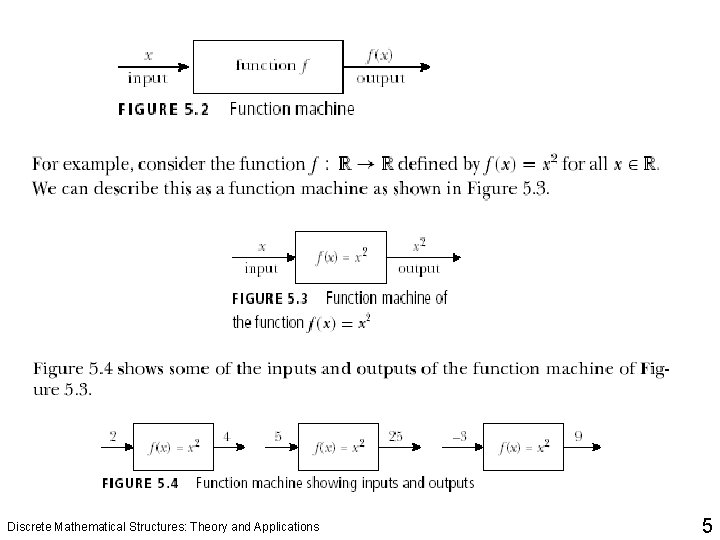
Functions Discrete Mathematical Structures: Theory and Applications 4

Discrete Mathematical Structures: Theory and Applications 5

Discrete Mathematical Structures: Theory and Applications 6

Discrete Mathematical Structures: Theory and Applications 7

Discrete Mathematical Structures: Theory and Applications 8

Discrete Mathematical Structures: Theory and Applications 9

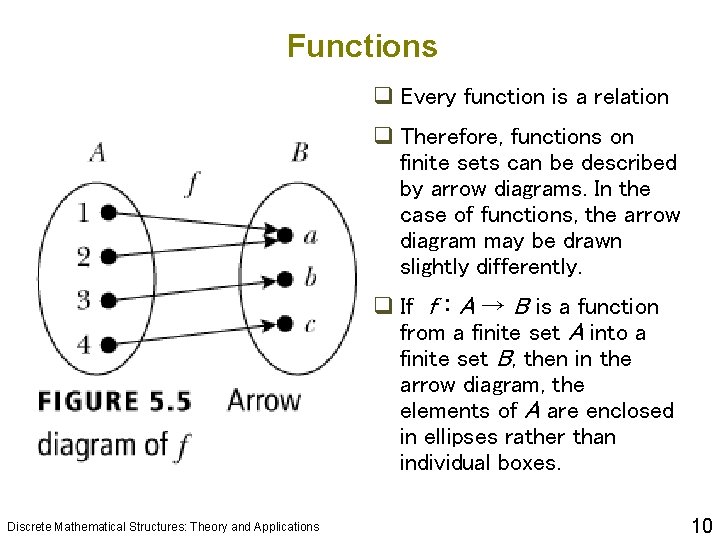
Functions q Every function is a relation q Therefore, functions on finite sets can be described by arrow diagrams. In the case of functions, the arrow diagram may be drawn slightly differently. q If f : A → B is a function from a finite set A into a finite set B, then in the arrow diagram, the elements of A are enclosed in ellipses rather than individual boxes. Discrete Mathematical Structures: Theory and Applications 10

Functions q To determine from its arrow diagram whether a relation f from a set A into a set B is a function, two things are checked: 1) Check to see if there is an arrow from each element of A to an element of B q This would ensure that the domain of f is the set A, i. e. , D(f) = A 2) Check to see that there is only one arrow from each element of A to an element of B q This would ensure that f is well defined Discrete Mathematical Structures: Theory and Applications 11

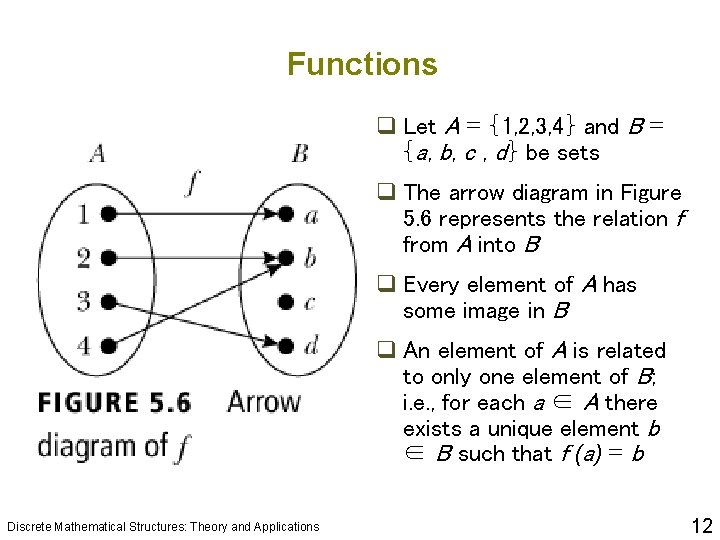
Functions q Let A = {1, 2, 3, 4} and B = {a, b, c , d} be sets q The arrow diagram in Figure 5. 6 represents the relation f from A into B q Every element of A has some image in B q An element of A is related to only one element of B; i. e. , for each a ∈ A there exists a unique element b ∈ B such that f (a) = b Discrete Mathematical Structures: Theory and Applications 12

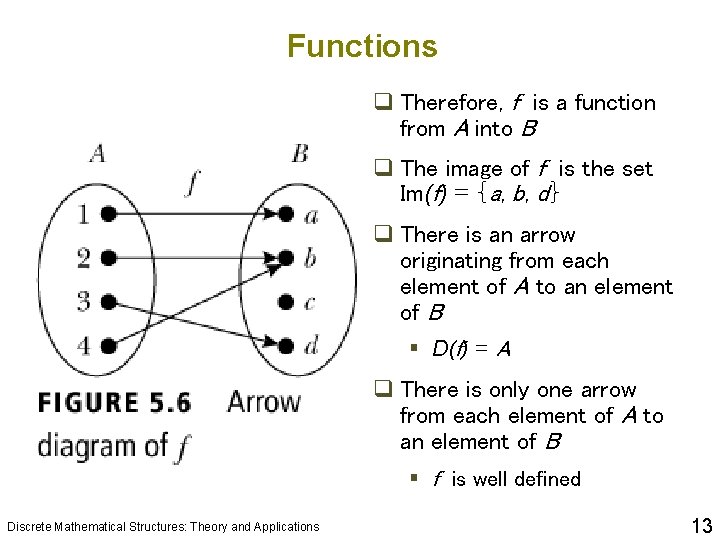
Functions q Therefore, f is a function from A into B q The image of f is the set Im(f) = {a, b, d} q There is an arrow originating from each element of A to an element of B § D(f) = A q There is only one arrow from each element of A to an element of B § f is well defined Discrete Mathematical Structures: Theory and Applications 13

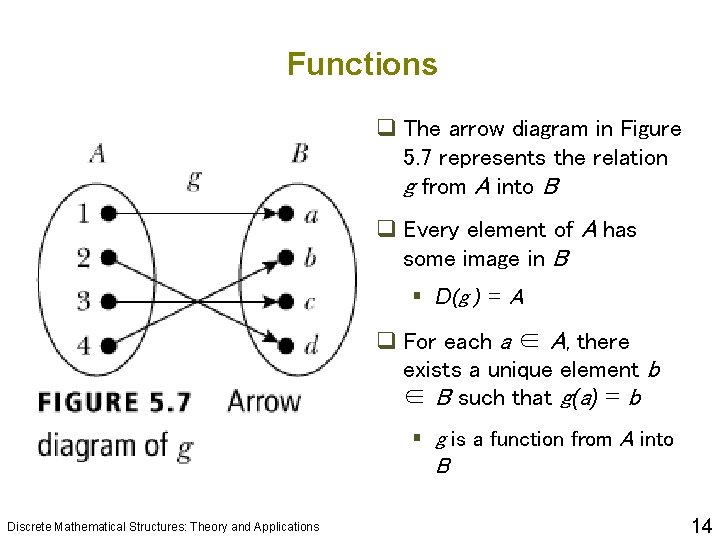
Functions q The arrow diagram in Figure 5. 7 represents the relation g from A into B q Every element of A has some image in B § D(g ) = A q For each a ∈ A, there exists a unique element b ∈ B such that g(a) = b § g is a function from A into B Discrete Mathematical Structures: Theory and Applications 14

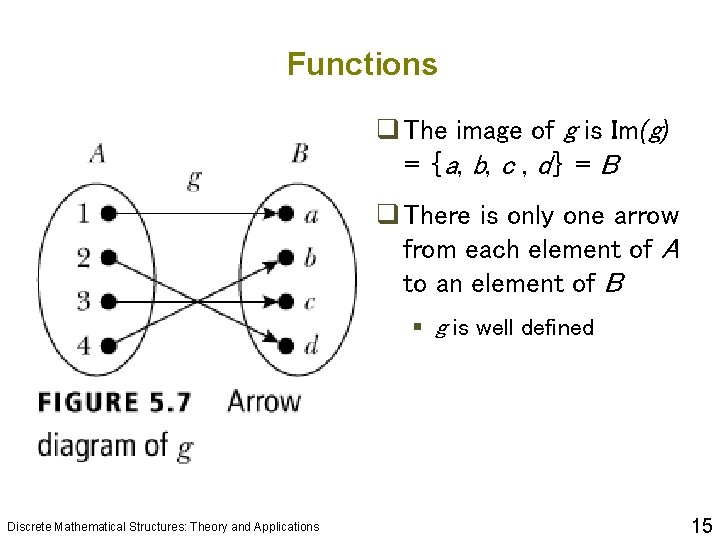
Functions q The image of g is Im(g) = {a , b , c , d } = B q There is only one arrow from each element of A to an element of B § g is well defined Discrete Mathematical Structures: Theory and Applications 15

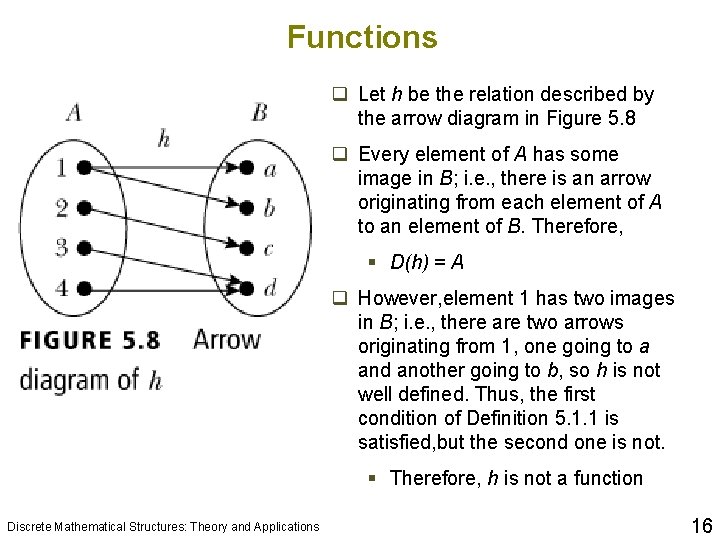
Functions q Let h be the relation described by the arrow diagram in Figure 5. 8 q Every element of A has some image in B; i. e. , there is an arrow originating from each element of A to an element of B. Therefore, § D(h) = A q However, element 1 has two images in B; i. e. , there are two arrows originating from 1, one going to a and another going to b, so h is not well defined. Thus, the first condition of Definition 5. 1. 1 is satisfied, but the second one is not. § Therefore, h is not a function Discrete Mathematical Structures: Theory and Applications 16

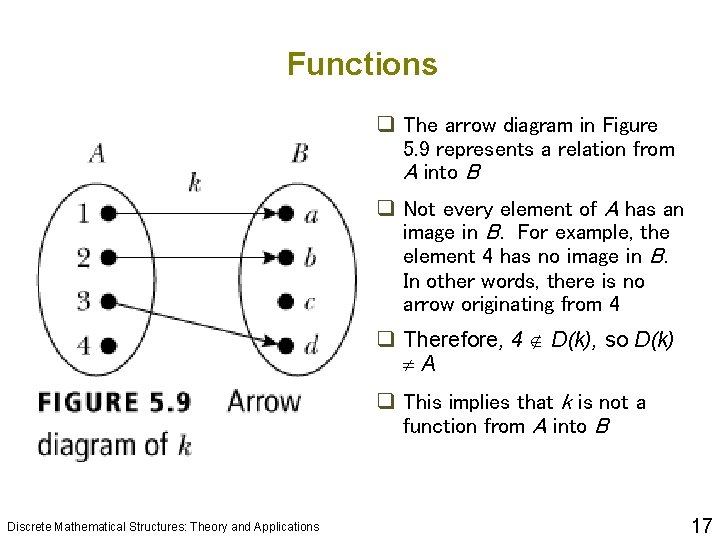
Functions q The arrow diagram in Figure 5. 9 represents a relation from A into B q Not every element of A has an image in B. For example, the element 4 has no image in B. In other words, there is no arrow originating from 4 q Therefore, 4 D(k), so D(k) A q This implies that k is not a function from A into B Discrete Mathematical Structures: Theory and Applications 17

Functions q Numeric Functions § If the domain and the range of a function are numbers, then the function is typically defined by means of an algebraic formula § Such functions are called numeric functions § Numeric functions can also be defined in such a way so that different expressions are used to find the image of an element Discrete Mathematical Structures: Theory and Applications 18

Functions Discrete Mathematical Structures: Theory and Applications 19

Functions Discrete Mathematical Structures: Theory and Applications 20

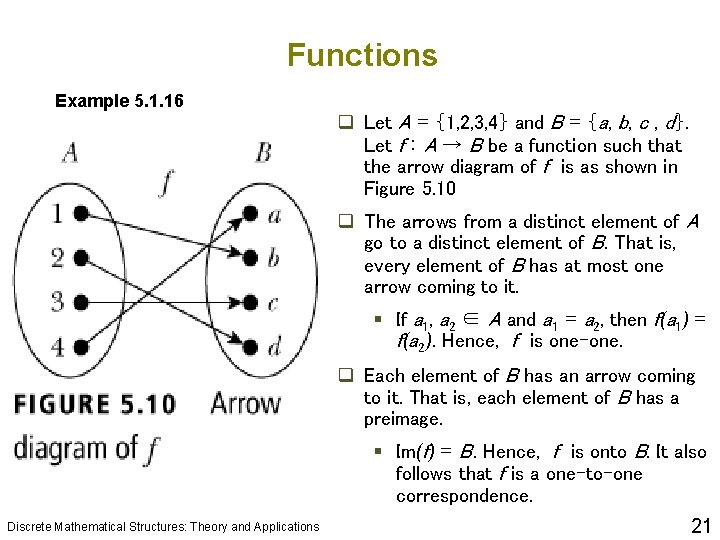
Functions Example 5. 1. 16 q Let A = {1, 2, 3, 4} and B = {a, b, c , d}. Let f : A → B be a function such that the arrow diagram of f is as shown in Figure 5. 10 q The arrows from a distinct element of A go to a distinct element of B. That is, every element of B has at most one arrow coming to it. § If a 1, a 2 ∈ A and a 1 = a 2, then f(a 1) = f(a 2). Hence, f is one-one. q Each element of B has an arrow coming to it. That is, each element of B has a preimage. § Im(f) = B. Hence, f is onto B. It also follows that f is a one-to-one correspondence. Discrete Mathematical Structures: Theory and Applications 21

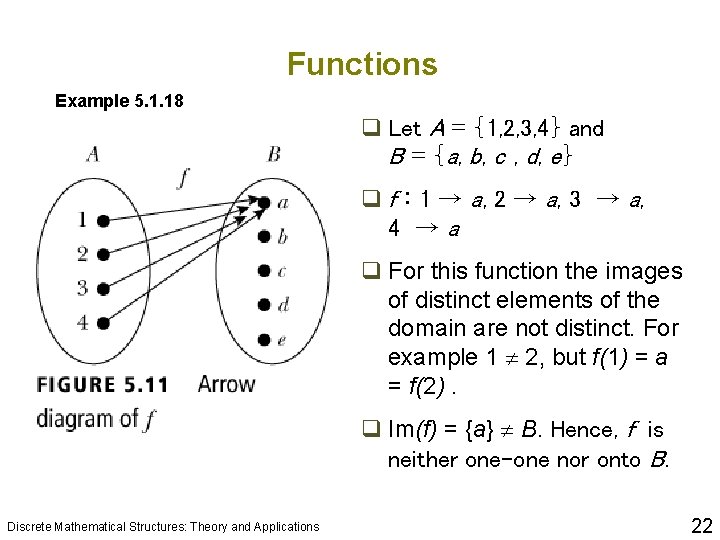
Functions Example 5. 1. 18 q Let A = {1, 2, 3, 4} and B = {a, b, c , d, e} q f : 1 → a, 2 → a, 3 → a, 4 →a q For this function the images of distinct elements of the domain are not distinct. For example 1 2, but f(1) = a = f(2). q Im(f) = {a} B. Hence, f is neither one-one nor onto B. Discrete Mathematical Structures: Theory and Applications 22

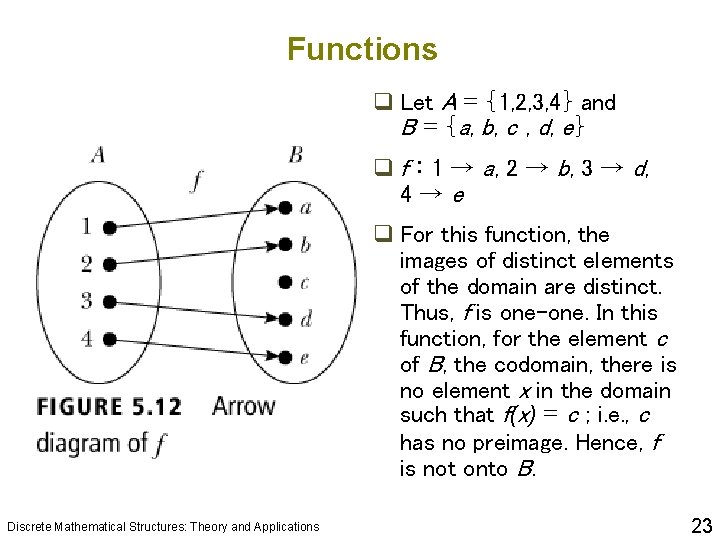
Functions q Let A = {1, 2, 3, 4} and B = {a, b, c , d, e} q f : 1 → a , 2 → b, 3 → d, 4→e q For this function, the images of distinct elements of the domain are distinct. Thus, f is one-one. In this function, for the element c of B, the codomain, there is no element x in the domain such that f(x) = c ; i. e. , c has no preimage. Hence, f is not onto B. Discrete Mathematical Structures: Theory and Applications 23

Functions Discrete Mathematical Structures: Theory and Applications 24

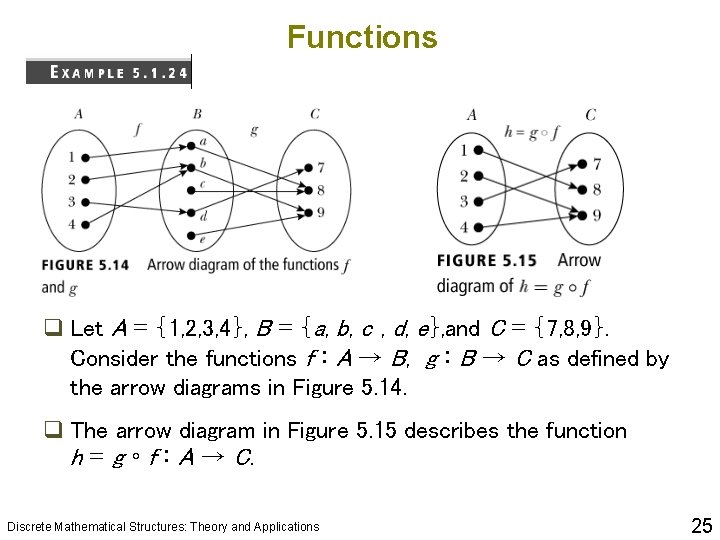
Functions q Let A = {1, 2, 3, 4}, B = {a, b, c , d, e}, and C = {7, 8, 9}. Consider the functions f : A → B, g : B → C as defined by the arrow diagrams in Figure 5. 14. q The arrow diagram in Figure 5. 15 describes the function h = g ◦ f : A → C. Discrete Mathematical Structures: Theory and Applications 25

Functions Discrete Mathematical Structures: Theory and Applications 26

Functions Discrete Mathematical Structures: Theory and Applications 27