Chapter 5 Functions and their Graphs Function Notation

Chapter 5 Functions and their Graphs

Function Notation f(t) = h Independent Variable Dependent Variable Example h = f(t) = 1454 – 16 t 2 When t= 1, h= f(1)= 1438, We read as “f of 1 equals 1438” When t = 2, h = f(2) =1390, We read as” f of 1 equals 1390 “

Ch 5. 1 (pg 251) Definition and Notation Example –To rent a plane flying lessons cost $ 800 plus $30 per hour Suppose C = 30 t + 800 (t > 0) When t = 0, C = 30(0) + 800= 800 When t = 4, C = 30(4) + 800 = 920 When t = 10, C = 30(10) + 800 = 1100 Table Ordered Pair t c 0 800 (0, 800) 4 920 (4, 920) 10 1100 (10, 1100) (t, c) The variable t in Equation is called the independent variable, and C is the dependent variable, because its values are determined by the value of t This type of relationship is called a function A function is a relationship between two variables for which a unique value of the dependent variable can be determined from a value of the independent variable

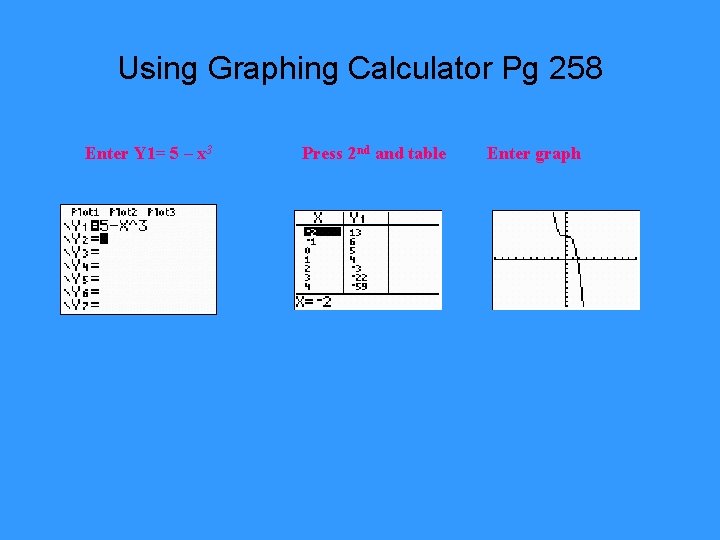
Using Graphing Calculator Pg 258 Enter Y 1= 5 – x 3 Press 2 nd and table Enter graph

Ex 5. 1, pg 264 -265 No. 40 g(t) = 5 t – 3 a) g(1) = 5(1) – 3 = 2 b) g(-4) = 5(-4) – 3 = -20 – 3= -23 c) g(14. 1) = 5( 14. 1) – 3= 70. 5 – 3= 67. 5 d) g = 5 – 3 = - 3 = No. 51. The velocity of a car that brakes suddenly can be determined from the length of its skid marks, d, by v(d) = , where d is in feet and v is in miles per hour. Complete the table of values. Solution. V(20) Similarly put all values of d and find v d 20 50 80 100 v 15. 5 24. 5 31. 0 34. 6

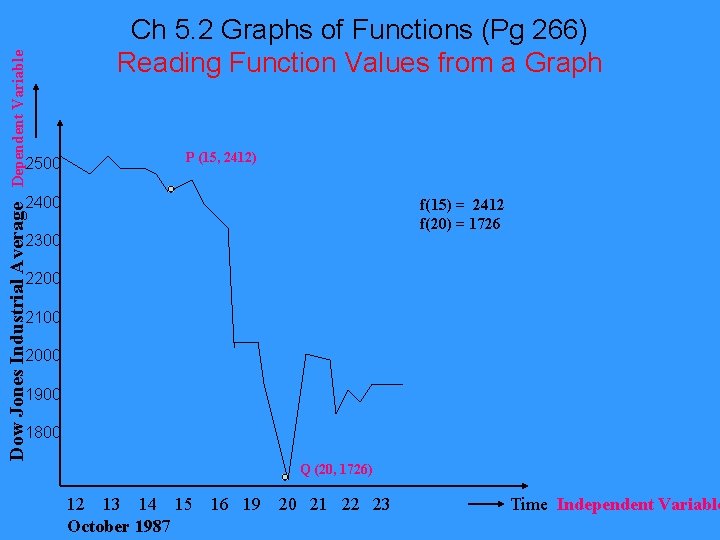
Dependent Variable 2500 Ch 5. 2 Graphs of Functions (Pg 266) Reading Function Values from a Graph P (15, 2412) 2400 Dow Jones Industrial Average f(15) = 2412 f(20) = 1726 2300 2200 2100 2000 1900 1800 Q (20, 1726) 12 13 14 15 October 1987 16 19 20 21 22 23 Time Independent Variable

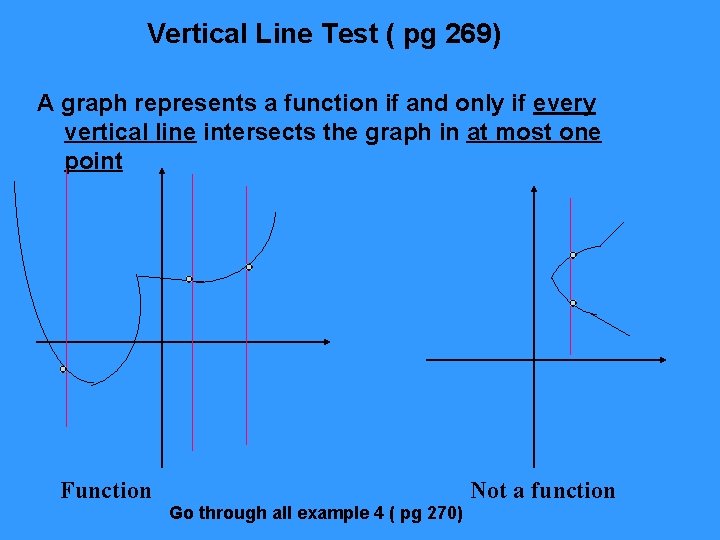
Vertical Line Test ( pg 269) A graph represents a function if and only if every vertical line intersects the graph in at most one point Function Go through all example 4 ( pg 270) Not a function

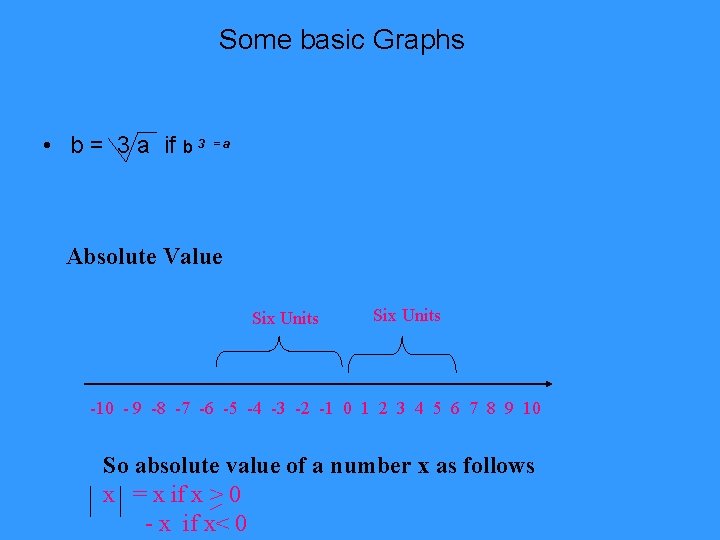
Some basic Graphs • b = 3 a if b 3 =a Absolute Value Six Units -10 - 9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 So absolute value of a number x as follows x = x if x > 0 - x if x< 0

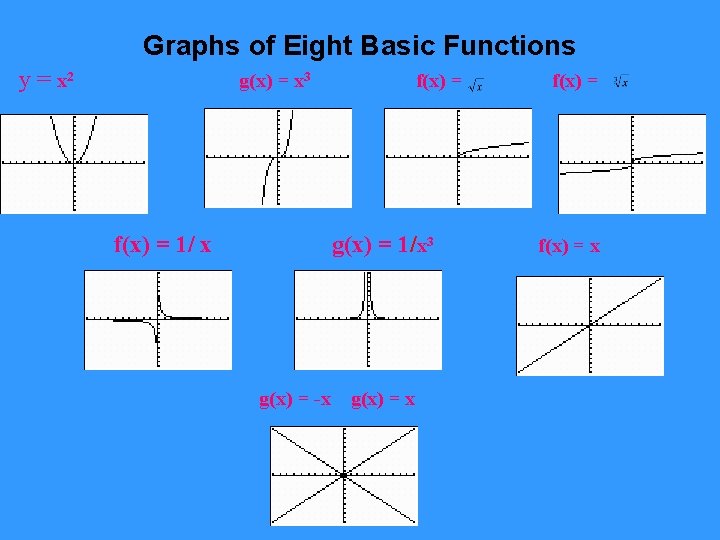
Graphs of Eight Basic Functions y = x 2 g(x) = x 3 f(x) = 1/ x f(x) = g(x) = 1/x 3 g(x) = -x g(x) = x f(x) = x

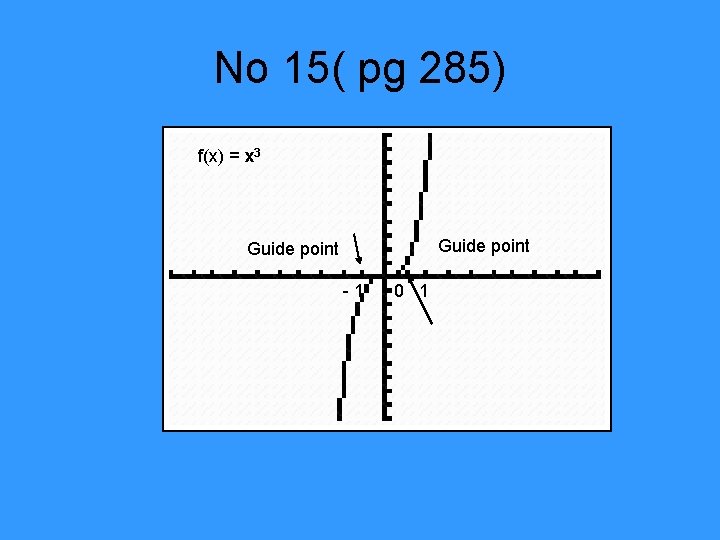
No 15( pg 285) f(x) = x 3 Guide point -1 0 1

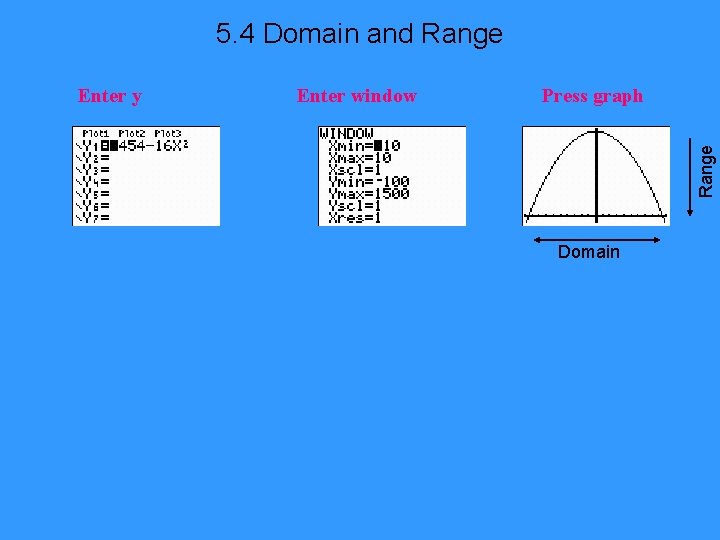
5. 4 Domain and Range Enter window Press graph Range Enter y Domain

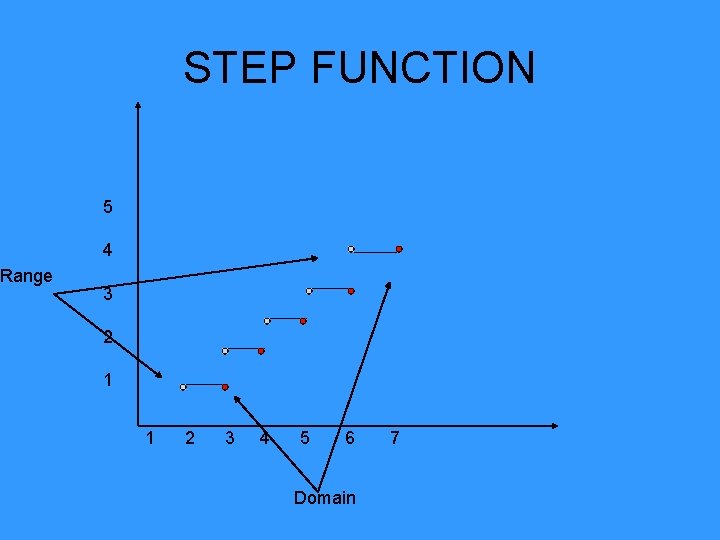
Range STEP FUNCTION 5 4 3 2 1 1 2 3 4 5 6 Domain 7

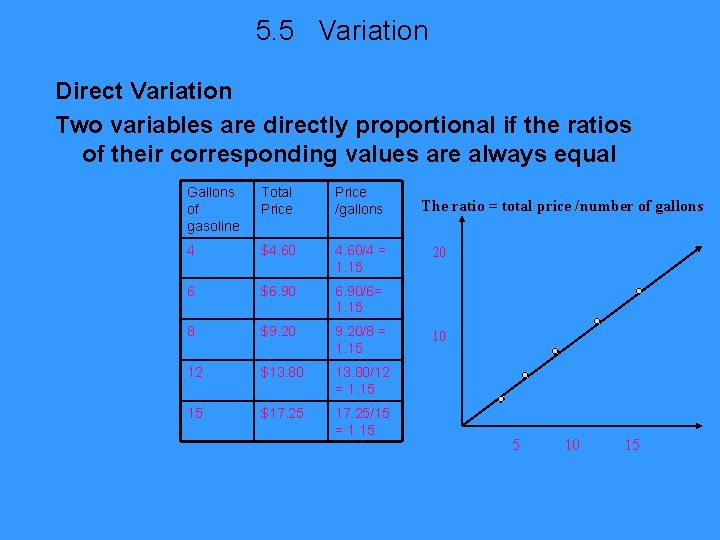
5. 5 Variation Direct Variation Two variables are directly proportional if the ratios of their corresponding values are always equal Gallons of gasoline Total Price /gallons 4 $4. 60/4 = 1. 15 6 $6. 90/6= 1. 15 8 $9. 20/8 = 1. 15 12 $13. 80/12 = 1. 15 15 $17. 25/15 = 1. 15 The ratio = total price /number of gallons 20 10 5 10 15

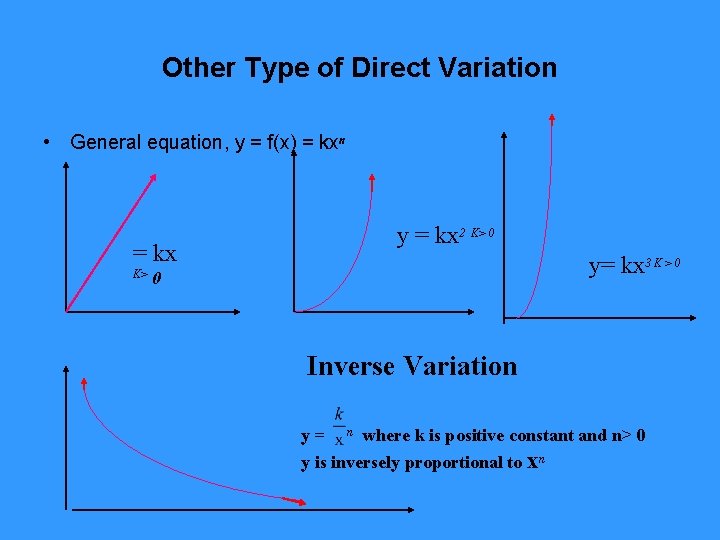
Other Type of Direct Variation • General equation, y = f(x) = kxn y = kx 2 K> 0 = kx K> y= kx 3 K > 0 0 Inverse Variation y= n where k is positive constant and n> 0 y is inversely proportional to xn

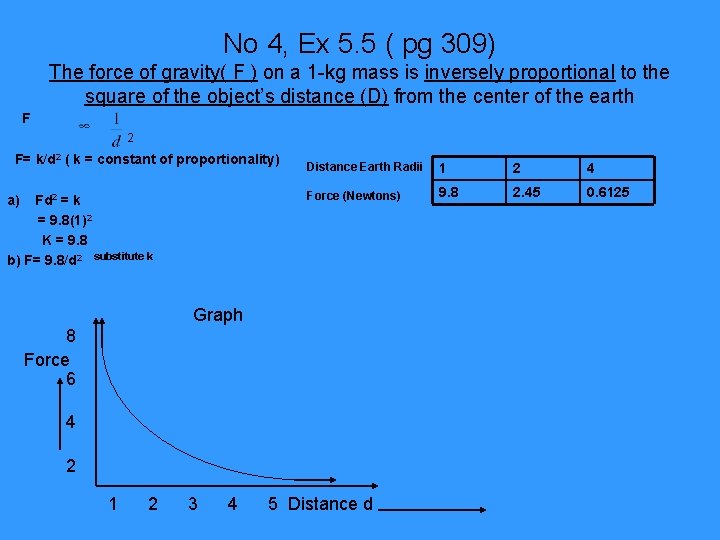
No 4, Ex 5. 5 ( pg 309) The force of gravity( F ) on a 1 -kg mass is inversely proportional to the square of the object’s distance (D) from the center of the earth F 2 F= k/d 2 ( k = constant of proportionality) a) Fd 2 = k = 9. 8(1)2 K = 9. 8 b) F= 9. 8/d 2 substitute k Distance Earth Radii 1 2 4 Force (Newtons) 9. 8 2. 45 0. 6125 Graph 8 Force 6 4 2 1 2 3 4 5 Distance d

Pg 311, No 11 The weight of an object on the moon varies directly with its weight on earth d) a) m w where m = weight of object, on moon and w= wt. Of object on earth m = kw m = 24. 75 pounds, w = 150 pounds K = 24. 75/150 = 0. 165 m = 0. 165 w , substitute k Wt. on earth (W) w 100 150 200 400 m 16. 5 24. 75 33 66 b) m = 0. 165( 120) = 19. 8 pounds c) w= m/k = 30/0. 165 = 303. 03 pound Wt. on moon (m)

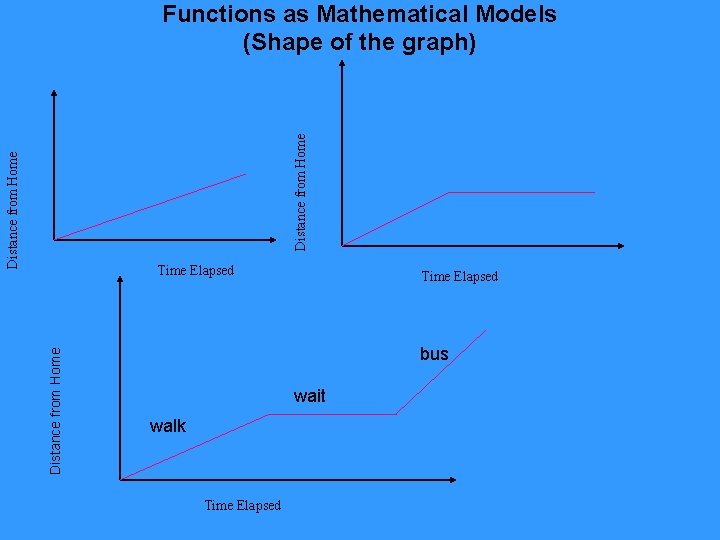
Distance from Home Functions as Mathematical Models (Shape of the graph) Distance from Home Time Elapsed bus wait walk Time Elapsed

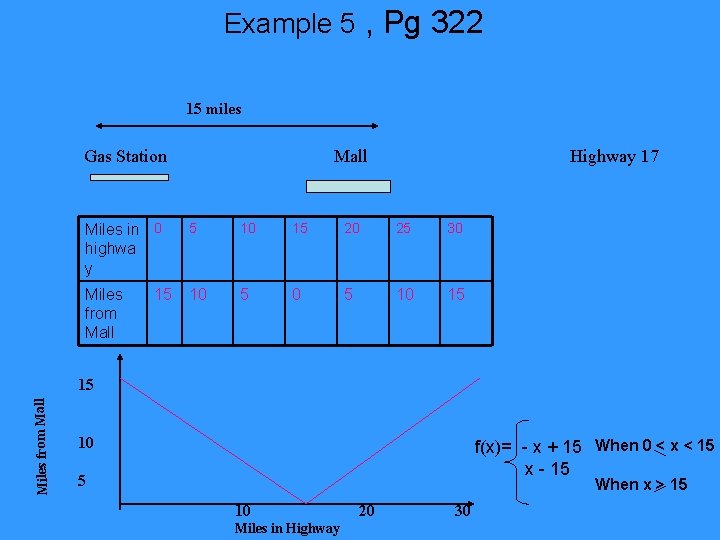
Example 5 , Pg 322 15 miles Gas Station Mall Highway 17 Miles in 0 highwa y 5 10 15 20 25 30 Miles from Mall 10 5 10 15 15 Miles from Mall 15 10 f(x)= - x + 15 When 0 < x < 15 x - 15 5 When x > 15 10 Miles in Highway 20 30

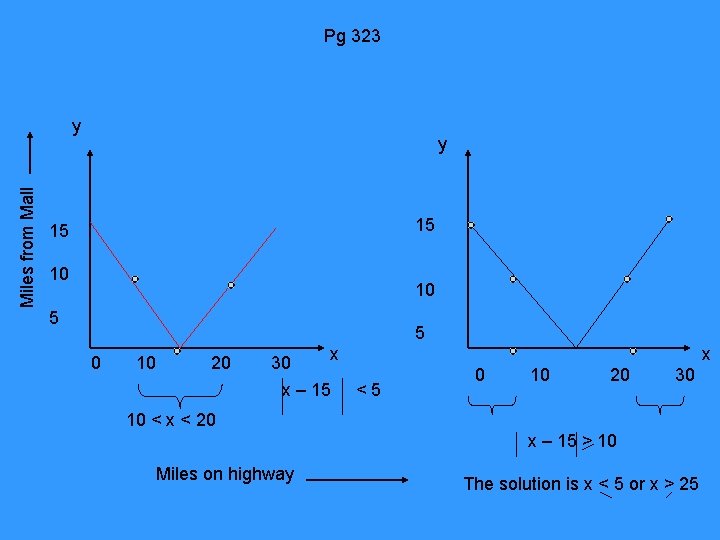
Pg 323 Miles from Mall y y 15 15 10 10 5 5 0 10 20 x 30 x – 15 < 5 x 0 10 20 30 10 < x < 20 x – 15 > 10 Miles on highway The solution is x < 5 or x > 25