Chapter 5 FLUID DYNAMIC CLASSIFICATION OF FLUID FLOW

Chapter 5 FLUID DYNAMIC

CLASSIFICATION OF FLUID FLOW 1) Viscous vs Inviscid Regions of flow Viscous flows: Flows in which the frictional effects are significant. Inviscid/nonviscous/frictionless flow regions: In many flows of practical interest, there are regions (typically regions not close to solid surfaces or no shearing stress) where viscous forces are negligibly small compared to inertial or pressure forces. The flow of an originally uniform fluid stream over a flat plate, and the regions of viscous flow (next to the plate on both sides) and inviscid flow (away from the plate). 2

2) Compressible vs Incompressible flow • A flow is classified as incompressible if the density remains nearly constant. • Liquid flows are typically incompressible. • Gas flows are often compressible, especially for high speeds. 3

3) Natural vs Forced Flow Natural – fluid flow due to natural mean such as buoyancy effect. Forced – fluid motion due to external mean such as pump or fan. • Water flow in a pipe is internal flow, and airflow over a ball is external flow. External flow over a tennis ball, and the turbulent wake region behind. • The flow of liquids in a duct is called openchannel flow if the duct is only partially filled with the liquid and there is a free surface. 4

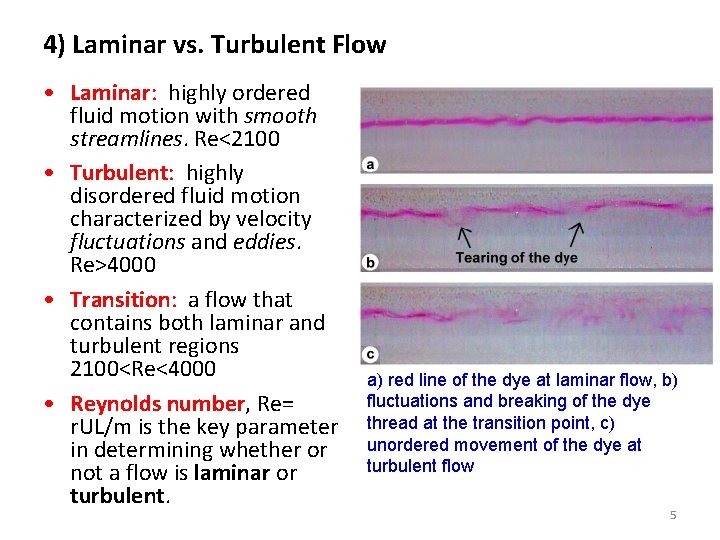
4) Laminar vs. Turbulent Flow • Laminar: highly ordered fluid motion with smooth streamlines. Re<2100 • Turbulent: highly disordered fluid motion characterized by velocity fluctuations and eddies. Re>4000 • Transition: a flow that contains both laminar and turbulent regions 2100<Re<4000 • Reynolds number, Re= r. UL/m is the key parameter in determining whether or not a flow is laminar or turbulent. a) red line of the dye at laminar flow, b) fluctuations and breaking of the dye thread at the transition point, c) unordered movement of the dye at turbulent flow 5

5) Uniform Flow, Steady Flow uniform flow: If the flow velocity is the same magnitude and direction at every point in the fluid it is said to be uniform. non-uniform: The velocity is not the same at every point the flow is non-uniform. 6

steady: A steady flow is one in which the conditions (velocity, pressure and cross-section) may differ from point to point but DO NOT change with time unsteady: If at any point in the fluid, the conditions change with time, the flow is described as unsteady. (In practise there is always slight variations in velocity and pressure, but if the average values are constant, the flow is considered steady. 7

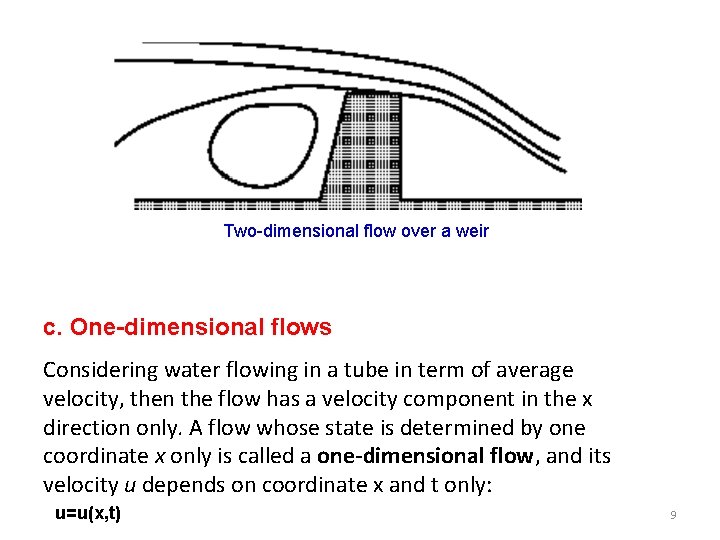
6) One-, Two-, and Three-Dimensional Flows a. Three –dimensional flows All general flows such as a ball flying in the air and a flow around a moving automobile have velocity components in x, y and z directions in the x, y and z axial directions as u, v and w, then u=u(x, y, z, t) v=v(x, y, z, t) w=w(x, y, z, t) b. Two-dimensional flows Consider water running between two parallel plates cross-cut vertically to the plates and parallel to the flow. If the flow states are the same on all planes parallel to the cut plane, the flow is called a two-dimensional flow since it can be described by two coordinates x and y. Expressing the velocity components in the x and y directions as u and v respectively, then u=u(x, y, t) v=v(x, y, t) 8

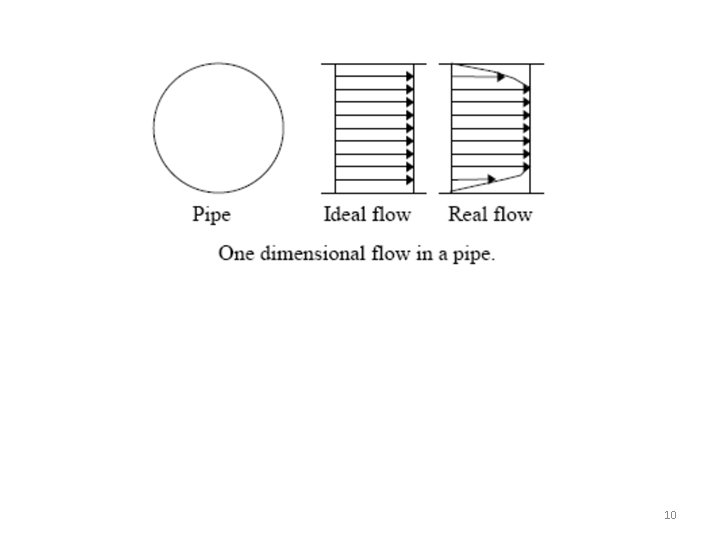
Two-dimensional flow over a weir c. One-dimensional flows Considering water flowing in a tube in term of average velocity, then the flow has a velocity component in the x direction only. A flow whose state is determined by one coordinate x only is called a one-dimensional flow, and its velocity u depends on coordinate x and t only: u=u(x, t) 9

10

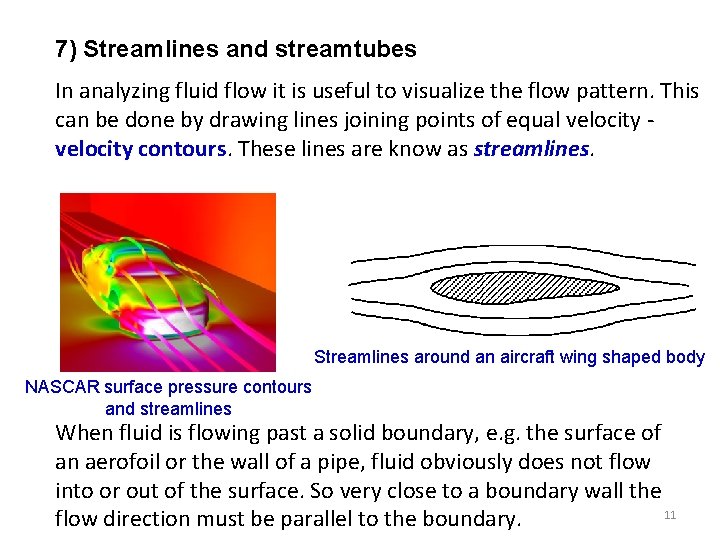
7) Streamlines and streamtubes In analyzing fluid flow it is useful to visualize the flow pattern. This can be done by drawing lines joining points of equal velocity contours. These lines are know as streamlines. Streamlines around an aircraft wing shaped body NASCAR surface pressure contours and streamlines When fluid is flowing past a solid boundary, e. g. the surface of an aerofoil or the wall of a pipe, fluid obviously does not flow into or out of the surface. So very close to a boundary wall the 11 flow direction must be parallel to the boundary.

Close to a solid boundary streamlines are parallel to that boundary At all points the direction of the streamline is the direction of the fluid velocity: this is how they are defined. Close to the wall the velocity is parallel to the wall so the streamline is also parallel to the wall. It is also important to recognize that the position of streamlines can change with time - this is the case in unsteady flow. In steady flow, the position of streamlines does not change. Some things to know about streamlines · Because the fluid is moving in the same direction as the streamlines, fluid can not cross a streamline. · Streamlines can not cross each other. If they were to cross this would indicate two different velocities at the same point. This is not physically possible. · The above point implies that any particles of fluid starting on one streamline will stay on that same streamline throughout the fluid. 12

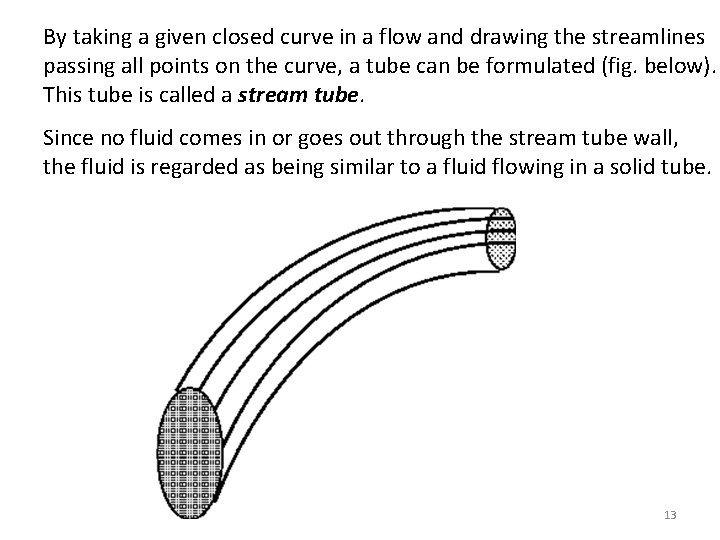
By taking a given closed curve in a flow and drawing the streamlines passing all points on the curve, a tube can be formulated (fig. below). This tube is called a stream tube. Since no fluid comes in or goes out through the stream tube wall, the fluid is regarded as being similar to a fluid flowing in a solid tube. 13

And in a two-dimensional flow we have a streamtube which is flat (in the plane of the paper): The "walls" of a streamtube are made of streamlines. As we have seen above, fluid cannot flow across a streamline, so fluid cannot cross a streamtube wall. The streamtube can often be viewed as a solid walled pipe. A streamtube is not a pipe - it differs in unsteady flow as the walls will move with time. And it differs because the "wall" is moving with the fluid. 14

Fluid Flow Rate 1) Mass flow rate 2) Volume flow rate A is area of section, v is the average velocity/mean velocity of flow 3) Weight flow rate Ɣ is specific weight ( weight/volume) 15

Continuity Matter cannot be created or destroyed - (it is simply changed in to a different form of matter). This principle is know as the conservation of mass and we use it in the analysis of flowing fluids. The principle is applied to fixed volumes, known as control volumes (or surfaces), like that in the figure below: An arbitrarily shaped control volume. 16

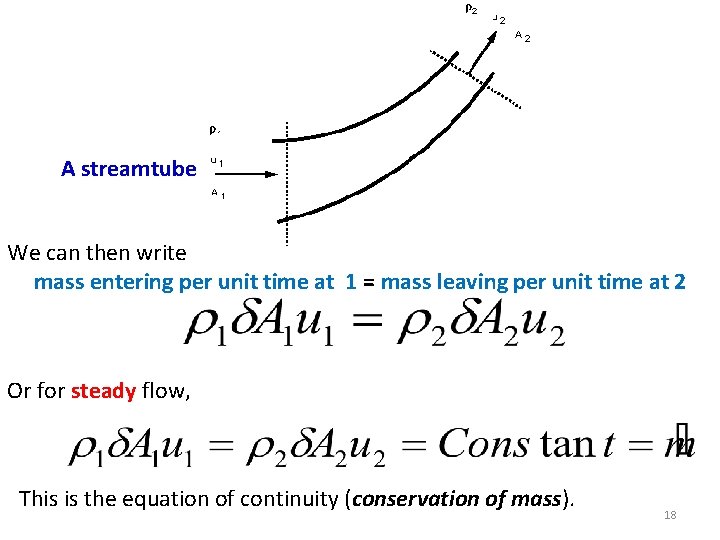
For any control volume the principle of conservation of mass says Mass entering per unit time = Mass leaving per unit time + Increase of mass in the control volume per unit time For steady flow there is no increase in the mass within the control volume, so For steady flow Mass entering per unit time = Mass leaving per unit time This can be applied to a streamtube such as that shown in next slide. No fluid flows across the boundary made by the streamlines so mass only enters and leaves through the two ends of this streamtube section. 17

A streamtube We can then write mass entering per unit time at 1 = mass leaving per unit time at 2 Or for steady flow, This is the equation of continuity (conservation of mass). 18

The flow of fluid through a real pipe (or any other vessel) will vary due to the presence of a wall - in this case we can use the mean velocity and write When the fluid can be considered incompressible, i. e. the density does not change, so (dropping the m subscript) 19

EXAMPLE If the area A 1 = 10 10 -3 m 2 and A 2 = 3 10 -3 m 2 and the upstream mean velocity, v 1=2. 1 m/s, calculate the downstream mean velocity. Solution to Example 4. 4 Now try this on a diffuser, a pipe which expands or diverges as in the figure below. Section 1 Section 2 Figure 4. 3 20

EXAMPLE Referring to the Figure the diameter at section 1 is d 1 = 30 mm and at section 2 is d 2=40 mm and the mean velocity at section 2 is v 2 = 3. 0 m/s. Calculate the velocity entering the diffuser. Solution to Example 4. 5 The downstream velocity only changes from the upstream by the ratio of the two areas of the pipe. As the area of the circular pipe is a function of the diameter, we can reduce the calculation further. Thus, 21

Another example of the use of the continuity principle is to determine the velocities in pipes coming from a junction. Total mass flow into the junction = Total mass flow out of the junction When the flow is incompressible (e. g. if it is water) 22

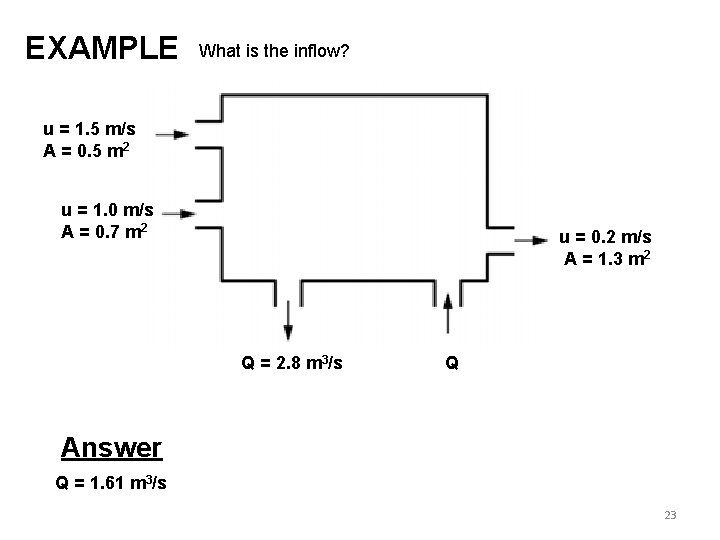
EXAMPLE What is the inflow? u = 1. 5 m/s A = 0. 5 m 2 u = 1. 0 m/s A = 0. 7 m 2 u = 0. 2 m/s A = 1. 3 m 2 Q = 2. 8 m 3/s Q Answer Q = 1. 61 m 3/s 23

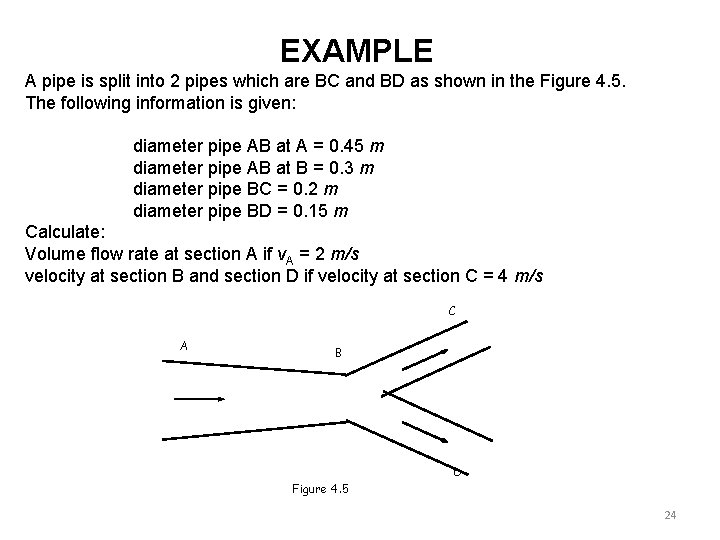
EXAMPLE A pipe is split into 2 pipes which are BC and BD as shown in the Figure 4. 5. The following information is given: diameter pipe AB at A = 0. 45 m diameter pipe AB at B = 0. 3 m diameter pipe BC = 0. 2 m diameter pipe BD = 0. 15 m Calculate: Volume flow rate at section A if v. A = 2 m/s velocity at section B and section D if velocity at section C = 4 m/s C A B D Figure 4. 5 24

a)Volume flow rate at section A b) Volume flow rate at section A = Volume flow rate at section B 25

BERNOULLI’S EQUATION • Daniel Bernoulli 1700 -1782 • Merchant, Doctor, Mathematician • Investigated the forces present in a moving fluid and develop “BERNOULLI’S EQUATION” 26

Bernoulli equation is an approximate relation between pressure, velocity, and elevation, and is valid in regions of steady, incompressible flow where net frictional forces are negligible. The Bernoulli approximation is typically useful in flow regions outside of boundary layers (solid wall) and wakes (downstream of bodies), where the fluid motion is governed by the combined effects of pressure and gravity forces. Conservation of Linear Momentum Principle-derivation of Bernoulli equation. The Bernoulli equation is an approximate equation that is valid only in inviscid regions of flow where net viscous forces are negligibly small compared to inertial, gravitational, or pressure forces. Such regions occur outside of boundary layers and wakes. 27

Limitations on the Use of the Bernoulli Equation Steady flow The quantity of fluid flowing past any section to another section at a constant rate. No velocity change with time at a specific location. Thus, acceleration is due to the change of velocity with location only. Incompressible flow ρ = constant. The specific weight of the fluid is assumed to be the same at the two sections of interest. Frictionless/nonviscous/inviscid flow Every flow involves some friction, no matter how small, and frictional effects may or may not be negligible. Frictional effects and components that disturb the streamlined structure of flow in a flow section make the Bernoulli equation invalid. It should not be used in any of the flows shown here.

There can be no mechanical devices (pump, turbine, fan, or any other machine or impeller since such devices destroy the streamlines and carry out energy interactions with the fluid particles) between the two sections of interest that would add energy to/remove energy from the system, because the equation states that the total energy in the fluid is constant. There can be no heat transferred into/out of the fluid. Flow along a streamline Strictly speaking, the Bernoulli equation is applicable along a streamline(not conditions on two different streamlines). However, when a region of the flow is irrotational (i. e. , the fluid particles do not “spin” as they move) and there is negligibly small vorticity in the flow field, the Bernoulli equation becomes applicable across streamlines as well. When the flow is irrotational, the Bernoulli equation becomes applicable between any two points along the flow (not just on the same streamline). 29

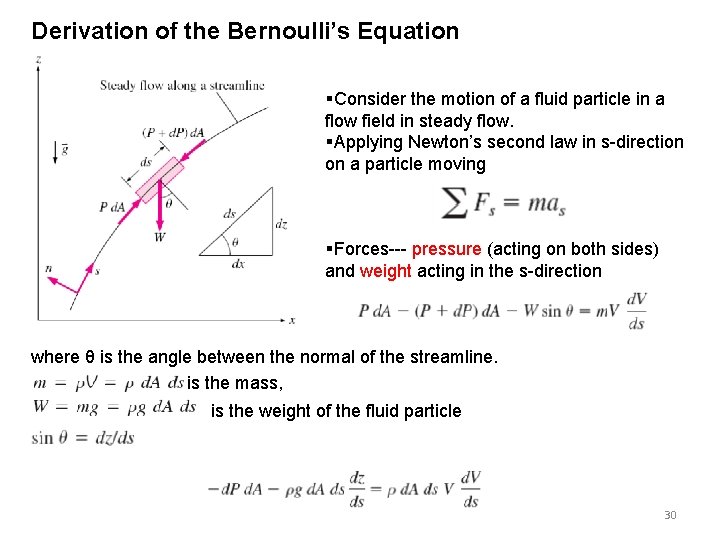
Derivation of the Bernoulli’s Equation §Consider the motion of a fluid particle in a flow field in steady flow. §Applying Newton’s second law in s-direction on a particle moving §Forces--- pressure (acting on both sides) and weight acting in the s-direction where θ is the angle between the normal of the streamline. is the mass, is the weight of the fluid particle 30

Canceling d. A from Vd. V = ½ d(V 2) and dividing by ρ The last two term are exact differentials. In case Steady, incompressible flow , the first term also becomes an exact differential, and integration gives Potential energy Flow energy Kinetic energy The sum of the kinetic, potential, and flow energies of a fluid particle is constant along a streamline during steady flow when compressibility and frictional effects are negligible. 31

As stated above, the Bernoulli equation applies to conditions along a streamline. We can apply it between two points, 1 and 2, on the streamline in the figure below Two points joined by a streamline total energy per unit weight at 1 = total energy per unit weight at 2 or total head at 1 = total head at 2 or total pressure at 1 = total pressure at 2 Dynamic pressure (pressure rise when fluid in motion) Static pressure (pressure when the fluid is not in motion) hydrostatic pressure (fluid weight) 32

Practical use of the Bernoulli Equation The Bernoulli equation is often combined with the continuity equation to find velocities and pressures at points in the flow connected by a streamline. Example: Finding pressures and velocities within a contracting and expanding pipe. 33

A fluid, density ρ= 960 kg/m 3 is flowing steadily through the above tube. The section diameters are d 1=100 mm and d 2=80 mm. The gauge pressure at 1 is P 1=200 k. N/m 2 The velocity at 1 is u 1=5 m/s. The tube is horizontal (z 1=z 2) Apply the Bernoulli equation along a streamline joining section 1 with section 2. 34

Use the continuity equation to find u 2 So pressure at section 2 35

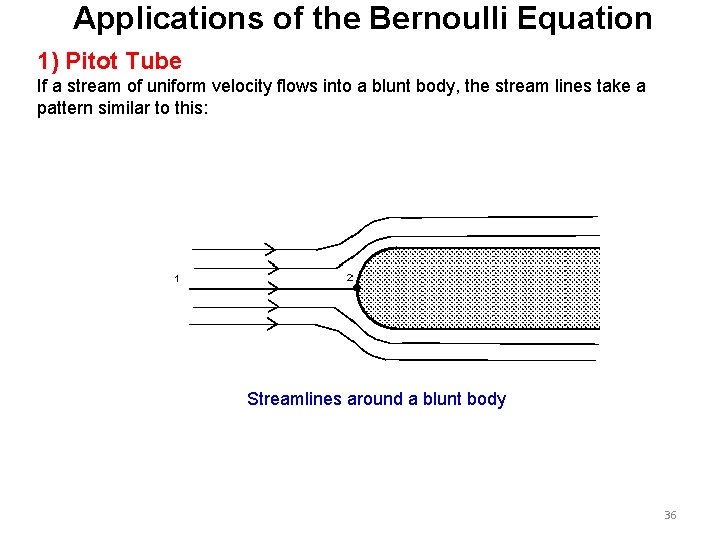
Applications of the Bernoulli Equation 1) Pitot Tube If a stream of uniform velocity flows into a blunt body, the stream lines take a pattern similar to this: Streamlines around a blunt body 36

Note how some move to the left and some to the right. But one, in the centre, goes to the tip of the blunt body and stops. It stops because at this point the velocity is zero - the fluid does not move at this one point. This point is known as the stagnation point. From the Bernoulli equation we can calculate the pressure at this point. Apply Bernoulli along the central streamline from a point upstream where the velocity is u 1 and the pressure p 1 to the stagnation point of the blunt body where the velocity is zero, u 2 = 0. Also z 1 = z 2. 37

This increase in pressure which bring the fluid to rest is called the dynamic pressure. or converting this to head The total pressure is know as the stagnation pressure (or total pressure) or in terms of head 38

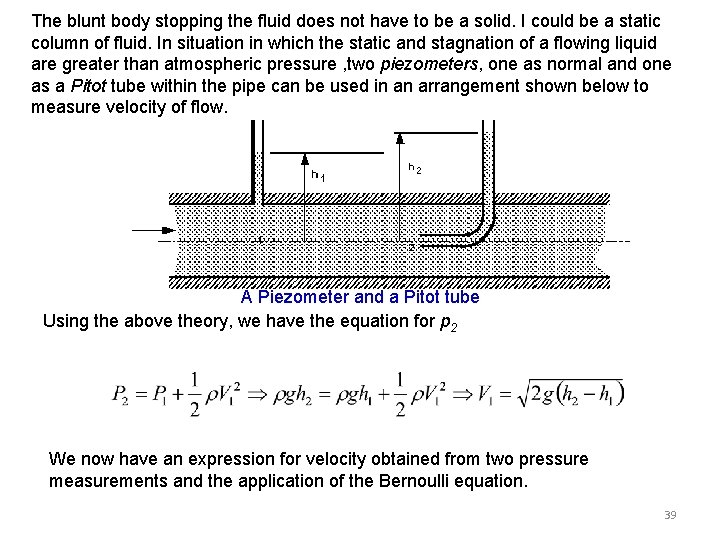
The blunt body stopping the fluid does not have to be a solid. I could be a static column of fluid. In situation in which the static and stagnation of a flowing liquid are greater than atmospheric pressure , two piezometers, one as normal and one as a Pitot tube within the pipe can be used in an arrangement shown below to measure velocity of flow. A Piezometer and a Pitot tube Using the above theory, we have the equation for p 2 We now have an expression for velocity obtained from two pressure measurements and the application of the Bernoulli equation. 39

EXAMPLE In water treatment plant it is required to monitor the maximum velocity in the water mains. A pitot-tube is inserted in the centre of the pipe and connected to two piezometer tubes. If the differential pressure head is 250 mm, estimate the velocity of flow. Answer: 2. 21 m/s 40

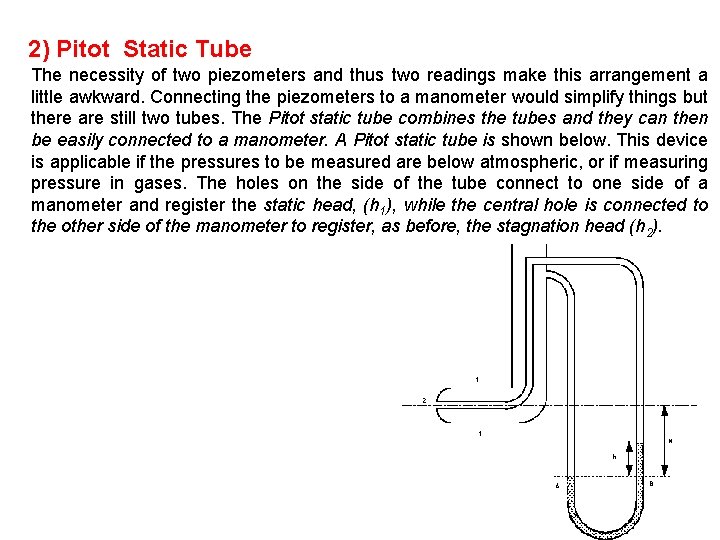
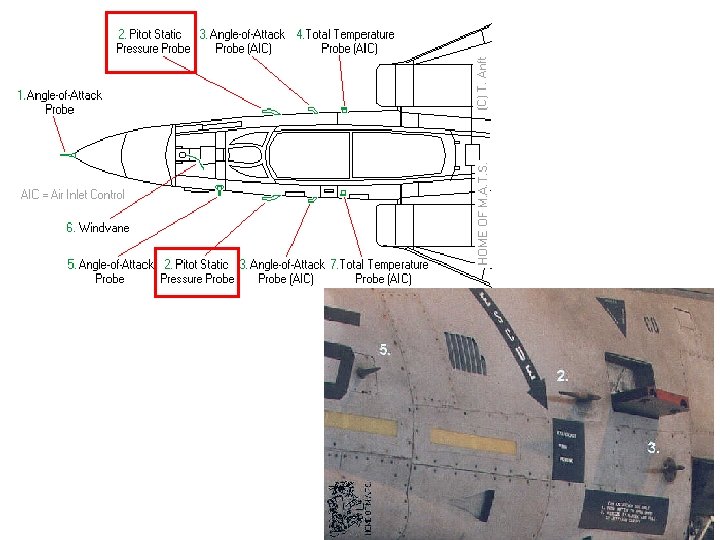
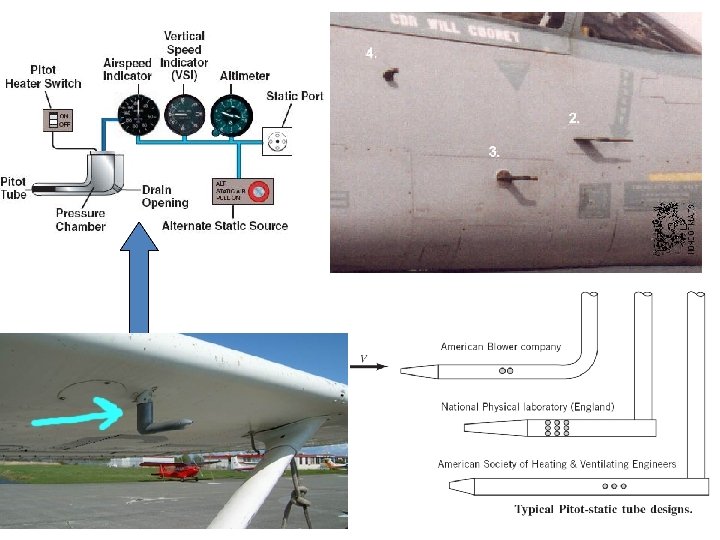
2) Pitot Static Tube The necessity of two piezometers and thus two readings make this arrangement a little awkward. Connecting the piezometers to a manometer would simplify things but there are still two tubes. The Pitot static tube combines the tubes and they can then be easily connected to a manometer. A Pitot static tube is shown below. This device is applicable if the pressures to be measured are below atmospheric, or if measuring pressure in gases. The holes on the side of the tube connect to one side of a manometer and register the static head, (h 1), while the central hole is connected to the other side of the manometer to register, as before, the stagnation head (h 2). 41

Consider the pressures on the level of the centre line of the Pitot tube and using theory of the manometer, We know that , substituting this in to the above gives or 42

43

44

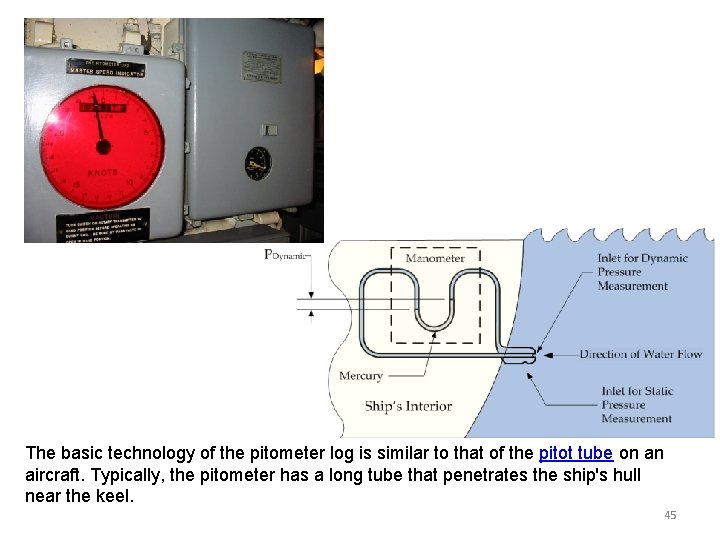
The basic technology of the pitometer log is similar to that of the pitot tube on an aircraft. Typically, the pitometer has a long tube that penetrates the ship's hull near the keel. 45

EXAMPLE A Pitot-static probe is used to measure the velocity of an aircraft flying at 3000 m(ρ = 0. 909 kg/m 3). If the differential pressure reading is 3 k. Pa, determine the velocity of the aircraft. Answer: 81. 2 m/s 46

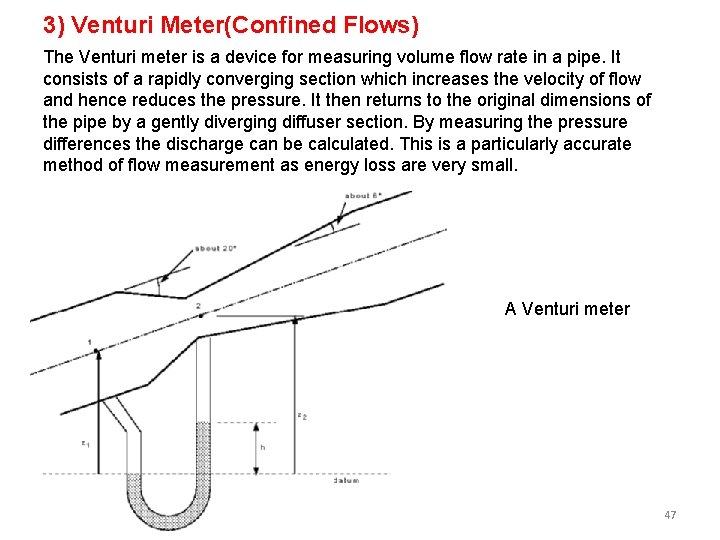
3) Venturi Meter(Confined Flows) The Venturi meter is a device for measuring volume flow rate in a pipe. It consists of a rapidly converging section which increases the velocity of flow and hence reduces the pressure. It then returns to the original dimensions of the pipe by a gently diverging diffuser section. By measuring the pressure differences the discharge can be calculated. This is a particularly accurate method of flow measurement as energy loss are very small. A Venturi meter 47

Applying Bernoulli along the streamline from point 1 to point 2 in the narrow throat of the Venturi meter we have By the using the continuity equation we can eliminate the velocity u 2, Substituting this into and rearranging the Bernoulli equation we get 48

To get theoretical volume flow rate this is multiplied by the area. To get the actual volume flow rate taking in to account the losses due to friction, we include a coefficient of volume flow rate 49

This can also be expressed in terms of the manometer readings Thus the discharge can be expressed in terms of the manometer reading: 50

Notice how this expression does not include any terms for the elevation or orientation (z 1 or z 2) of the Venturimeter. This means that the meter can be at any convenient angle to function. The purpose of the diffuser in a Venturi meter is to assure gradual and steady deceleration after the throat. This is designed to ensure that the pressure rises again to something near to the original value before the Venturi meter. The angle of the diffuser is usually between 6 and 8 degrees. Wider than this and the flow might separate from the walls resulting in increased friction and energy and pressure loss. If the angle is less than this the meter becomes very long and pressure losses again become significant. The efficiency of the diffuser of increasing pressure back to the original is rarely greater than 80%. Venturi meter with digital readout 51

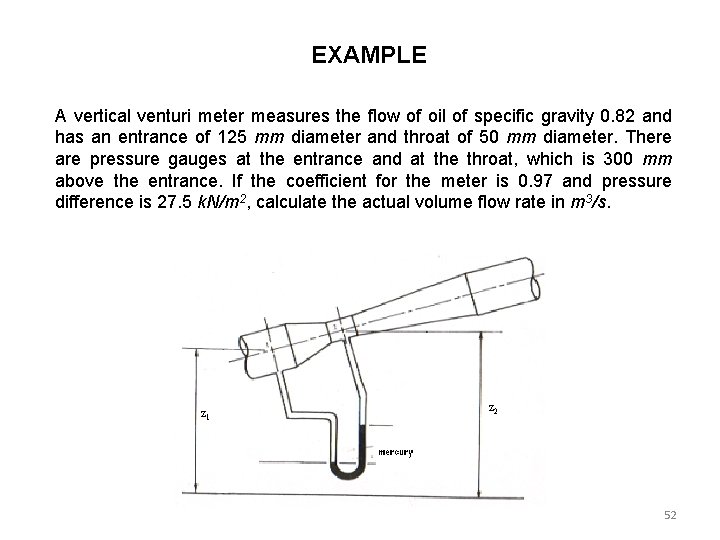
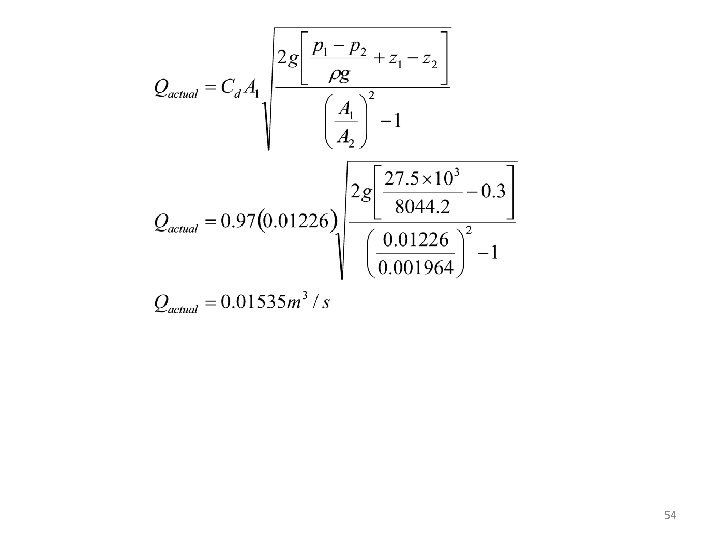
EXAMPLE A vertical venturi meter measures the flow of oil of specific gravity 0. 82 and has an entrance of 125 mm diameter and throat of 50 mm diameter. There are pressure gauges at the entrance and at the throat, which is 300 mm above the entrance. If the coefficient for the meter is 0. 97 and pressure difference is 27. 5 k. N/m 2, calculate the actual volume flow rate in m 3/s. z 1 z 2 52

SOLUTION: Cd = 0. 97 53

54

4) Flow Through A Small Orifice (Free Jet) We are to consider the flow from a tank through a hole in the side close to the base. The general arrangement and a close up of the hole and streamlines are shown in the figure below Tank and streamlines of flow out of the sharp edged orifice 55

The shape of the holes edges are as they are (sharp) to minimize frictional losses by minimizing the contact between the hole and the liquid - the only contact is the very edge. Looking at the streamlines you can see how they contract after the orifice to a minimum value when they all become parallel, at this point, the velocity and pressure are uniform across the jet. This convergence is called the vena contracta. (From the Latin. contracted vein. ). It is necessary to know the amount of contraction to allow us to calculate the flow. We can predict the velocity at the orifice using the Bernoulli equation. Apply it along the streamline joining point 1 on the surface to point 2 at the centre of the orifice. At the surface velocity is negligible (u 1 = 0) and the pressure atmospheric (p 1 = 0). At the orifice the jet is open to the air so again the pressure is atmospheric (p 2 = 0). If we take the datum line through the orifice then z 1 = h and z 2 =0, leaving 56

This is theoretical value of velocity. Unfortunately it will be an over estimate of the real velocity because friction losses have not been taken into account. To incorporate friction we use the coefficient of velocity to correct theoretical velocity, Each orifice has its own coefficient of velocity, they usually lie in the range( 0. 97 - 0. 99). To calculate the volume flow rate through the orifice we multiply the area of the jet by the velocity. The actual area of the jet is the area of the vena contracta not the area of the orifice. We obtain this area by using a coefficient of contraction for the orifice So the volume flow rate through the orifice is given by 57

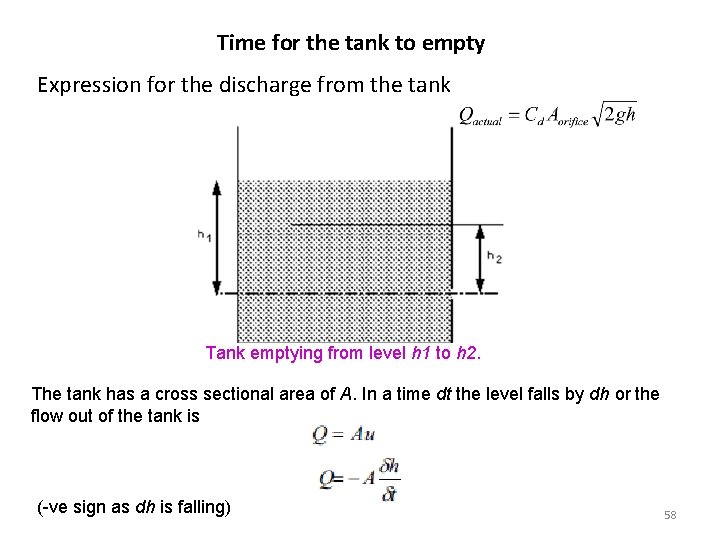
Time for the tank to empty Expression for the discharge from the tank Tank emptying from level h 1 to h 2. The tank has a cross sectional area of A. In a time dt the level falls by dh or the flow out of the tank is (-ve sign as dh is falling) 58

Rearranging and substituting the expression for Qactual through the orifice gives This can be integrated between the initial level, h 1, and final level, h 2, to give an expression for the time it takes to fall this distance 59

EXAMPLE A pressurized tank of water has a 10 cm diameter orifice at the bottom, where water discharges to the atmosphere. The water level is 3 m above the outlet. The tank air pressure above the water level is 300 k. Pa (absolute) while the atmospheric pressure is 100 k. Pa. Neglecting frictional effects, determine the initial discharge rate of water from the tank. Anw: 0. 168 m 3/s 60

SOLUTION: 61

EXAMPLE The water level in a tank is 20 m above the ground. A hose is connected to the bottom of the tank, and the nozzle at the end of the hose is pointed straight up. The tank cover is airtight, and the air pressure above the water surface is 2 atm gage. The system is at sea level. Determine the maximum height to which the water stream could rise. 62

SOLUTION: 63

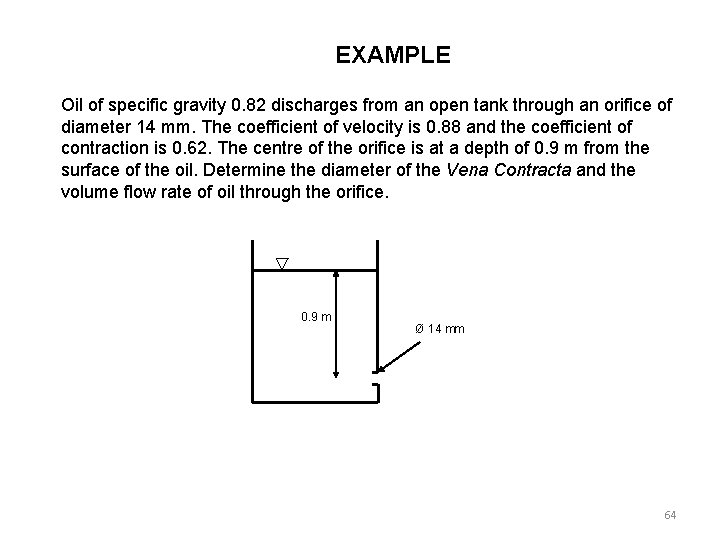
EXAMPLE Oil of specific gravity 0. 82 discharges from an open tank through an orifice of diameter 14 mm. The coefficient of velocity is 0. 88 and the coefficient of contraction is 0. 62. The centre of the orifice is at a depth of 0. 9 m from the surface of the oil. Determine the diameter of the Vena Contracta and the volume flow rate of oil through the orifice. 0. 9 m Ø 14 mm 64

SOLUTION : Data: Specific gravity = 0. 82; d = 0. 014 mm; Cv = 0. 88; Cc = 0. 62; h = 0. 9 m (a) Substituting the values, or 65

(b) Theoretical velocity Theoretical volume flow rate Coefficient of volume flow rate Actual volume flow rate = Cd x Theoretical volume flow rate 66

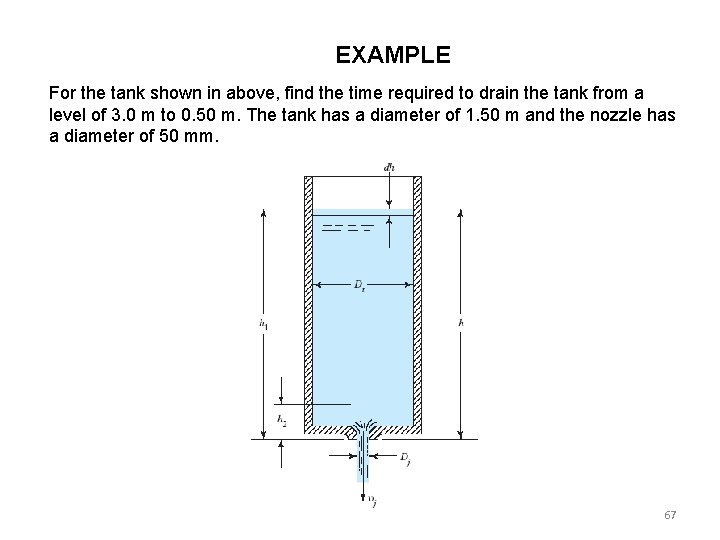
EXAMPLE For the tank shown in above, find the time required to drain the tank from a level of 3. 0 m to 0. 50 m. The tank has a diameter of 1. 50 m and the nozzle has a diameter of 50 mm. 67

SOLUTION: 68

5) SLUICE GATE(Open Channel) Slice gate is used to regulate and measure the flowrate in an open channel. The flowrate, Q, is a function of the water depth upstream, z 1, the width of the gate, b, and the gate opening, a. Application of the Bernoulli equation and continuity equation between point (1) and (2) can provide a good approximation to the flowarate obtained. Assume the velocity profile are uniform sufficiently far upstream and down stream of the gate. Thus apply the Bernoulli and continuity equations between points on the free surface at (1) and (2) to give 69

With p 1=p 2=0, theoretical flowrate In the limit of z 1>>z 2, this result simply becomes This limiting result represents the fact that if the depth ration, z 1/z 2 is large, the kinetic energy of the fluid upstream of the gate is negligible and the fluid velocity after it has fallen a distance (z 1 -z 2) z 1 is approximately As was discussed relative to flow from an orifice, the fluid cannot turn a sharp 90° corner. A vena contracta results with a contraction coefficient, Cc=z 2/a, less than 1. Typically Cc~0. 61 over the depth ratio range of 0<a/z 1<0. 2. For large value of a/z 1, the value of Cc increase rapidly. 70

Pictures of water gate 71

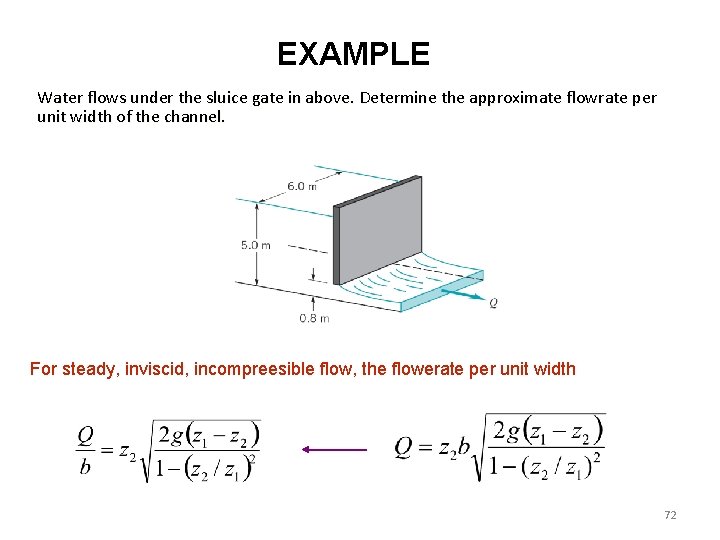
EXAMPLE Water flows under the sluice gate in above. Determine the approximate flowrate per unit width of the channel. For steady, inviscid, incompreesible flow, the flowerate per unit width 72

With z 1=5. 0 m and a=0. 80 m, so the ratio a/z 1=0. 16<0. 20. Assuming contraction coefficient is approximately Cc=0. 61. z 2=Cca=0. 61(0. 80 m)=0. 488 m. The flowrate If we consider z 1>>z 2 and neglect the kinetic energy of the upstream fluid, we would have 73

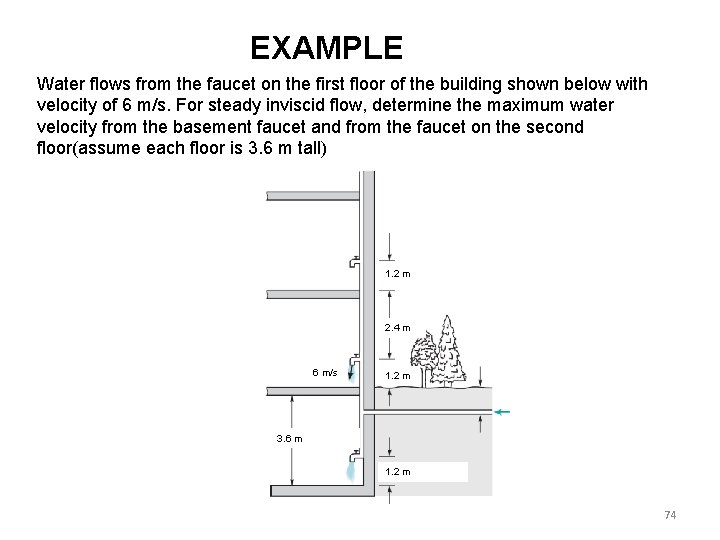
EXAMPLE Water flows from the faucet on the first floor of the building shown below with velocity of 6 m/s. For steady inviscid flow, determine the maximum water velocity from the basement faucet and from the faucet on the second floor(assume each floor is 3. 6 m tall) 1. 2 m 2. 4 m 6 m/s 1. 2 m 3. 6 m 1. 2 m 74