Chapter 5 Electrons in Atoms 1 The Development

Chapter 5 Electrons in Atoms 1

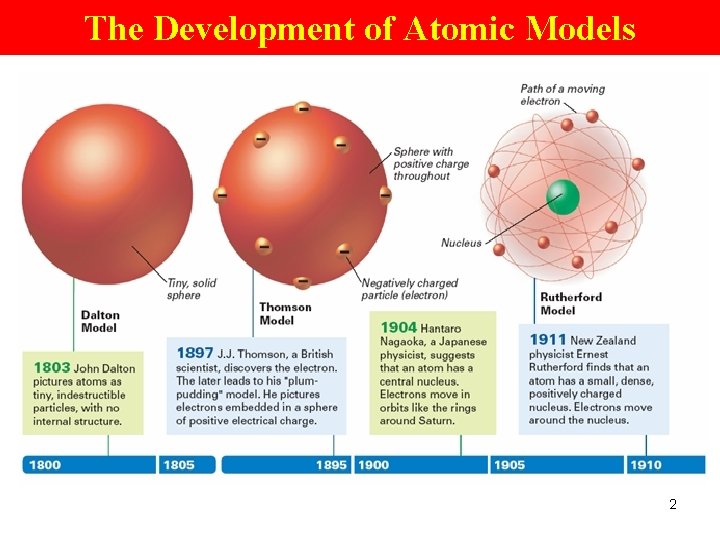
The Development of Atomic Models 2

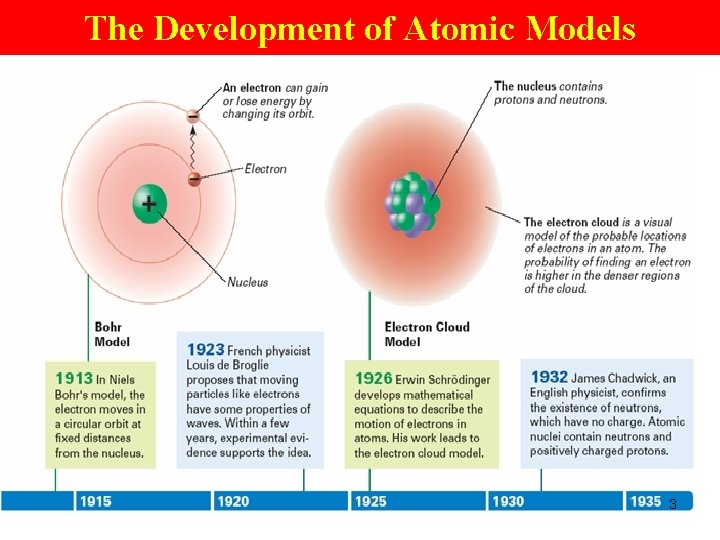
The Development of Atomic Models 3

Dalton model of Atom • tiny, indestructible particles • No internal structure 4

Thomson model Plum-pudding • Sphere with +ve charge throughout • e- embedded in a sphere of +ve electrical charge 5

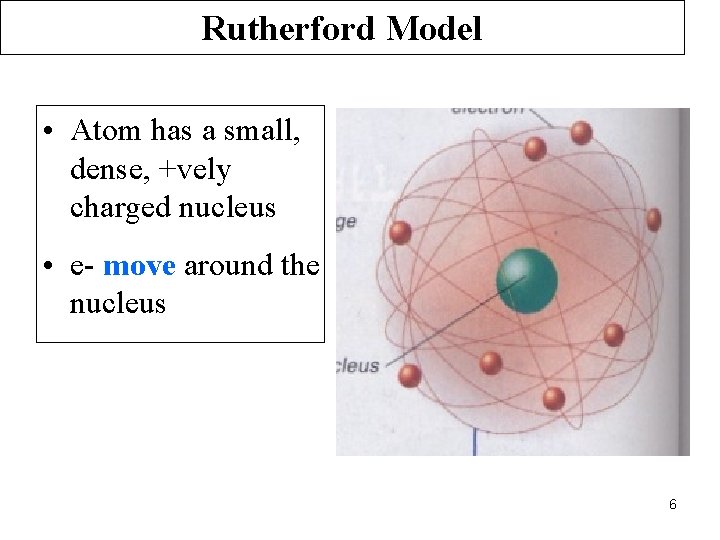
Rutherford Model • Atom has a small, dense, +vely charged nucleus • e- move around the nucleus 6

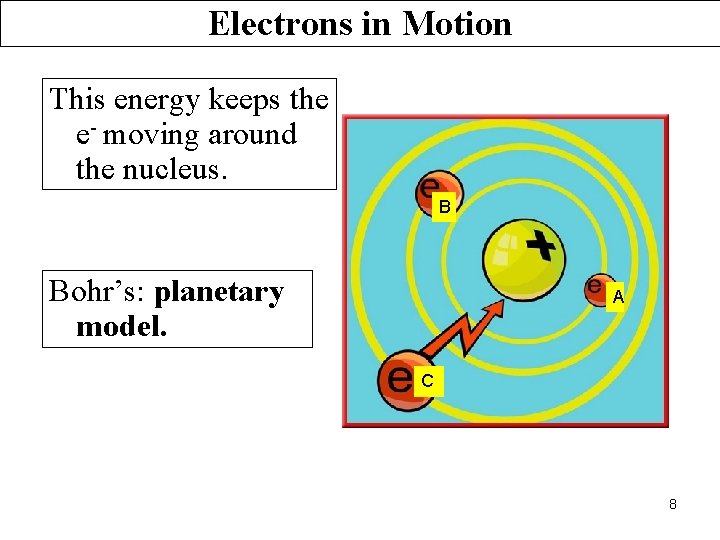
Electrons in Motion Bohr proposed that e- must have enough energy to keep them in constant motion around the nucleus. • e- have k. e. that enables them to overcome the attraction of the +ve nucleus. 7

Electrons in Motion This energy keeps the e- moving around the nucleus. B Bohr’s: planetary model. A C 8

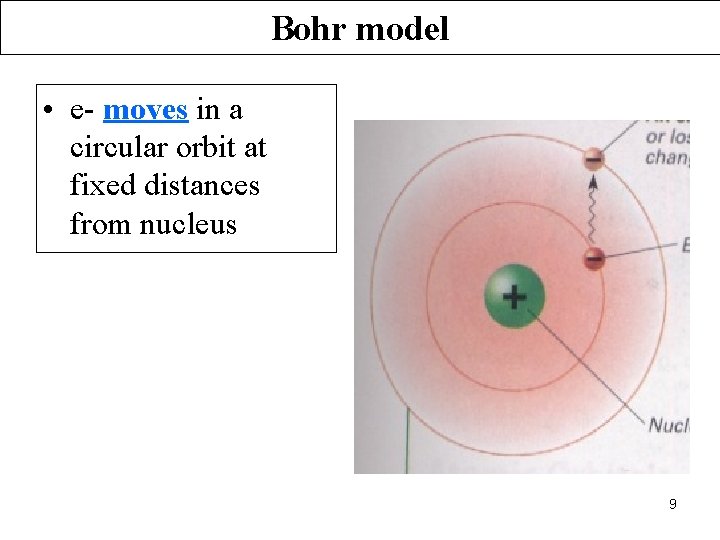
Bohr model • e- moves in a circular orbit at fixed distances from nucleus 9

Bohr Model Each possible e- orbit in Bohr’s model has a fixed energy. Energy levels: ØThe fixed energies an e- can have. A quantum of energy Ø is the amt of energy required to move 1 efrom 1 EL to a higher EL. 10

QW Under what condition will an e- jump from a lower EL to a higher EL? 11

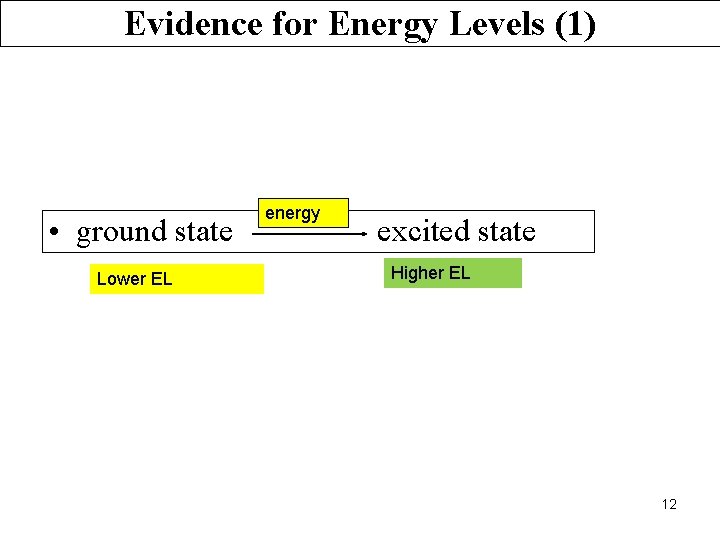
Evidence for Energy Levels (1) • ground state Lower EL energy excited state Higher EL 12

e- Arrangement in Atoms • If this rock were to tumble over, it would end up at a lower height. It would have less energy than before, but its position would be more stable. • Energy and stability play an important role in determining how e- are configured in an atom. 13

Evidence for Energy Levels (2) Bohr: • e- can have only certain amts of energy (k. e. ) • move around the nucleus • only at distances that correspond to those amts of energy. Energy levels • regions of space in which e- can move about the nucleus of an atom. 14

e- Cloud Model • EL are not neat, planetlike orbits around the nucleus of an atom. • Instead, …‘ 3 -d’ regions of space around the nucleus in which e- are most likely to be found. 15

e- Cloud Model • e- themselves take up little space but travel rapidly thru the space (3 -d) surrounding the nucleus. • These ‘ 3 -d’ regions where e- travel may be depicted as clouds around the nucleus. e- cloud Ø the space around the nucleus of an atom where the e- are found. 16

Quantum Mechanical Model Ø The propeller blade has the same probability of being anywhere in the blurry region, but you cannot tell its location at any instant. (cannot see the blades when spinning 17

Quantum Mechanical Model Ø The modern description of the e- in atoms, the quantum mechanical model 18

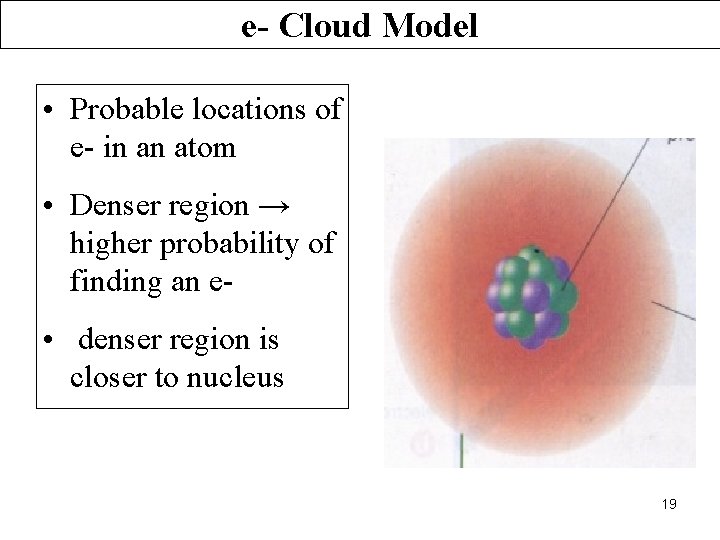
e- Cloud Model • Probable locations of e- in an atom • Denser region → higher probability of finding an e • denser region is closer to nucleus 19

Quantum Mechanical Model ØThe probability of finding an e- within a certain volume (3 -d) of space surrounding the nucleus can be represented as a fuzzy cloud. ØThe cloud is denser where the probability of finding the e- is higher. 20

Orbitals • The e- Cloud Model is based on the probability of finding an e- in a certain region of space at any given instant. • e- are distributed into sublevels and orbitals in the way that creates the most stable arrangement----lowest energy. 21

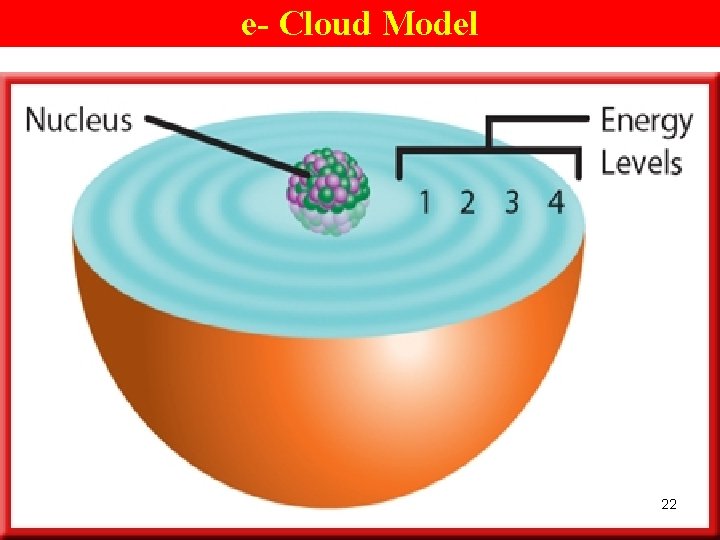
e- Cloud Model 22

Electrons in Energy Level (3) Valence e- • the e- in the outermost (highest) EL. • determine chem properties of the elements. • elements in the same gp have similar chem properties 23

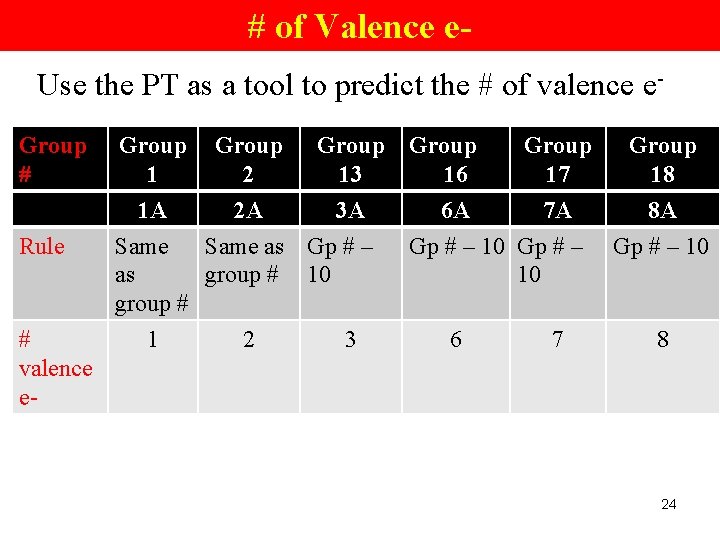
# of Valence e. Use the PT as a tool to predict the # of valence e. Group # Group 1 Rule 1 A 2 A 3 A Same as Gp # – as group # 10 group # # valence e- 1 Group 2 2 Group 13 3 Group 16 Group 17 6 A 7 A Gp # – 10 6 7 Group 18 8 A Gp # – 10 8 24

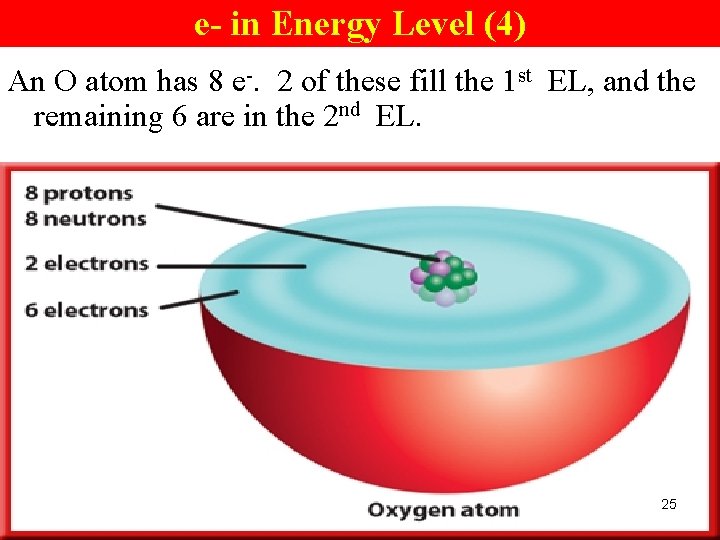
e- in Energy Level (4) An O atom has 8 e-. 2 of these fill the 1 st EL, and the remaining 6 are in the 2 nd EL. 25

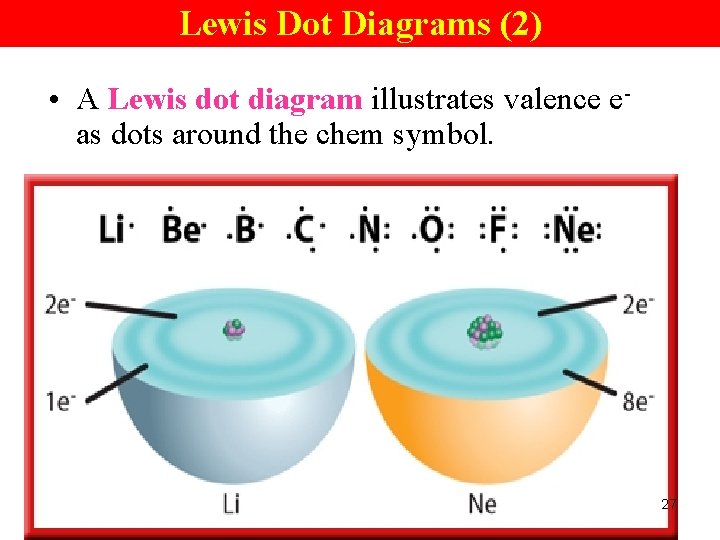
Lewis Dot Diagrams (1) • Because valence e- are so important to the behavior of an atom, it is useful to represent them with symbols. 26

Lewis Dot Diagrams (2) • A Lewis dot diagram illustrates valence eas dots around the chem symbol. 27

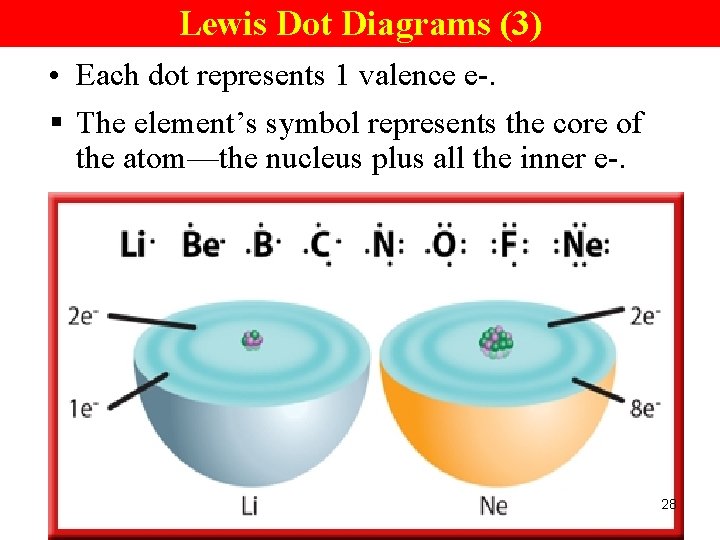
Lewis Dot Diagrams (3) • Each dot represents 1 valence e-. § The element’s symbol represents the core of the atom—the nucleus plus all the inner e-. 28

Quantum Mechanical Model The quantum mechanical model determines the allowed energies an e- can have and how likely it is to find the e- in various locations around the nucleus. 29

Atomic Orbitals An atomic orbital is often thought of as a region of space in which there is a high probability of finding an e-. Each energy sublevel corresponds to an orbital of a different shape, which describes where the eis likely to be found. 30

CST Problem 1 When a metal is heated in a flame, the flame has distinctive color. This information was eventually extended to the study of stars because A the color spectra of stars indicate which elements are present B a red shift in star color indicates stars are moving away. C star color indicates absolute distance. D it allows the observer to determine the size of stars. 31

CST Example 2 Which statement best describe the density of an atom’s nucleus? A the nucleus occupies most of the atom’s volume but contains little of its mass. B the nucleus occupies very little of the atom’s volume and contains little of its mass. C the nucleus occupies most of the atom’s volume and contains most of its mass. D The nucleus occupies very little of the atom’s volume but contains most of its mass. 32

The End 33