Chapter 5 Dynamic Behavior In analyzing process dynamic

Chapter 5 Dynamic Behavior In analyzing process dynamic and process control systems, it is important to know how the process responds to changes in the process inputs. A number of standard types of input changes are widely used for two reasons: 1. They are representative of the types of changes that occur in plants. 2. They are easy to analyze mathematically.
Chapter 5

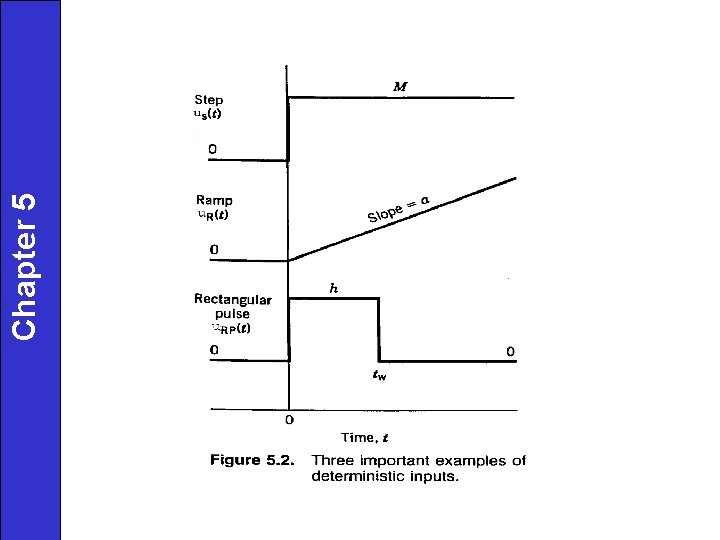
Step Input Chapter 5 A sudden change in a process variable can be approximated by a step change of magnitude, M: The step change occurs at an arbitrary time denoted as t = 0. • Special Case: If M = 1, we have a “unit step change”. We give it the symbol, S(t). • Example of a step change: A reactor feedstock is suddenly switched from one supply to another, causing sudden changes in feed concentration, flow, etc.

Chapter 5 Example: The heat input to the stirred-tank heating system in Chapter 2 is suddenly changed from 8000 to 10, 000 kcal/hr by changing the electrical signal to the heater. Thus,
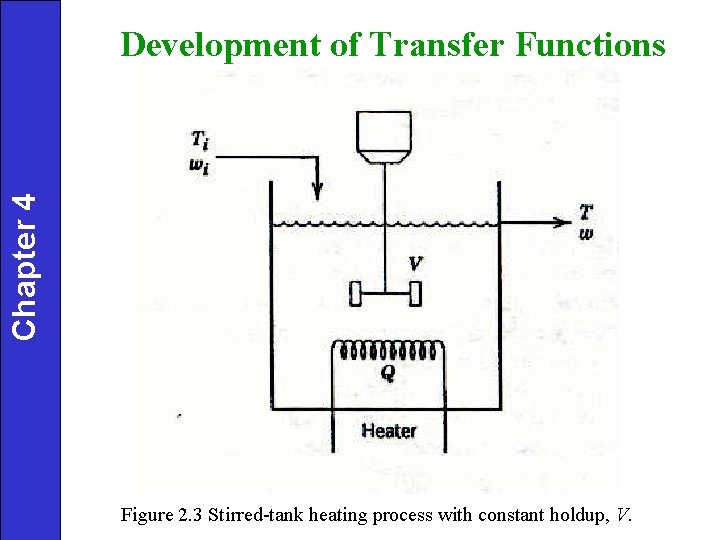
Chapter 4 Development of Transfer Functions Figure 2. 3 Stirred-tank heating process with constant holdup, V.

Chapter 4 Rearrange (5) to solve for where

Step Response of 1 st-Order System

Ramp Input • Industrial processes often experience “drifting disturbances”, that is, relatively slow changes up or down for some period of time. • The rate of change is approximately constant.

Chapter 5 We can approximate a drifting disturbance by a ramp input: Examples of ramp changes: 1. Ramp a setpoint to a new value. (Why not make a step change? ) 2. Feed composition, heat exchanger fouling, catalyst activity, ambient temperature.

Ramp Response of 1 st-Order System
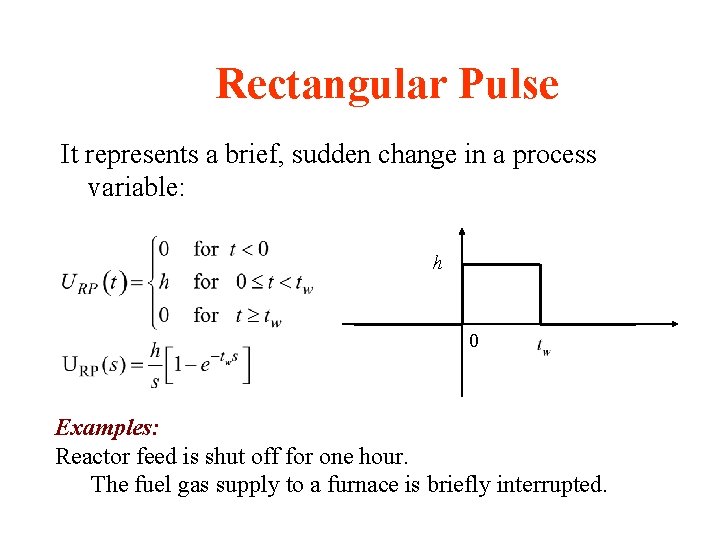
Rectangular Pulse It represents a brief, sudden change in a process variable: h 0 Examples: Reactor feed is shut off for one hour. The fuel gas supply to a furnace is briefly interrupted.

Response of 1 st-Order System to Rectangular Pulse

Impulse Input • It represents a short, transient disturbance. • It is the limit of a rectangular pulse for tw→ 0 and h = 1/tw Examples: Electrical noise spike in a thermo-couple reading. Injection of a tracer dye.

Impulse Response of 1 st-Order System

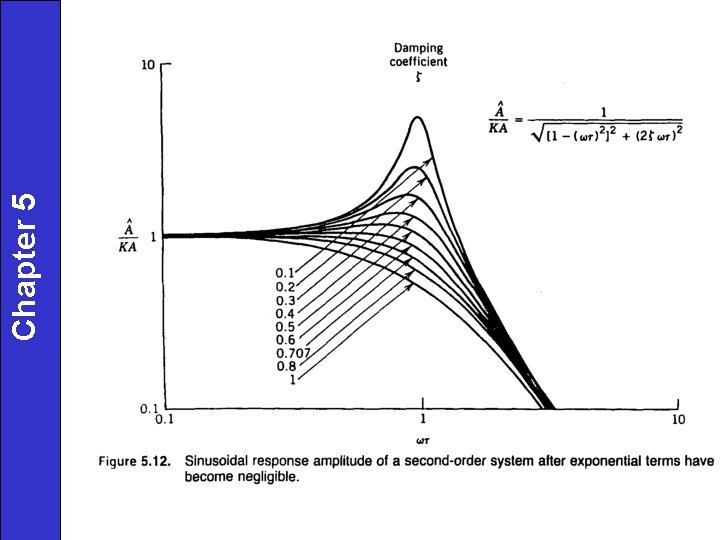
Chapter 5 Sinusoidal Input

Chapter 5 Processes are also subject to periodic, or cyclic, disturbances. They can be approximated by a sinusoidal disturbance: where: A = amplitude, ω = angular frequency Examples: 1. 24 hour variations in cooling water temperature. 2. 60 -Hz electrical noise (in USA!)

For a sine input to the 1 st order process: Chapter 5 output is. . . By partial fraction decomposition,

this term dies out for large t Chapter 5 Inverting, Note that the amplitude ration and phase angle is not a function of t but of t and w. For large t, y(t) is also sinusoidal, output sine is attenuated by…

Example of 2 nd Order Process Non-Interacting Storage System
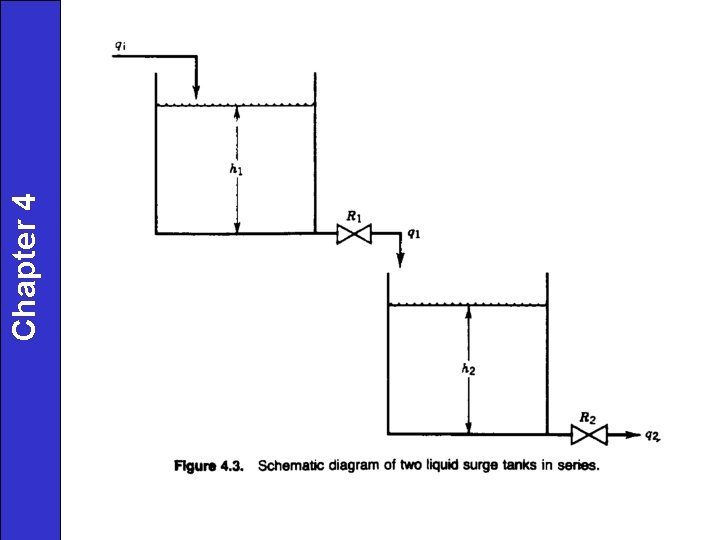
Chapter 4
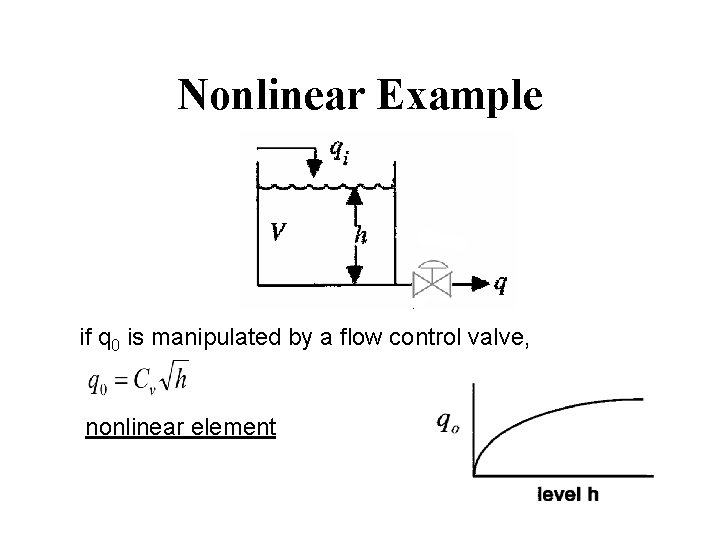
Nonlinear Example if q 0 is manipulated by a flow control valve, nonlinear element
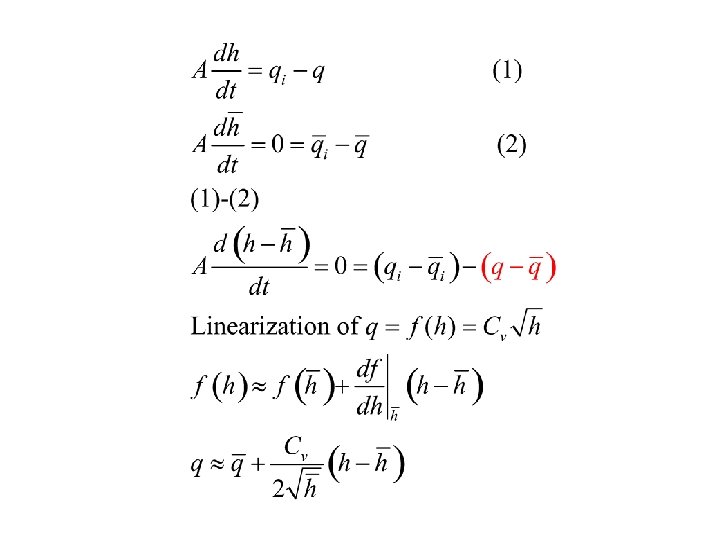

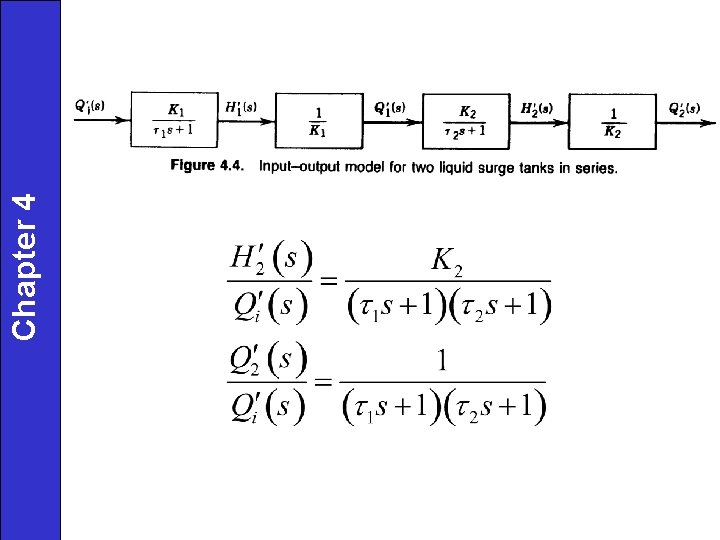
Chapter 4

Example of 2 nd Order Process Interacting Storage System
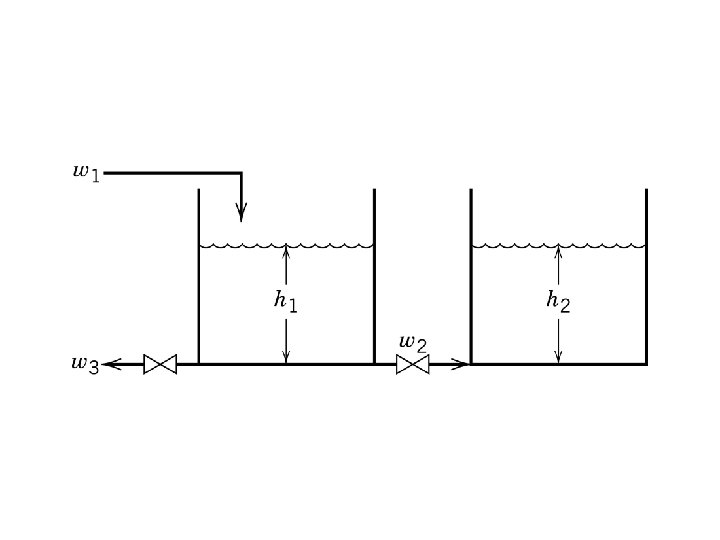

Example 4. 2 Interacting Electrically Heated Stirred Tank System
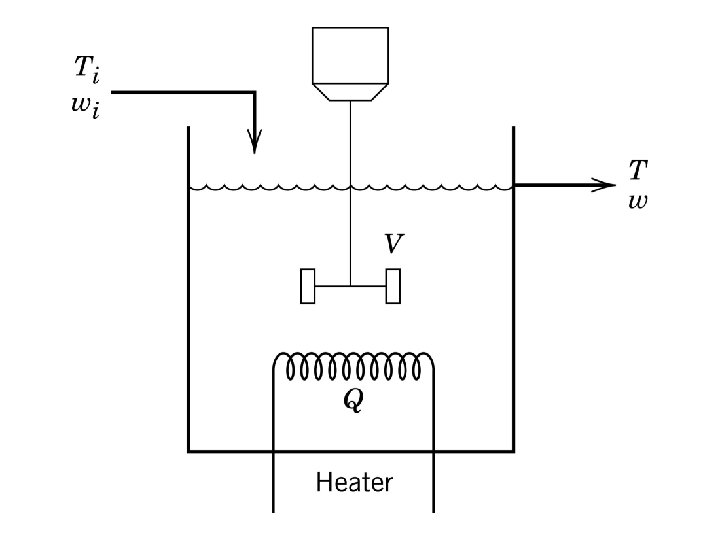

Dynamical Model and Transfer Functions

Chapter 5 Note that, when Ce 0, we obtain 1 st order equation (simpler model)

Standard Form of 2 nd Order Transfer Function

Characteristic Equation

Solutions of 2 nd Order Linear ODE

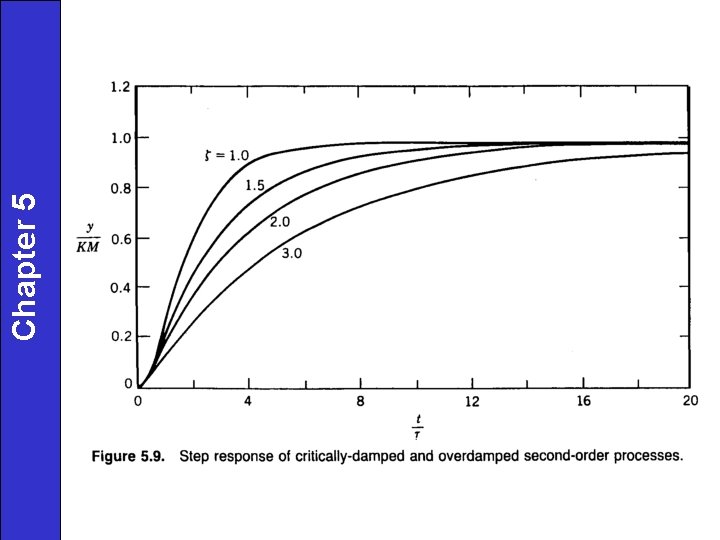
Step Response of 2 nd-Order Overdamped System
Chapter 5

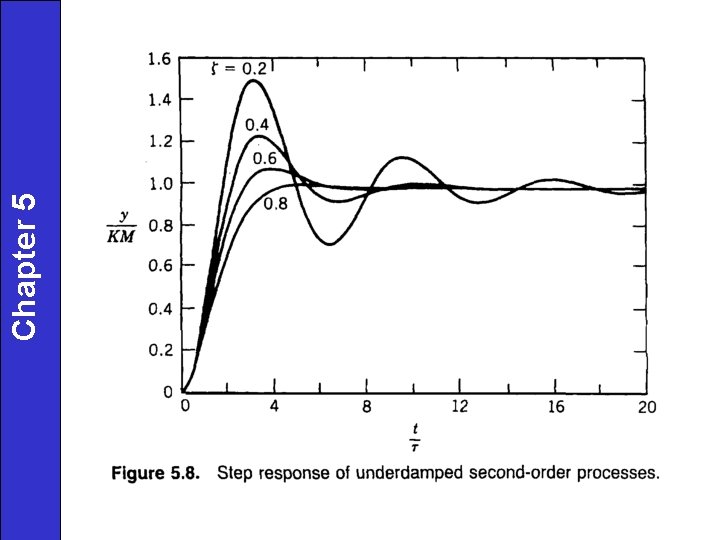
Step Response of 2 nd-Order Underdamped System
Chapter 5
Chapter 5 1

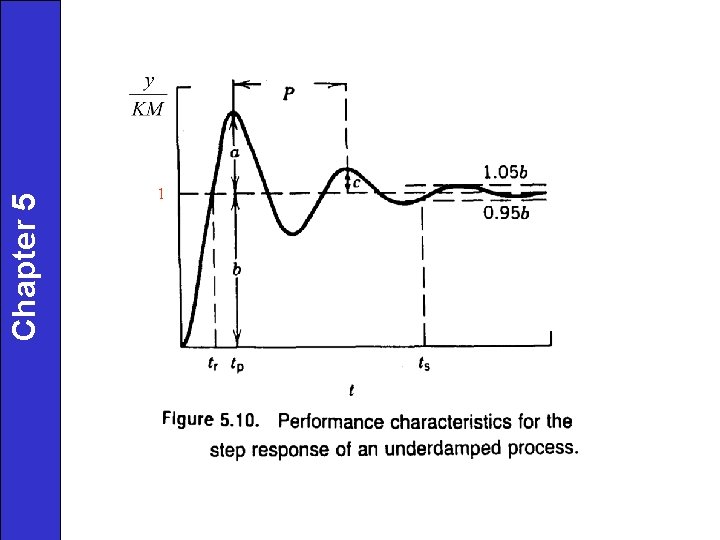
Rise Time

Peak Time

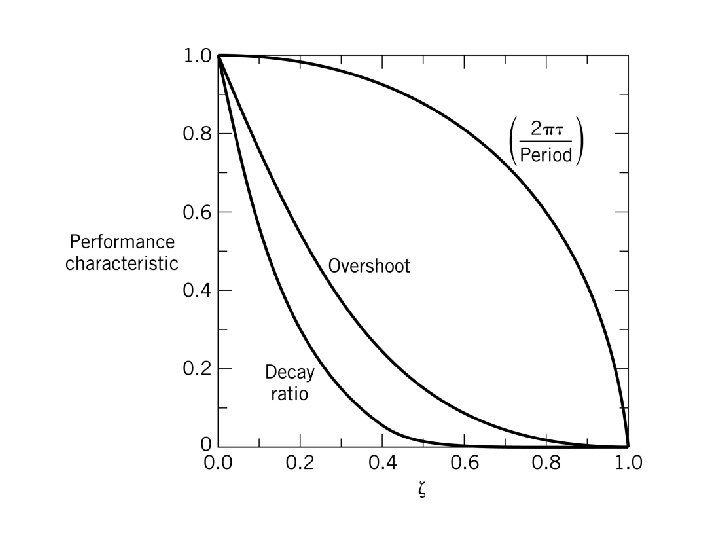
Maximum Overshoot Ratio

Decay Ratio

Second Order Step Change Chapter 5 a. Overshoot b. time of first maximum c. decay ratio (successive maxima – not min. ) d. period of oscillation
Chapter 5
- Slides: 45