Chapter 5 Discrete Probability Distributions 2002 Thomson SouthWestern

Learning Objectives • Distinguish between discrete random variables and continuous random variables. • Identify the type of statistical experiments that can be described by the binomial distribution, and know how to work such problems. © 2002 Thomson / South-Western 2

Learning Objectives, continued • Decide when to use the Poisson distribution in analyzing statistical experiments, and know how to work such problems. • Decide when to use the hypergeometric distribution, and know how to work such problems. © 2002 Thomson / South-Western 3

Discrete vs Continuous Distributions • Random Variable -- a variable which contains the outcomes of a chance experiment • Discrete Random Variable -- the set of all possible values is at most a finite or a countable infinite number of possible values • Continuous Random Variable -- takes on values at every point over a given interval © 2002 Thomson / South-Western 4

Some Special Distributions • Discrete distributions are constructed from discrete ransom variables. • The binomial, Poisson, and hypergeometric distributions are discrete distributions • Continuous distributions are based on continuous random variables. • The normal, uniform, exponential, t, chisquare, and F distributions are continuous distributions © 2002 Thomson / South-Western 5

Binomial Distribution A widely known discrete distribution constructed by determining the probabilities of X

Assumptions of the Binomial Distribution • The experiment involves n identical trials • Each trial has only two possible outcomes: success and failure • Each trial is independent of the previous trials • The terms p and q remain constant throughout the experiment – p is the probability of a success on any one trial – q = (1 -p) is the probability of a failure on any one trial © 2002 Thomson / South-Western 7

Assumptions of the Binomial Distribution, continued • In the n trials X is the number of successes possible where X is a whole number between 0 and n. • Applications – Sampling with replacement – Sampling without replacement causes p to change but if the sample size n < 5% N, the independence assumption is not a great concern. © 2002 Thomson / South-Western 8

Binomial Distribution: Development • Experiment: randomly select, with replacement, two families from the residents of the four-family town • Success is ‘Children in Household: ’ p = 0. 75 • Failure is ‘No Children in Household: ’ q = 1 - p = 0. 25 • X is the number of families in the sample with ‘Children in Household’ © 2002 Thomson / South-Western 9

Binomial Distribution: Development continued (2) Family A B C D Children in Household Number of Automobiles Yes No Yes 3 2 1 2 © 2002 Thomson / South-Western Listing of Sample Space (A, B), (A, C), (A, D), (D, D), (B, A), (B, B), (B, C), (B, D), (C, A), (C, B), (C, C), (C, D), (D, A), (D, B), (D, C), (D, D) 10

Binomial Distribution: Development continued (3) • Families A, B, and D have children in the household; family C does not • Success is ‘Children in Household: ’ p = 0. 75 • Failure is ‘No Children in Household: ’ q = 1 - p = 0. 25 • X is the number of families in the sample with ‘Children in Household’ © 2002 Thomson / South-Western Listing of Sample Space P(outcome) (A, B), (A, C), (A, D), (D, D), (B, A), (B, B), (B, C), (B, D), (C, A), (C, B), (C, C), (C, D), (D, A), (D, B), (D, C), (D, D) 1/16 1/16 1/16 1/16 X 2 1 2 1 1 0 1 2 2 11

Binomial Distribution: Development continued (4) Listing of Sample Space P(outcome) (A, B), (A, C), (A, D), (D, D), (B, A), (B, B), (B, C), (B, D), (C, A), (C, B), (C, C), (C, D), (D, A), (D, B), (D, C), (D, D) 1/16 1/16 1/16 1/16 © 2002 Thomson / South-Western X 2 1 2 1 1 0 1 2 2 1 2 X 0 1 2 P(X) 1/16 6/16 9/16 1 12

Binomial Distribution: Development continued (5) • Families A, B, and D have children in the household; family C does not • Success is Children in Household: p = 0. 75 • Failure is No Children in Household, q = 1 p = 0. 25 • X is the number of families in the sample with Children in Household © 2002 Thomson / South-Western Possible Sequences P(sequence) (F, F) (. 25)2 0 (S, F) (. 75)(. 25) 1 (F, S) (. 25)(. 75) 1 (S, S) (. 75)2 2 X 13

Binomial Distribution: Development continued (6) Possible Sequences P(sequence) (F, F) X X (. 25)2 0 0 (S, F) (. 75)(. 25) 1 1 (F, S) (. 25)(. 75) 1 2 (S, S) (. 75)2 2 © 2002 Thomson / South-Western P(X) (. 25)2 =0. 0625 2 (. 25)(. 75) =0. 375 (. 75)2 =0. 5625 14

Binomial Distribution: Demonstration Problem 5. 2 © 2002 Thomson / South-Western 15

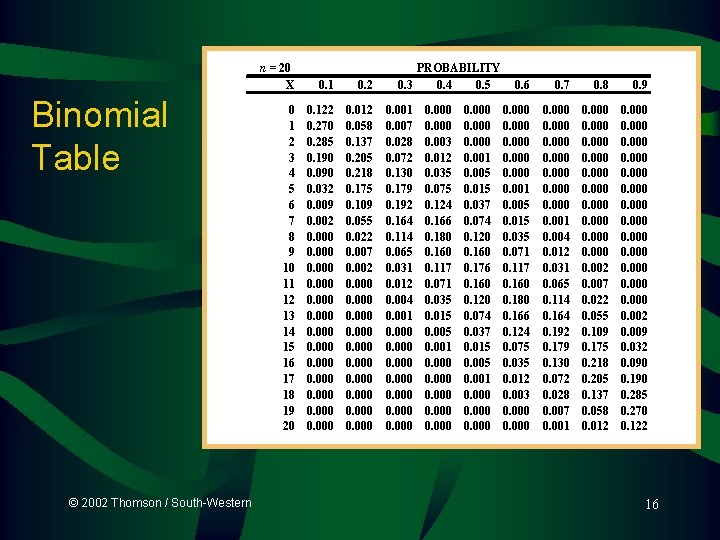
Binomial Table © 2002 Thomson / South-Western n = 20 X 0. 1 0. 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 0. 122 0. 270 0. 285 0. 190 0. 032 0. 009 0. 002 0. 000 0. 012 0. 058 0. 137 0. 205 0. 218 0. 175 0. 109 0. 055 0. 022 0. 007 0. 002 0. 000 0. 000 PROBABILITY 0. 3 0. 4 0. 5 0. 001 0. 007 0. 028 0. 072 0. 130 0. 179 0. 192 0. 164 0. 114 0. 065 0. 031 0. 012 0. 004 0. 001 0. 000 0. 003 0. 012 0. 035 0. 075 0. 124 0. 166 0. 180 0. 160 0. 117 0. 071 0. 035 0. 015 0. 001 0. 000 0. 001 0. 005 0. 015 0. 037 0. 074 0. 120 0. 160 0. 176 0. 160 0. 120 0. 074 0. 037 0. 015 0. 001 0. 000 0. 6 0. 7 0. 8 0. 9 0. 000 0. 001 0. 005 0. 015 0. 035 0. 071 0. 117 0. 160 0. 180 0. 166 0. 124 0. 075 0. 035 0. 012 0. 003 0. 000 0. 001 0. 004 0. 012 0. 031 0. 065 0. 114 0. 164 0. 192 0. 179 0. 130 0. 072 0. 028 0. 007 0. 001 0. 000 0. 002 0. 007 0. 022 0. 055 0. 109 0. 175 0. 218 0. 205 0. 137 0. 058 0. 012 0. 000 0. 002 0. 009 0. 032 0. 090 0. 190 0. 285 0. 270 0. 122 16

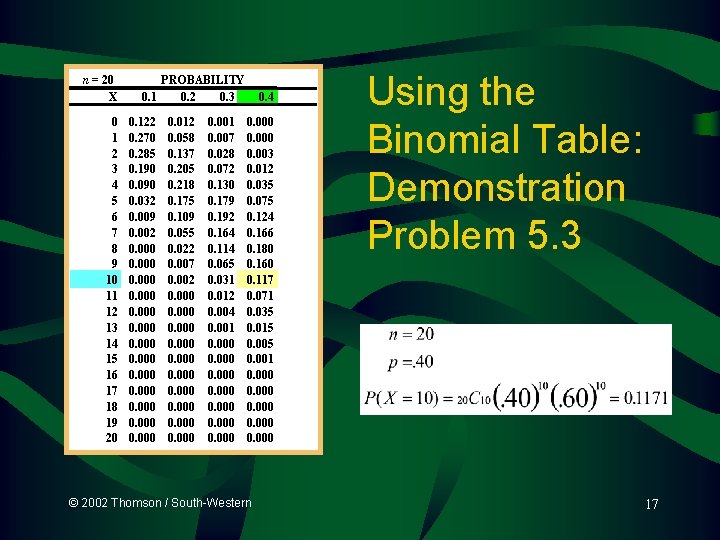
n = 20 X 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 PROBABILITY 0. 1 0. 2 0. 3 0. 122 0. 270 0. 285 0. 190 0. 032 0. 009 0. 002 0. 000 0. 012 0. 058 0. 137 0. 205 0. 218 0. 175 0. 109 0. 055 0. 022 0. 007 0. 002 0. 000 0. 001 0. 007 0. 028 0. 072 0. 130 0. 179 0. 192 0. 164 0. 114 0. 065 0. 031 0. 012 0. 004 0. 001 0. 000 0. 4 0. 000 0. 003 0. 012 0. 035 0. 075 0. 124 0. 166 0. 180 0. 160 0. 117 0. 071 0. 035 0. 015 0. 001 0. 000 © 2002 Thomson / South-Western Using the Binomial Table: Demonstration Problem 5. 3 17

Binomial Distribution • Probability function • Mean value • Variance and standard deviation ©

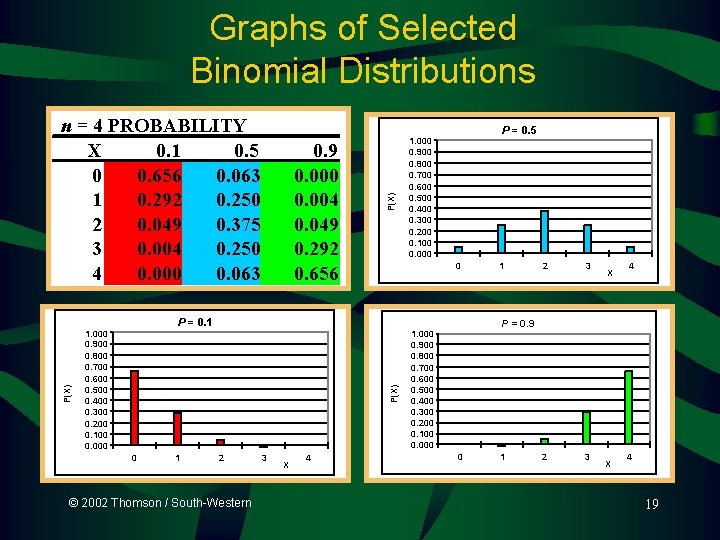
n = 4 PROBABILITY X 0. 1 0. 5 0 0. 656 0. 063 1 0. 292 0. 250 2 0. 049 0. 375 3 0. 004 0. 250 4 0. 000 0. 063 0. 9 0. 000 0. 004 0. 049 0. 292 0. 656 P(X) Graphs of Selected Binomial Distributions P = 0. 5 1. 000 0. 900 0. 800 0. 700 0. 600 0. 500 0. 400 0. 300 0. 200 0. 100 0. 000 0 P(X) P = 0. 1 1. 000 0. 900 0. 800 0. 700 0. 600 0. 500 0. 400 0. 300 0. 200 0. 100 0. 000 0 1 2 © 2002 Thomson / South-Western 3 X 4 1 2 3 X 4 P = 0. 9 1. 000 0. 900 0. 800 0. 700 0. 600 0. 500 0. 400 0. 300 0. 200 0. 100 0. 000 0 1 X 4 19

Assumptions of the Poisson Distribution • Describes discrete occurrences over a continuum or interval • A discrete distribution • Describes rare events • Each occurrence is independent any other occurrences. • The number of occurrences in each interval can vary from zero to infinity. • The expected number of occurrences must hold constant throughout the experiment. © 2002 Thomson / South-Western 20

Poisson Distribution • Probability function n Mean value n Variance © 2002 Thomson /

Poisson Distribution: Demonstration Problem 5. 7 © 2002 Thomson / South-Western 22

Poisson Distribution: Probability Table X 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0. 5 0. 6065 0. 3033 0. 0758 0. 0126 0. 0016 0. 0002 0. 0000 0. 0000 1. 5 0. 2231 0. 3347 0. 2510 0. 1255 0. 0471 0. 0141 0. 0035 0. 0008 0. 0001 0. 0000 0. 0000 © 2002 Thomson / South-Western 1. 6 0. 2019 0. 3230 0. 2584 0. 1378 0. 0551 0. 0176 0. 0047 0. 0011 0. 0002 0. 0000 0. 0000 3. 0 0. 0498 0. 1494 0. 2240 0. 1680 0. 1008 0. 0504 0. 0216 0. 0081 0. 0027 0. 0008 0. 0002 0. 0001 0. 0000 3. 2 0. 0408 0. 1304 0. 2087 0. 2226 0. 1781 0. 1140 0. 0608 0. 0278 0. 0111 0. 0040 0. 0013 0. 0004 0. 0001 0. 0000 6. 4 0. 0017 0. 0106 0. 0340 0. 0726 0. 1162 0. 1487 0. 1586 0. 1450 0. 1160 0. 0825 0. 0528 0. 0307 0. 0164 0. 0081 0. 0037 0. 0016 0. 0002 0. 0001 6. 5 0. 0015 0. 0098 0. 0318 0. 0688 0. 1118 0. 1454 0. 1575 0. 1462 0. 1188 0. 0858 0. 0558 0. 0330 0. 0179 0. 0089 0. 0041 0. 0018 0. 0007 0. 0003 0. 0001 7. 0 0. 0009 0. 0064 0. 0223 0. 0521 0. 0912 0. 1277 0. 1490 0. 1304 0. 1014 0. 0710 0. 0452 0. 0263 0. 0142 0. 0071 0. 0033 0. 0014 0. 0006 0. 0002 8. 0 0. 0003 0. 0027 0. 0107 0. 0286 0. 0573 0. 0916 0. 1221 0. 1396 0. 1241 0. 0993 0. 0722 0. 0481 0. 0296 0. 0169 0. 0090 0. 0045 0. 0021 0. 0009 23

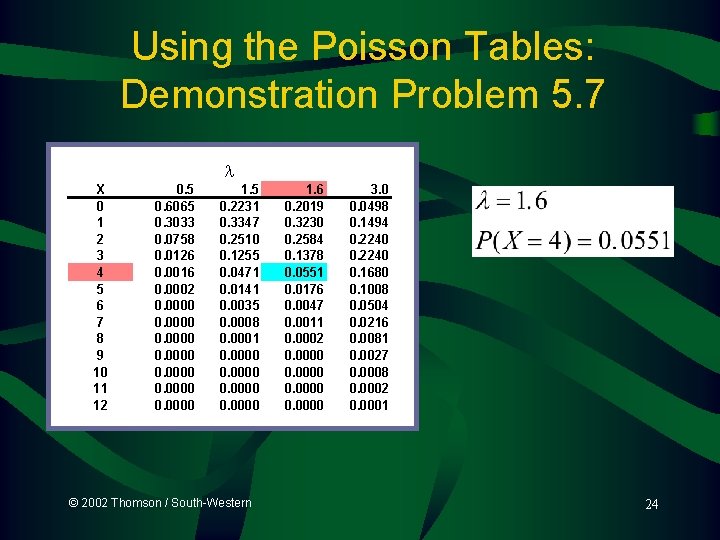
Using the Poisson Tables: Demonstration Problem 5. 7 X 0 1 2 3 4 5 6 7 8 9 10 11 12 0. 5 0. 6065 0. 3033 0. 0758 0. 0126 0. 0016 0. 0002 0. 0000 0. 0000 1. 5 0. 2231 0. 3347 0. 2510 0. 1255 0. 0471 0. 0141 0. 0035 0. 0008 0. 0001 0. 0000 © 2002 Thomson / South-Western 1. 6 0. 2019 0. 3230 0. 2584 0. 1378 0. 0551 0. 0176 0. 0047 0. 0011 0. 0002 0. 0000 3. 0 0. 0498 0. 1494 0. 2240 0. 1680 0. 1008 0. 0504 0. 0216 0. 0081 0. 0027 0. 0008 0. 0002 0. 0001 24

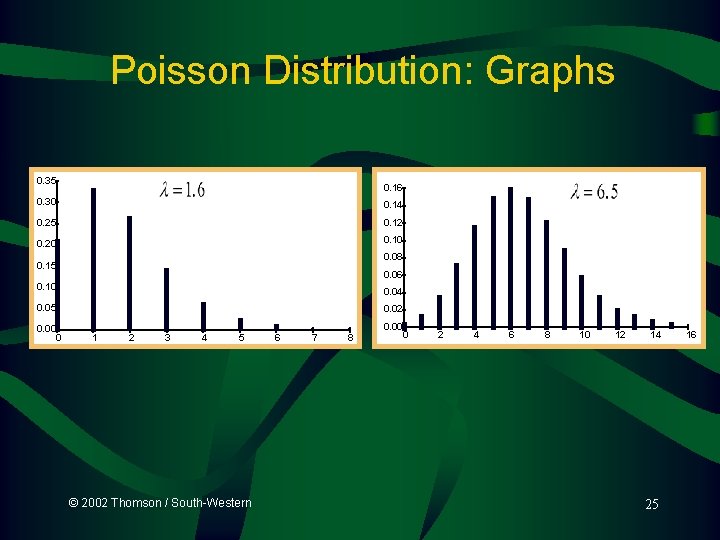
Poisson Distribution: Graphs 0. 35 0. 16 0. 30 0. 14 0. 25 0. 12 0. 20 0. 10 0. 08 0. 15 0. 06 0. 10 0. 04 0. 05 0. 00 0 0. 02 1 2 3 4 5 © 2002 Thomson / South-Western 6 7 8 0. 00 0 2 4 6 8 10 12 14 25 16

Assumptions of the Hypergeometric Distribution • It is a discrete distribution. • Sampling is done without replacement. • The number of objects in the population, N, is finite and known. • Each trial has exactly two possible outcomes: success and failure. • Trials are not independent • X is the number of successes in the n trials © 2002 Thomson / South-Western 26

Hypergeometric Distribution • Probability function – N is population size – n is sample size – A is number of successes in population – x is number of successes in sample • Mean value • Variance and standard deviation © 2002 Thomson / South-Western 27

Hypergeometric Distribution: Probability Computations N = 24 X=8 n=5 x P(x) 0 0. 1028

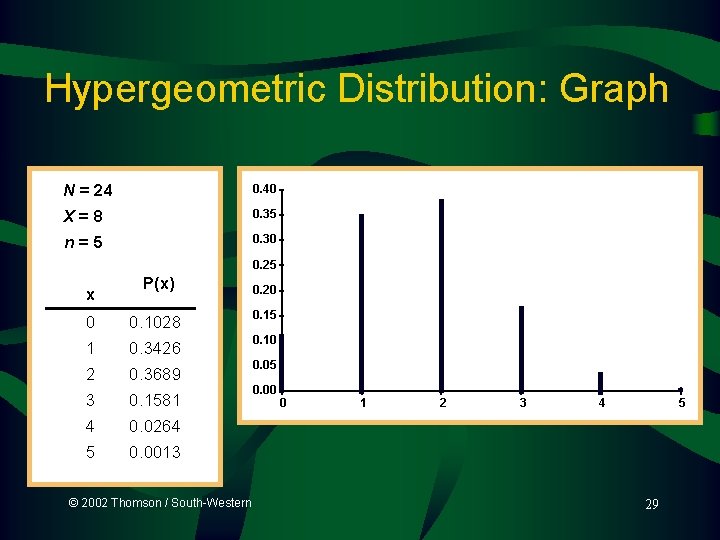
Hypergeometric Distribution: Graph N = 24 0. 40 X=8 0. 35 n=5 0. 30 0. 25 x P(x) 0. 20 0 0. 1028 0. 15 1 0. 3426 0. 10 2 0. 3689 3 0. 1581 4 0. 0264 5 0. 0013 © 2002 Thomson / South-Western 0. 05 0. 00 0 1 2 3 4 5 29

Hypergeometric Distributio: Demonstration Problem 5. 8 N = 18 n=3 A = 12 ©

The Hypergeometric Distribution and the Binomial Distribution • Because the hypergeometric distribution is described by three parameters N, A and n, it is practically impossible to create tables for easy use. • The binomial (which has tables) is an acceptable approximation, if n < 5% N. Otherwise it is not. • Excel has eliminated all the tedious calculations and allows the user to compute the exact probabilities for the hypergeometric. © 2002 Thomson / South-Western 31