Chapter 5 Data representation Aim Explain how integers

Chapter 5 Data representation

Aim • Explain how integers are represented in computers using: • Explain how fractional numbers are represented in computers • Calculate the decimal value represented by a binary sequence in: • Explain how characters are represented in computers • Explain how colours, images, sound and movies are represented • • Unsigned, signed magnitude, excess, and two’s complement notations Floating point notation (IEEE 754 single format) Unsigned, signed notation, excess, two’s complement, and the IEEE 754 notations. E. g. using ASCII and Unicode

Integer Representations • Unsigned notation • Signed magnitude notion • Excess notation • Two’s complement notation.

Unsigned Representation Represents positive integers. Unsigned representation of 157: position Bit pattern contribution 7 6 1 0 27 Addition is simple: 5 4 0 1 1 24 23 1 0 0 1 + 0 1 = 1 1 1 0. 3 2 1 0 1 22 0 1 20

Advantages and disadvantages of unsigned notation Advantages: Disadvantages • One representation of zero • Simple addition • Negative numbers can not be represented. • The need of different notation to represent negative numbers.

Signed Magnitude Representation In signed magnitude the left most bit represents the sign of the integer. • 0 for positive numbers. • 1 for negative numbers. The remaining bits represent to magnitude of the numbers.

Example Suppose 10011101 is a signed magnitude representation. The sign bit is 1, then the number represented is negative position 7 6 5 4 3 2 1 0 Bit pattern 1 0 0 1 1 1 0 1 contribution 24 23 22 20 The magnitude is 0011101 with a value 24+23+22+20= 29

Exercise 1 1. 3710 has 0010 0101 in signed magnitude notation. Find the signed magnitude of – 3710 ? 2. Using the signed magnitude notation find the 8 -bit binary representation of the decimal value 2410 and -2410. 3. Find the signed magnitude of – 63 using 8 -bit binary sequence?

Signed-Summary In signed magnitude notation, • the most significant bit is used to represent the sign. • 1 represents negative numbers • 0 represents positive numbers. • The unsigned value of the remaining bits represent The magnitude. Advantages: • Represents positive and negative numbers Disadvantages: • • two representations of zero, difficult operation.

Excess Notation In excess notation: • the value represented is the unsigned value with a fixed value subtracted from it. • • For n-bit binary sequences the value subtracted fixed value is 2(n-1). Most significant bit: • • 0 for negative numbers 1 for positive numbers

Excess Notation with n bits 1000… 0 represent 2 n-1 is the decimal value in unsigned notation. Decimal value In unsigned notation - 2 n-1 = Decimal value In excess notation Therefore, in excess notation: • 1000… 0 will represent 0.

Example (1) - excess to decimal Find the decimal number represented by 1001 in excess notation. • Unsigned value • 100110002 = 27 + 24 + 23 + 20 = 128 + 16 +8 +1 = 15310 • excess value = 153 – 27 = 152 – 128 = 25. • Excess value:

Example (2) - decimal to excess Represent the decimal value 24 in 8 -bit excess notation. We first add, 28 -1, the fixed value then, find the unsigned value of 152 • 24 + 28 -1 = 24 + 128= 152 • 15210 = 10011000 (unsigned notation). • 2410 = 10011000 (excess notation)

example (3) Represent the decimal value -24 in 8 -bit excess notation. We first add, 28 -1, the fixed value then, find the unsigned value of 104 • -24 + 28 -1 = -24 + 128= 104 • • 10410 = 01101000 (unsigned notation). -2410 = 01101000 (excess notation)

Example (4) -- 10101 Unsigned • • 101012 = 16+4+1 = 2110 The value represented in unsigned notation is 21 Sign Magnitude • • • The sign bit is 1, so the sign is negative The magnitude is the unsigned value 01012 = 510 So the value represented in signed magnitude is -510 Excess notation • • • As an unsigned binary integer 101012 = 2110 subtracting 25 -1 = 16, we get 21 -16 = 510. So the value represented in excess notation is 510.

Excess notation - Summary In excess notation, the value represented is the unsigned value with a fixed value subtracted from it. • i. e. for n-bit binary sequences the value subtracted is 2(n-1). Most significant bit: • • 0 for negative numbers. 1 positive numbers. Advantages: • • Only one representation of zero. Easy for comparison.

Two’s Complement Notation The most used representation for integers. • All positive numbers begin with 0. • All negative numbers begin with 1. • One representation of zero • i. e. 0 is represented as 0000 using 4 -bit binary sequence.

Properties of Two’s Complement Notation Positive numbers begin with 0 Negative numbers begin with 1 Only one representation of 0, i. e. 0000 Relationship between +n and –n. • 0 1 0 0 +4 0 0 0 1 0 +18 • 1 1 0 0 -4 1 1 1 0 -18

Two’s complement-summary In two’s complement the most significant for an n-bit number has a contribution of – 2(n-1). One representation of zero All arithmetic operations can be performed by using addition and inversion. The most significant bit: 0 for positive and 1 for negative. Three methods can the decimal value of a negative number: Method 1 decimal value of (n-1) bits, then subtract 2 n-1 Method 2 - 2 n-1 is the contribution of the sign bit. Method 3 • Binary rep. of the corresponding positive number. • Let V be its decimal value. • - V is the required value.

Exercise - 10001011 Determine the decimal value represented by 10001011 in each of the following four systems. 1. Unsigned notation? 2. Signed magnitude notation? 3. Excess notation? 4. Tow’s complements?

Fraction Representation • Floating point representation.

Floating Point Representation format Sign Exponent Mantissa The exponent is biased by a fixed value b, called the bias. The mantissa should be normalised, e. g. if the real mantissa if of the form 1. f then the normalised mantissa should be f, where f is a binary sequence.

Representation in IEEE 754 single precision sign bit: 8 biased exponent by 127 23 bit normalised mantissa • 0 for positive and, • 1 for negative numbers Sign Exponent Mantissa

Example (1) 5. 7510 in IEEE single precision 5. 75 is a positive number then the sign bit is 0. 5. 75 = 101. 11 * 20 = 10. 111 * 21 = 1. 0111 * 22 The real mantissa is 1. 0111, then the normalised mantissa is 0111 0000 000 The real exponent is 2 and the bias is 127, then the exponent is 2 + 127=12910 = 1000 00012. The representation of 5. 75 in IEE sing-precision is: 0 1000 0001 0111 0000 000

Example (2) which number does the following IEEE single precision notation represent? 1 1000 0100 0000 000 The sign bit is 1, hence it is a negative number. The exponent is 1000 0000 = 12810 It is biased by 127, hence the real exponent is 128 – 127 = 1. The mantissa: 0100 0000 000. It is normalised, hence the true mantissa is 1. 01 = 1. 2510 Finally, the number represented is: -1. 25 x 21 = -2. 50

Single Precision Format The exponent is formatted using excess-127 notation, with an implied base of 2 • Example: • • Exponent: 10000111 Representation: 135 – 127 = 8 The stored values 0 and 255 of the exponent are used to indicate special values, the exponential range is restricted to 2126 to 2127 The number 0. 0 is defined by a mantissa of 0 together with the special exponential value 0 The standard allows also values +/-∞ (represented as mantissa +/-0 and exponent 255 Allows various other special conditions

In comparison The smallest and largest possible 32 -bit integers in two’s complement are only -232 and 231 - 1 2021/3/4 PITT CS 1621 27

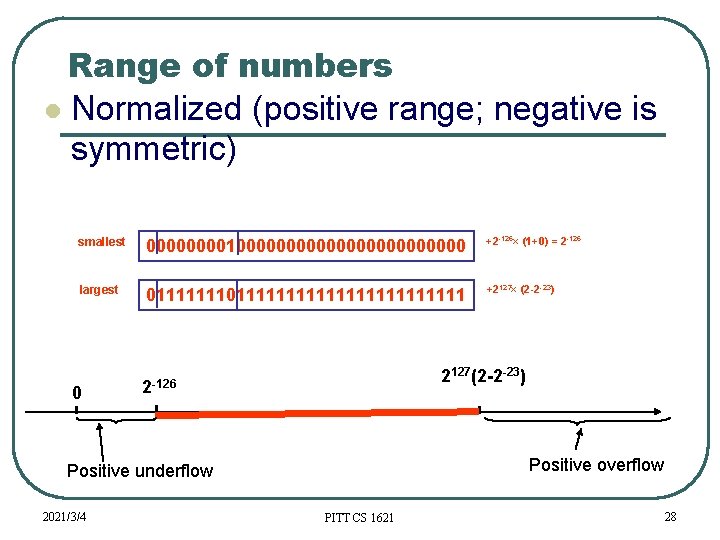
Range of numbers Normalized (positive range; negative is symmetric) smallest 00001000000000000 +2 -126× (1+0) = 2 -126 largest 0111111111111111 +2127× (2 -2 -23) 0 2127(2 -2 -23) 2 -126 Positive overflow Positive underflow 2021/3/4 PITT CS 1621 28

Representation in IEEE 754 double precision format It uses 64 bits • 1 bit sign • 11 bit exponent biased by 1023. • 52 bit mantissa Sign Exponent Mantissa

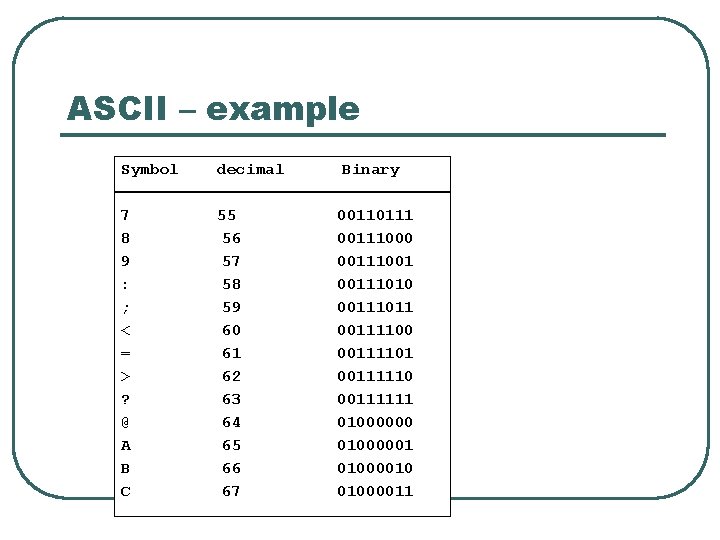
Character representation- ASCII (American Standard Code for Information Interchange) It is the scheme used to represent characters. Each character is represented using 7 -bit binary code. If 8 -bits are used, the first bit is always set to 0 See (table 5. 1 p 56, study guide) for character representation in ASCII.

ASCII – example Symbol decimal Binary 7 8 9 : ; < = > ? @ A B C 55 56 57 58 59 60 61 62 63 64 65 66 67 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 01000000 01000001 01000010 01000011

Character strings How to represent character strings? A collection of adjacent “words” (bit-string units) can store a sequence of letters 'H' 'e' 'l' o' ' ' 'W' 'o' 'r' 'l' 'd' '' Notation: enclose strings in double quotes Representation convention: null character defines end of string • "Hello world" • Null is sometimes written as '' • Its binary representation is the number 0

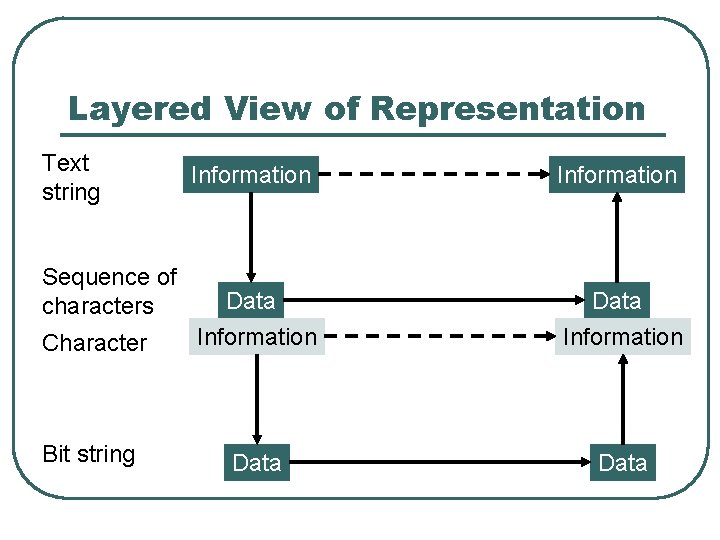
Layered View of Representation Text string Information Character Data Information Bit string Data Sequence of characters

Unicode - representation ASCII code can represent only 128 = 27 characters. It only represents the English Alphabet plus some control characters. Unicode is designed to represent the worldwide interchange. It uses 16 bits and can represents 32, 768 characters. For compatibility, the first 128 Unicode are the same as the one of the ASCII.

Colour representation Colours can represented using a sequence of bits. 256 colours – how many bits? • Hint for calculating • • To figure out how many bits are needed to represent a range of values, figure out the smallest power of 2 that is equal to or bigger than the size of the range. That is, find x for 2 x => 256 24 -bit colour – how many possible colors can be represented? • Hints • 16 million possible colours (why 16 millions? )

24 -bits -- the True colour • 24 -bit color is often referred to as the true • colour. Any real-life shade, detected by the naked eye, will be among the 16 million possible colours.

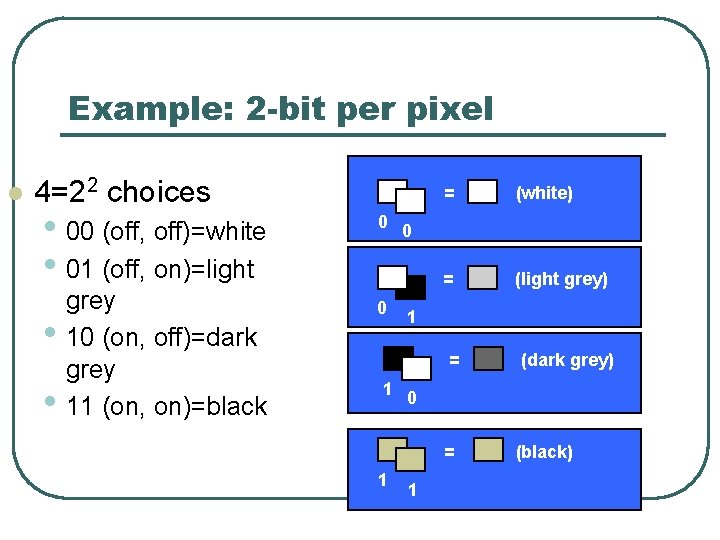
Example: 2 -bit per pixel 4=22 choices • 00 (off, off)=white • 01 (off, on)=light • • grey 10 (on, off)=dark grey 11 (on, on)=black 0 0 = (white) = (light grey) 0 1 = 1 0 = 1 (dark grey) 1 (black)

Image representation An image can be divided into many tiny squares, called pixels. Each pixel has a particular colour. The quality of the picture depends on two factors: • the density of pixels. • The length of the word representing colours. The resolution of an image is the density of pixels. The higher the resolution the more information the image contains.

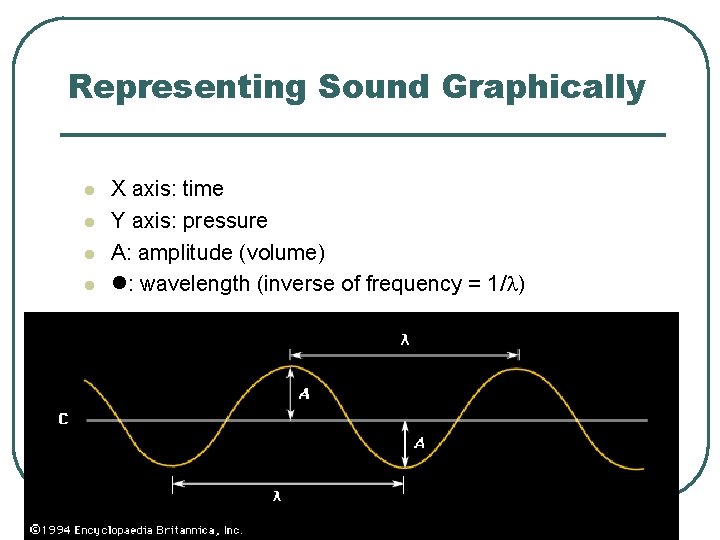
Representing Sound Graphically X axis: time Y axis: pressure A: amplitude (volume) : wavelength (inverse of frequency = 1/ )

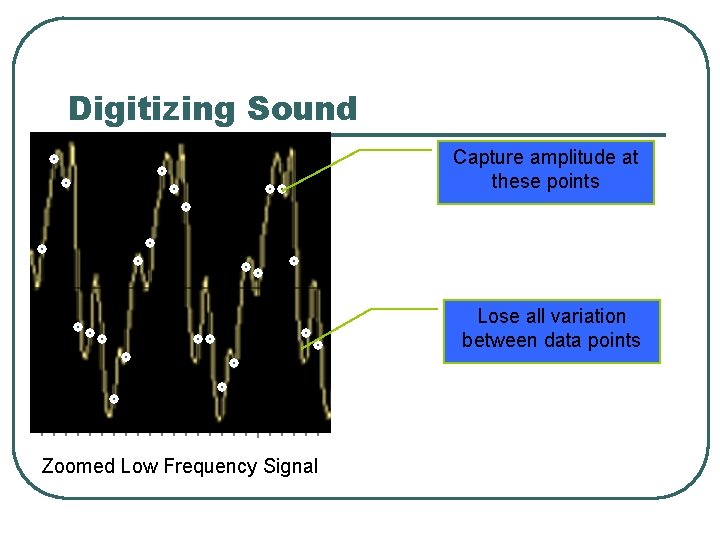
Sampling is a method used to digitise sound waves. A sample is the measurement of the amplitude at a point in time. The quality of the sound depends on: • The sampling rate, the faster the better • The size of the word used to represent a sample.

Digitizing Sound Capture amplitude at these points Lose all variation between data points Zoomed Low Frequency Signal

Summary Integer representation • • Unsigned, Signed, Excess notation, and Two’s complement. Fraction representation • Floating point (IEEE 754 format ) • Single and double precision Character representation Colour representation Sound representation