Chapter 5 Data representation 1 Learning outcomes By

Chapter 5 Data representation 1

Learning outcomes By the end of this Chapter you will be able to: • Explain how integers are represented in computers using: • Explain how fractional numbers are represented in computers • Calculate the decimal value represented by a binary sequence in: • Explain how characters are represented in computers • Explain how colours, images, sound and movies are represented • • Unsigned, signed magnitude, excess, and two’s complement notations Floating point notation (IEEE 754 single format) Unsigned, signed notation, excess, two’s complement, and the IEEE 754 notations. E. g. using ASCII and Unicode 2

Additional Reading Essential Reading Further Reading • Stalling (2003): Chapter 9 • Brookshear (2003): Chapter 1. 4 - 1. 7 • Burrell (2004): Chapter 2 • Schneider and Gersting (2004): Chapter 4. 2 3

Introduction In Chapter 3 • • in the main memory, magnetic memory, and optical memory In Chapter 4: • • How information is stored We studied how information is processed in computers How the CPU executes instructions In Chapter 5 • • • We will be looking at how data is represented in computers Integer and fractional number representation Characters, colours and sounds representation 4

Binary numbers Binary number is simply a number comprised of only 0's and 1's. Computers use binary numbers because it's easy for them to communicate using electrical current -- 0 is off, 1 is on. You can express any base 10 (our number system -- where each digit is between 0 and 9) with binary numbers. The need to translate decimal number to binary and binary to decimal. There are many ways in representing decimal number in binary numbers. (later) 5

How does the binary system work? It is just like any other system In decimal system the base is 10 In binary system the base is 2 • We have 10 possible values 0 -9 • We have only two possible values 0 or 1. • The same as in any base, 0 digit has non contribution, where 1’s has contribution which depends at there position. 6

Example 3040510 = 30000 + 400 + 5 = 3*104+4*102+5*100 101012 =10000+1 =1*24+1*22+1*20 7

Examples: decimal -- binary Find the binary representation of 12910. Find the decimal value represented by the following binary representations: • 10000011 • 1010 8

Examples: Representing fractional numbers Find the binary representations of: Using only 8 binary digits find the binary representations of: • 0. 510 = 0. 1 • 0. 7510 = 0. 11 • 0. 210 • 0. 810 9

Number representation Representing whole numbers Representing fractional numbers 10

Integer Representations • Unsigned notation • Signed magnitude notion • Excess notation • Two’s complement notation. 11

Unsigned Representation Represents positive integers. Unsigned representation of 157: position 7 6 5 4 3 2 1 0 Bit pattern 1 0 0 1 1 1 0 1 24 23 22 contribution 27 Addition is simple: 20 1 0 0 1 + 0 1 = 1 1 1 0. 12

Advantages and disadvantages of unsigned notation Advantages: Disadvantages • One representation of zero • Simple addition • Negative numbers can not be represented. • The need of different notation to represent negative numbers. 13

Representation of negative numbers Is a representation of negative numbers possible? Unfortunately: • you can not just stick a negative sign in front of a binary number. (it does not work like that) There are three methods used to represent negative numbers. • Signed magnitude notation • Excess notation • Two’s complement notation 14

Signed Magnitude Representation Unsigned: - and + are the same. In signed magnitude • the left-most bit represents the sign of the integer. • 0 for positive numbers. • 1 for negative numbers. The remaining bits represent to magnitude of the numbers. 15

Example Suppose 10011101 is a signed magnitude representation. The sign bit is 1, then the number represented is negative position 7 6 5 4 3 2 1 0 Bit pattern 1 0 0 1 1 1 0 1 24 23 22 contribution - 20 The magnitude is 0011101 with a value 24+23+22+20= 29 Then the number represented by 10011101 is – 29. 16

Exercise 1 1. 3710 has 0010 0101 in signed magnitude notation. Find the signed magnitude of – 3710 ? 2. Using the signed magnitude notation find the 8 -bit binary representation of the decimal value 2410 and -2410. 3. Find the signed magnitude of – 63 using 8 -bit binary sequence? 17

Disadvantage of Signed Magnitude Addition and subtractions are difficult. Signs and magnitude, both have to carry out the required operation. They are two representations of 0 • 0000 = + 010 • 10000000 = - 010 • To test if a number is 0 or not, • the CPU will need to see whether it is 0000 or 10000000. 0 is always performed in programs. • Therefore, having two representations of 0 is inconvenient. 18

Signed-Summary In signed magnitude notation, • The most significant bit is used to represent the sign. • 1 represents negative numbers • 0 represents positive numbers. • The unsigned value of the remaining bits represent The magnitude. Advantages: Disadvantages: • Represents positive and negative numbers • two representations of zero, • Arithmetic operations are difficult. 19

Excess Notation In excess notation: • The value represented is the unsigned value with a fixed value subtracted from it. • • For n-bit binary sequences the value subtracted fixed value is 2(n-1). Most significant bit: • • 0 for negative numbers 1 for positive numbers 20

Excess Notation with n bits 1000… 0 represent 2 n-1 is the decimal value in unsigned notation. Decimal value In unsigned notation - 2 n-1 = Decimal value In excess notation Therefore, in excess notation: • 1000… 0 will represent 0. 21

Example (1) - excess to decimal Find the decimal number represented by 1001 in excess notation. • Unsigned value • 100110002 = 27 + 24 + 23 + 20 = 128 + 16 +8 +1 = 15310 • excess value = 153 – 27 = 152 – 128 = 25. • Excess value: 22

Example (2) - decimal to excess Represent the decimal value 24 in 8 -bit excess notation. We first add, 28 -1, the fixed value then, find the unsigned value of 152 • 24 + 28 -1 = 24 + 128= 152 • 15210 = 10011000 (unsigned notation). • 2410 = 10011000 (excess notation) 23

example (3) Represent the decimal value -24 in 8 -bit excess notation. We first add, 28 -1, the fixed value then, find the unsigned value of 104 • -24 + 28 -1 = -24 + 128= 104 • • 10410 = 01101000 (unsigned notation). -2410 = 01101000 (excess notation) 24

Example (4) (10101) Unsigned • • 101012 = 16+4+1 = 2110 The value represented in unsigned notation is 21 • • • The sign bit is 1, so the sign is negative The magnitude is the unsigned value 01012 = 510 So the value represented in signed magnitude is -510 • • • As an unsigned binary integer 101012 = 2110 subtracting 25 -1 = 24 = 16, we get 21 -16 = 510. So the value represented in excess notation is 510. Sign Magnitude Excess notation 25

Advantages of Excess Notation It can represent positive and negative integers. There is only one representation for 0. It is easy to compare two numbers. When comparing the bits can be treated as unsigned integers. Excess notation is not normally used to represent integers. It is mainly used in floating point representation for representing fractions (later floating point rep. ). 26

Exercise 2 1. • • 2. Find 1001 is an 8 -bit binary sequence. Find the decimal value it represents if it was in unsigned and signed magnitude. Suppose this representation is excess notation, find the decimal value it represents? Using 8 -bit binary sequence notation, find the unsigned, signed magnitude and excess notation of the decimal value 1110 ? 27

Excess notation - Summary In excess notation, the value represented is the unsigned value with a fixed value subtracted from it. • i. e. for n-bit binary sequences the value subtracted is 2(n-1). Most significant bit: • • 0 for negative numbers. 1 positive numbers. Advantages: • • Only one representation of zero. Easy for comparison. 28

Two’s Complement Notation The most used representation for integers. • All positive numbers begin with 0. • All negative numbers begin with 1. • One representation of zero • i. e. 0 is represented as 0000 using 4 -bit binary sequence. 29

Two’s Complement Notation with 4 -bits Binary pattern 0 1 1 1 0 0 1 01 0 0 0 0 1 0 0 1 1 1 1 0 0 1 1 1 0 1 0 0 1 1 0 0 0 Value in 2’s complement. 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 -6 -7 -8 30

Properties of Two’s Complement Notation Positive numbers begin with 0 Negative numbers begin with 1 Only one representation of 0, i. e. 0000 Relationship between +n and –n. • 0100 +4 00010010 +18 • 1100 -4 1110 -18 31

Advantages of Two’s Complement Notation It is easy to add two numbers. 0 0 0 1 +1 + 0 1 +5 1 0 0 0 -8 0 +1 0 1 +5 0110 1 1 0 1 -3 +6 • Subtraction can be easily performed. • Multiplication is just a repeated addition. • Division is just a repeated subtraction • Two’s complement is widely used in ALU 32

Evaluating numbers in two’s complement notation Sign bit = 0, the number is positive. The value is determined in the usual way. Sign bit = 1, the number is negative. three methods can be used: Method 1 decimal value of (n-1) bits, then subtract 2 n-1 Method 2 - 2 n-1 is the contribution of the sign bit. Method 3 Binary rep. of the corresponding positive number. Let V be its decimal value. - V is the required value. 33

Example- 10101 in Two’s Complement The most significant bit is 1, hence it is a negative number. Method 1 • 0101 = (+5 – 25 -1 = 5 – 24 = 5 -16 = -11) Method 2 4 1 -24 +5 3 0 2 1 22 1 0 0 1 20 = -11 Method 3 • Corresponding + number is 01011 = 8 + 2+1 = 11 the result is then – 11. 34

Two’s complement-summary In two’s complement the most significant for an n-bit number has a contribution of – 2(n-1). One representation of zero All arithmetic operations can be performed by using addition and inversion. The most significant bit: 0 for positive and 1 for negative. Three methods can the decimal value of a negative number: Method 1 decimal value of (n-1) bits, then subtract 2 n-1 Method 2 - 2 n-1 is the contribution of the sign bit. Method 3 Binary rep. of the corresponding positive number. Let V be its decimal value. - V is the required value. 35

Exercise - 10001011 Determine the decimal value represented by 10001011 in each of the following four systems. 1. Unsigned notation? 2. Signed magnitude notation? 3. Excess notation? 4. Tow’s complements? 36

Fraction Representation To represent fraction we need other representations: • Fixed point representation • Floating point representation. 37

Fixed-Point Representation old position New position Bit pattern Contribution 7 6 5 4 3 2 1 0 -1 -2 -3 1 0 0 1 1. 1 0 1 24 21 20 2 -1 2 -3 =19. 625 Radix-point 38

Limitation of Fixed-Point Representation To represent large numbers or very small numbers we need a very long sequences of bits. This is because we have to give bits to both the integer part and the fraction part. 39

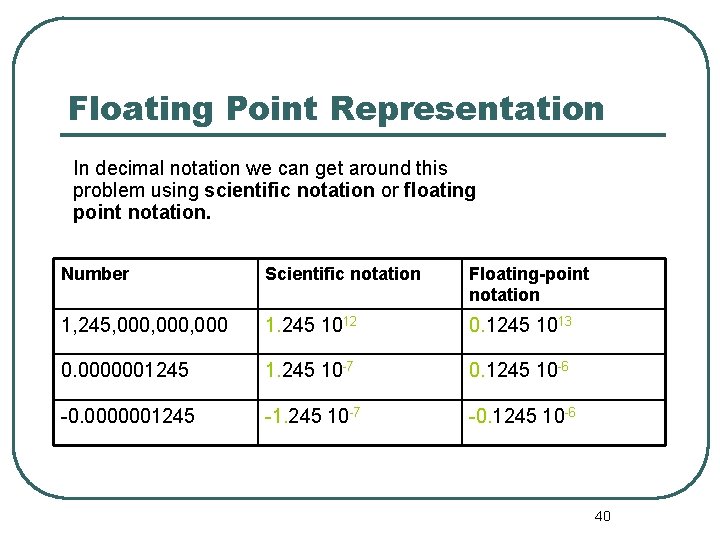
Floating Point Representation In decimal notation we can get around this problem using scientific notation or floating point notation. Number Scientific notation Floating-point notation 1, 245, 000, 000 1. 245 1012 0. 1245 1013 0. 0000001245 10 -7 0. 1245 10 -6 -0. 0000001245 -1. 245 10 -7 -0. 1245 10 -6 40

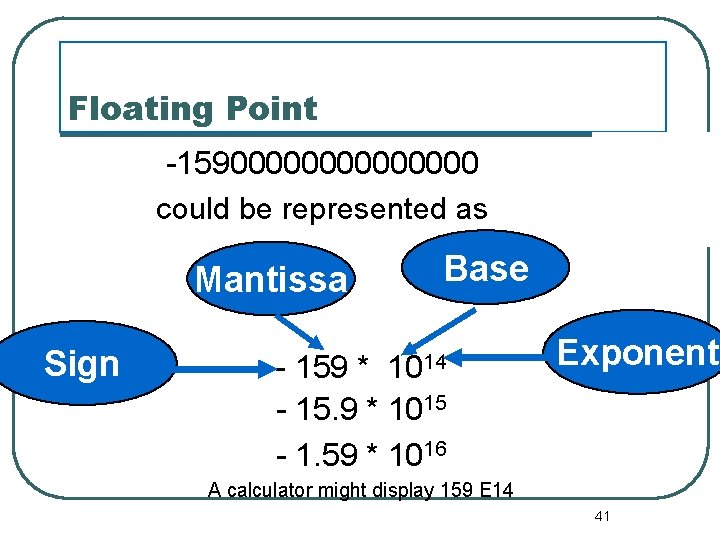
Floating Point -1590000000 could be represented as Mantissa Sign Base - 159 * 1014 - 15. 9 * 1015 - 1. 59 * 1016 Exponent A calculator might display 159 E 14 41

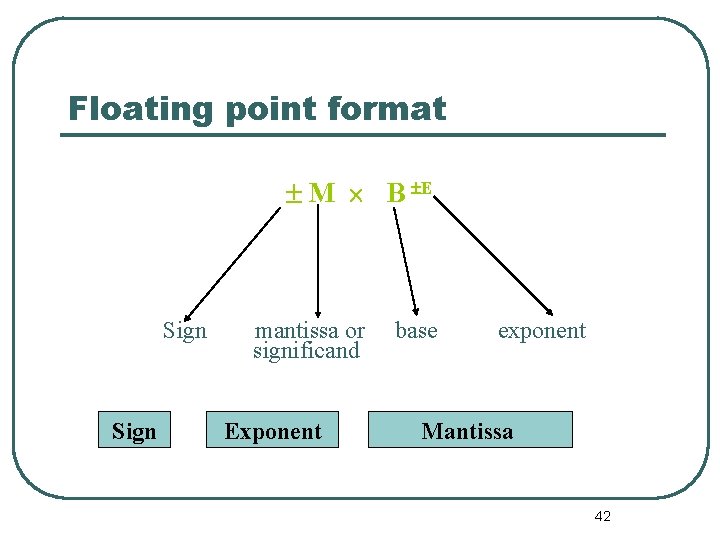
Floating point format M B E Sign mantissa or significand Exponent base exponent Mantissa 42

Floating Point Representation format Sign Exponent Mantissa The exponent is biased by a fixed value b, called the bias. The mantissa should be normalised, e. g. if the real mantissa if of the form 1. f then the normalised mantissa should be f, where f is a binary sequence. 43

IEEE 745 Single Precision The number will occupy 32 bits The first bit represents the sign of the number; 1= negative 0= positive. The next 8 bits will specify the exponent stored in biased 127 form. The remaining 23 bits will carry the mantissa normalised to be between 1 and 2. i. e. 1<= mantissa < 2 44

Representation in IEEE 754 single precision sign bit: • 0 for positive and, • 1 for negative numbers 8 biased exponent by 127 23 bit normalised mantissa Sign Exponent Mantissa 45

Basic Conversion Converting a decimal number to a floating point number. • 1. Take the integer part of the number and generate • • the binary equivalent. 2. Take the fractional part and generate a binary fraction 3. Then place the two parts together and normalise. 46

IEEE – Example 1 Convert 6. 75 to 32 bit IEEE format. 1. The Mantissa. The Integer first. 6/2 =3 r 0 3/2 =1 r 1 = 1102 1/2 =0 r 1 2. Fraction next. = 0. 112. 75 * 2 = 1. 5. 5 * 2 = 1. 0 3. put the two parts together… 110. 11 Now normalise 1. 1011 * 22 47

IEEE – Example 1 Convert 6. 75 to 32 bit IEEE format. 1. The Mantissa. The Integer first. 6/2 =3 r 0 3 / 2 = 1 r 1 = 1102 1/2 =0 r 1 2. Fraction next. . 75 * 2 = 1. 5. 5 * 2 = 1. 0 = 0. 112 3. put the two parts together… Now normalise 110. 11 1. 1011 * 22 48

IEEE – Example 1 Convert 6. 75 to 32 bit IEEE format. 1. The Mantissa. The Integer first. 6/2 =3 r 0 3/2 =1 r 1 = 1102 1/2 =0 r 1 2. Fraction next. . 75 * 2 = 1. 5. 5 * 2 = 1. 0 = 0. 112 3. put the two parts together… Now normalise 110. 11 1. 1011 * 22 49

IEEE Biased 127 Exponent To generate a biased 127 exponent Take the value of the signed exponent and add 127. Example. 216 then 2127+16 = 2143 and my value for the exponent would be 143 = 100011112 So it is simply now an unsigned value. . 50

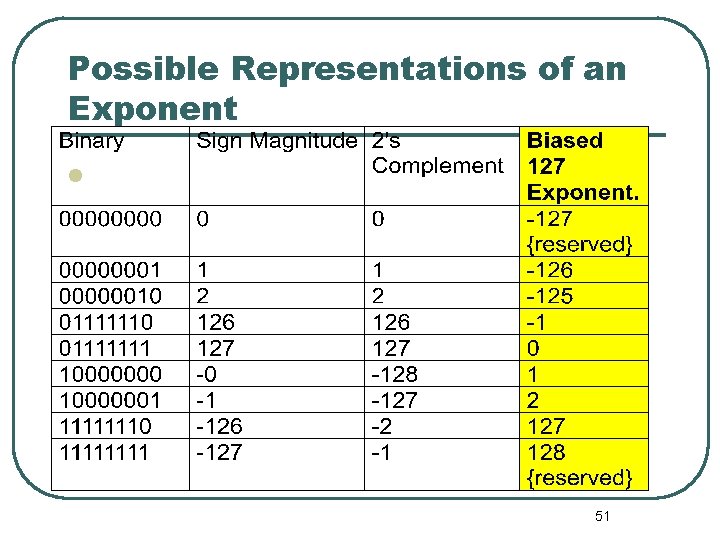
Possible Representations of an Exponent 51

Why Biased ? The smallest exponent 0000 Only one exponent zero 01111111 The highest exponent is 1111 To increase the exponent by one simply add 1 to the present pattern. 52

Back to the example Our original example revisited…. 1. 1011 * 22 Exponent is 2+127 =129 or 10000001 in binary. NOTE: Mantissa always ends up with a value of ‘ 1’ before the Dot. This is a waste of storage therefore it is implied but not actually stored. 1. 1000 is stored. 1000 6. 75 in 32 bit floating point IEEE representation: 0 10000001 10110000000000 sign(1) exponent(8) mantissa(23) 53

Representation in IEEE 754 single precision sign bit: • 0 for positive and, • 1 for negative numbers 8 biased exponent by 127 23 bit normalised mantissa Sign Exponent Mantissa 54

Example (2) which number does the following IEEE single precision notation represent? 1 1000 0100 0000 000 The sign bit is 1, hence it is a negative number. The exponent is 1000 0000 = 12810 It is biased by 127, hence the real exponent is 128 – 127 = 1. The mantissa: 0100 0000 000. It is normalised, hence the true mantissa is 1. 01 = 1. 2510 Finally, the number represented is: -1. 25 x 21 = -2. 50 55

Single Precision Format The exponent is formatted using excess-127 notation, with an implied base of 2 • Example: • • Exponent: 10000111 Representation: 135 – 127 = 8 The stored values 0 and 255 of the exponent are used to indicate special values, the exponential range is restricted to 2 -126 to 2127 The number 0. 0 is defined by a mantissa of 0 together with the special exponential value 0 The standard allows also values +/-∞ (represented as mantissa +/-0 and exponent 255 Allows various other special conditions 56

In comparison The smallest and largest possible 32 -bit integers in two’s complement are only -232 and 231 - 1 2021/12/18 PITT CS 1621 57 57

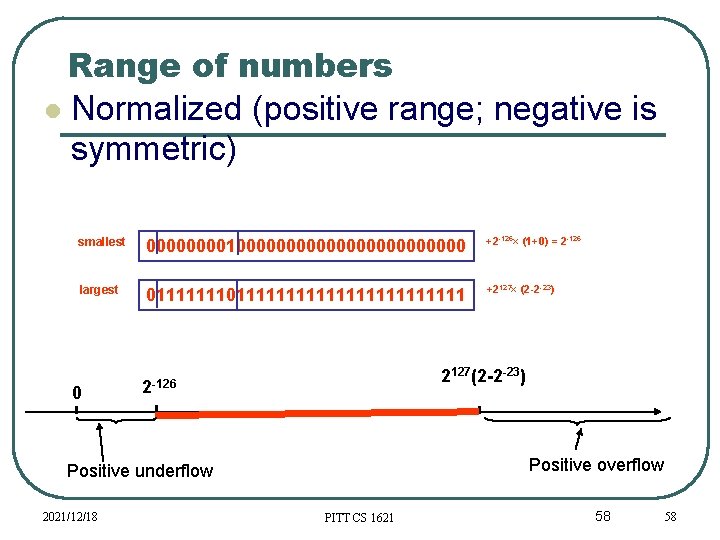
Range of numbers Normalized (positive range; negative is symmetric) smallest 00001000000000000 +2 -126× (1+0) = 2 -126 largest 0111111111111111 +2127× (2 -2 -23) 0 2127(2 -2 -23) 2 -126 Positive overflow Positive underflow 2021/12/18 PITT CS 1621 58 58

Representation in IEEE 754 double precision format It uses 64 bits • 1 bit sign • 11 bit biased exponent • 52 bit mantissa Sign Exponent Mantissa 59

IEEE 754 double precision Biased = 1023 11 -bit exponent with an excess of 1023. For example: • If the exponent is -1 • we then add 1023 to it. -1+1023 = 1022 • We then find the binary representation of 1022 • • Which is 0111 110 • The exponent field will now hold 0111 110 This means that we just represent -1 with an excess of 1023. 60

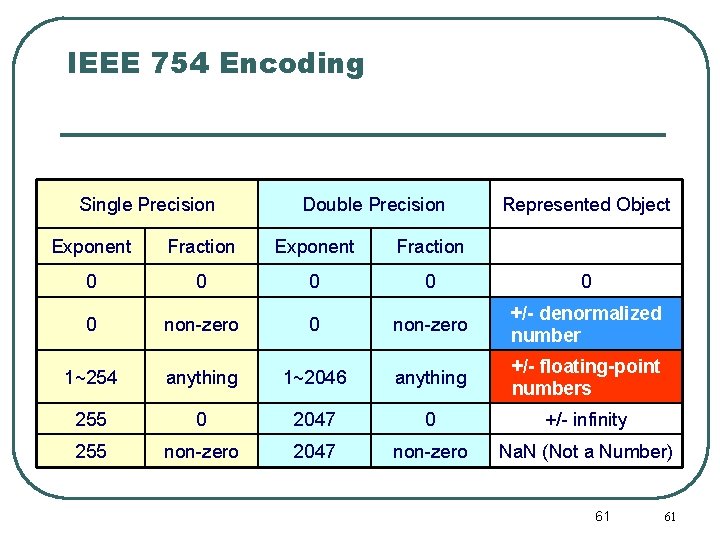
IEEE 754 Encoding Single Precision Double Precision Represented Object Exponent Fraction 0 0 0 non-zero +/- denormalized number 1~254 anything 1~2046 anything +/- floating-point numbers 255 0 2047 0 +/- infinity 255 non-zero 2047 non-zero Na. N (Not a Number) 61 61

Floating Point Representation format (summary) Sign Exponent Mantissa the sign bit represents the sign 0 for positive numbers 1 for negative numbers The exponent is biased by a fixed value b, called the bias. The mantissa should be normalised, e. g. if the real mantissa if of the form 1. f then the normalised mantissa should be f, where f is a binary sequence. • • 62

Character representation- ASCII (American Standard Code for Information Interchange) It is the scheme used to represent characters. Each character is represented using 7 -bit binary code. If 8 -bits are used, the first bit is always set to 0 See (table 5. 1 p 56, study guide) for character representation in ASCII. 63

ASCII – example Symbol decimal Binary 7 8 9 : ; < = > ? @ A B C 55 56 57 58 59 60 61 62 63 64 65 66 67 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111 01000000 01000001 01000010 01000011 64

Character strings How to represent character strings? A collection of adjacent “words” (bit-string units) can store a sequence of letters 'H' 'e' 'l' o' ' ' 'W' 'o' 'r' 'l' 'd' '' Notation: enclose strings in double quotes Representation convention: null character defines end of string • "Hello world" • Null is sometimes written as '' • Its binary representation is the number 0 65

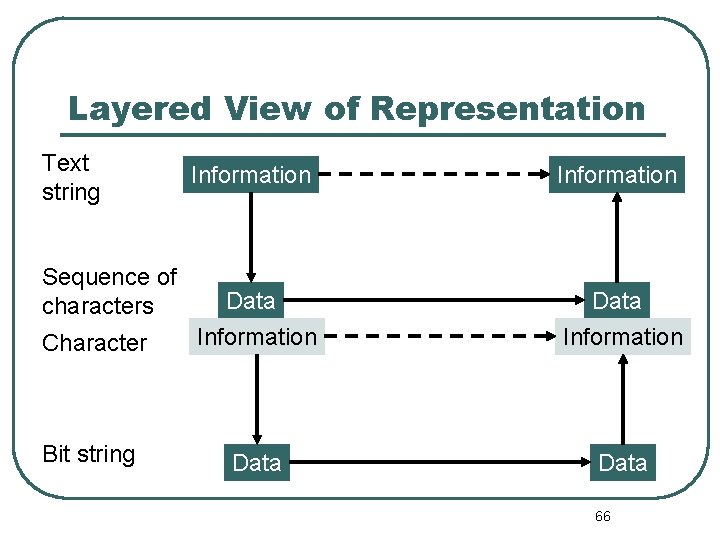
Layered View of Representation Text string Information Character Data Information Bit string Data Sequence of characters 66

Working With A Layered View of Representation Represent “SI” at the two layers shown on the previous slide. Representation schemes: • • Top layer - Character string to character sequence: Write each letter separately, enclosed in quotes. End string with ‘’. Bottom layer - Character to bit-string: Represent a character using the binary equivalent according to the ASCII table provided. 67

Solution SI ‘S’ ‘I’ ‘’ 0101001000000 • The colors are intended to help you read it; computers don’t care that all the bits run together. 68

exercise Use the ASCII table to write the ASCII code for the following: • CIS 110 • 6=2*3 69

Unicode - representation ASCII code can represent only 128 = 27 characters. It only represents the English Alphabet plus some control characters. Unicode is designed to represent the worldwide interchange. It uses 16 bits and can represents 32, 768 characters. For compatibility, the first 128 Unicode are the same as the one of the ASCII. 70

Colour representation Colours can represented using a sequence of bits. 256 colours – how many bits? • Hint for calculating • • To figure out how many bits are needed to represent a range of values, figure out the smallest power of 2 that is equal to or bigger than the size of the range. That is, find x for 2 x => 256 24 -bit colour – how many possible colors can be represented? • Hints • 16 million possible colours (why 16 millions? ) 71

24 -bits -- the True colour • 24 -bit color is often referred to as the true • colour. Any real-life shade, detected by the naked eye, will be among the 16 million possible colours. 72

Example: 2 -bit per pixel 4=22 choices • 00 (off, off)=white • 01 (off, on)=light • • grey 10 (on, off)=dark grey 11 (on, on)=black 0 0 = (white) = (light grey) 0 1 = 1 0 = 1 (dark grey) (black) 1 73

Image representation An image can be divided into many tiny squares, called pixels. Each pixel has a particular colour. The quality of the picture depends on two factors: • the density of pixels. • The length of the word representing colours. The resolution of an image is the density of pixels. The higher the resolution the more information the image contains. 74

Bitmap Images Each individual pixel (pi(x)cture element) in a graphic stored as a binary number • • Pixel: A small area with associated coordinate location Example: each point below is represented by a 4 -bit code corresponding to 1 of 16 shades of gray 75

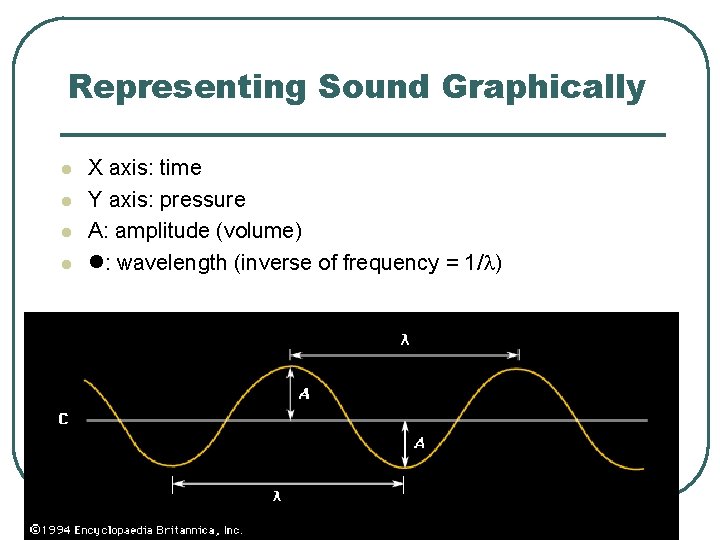
Representing Sound Graphically X axis: time Y axis: pressure A: amplitude (volume) : wavelength (inverse of frequency = 1/ ) 76

Sampling is a method used to digitise sound waves. A sample is the measurement of the amplitude at a point in time. The quality of the sound depends on: • The sampling rate, the faster the better • The size of the word used to represent a sample. 77

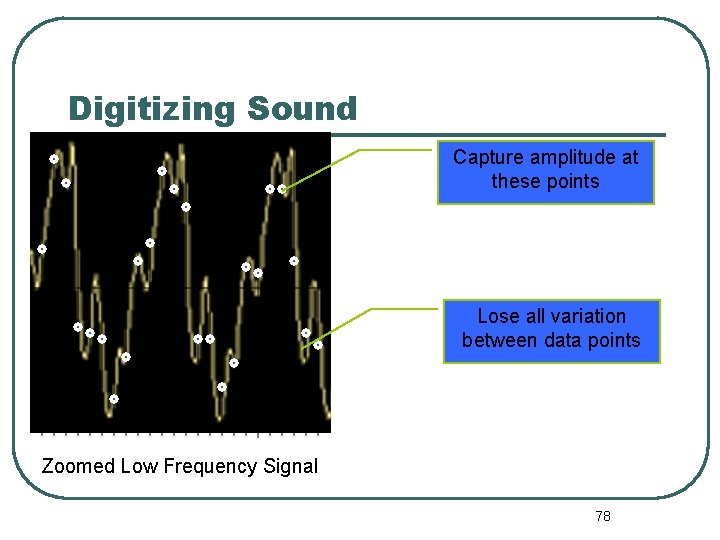
Digitizing Sound Capture amplitude at these points Lose all variation between data points Zoomed Low Frequency Signal 78

Summary Integer representation • • Unsigned, Signed, Excess notation, and Two’s complement. Fraction representation • Floating point (IEEE 754 format ) • Single and double precision Character representation Colour representation Sound representation 79

Exercise 1. Represent +0. 8 in the following floatingpoint representation: • • • 2. 3. 1 -bit sign 4 -bit exponent 6 -bit normalised mantissa (significand). Convert the value represented back to decimal. Calculate the relative error of the representation. 80