Chapter 5 Boolean Algebra and Reduction Techniques William

Chapter 5 Boolean Algebra and Reduction Techniques William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Combinational Logic • Using two or more logic gates to form a more useful, complex function • A combination of logic functions B = KD + HD • Boolean Reduction B = D(K+H) William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Boolean Laws and Rules • Commutative law of addition A+B=B+A • Associative law of addition A + (B + C) = (A + B) + C • Distributive law A(B + C) = AB + AC • Equivalent circuits – See Figures 5 -9 to 5 -14 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

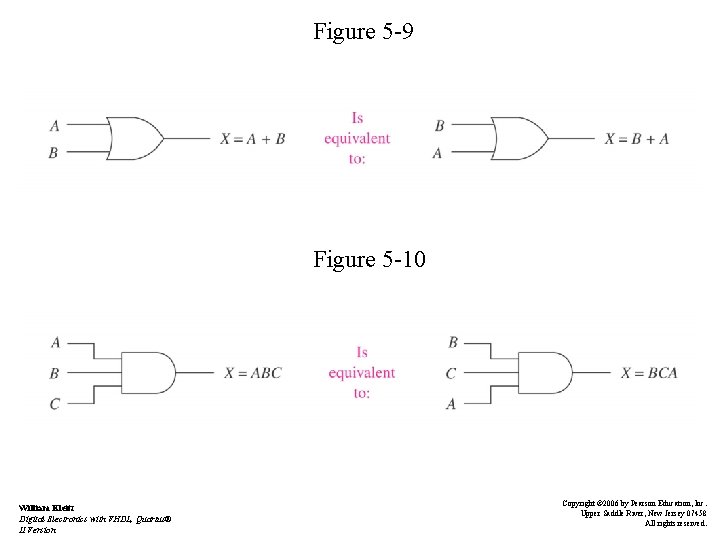
Figure 5 -9 Figure 5 -10 William Kleitz Digital Electronics with VHDL, Quartus® II

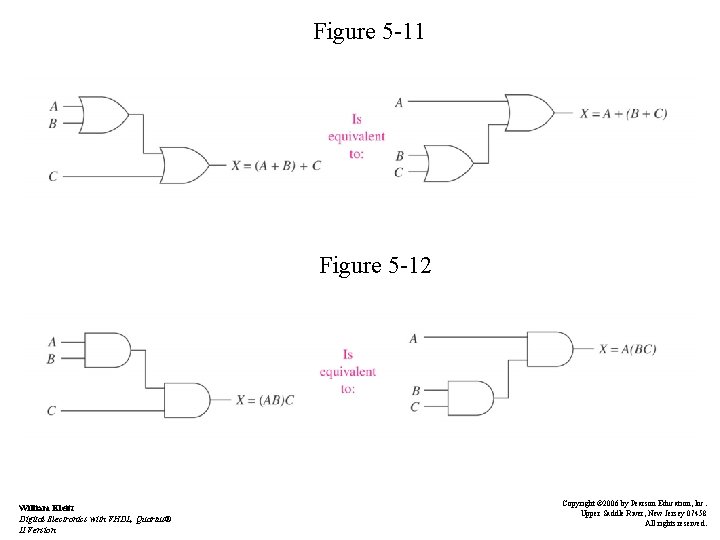
Figure 5 -11 Figure 5 -12 William Kleitz Digital Electronics with VHDL, Quartus® II

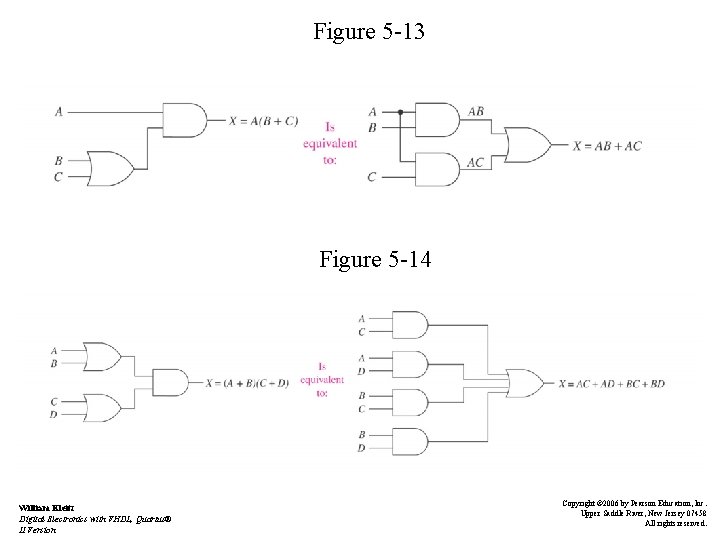
Figure 5 -13 Figure 5 -14 William Kleitz Digital Electronics with VHDL, Quartus® II

Boolean Laws and Rules • Rule 1: Anything ANDed with a 0 is equal to 0 • Rule 2: Anything ANDed with a 1 is equal to itself - Figure 5 -16 • Rule 3: Anything ORed with a 0 is equal to itself - Figure 5 -17 • Rule 4: Anything ORed with a 1 is equal to 1 - Figure 5 -18 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

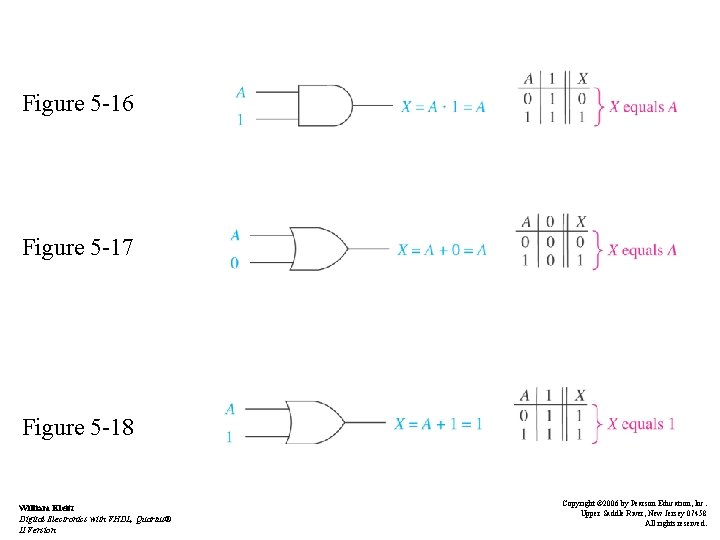
Figure 5 -16 Figure 5 -17 Figure 5 -18 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Boolean Laws and Rules • Rule 5: Anything ANDed with itself is equal to itself - Figure 5 -19 • Rule 6: Anything ORed with itself is equal to itself - Figure 5 -20 • Rule 7: Anything ANDed with its own complement equals 0 - Figure 5 -21 • Rule 8: Anything ORed with its own complement equals 1 - Figure 5 -22 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

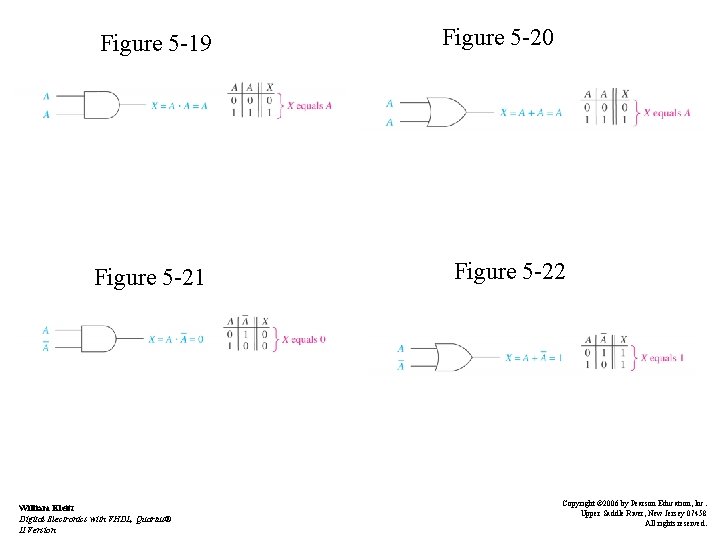
Figure 5 -19 Figure 5 -21 William Kleitz Digital Electronics with VHDL, Quartus® II Version Figure 5 -20 Figure 5 -22 Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

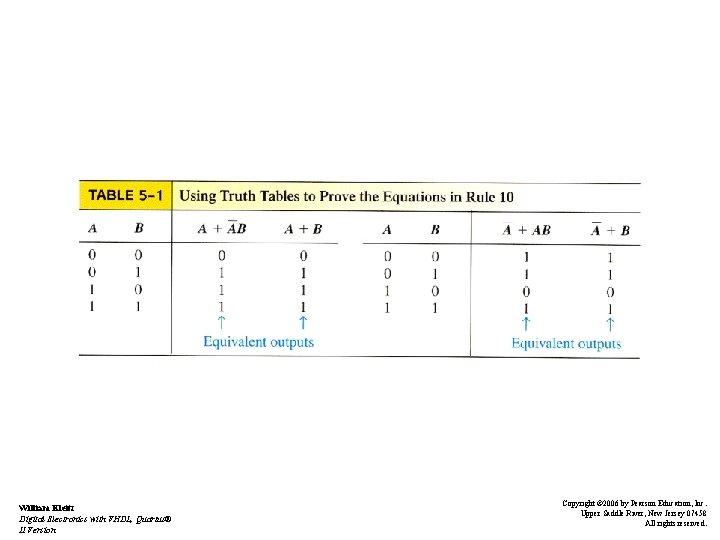
Boolean Laws and Rules • Rule 9: Anything complemented twice will return to its original logic level - Figure 523 • Rule 10: – A + AB = A + B – See Table 5 -1 • Law and Rule Summary - See Table 5 -2 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

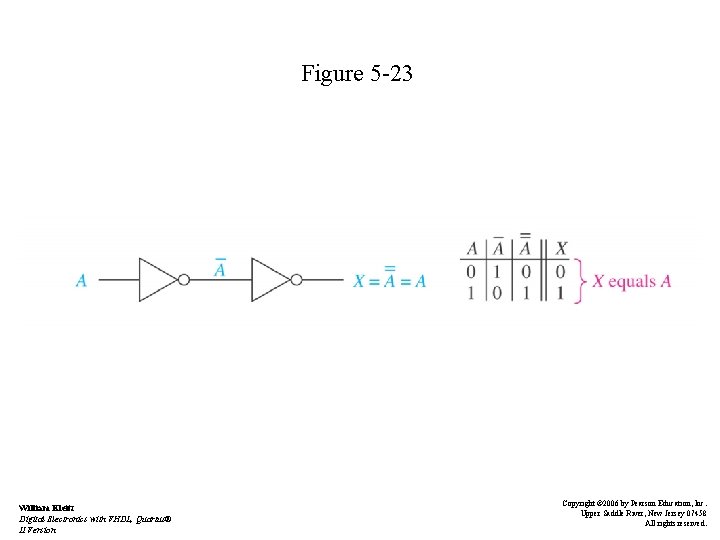
Figure 5 -23 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright ©

William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson

Simplification of Combinational Logic Circuits Using Boolean Algebra • Equivalent circuits can be formed with fewer gates • Cost is reduced • Reliability is improved • Use laws and rules of Boolean Algebra William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Using Quartus II To Determine Simplified Equations • The software will determine the simplest form before synthesizing – eliminates unnecessary inputs – minimizes gates used in CPLD • Quartus II solution to example 5 -9 – see figures 5 -32 (a) and (b) William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Figures 5 -32 (a) and (b) William Kleitz Digital Electronics with VHDL, Quartus® II

Using Quartus II To Determine Simplified Equations • If the program determines an input is not necessary, a warning message will be displayed when the program is compiled – See figure 5 -33 • The floor plan view provides implementation details – The Equations Section, see figure 5 -35 – Arithmetic operators: • • & AND ! NOT # OR $ Exclusive OR William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Using Quartus II To Determine Simplified Equations • Floorplan Editor Display – alternate way to view reduced logic equation – useful for viewing and modifying pin and macrocell assignments • Logic Array Block (LAB) view shows interconnections and equations • See figure 5 -36(b) William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

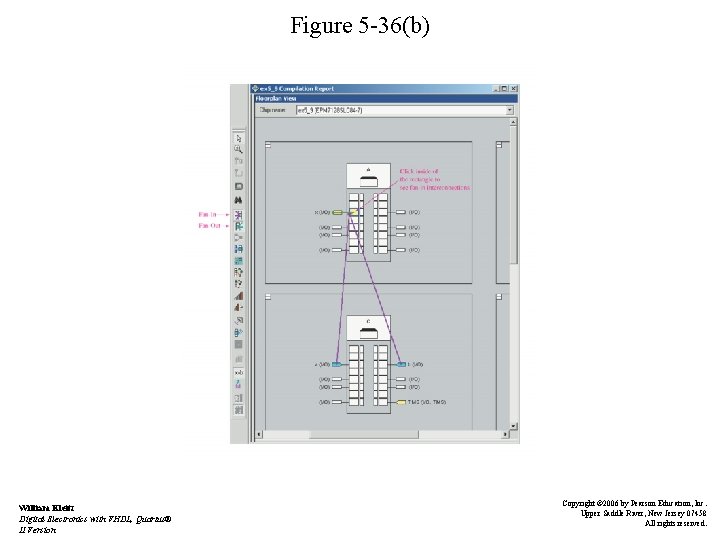
Figure 5 -36(b) William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright ©

De. Morgan’s Theorem • To simplify circuits containing NAND and NOR gates • AB=A+B • A+B=AB William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

De. Morgan’s Theorem • Break the bar over the variables and change the sign between them • Inversion bubbles - used to show inversion rather than inverters • Use parentheses to maintain proper groupings • End up with Sum-of-Products (SOP) form William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

De. Morgan’s Theorem • Bubble Pushing – See Figure 5 -60 – shortcut method of forming equivalent gates – change the logic gate • (AND to OR or OR to AND) – Add bubbles to the inputs and outputs where there were none and remove original bubbles William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

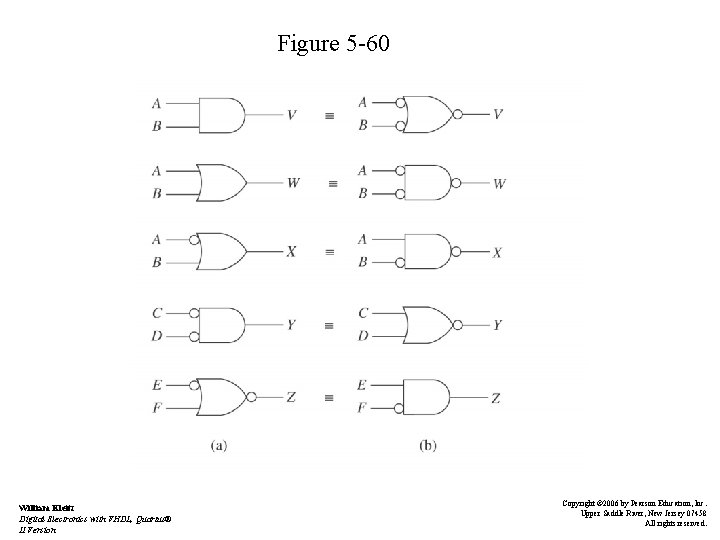
Figure 5 -60 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright ©

Entering a Truth Table in VHDL Using a Vector Signal • Truth table to be entered, table 5 -5 – define internal signal to represent the three inputs – the three inputs will be grouped as a 3 bit vector – the use of comments to document a program – use selected signal assignments, built to look like truth table entries • see figure 5 -62 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Figure 5 -62 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright ©

The Universal Capability of NAND and NOR Gates • NANDs can be combined to form all other gates – See Figures 5 -68, -69, -71, -73, and -74 • NORs can be combined to form all other gates – See Figure 5 -75 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

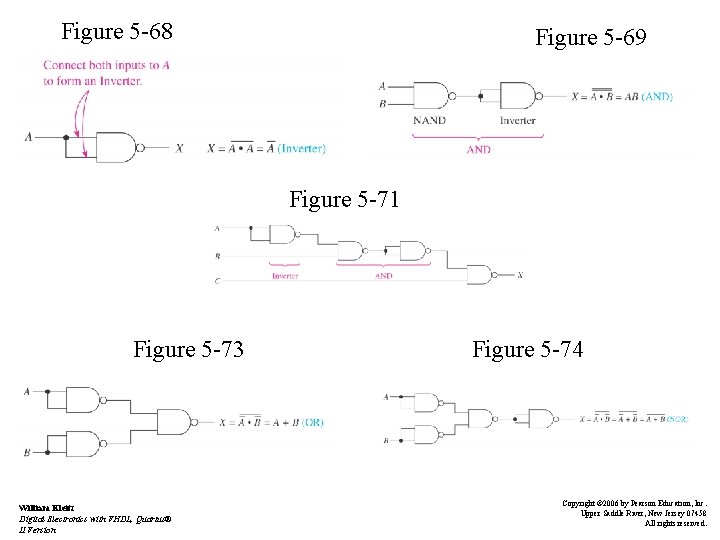
Figure 5 -68 Figure 5 -69 Figure 5 -71 Figure 5 -73 William Kleitz Digital Electronics with VHDL, Quartus® II Version Figure 5 -74 Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

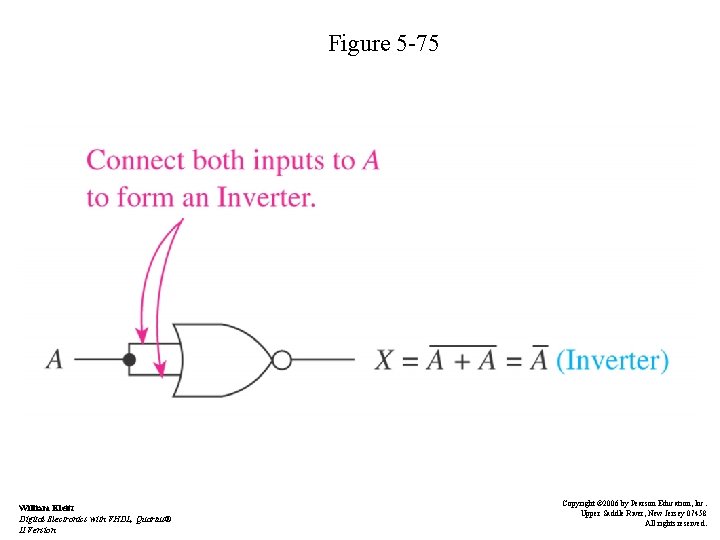
Figure 5 -75 William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright ©

AND-OR-INVERT Gates for Implementing Sum-of-Products Expressions • Product-of-sums (POS) form • Sum-of-products (SOP) form – can easily be implemented using an AOI gate • TTL and CMOS AOI devices are available William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Karnaugh Mapping • • • To minimize the number of gates Reduce circuit cost Reduce physical size Reduce gate failures Requires SOP form William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Karnaugh Mapping • Graphically shows output level for all possible input combinations • Moving from one cell to an adjacent cell, only one variable changes William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Karnaugh Mapping • Transform the Boolean equation into SOP form • Fill in the appropriate cells of the K-map • Encircle adjacent cells in groups of 2, 4 or 8 – watch for wraparound • Find terms by which variables remain constant within circles William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

System Design Applications • Use Karnaugh Mapping to reduce equations • Use AND-OR-INVERT gates to implement logic William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Summary • Several logic gates can be connected together to form combinational logic. • There are several Boolean laws and rules that provide the means to form equivalent circuits. • Boolean algebra is used to reduce logic circuits to simpler equivalent circuits that function identically to the original circuit. William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Summary • De. Morgan’s theorem is required in the reduction process whenever inversion bars cover more than one variable in the original Boolean equation. • NAND and NOR gates are sometimes referred to as universal gates, because they can be used to form any of the other gates. William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Summary • AND-OR-INVERT (AOI) gates are often used to implement sum-of-products (SOP) equations • Karnaugh mapping provides a systematic method of reducing logic circuits. William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Summary • Combinational logic designs can be entered into a computer using graphic design software or VHDL. • Using vectors in VHDL is a convenient way to group like signals together similar to an array. William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.

Summary • Truth tables can be implemented in VHDL using vector signals with the selected signal assignment statement. • Quartus II can be used to determine the simplified equation of combinational circuits. William Kleitz Digital Electronics with VHDL, Quartus® II Version Copyright © 2006 by Pearson Education, Inc. Upper Saddle River, New Jersey 07458 All rights reserved.