Chapter 5 Basic Data Representation https vtk orgdocumentation

Chapter 5 Basic Data Representation https: //vtk. org/documentation/

Characteristics of Data • Discrete Interpolation P 1, P 2 • Regular/Irregular • Data Dimensions

Data Structure Design Criterion Data Structure • Compact (save space) • Efficient (fast retrieval) • Map-able (easy to convert) • Minimal Coverage (small foot prints) • Simple (easy to use)

Dataset • Data objects in the visualization pipeline are called datasets • consisting of two pieces: an organizing structure and supplemental data attributes.

Dataset Structure: topology and geometry • Topology: is the set of properties invariant under certain geometric transformations. • Geometry: is the instantiation of the topology; the specification of positions in a 3 D space. • VTK Model: the structure consists of cells and points. The cells specify the topology; while the points specify the geometry

Dataset Attribute: • Data to be visualized. • Associated with each point. • Typical attributes: scalars, vectors, normals, texture coordinates, tensors, and user-defined data.

Cell Types • A data set consists of one or more cells • A cell is defined by a “type” and an ordered list of point • Type: topology, cell type • Ordered list: geometry, points • Together: organizational structure • Use Set: all the cells using a point: U(pi) = {Ci: pi Ci}

Cell Types Vertex: zero-dimensional cell, It is defined by a single point. vtk. Vertex Line: one dimensional cell. It is defined by two points. vtk. Line Polyline: is a composite one-dimensional cell consisting of n connected lines. It is defined by an ordered list of n+1 points. vtk. Poly. Line Triangle: is a primary two-dimensional cell. The triangle is defined by a counter-clockwise ordered list of three points. vtk. Triangle Polygon: is a primary two-dimensional cell. The polygon is defined by an ordered list of three or more points lying in a plane Tetrahedron: is a primary three-dimensional cell. It is defined by a list of four nonplanar point. Vtk. Tetrahedron

Attribute Data q Attribute data is information associated with the structure of the dataset. It is what to be visualized. q Dataset Attribute Model § § § Scalars Vectors Normals Texture Coordinates Tensors (The rank of a tensor is the dimension of the matrix containing its values. ) User-defined

Type of Datasets Dependent on topology of the dataset. Uniform Grid (uniform in each direction, vtk. Image. Data) q Parameters: § Dimension: nx, ny, nz § Origin: x 0, y 0, z 0 § Spacing: dx, dy, dz

Type of Datasets: Uniform Grid q IJK space § x = i*dx + x 0 § y = j*dy + y 0 § z = k*dz + z 0 q Data array (i, j, k), loop i first, then j, k last. q Simple, compact and speedy retrieval. q Not flexible q Represented by vtk. Image. Data in VTK. Example: Fig. 5 -18.

Rectlinear Grid q Dimension: nx, ny, nz q Nonuniform spacing, but straight grid lines. float x[44]={0. 0, 1. 2, 2. 8, 3. 9……. } float y[33]={1. 0, ……………} float z[22]={0. 8, ……………}

Rectlinear Grid q IJK space. x = x[I]; y = y[J]; z = z[K]; q Data array (i, j, k), i changes first, then j, k last. q Simple q compact (takes O(nx + ny + nz) more space) q speedy retrieval q Little more flexible

Rectlinear Grid (Example Code) vtk. Float. Array * x. Coords=vtk. Float. Array: : New(); for(i=0; i<44; i++) x. Coords-> Insert. Next. Value(x[i]) vtk. Float. Array * y. Coords=vtk. Float. Array: : New(); for(i=0; i<33; i++) y. Coords-> Insert. Next. Value(y[i]) vtk. Float. Array * z. Coords=vtk. Float. Array: : New(); for(i=0; i<22; i++) z. Coords-> Insert. Next. Value(z[i]) vtk. Recti. Linear. Grid * rgrid=vtk. Recti. Linear. Grid: : New(); rgrid set. XCoordinates(x. Coords); rgrid set. YCoordinates(y. Coords); rgrid set. ZCoordinates(z. Coords); rgrid Set. Dimensions(44, 33, 22);

Structured Grid q Dimension: nx, ny, nz q Nonuniform spacing q IJK space (no formula) q Coordinates of each grid node need to be given. x(I, J, K), y(I, J, K), z(I, J, K)

Data Set: Internal Memory Structure in Generic Form

Unstructured Grid • No dimensions parameters: nx, ny, nz • No IJK space • Coordinates of each node need to be given • Most flexible, can represent any structures of data • Not compact (need space to save xyz values and cell information) • Slow retrieval

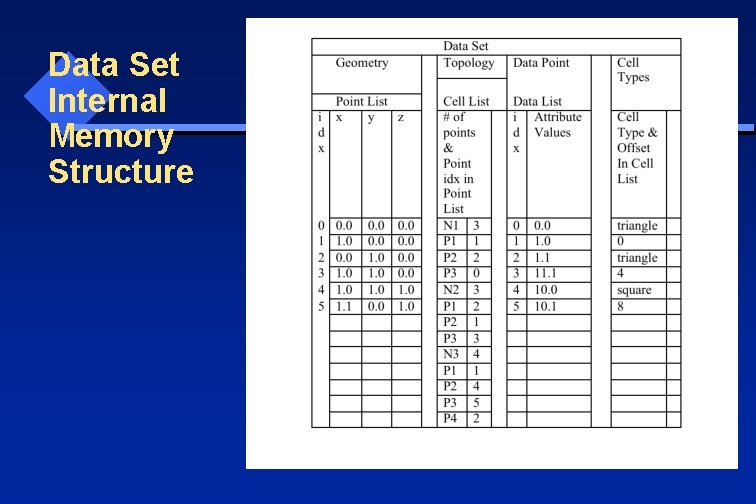
Data Set Internal Memory Structure

Unstructured Surface q Polygonal Surface (Poly. Data) q No dimensions parameters: nx, ny, nz q No IJK space q Coordinates of each node need to be given q Data value(s) on each node needs to be given

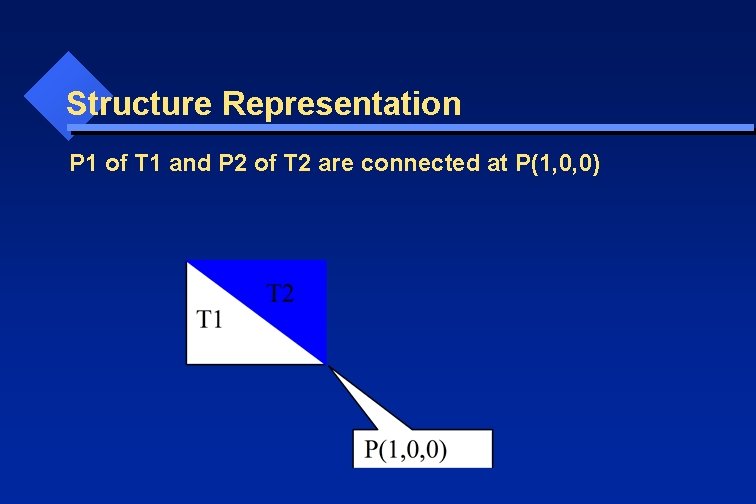
Structure Representation P 1 of T 1 and P 2 of T 2 are connected at P(1, 0, 0)

Structure Representation The Wrong Way: Making Copies class Tri { public: point P 1, P 2, P 3; }; Tri T 1, T 2; T 1. P 1. x=1. 0; T 1. P 1. y=0. 0; T 1. P 1. z=0. 0; ……. T 2. P 2. x=1. 0; T 2. P 2. y=0. 0; T 2. P 2. z=0. 0;

Structure Representation: Wrong Way Each triangle keeps a copy of the vertex values. Drawback: if the coordinate of P is changed, all cells having a copy of its value need to be updated.

Structure Representation: Correct Way Save the vertex values in an array (Point List). Store the indexes of the vertexes for each triangle in the triangle definition

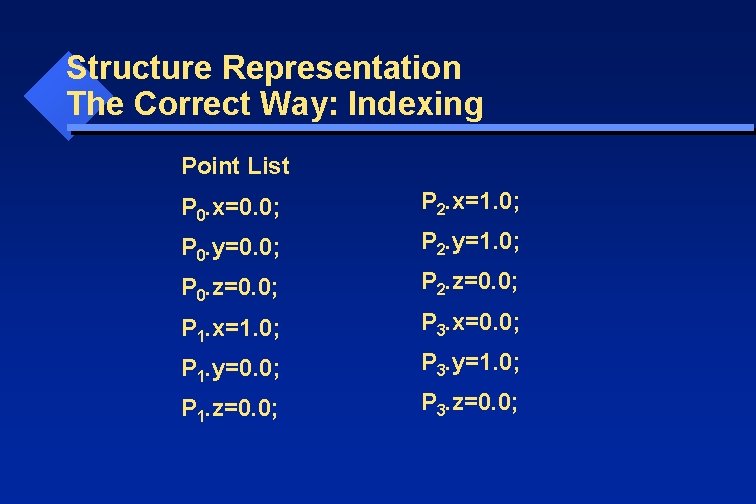
Structure Representation The Correct Way: Indexing Point List P 0. x=0. 0; P 2. x=1. 0; P 0. y=0. 0; P 2. y=1. 0; P 0. z=0. 0; P 2. z=0. 0; P 1. x=1. 0; P 3. x=0. 0; P 1. y=0. 0; P 3. y=1. 0; P 1. z=0. 0; P 3. z=0. 0;

Structure Representation The Correct Way: Indexing class Tri{ public: int ID 1, ID 2, ID 3; }; Tri T 1, T 2; T 1. ID 1=0; T 1. ID 2=1; T 1. ID 3=3; T 2. ID 1=1; T 2. ID 2=2; T 2. ID 3=3;

Structure Representation: The Correct Way: Indexing Each triangle keeps an index list (cell list) of its vertexes. If the coordinate of P is changed, none of the cells using it needs to be changed. Only the one copy of its value in the point list needs to be updated.

Dataset Structure: topology and geometry • Topology: is the set of properties invariant under certain geometric transformations. • Geometry: is the instantiation of the topology; the specification of positions in a 3 D space. • VTK Model: the structure consists of cells and points. The cells specify the topology; while the points specify the geometry

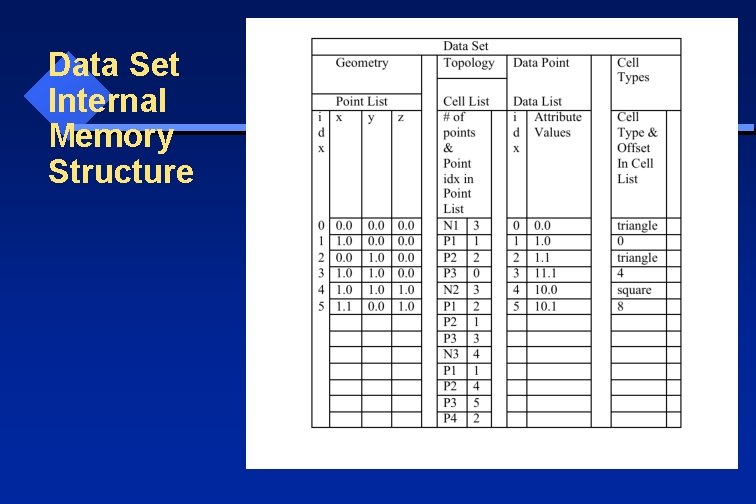
Data Set Internal Memory Structure

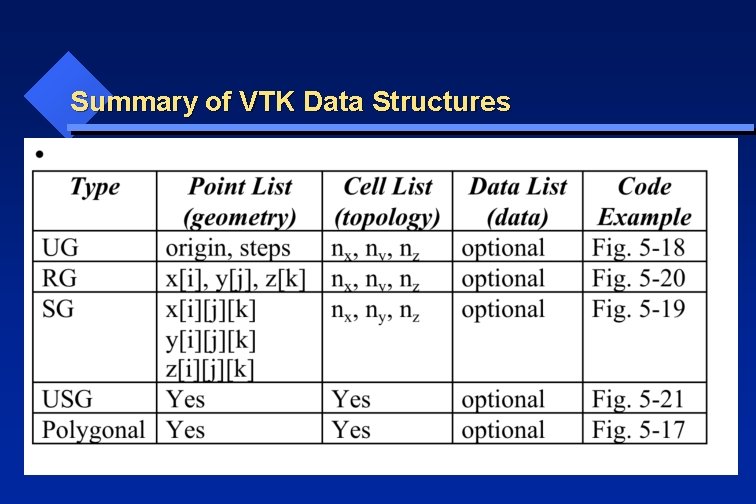
Summary of VTK Data Structures