Chapter 5 B Rotational Equilibrium A Power Point

The Golden Gate Bridge provides an excellent example of balanced forces and torques. Engineers must design such structures so that rotational and translational equilibrium is maintained. Photo © EP 101 Photodisk/Getty

Objectives: After completing this module, you should be able to: • State and describe with examples your understanding of the first and seconditions for equilibrium. • Write and apply the first and seconditions for equilibrium to the solution of physical problems similar to those in this module.

Translational Equilibrium Car at rest Constant speed The linear speed is not changing with time. There is no resultant force and therefore zero acceleration. Translational equilibrium exists.

Rotational Equilibrium Wheel at rest Constant rotation The angular speed is not changing with time. There is no resultant torque and, therefore, zero change in rotational velocity. Rotational equilibrium exists.

Equilibrium • An object is said to be in equilibrium if and only if there is no resultant force and no resultant torque. First Condition: Second Condition:

Does Equilibrium Exist? T 300 Is. YES! the system at left in Observation equilibrium bothof shows that no part and thetranslationally system is changing rotationally? its state of motion. A sky diver moments after the jump? Yes or No. No? A sky diver who reaches terminal speed? A fixed pulley rotating at constant speed? Yes

Statics or Total Equilibrium Statics is the physics that treats objects at rest or objects in constant motion. In this module, we will review the first condition for equilibrium (treated in Part 5 A of these modules); then we will extend our treatment by working with the secondition for equilibrium. Both conditions must be satisfied for true equilibrium.

Translational Equilibrium Only If all forces act at the same point, then there is no torque to consider and one need only apply the first condition for equilibrium: • Construct free-body diagram. • Sum forces and set to zero: SFx= 0; SFy= 0 • Solve for unknowns.

Review: Free-body Diagrams • Read problem; draw and label sketch. • Construct force diagram for each object, vectors at origin of x, y axes. • Dot in rectangles and label x and y components opposite and adjacent to angles. • Label all components; choose positive direction.

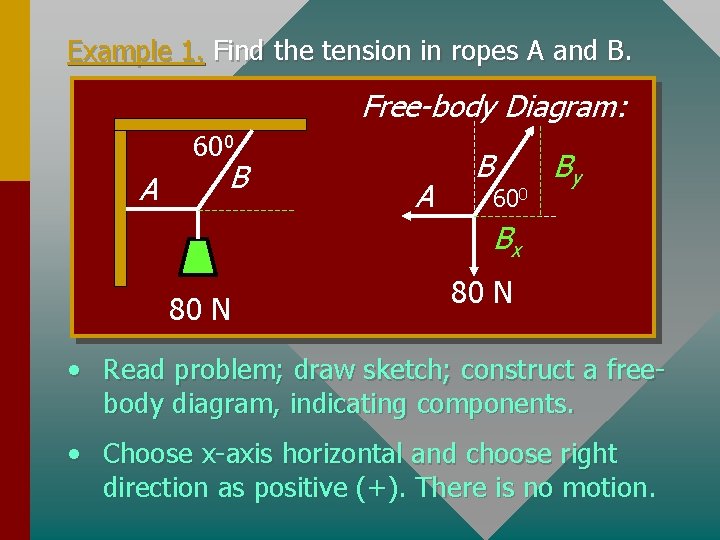
Example 1. Find the tension in ropes A and B. Free-body Diagram: 600 A B 600 By Bx 80 N • Read problem; draw sketch; construct a freebody diagram, indicating components. • Choose x-axis horizontal and choose right direction as positive (+). There is no motion.

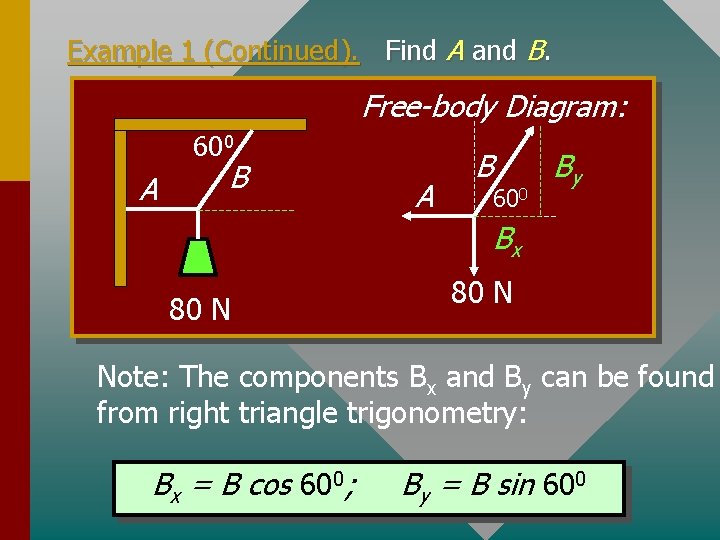
Example 1 (Continued). Find A and B. Free-body Diagram: 600 A B 600 By Bx 80 N Note: The components Bx and By can be found from right triangle trigonometry: Bx = B cos 600; By = B sin 600

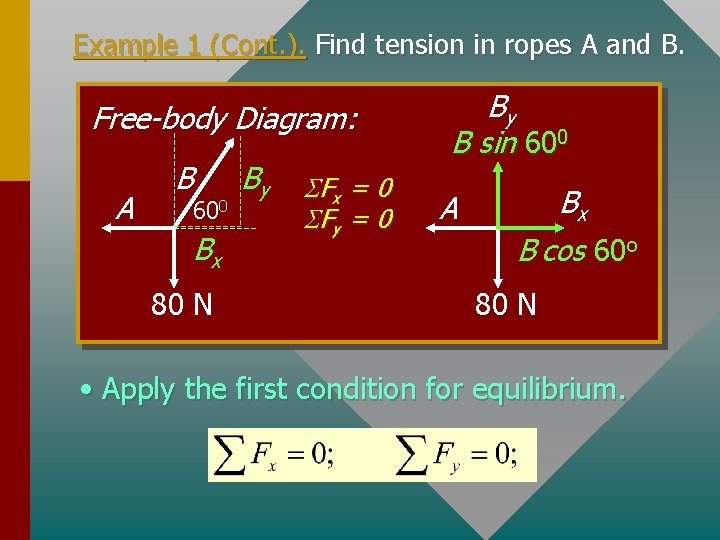
Example 1 (Cont. ). Find tension in ropes A and B. Free-body Diagram: A B 600 Bx 80 N By S Fx = 0 S Fy = 0 By B sin 600 Bx A B cos 60 o 80 N • Apply the first condition for equilibrium.

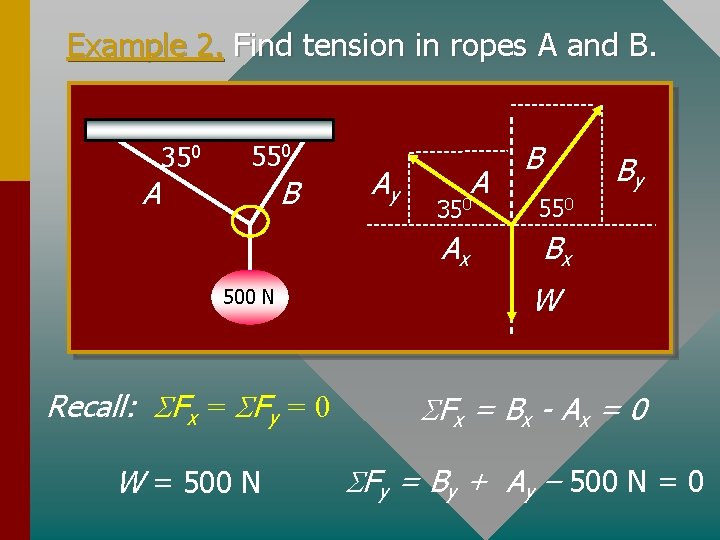
Example 2. Find tension in ropes A and B. A 350 550 B 500 N Ay A B By 350 550 Ax Bx W Recall: SFx = SFy = 0 SFx = Bx - Ax = 0 W = 500 N SFy = By + Ay – 500 N = 0

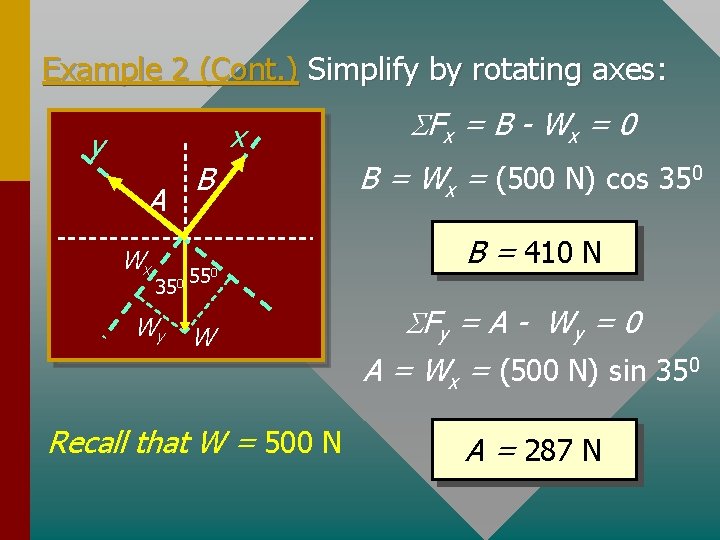
Example 2 (Cont. ) Simplify by rotating axes: x y A Wx 350 Wy B 550 W Recall that W = 500 N SFx = B - Wx = 0 B = Wx = (500 N) cos 350 B = 410 N SFy = A - Wy = 0 A = Wx = (500 N) sin 350 A = 287 N

Total Equilibrium In general, there are six degrees of freedom (right, left, up, down, ccw, and cw): ccw (+) cw (-) SFx= 0 Right = left SFx= 0 Up = down St=0 S t (ccw)= S t (ccw)

General Procedure: • Draw free-body diagram and label. • Choose axis of rotation at point where least information is given. • Extend line of action forces, find moment arms, and sum torques about chosen axis: St = t 1 + t 2 + t 3 +. . . = 0 • Sum forces and set to zero: SFx= 0; SFy= 0 • Solve for unknowns.

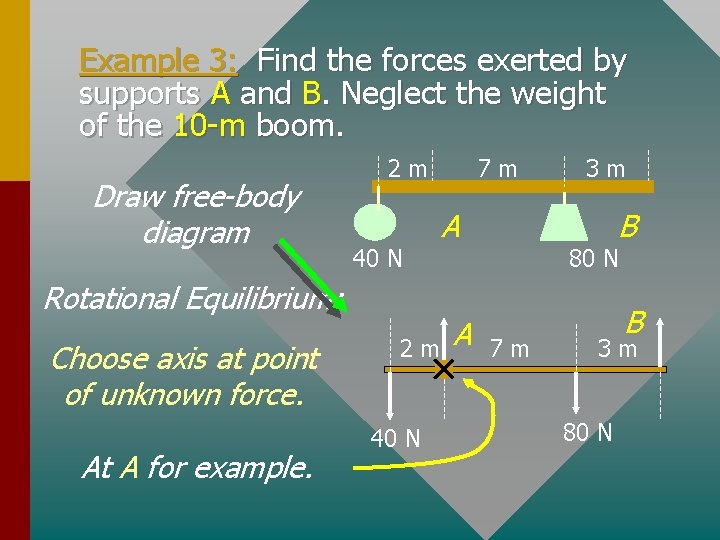
Example 3: Find the forces exerted by supports A and B. Neglect the weight of the 10 -m boom. Draw free-body diagram 2 m 40 N Rotational Equilibrium: Choose axis at point of unknown force. At A for example. 2 m 40 N 7 m A A 3 m B 80 N 7 m B 3 m 80 N

Example 3 (Cont. ) Note: When applying St(ccw) = St(cw) we need only the absolute (positive) magnitudes of each torque. (+) = (-) 2 m A 40 N 7 m B 3 m 80 N Torques about axis ccw are equal to those cw. ccw (+) cw (-) Essentially, we are saying that the torques are balanced about a chosen axis.

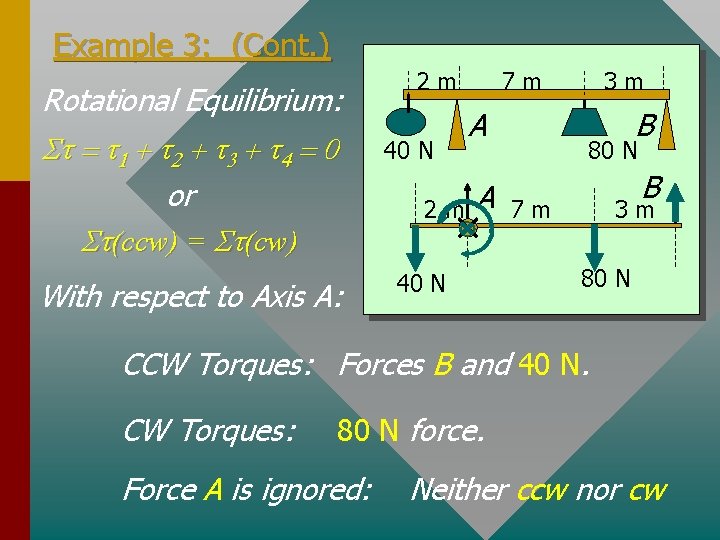
Example 3: (Cont. ) Rotational Equilibrium: St = t 1 + t 2 + t 3 + t 4 = 0 or St(ccw) = St(cw) With respect to Axis A: 7 m 2 m 40 N 2 m A A 40 N 3 m B 80 N B 7 m 3 m 80 N CCW Torques: Forces B and 40 N. CW Torques: 80 N force. Force A is ignored: Neither ccw nor cw

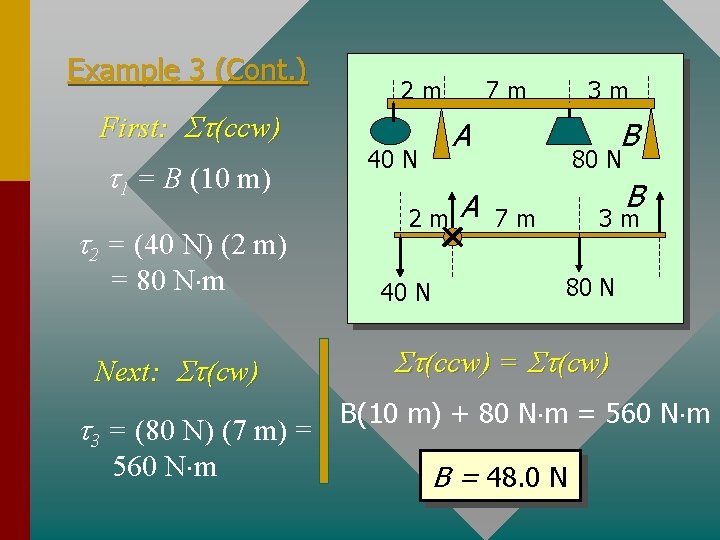
Example 3 (Cont. ) First: St(ccw) t 1 = B (10 m) t 2 = (40 N) (2 m) = 80 N m Next: St(cw) t 3 = (80 N) (7 m) = 560 N m 7 m 2 m A 40 N 2 m 40 N 3 m A B 80 N B 7 m 3 m 80 N St(ccw) = St(cw) B(10 m) + 80 N m = 560 N m B = 48. 0 N

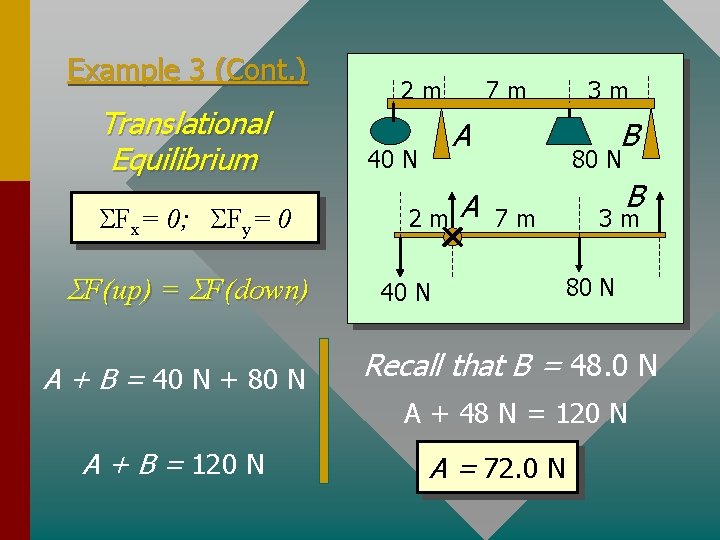
Example 3 (Cont. ) Translational Equilibrium SFx= 0; SFy= 0 SF(up) = SF(down) A + B = 40 N + 80 N A + B = 120 N 7 m 2 m A 40 N 2 m A 3 m B 80 N 7 m 40 N B 3 m 80 N Recall that B = 48. 0 N A + 48 N = 120 N A = 72. 0 N

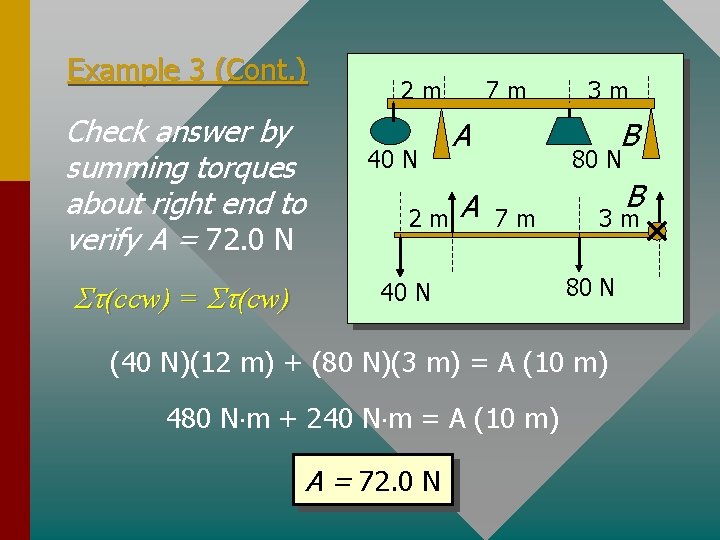
Example 3 (Cont. ) Check answer by summing torques about right end to verify A = 72. 0 N St(ccw) = St(cw) 7 m 2 m 40 N 2 m A A 3 m B 80 N 7 m 40 N B 3 m 80 N (40 N)(12 m) + (80 N)(3 m) = A (10 m) 480 N m + 240 N m = A (10 m) A = 72. 0 N

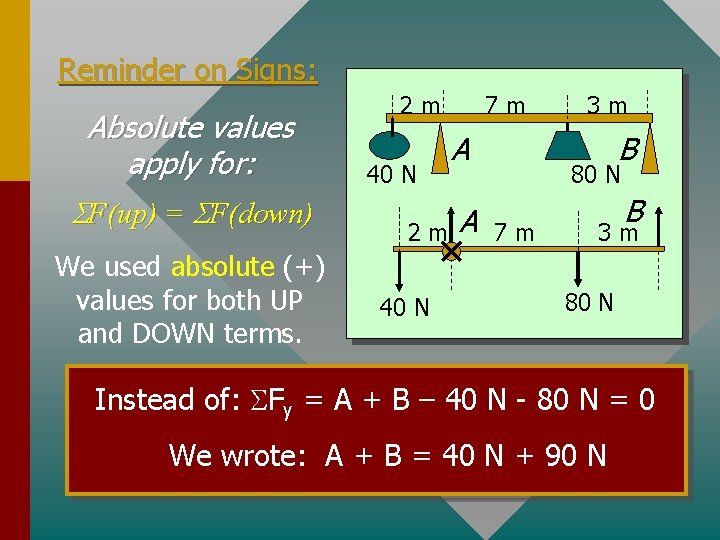
Reminder on Signs: Absolute values apply for: SF(up) = SF(down) We used absolute (+) values for both UP and DOWN terms. 7 m 2 m 40 N A A 3 m B 80 N 7 m B 3 m 80 N Instead of: SFy = A + B – 40 N - 80 N = 0 We wrote: A + B = 40 N + 90 N

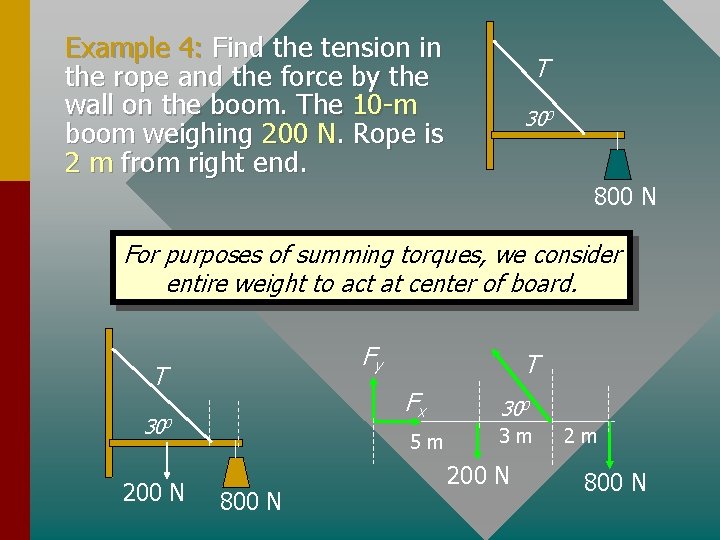
Example 4: Find the tension in the rope and the force by the wall on the boom. The 10 -m boom weighing 200 N. Rope is 2 m from right end. T 300 800 N For purposes of summing torques, we consider entire weight to act at center of board. Fy T 300 200 N 800 N T Fx 300 5 m 3 m 200 N 2 m 800 N

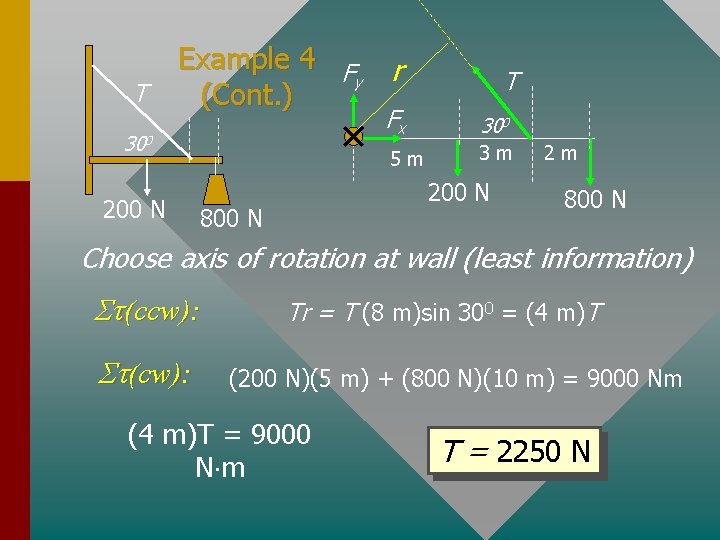
T Example 4 F r y (Cont. ) 300 200 N T Fx 300 5 m 3 m 200 N 800 N 2 m 800 N Choose axis of rotation at wall (least information) St(ccw): St(cw): Tr = T (8 m)sin 300 = (4 m)T (200 N)(5 m) + (800 N)(10 m) = 9000 Nm (4 m)T = 9000 N m T = 2250 N

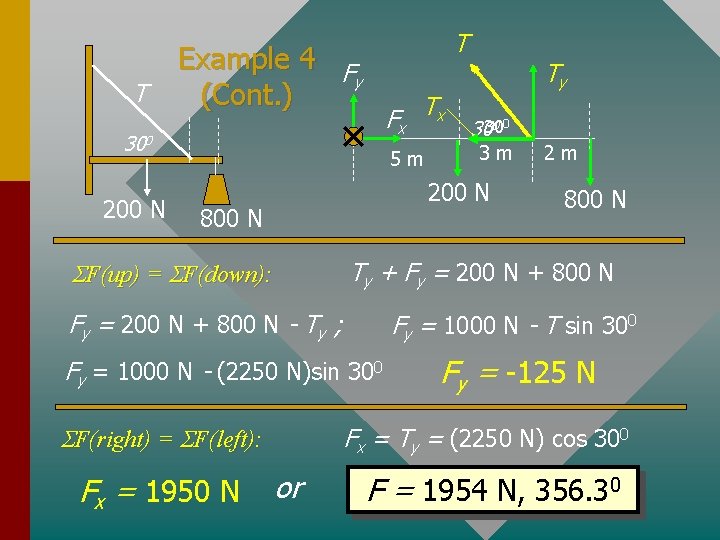
T T Example 4 F y (Cont. ) Fx T x 300 200 N 5 m 00 3030 3 m 200 N 800 N SF(up) = SF(down): 800 N Fy = 1000 N - T sin 300 Fy = 1000 N - (2250 N)sin 300 SF(right) = SF(left): 2 m Ty + Fy = 200 N + 800 N - Ty ; Fx = 1950 N Ty Fy = -125 N Fx = Ty = (2250 N) cos 300 or F = 1954 N, 356. 30

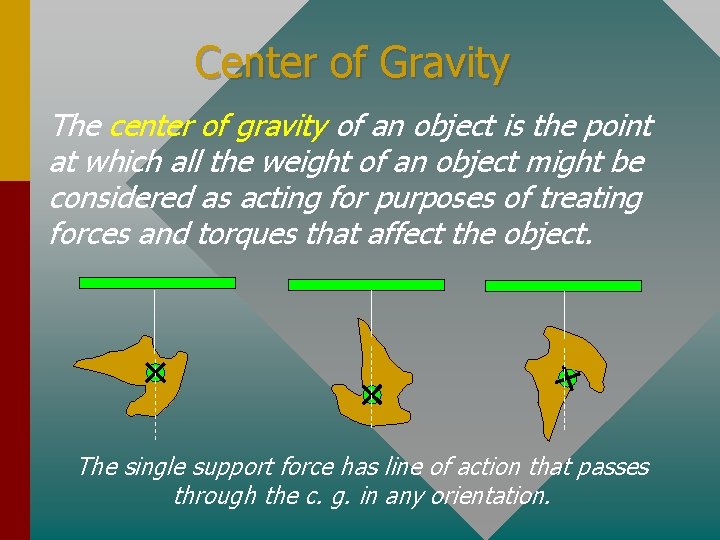
Center of Gravity The center of gravity of an object is the point at which all the weight of an object might be considered as acting for purposes of treating forces and torques that affect the object. The single support force has line of action that passes through the c. g. in any orientation.

Examples of Center of Gravity Note: C. of G. is not always inside material.

Example 5: Find the center of gravity of the apparatus shown below. Neglect the weight of the connecting rods. F C. of G. is point at which a single upupward force F will balance the system. Choose axis at left, then sum torques: St(ccw) = St(cw) Fx = (10 N)(4 m) + (5 N)(10 m) Fx = 90. 0 Nm x 4 m 30 N 6 m 10 N 5 N SF(up) = SF(down): F = 30 N + 10 N + 5 N (45 N) x = 90 N x = 2. 00 m

Summary Conditions for Equilibrium: An object is said to be in equilibrium if and only if there is no resultant force and no resultant torque.

Summary: Procedure • Draw free-body diagram and label. • Choose axis of rotation at point where least information is given. • Extend line of action forces, find moment arms, and sum torques about chosen axis: St = t 1 + t 2 + t 3 +. . . = 0 • Sum forces and set to zero: SFx= 0; SFy= 0 • Solve for unknowns.

CONCLUSION: Chapter 5 B Rotational Equilibrium