Chapter 5 AP Chemistry Gases Substances that Exist

Chapter 5 – AP Chemistry Gases

Substances that Exist as Gases at 1 atm and 25 C § Elements – – – H 2 N 2 O 2 F 2 Cl 2 He Ne Ar Kr Xe Rn § Compounds – – – HF HCl HBr HI CO CO 2 NH 3 NO NO 2 N 2 O SO 2

All Gases have the following Physical Properties § Assume the volume and shape of their containers § Are the most compressible of the states of matter § Will mix evenly and completely when confined to the same container § Have much lower densities than liquids and solids

Pressure of a Gas § Gases exert pressure on any surface with which they come into contact – Example of atmospheric pressure § The ability to drink liquid through a straw – Sucking air out of the straw reduces the pressure inside the straw – Therefore the greater atmospheric pressure on the liquid pushes it up into the straw to replace the air that has been sucked out

Atmospheric Pressure The pressure exerted by Earth’s atmosphere § Atoms and molecules are subjected to earth’s gravitational pull – Therefore, the atmosphere is much denser near the surface of the earth – The denser the air is the greater the pressure

Air § Gases are fluid – Pressure exerted on an object in a fluid comes from all directions § Air pressure at the molecular level results from collisions between air molecules and any surface with which they come into contact with § The magnitude of pressure depends on how often and how strongly the molecules impact the surface

Gas Laws § Boyle’s Law – P 1 V 1 = P 2 V 2 § Charles’s Law – V 1/T 1 = V 2/T 2 § Gay – Lussac’s Law – P 1/T 1 = P 2/T 2 § Combined Gas Law – P 1 V 1/T 1 = P 2 V 2/T 2

Combined Gas Law § A small bubble rises from the bottom of a lake, where the temperature and pressure are 8 degrees Celsius and 6. 4 atm, to the water’s surface, where the temperature is 25 degrees Celsius and pressure is 1. 0 atm. Calculate the final volume of the bubble if its initial volume was 2. 1 ml.

Ideal Gas Law § PV=n. RT – – – R =. 0821 L*atm/K*mol Volume in L Pressure in atm n in moles Temperature in Kelvin § Sulfur hexafluoride is a colorless, odorless, very unreactive gas. Calculate the pressure exerted by 84 g of the gas in a steel vessel of a volume 6. 09 L and 55 degrees Celcius.

Ideal Gas Law § Calculate the volume occupied by 14. 2 g of NH 3 at STP. (Hint 22. 4 L = 1 mol)

Gas Stoichiometry § Same a basic reaction chemistry – Please note: 1 mole = 22. 4 L can only be used when the chemical reaction is at STP – If the reaction is at STP, after moles of the unknown are calculated, then the moles can be converted to liters – If the reaction is NOT at STP then you must use ideal gas law to solve for volume

Gas Stoich Problems § Sodium Azide (Na. N 3) is used in some automobile air bags. The impact of a collision triggers the decomposition of Na. N 3. The nitrogen gas produced quickly inflates the bag between the driver and the windshield and dashboard. Calculate the volume of N 2 generated at 85 degrees Celsius and 812 mm. Hg by decomposition of 50 g Na. N 3.

Gas Stoich The breakdown on glucose is below. Calculate the volume of CO 2 produced at 37 degrees and. 5 atm when 5. 6 g of glucose is used to completion in this reaction C 6 H 12 O 6 + O 2 → CO 2 + H 2 O

Dalton’s Law of Partial Pressures § Dalton's law of partial pressures states that the total pressure exerted by a gaseous mixture is equal to the sum of the partial pressures of each individual component in a gas mixture. §

Dalton’s Law of Partial Pressure § Calculation of the moles of each gas based on the partial pressures – – For example two gases in a container (nitrogen and oxygen) P = Pnitrogen + Poxygen Then you can use ideal gas law to calculate the moles of each gas Pnitrogen V = nnitrogen R T – Poxygen V = noxygen R T § Please note you can always use the equations backwards. Start with moles of each to find partial pressures, then find the total pressure

Dalton’s Law Problems Quiz Problem § Oxygen gas is generated by the decomposition of potassium chlorate in wate vapor chamber. The volume of oxygen gas collected at 26 degrees Celsius is 752 ml and the atmospheric pressure is 1841 mm. Hg. The pressure of the water vapor at 26 degrees Celsius is 25. 2 mm. Hg. Calculate the mass of oxygen obtained.

Dalton’s Law of Partial Pressures Mole Fraction § The mole fraction that express the ratio of the number of moles of one component to the number of moles of all components present § By using mole fraction you can calculate the partial pressure of each gas in a system § P i = X i. P T § Xi -Is the percent of each molar amount of each gas (part over whole)

Dalton’s Law Problems § A mixture of gases contain 3. 85 moles of Ne, 0. 92 moles of argon and 2. 59 moles of xenon. Calulate the partial pressure of each gas if the total pressure is 2. 50 atm.

Kinetic Molecular Theory of Gases § A gas consists of a collection of small particles traveling in straight-line motion and obeying Newton's Laws. § The molecules in a gas occupy no volume (that is, they are points). § Collisions between molecules are perfectly elastic (that is, no energy is gained or lost during the collision). § There are no attractive or repulsive forces between the molecules. § The average kinetic energy of a molecule is 3 k. T/2. (T is the absolute temperature and k is the Boltzmann constant. )

Root Mean Squared § To calculate how fast a molecule moves at any given temperature R = 8. 314 J/K*mol M = (molar mass in Kg/mol) U = calculated in meters per second

Root Mean Squared Problem § Calculate the root-mean squared speeds of helium atoms and nitrogen molecules in m/s at 25 degrees Celsius
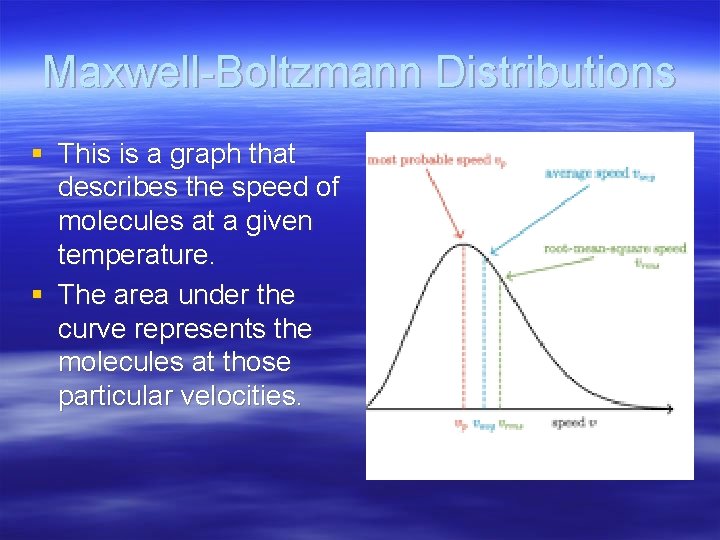
Maxwell-Boltzmann Distributions § This is a graph that describes the speed of molecules at a given temperature. § The area under the curve represents the molecules at those particular velocities.
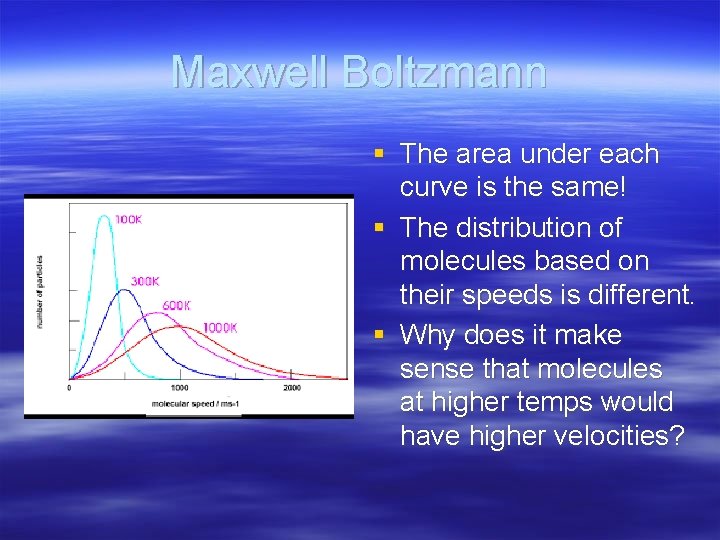
Maxwell Boltzmann § The area under each curve is the same! § The distribution of molecules based on their speeds is different. § Why does it make sense that molecules at higher temps would have higher velocities?

Gas Diffusion and Effusion § Diffusion – the gradual mixing of molecules of one gas with molecules of another by virtue of their kinetic properties § Effusion – the process by which a gas under pressure escapes from one compartment of a container to another by passing through a small opening

Graham’s law of Effusion § A flammable gas made up only of carbon and hydrogen is found to effuse through a porous barrier in 3. 5 min. Under the same conditions of temperature and pressure, it takes an equal volume of chlorine gas 7. 34 min to effuse through the same barrier. Calculate the molar mass of the unknown gas and suggest what this gas might be.

Deviation from Ideal Behavior § § § Gases deviate from ideal behavior in 2 conditions: 1) low temperature Why? At low temperature the molecules condense and become close together… Thus, IMF become too strong to ignore. 2) high pressure Why? Similarly to the first reason, at high pressure the molecules of gases are forced into a smaller volume, thus IMFs will play a role here too!

Van der Waals This is NOT going to be on the AP exam… but when intermolecular forces are present, they must be corrected for in an equation

AP Questions § 2 H 2 O 2(aq) → 2 H 2 O(l) + O 2(g) § The mass of an aqueous solution of H 2 O 2 is 6. 951 g. The H 2 O 2 in the solution decomposes completely according to the reaction represented above. The O 2(g) produced is collected in an inverted graduated tube over water at 23. 4°C and has a volume of 182. 4 m. L when the water levels inside and outside of the tube are the same. The atmospheric pressure in the lab is 762. 6 torr, and the equilibrium vapor pressure of water at 23. 4°C is 21. 6 torr. § (a) Calculate the partial pressure, in torr, of O 2(g) in the gascollection tube. § (b) Calculate the number of moles of O 2(g) produced in the reaction. § (c) Calculate the mass, in grams, of H 2 O 2 that decomposed. § (d) Calculate the percent of H 2 O 2 , by mass, in the original 6. 951 g aqueous sample.

AP Questions A rigid 5. 00 L cylinder contains 24. 5 g of N 2(g) and 28. 0 g of O 2(g) § (a) Calculate the total pressure, in atm, of the gas mixture in the cylinder at 298 K. § (b) The temperature of the gas mixture in the cylinder is decreased to 280 K. Calculate each of the following. § (i) The mole fraction of N 2(g) in the cylinder. § (ii) The partial pressure, in atm, of N 2(g) in the cylinder. § (c) If the cylinder develops a pinhole-sized leak and some of the gaseous mixture escapes, would the ratio in the cylinder increase, decrease, or remain the same? Justify your answer. A different rigid 5. 00 L cylinder contains 0. 176 mol of NO(g) at 298 K. A 0. 176 mol sample of O 2(g) is added to the cylinder, where a reaction occurs to produce NO 2(g). § (d) Write the balanced equation for the reaction. § (e) Calculate the total pressure, in atm, in the cylinder at 298 K after the reaction is complete.

AP Questions § A mixture of H 2(g), O 2(g), and 2 millilitres of H 2 O(l) is present in a 0. 500 litre rigid container at 25°C. The number of moles of H 2 and the number of moles of O 2 are equal. The total pressure is 1, 146 millimetres mercury. (The equilibrium vapor pressure of pure water at 25°C is 24 millimetres mercury. ) § The mixture is sparked, and H 2 and O 2 react until one reactant is completely consumed. § (a) Identify the reactant remaining and calculate the number of moles of the reactant remaining. § (b) Calculate the total pressure in the container at the conclusion of the reaction if the final temperature is 90°C. (The equilibrium vapor pressure of water at 90°C is 526 millimetres mercury. ) § (c) Calculate the number of moles of water present as vapor in the container at 90°C.
- Slides: 30