Chapter 5 Angle Modulation and Demodulation Part 1

Chapter 5 Angle Modulation and Demodulation Part 1

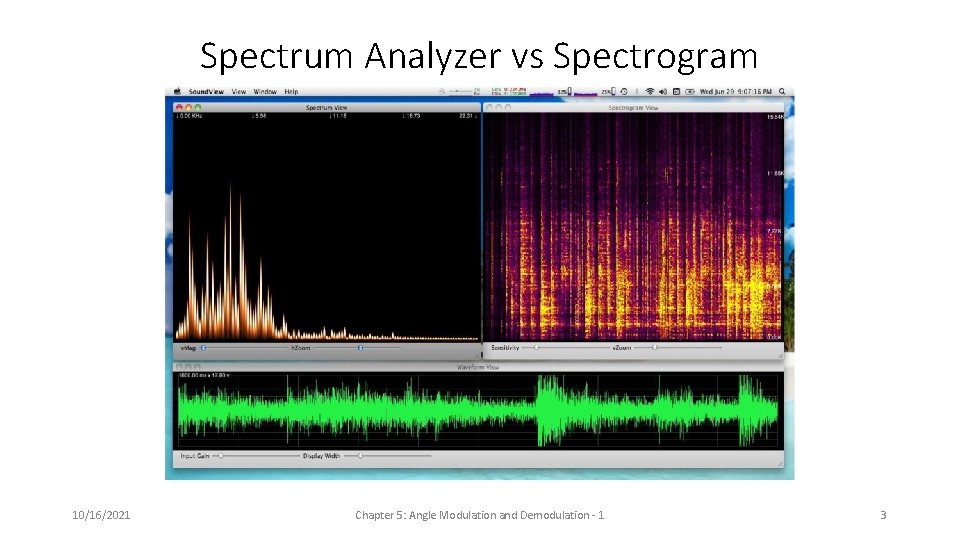
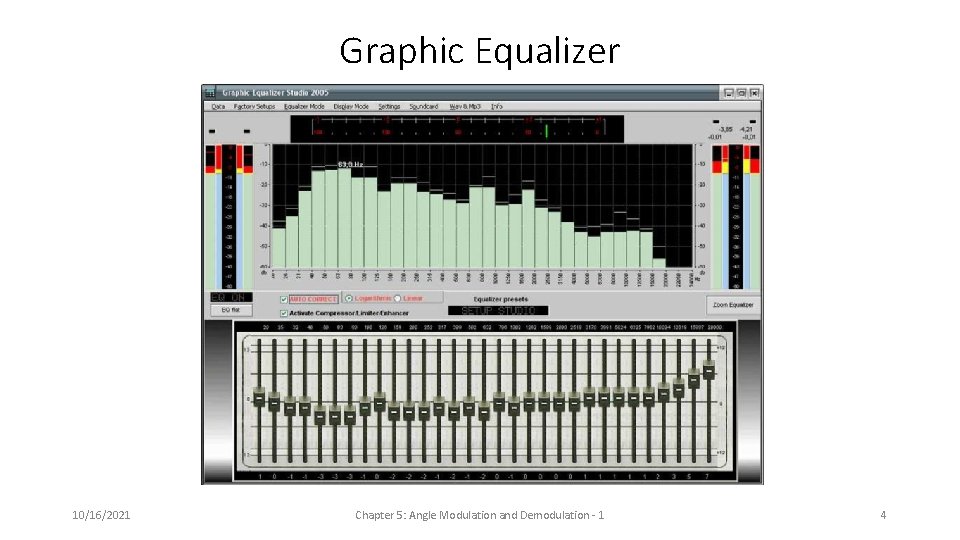
Angle Modulation • Most signals have time-varying frequency distributions (music, speech, video). • Visualizations of spectra: • Spectrogram • Spectrum analyzer • Graphics equalizer • Time-varying frequency • Instantaneous frequency • Spectra • Introduction to angle modulation • Relationship between Frequency Modulation (FM) and Phase Modulation (PM) • FM bandwidth 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 2

Spectrum Analyzer vs Spectrogram 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 3

Graphic Equalizer 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 4

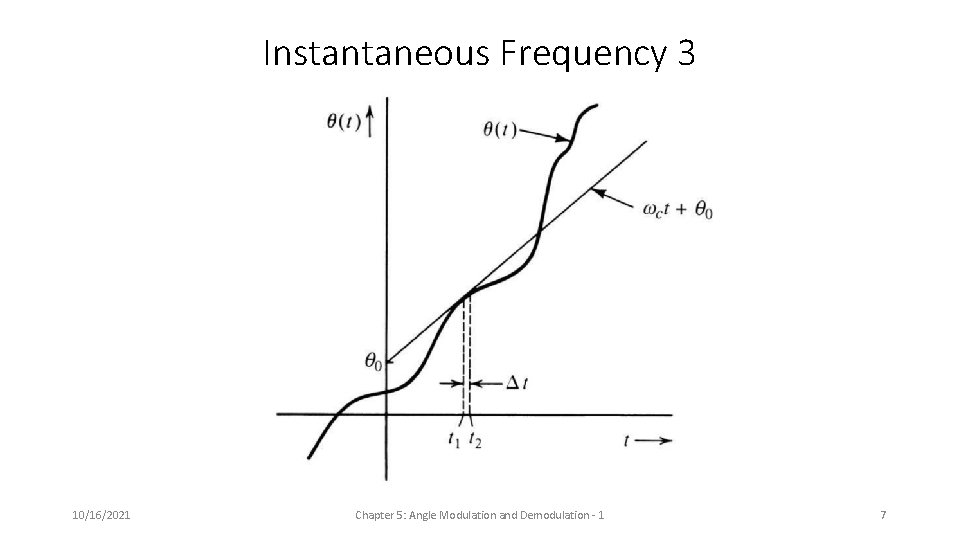
Instantaneous Frequency • In general, the frequency of a signal at an instant in time depends on the entire signal (Hilbert transform) • For generalized sinusoids, we can use a simpler approach. Suppose ϕ(t) = A cos[θ(t)] • Then θ(t) is the generalized angle. For a true sinusoid, θ(t) = ωct + θ 0 • linear with slope ωc and offset θ • The generalized angle is not limited to [0, 2π]. • Wrapping introduces discontinuities. • Mat. Lab has unwrap function to remove discontinuities. 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 5

Instantaneous Frequency 2 • Instantaneous frequency is derivative of generalized angle: • By Fundamental Theorem of Calculus, • We can modulate a generalized sinusoid by using a signal m(t) to vary either θ(t) or ωi(t). • In either case, the frequency of the modulated signal changes as a function of m(t). 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 6

Instantaneous Frequency 3 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 7

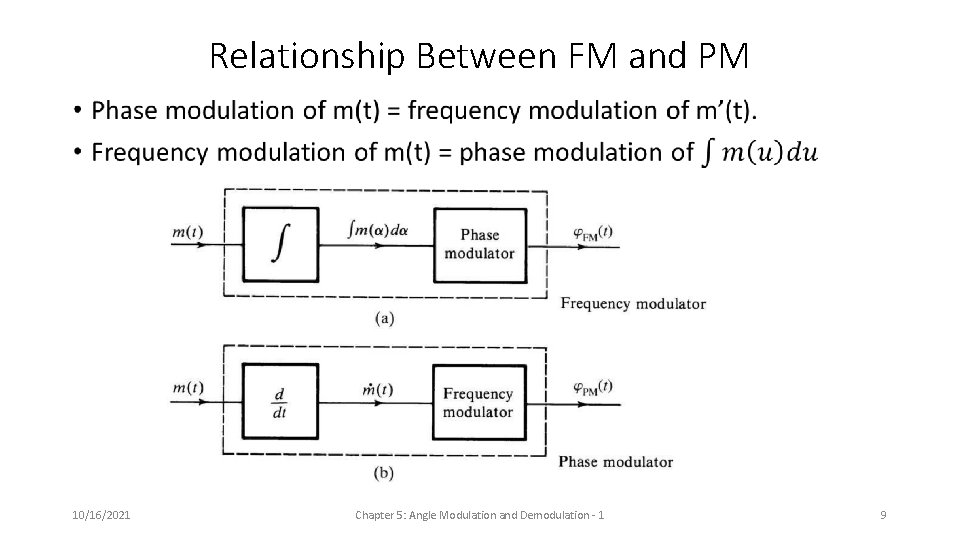
Phase Modulation (PM) & Frequency Modulation (FM) • In PM, phase is varied linearly with m(t): • The instantaneous frequency is If m(t) varies rapidly, then the frequency deviations are larger. • In FM, frequency deviation is linear in m(t): The angle is 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 8

Relationship Between FM and PM • 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 9

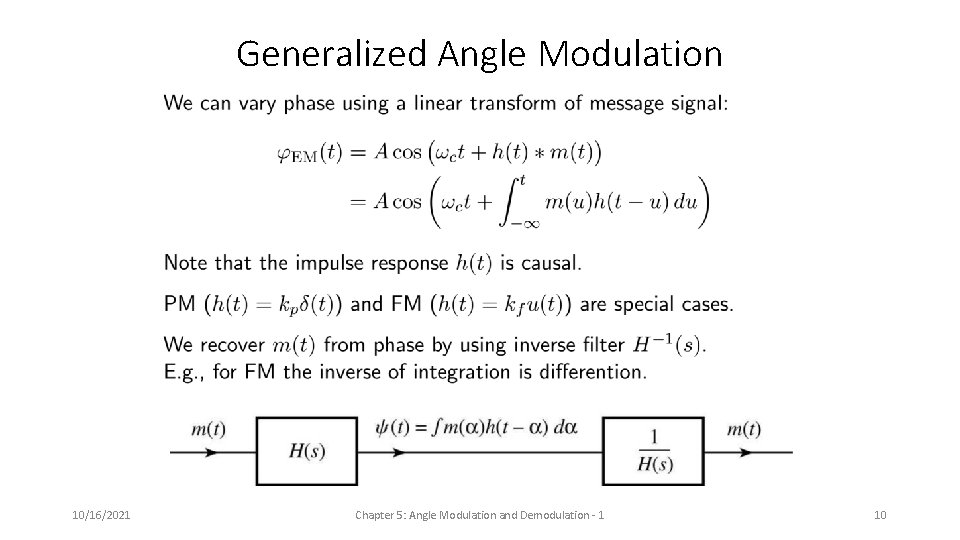
Generalized Angle Modulation 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 10

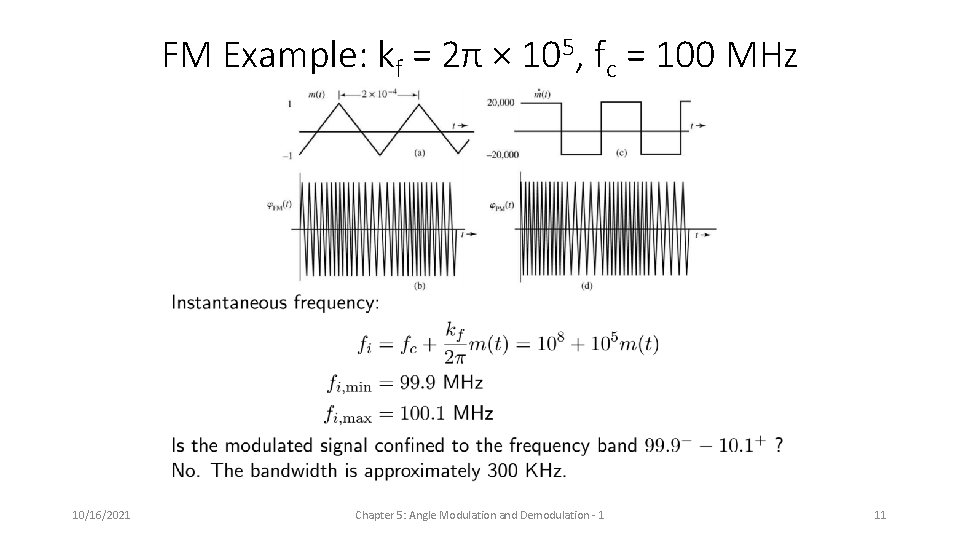
FM Example: kf = 2π × 105, fc = 100 MHz 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 11

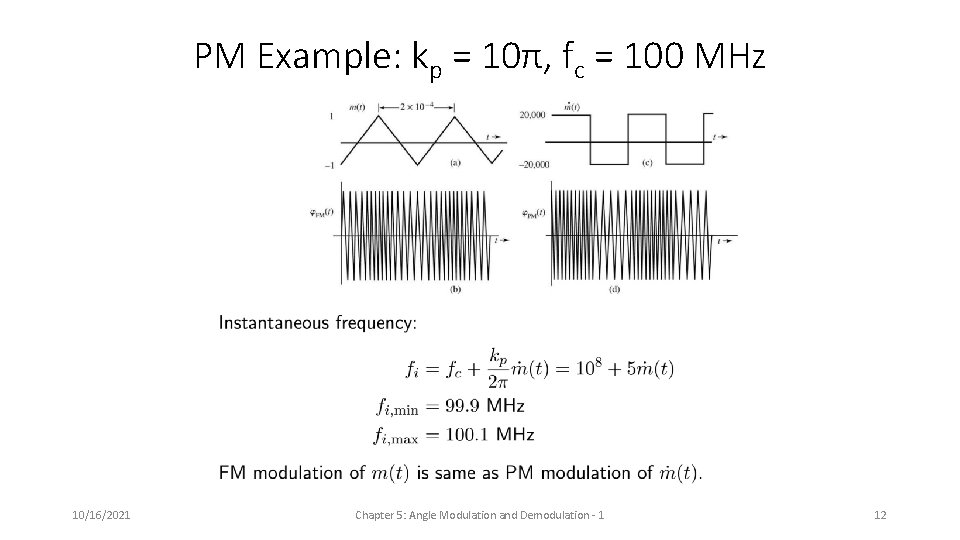
PM Example: kp = 10π, fc = 100 MHz 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 12

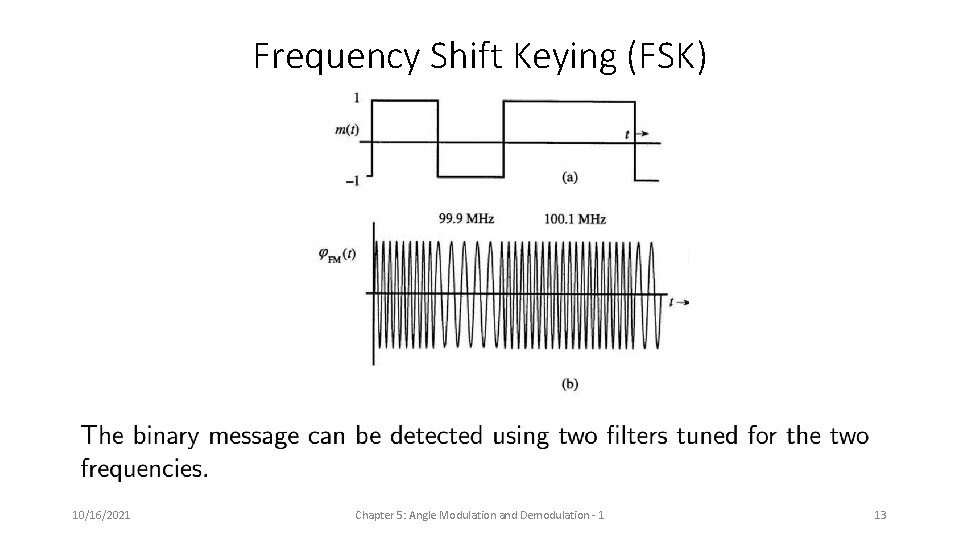
Frequency Shift Keying (FSK) 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 13

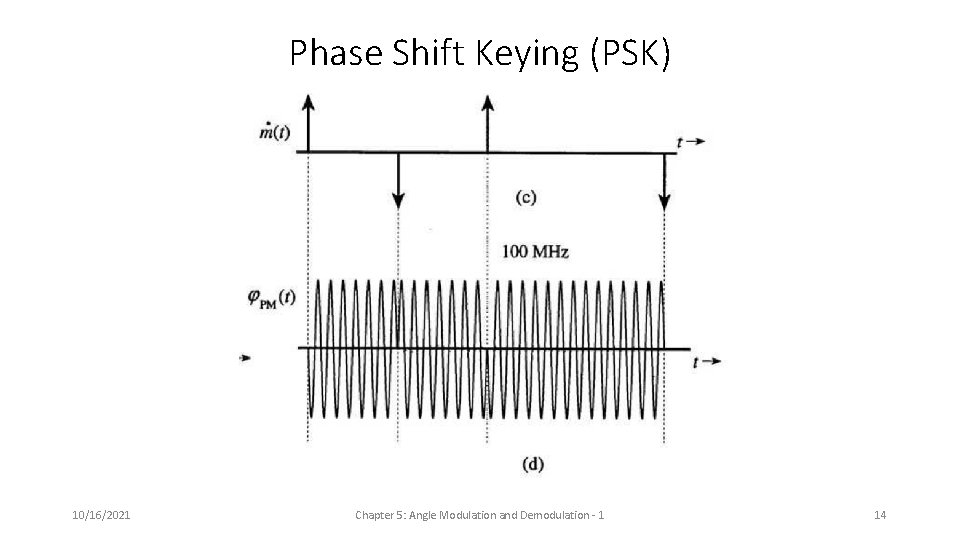
Phase Shift Keying (PSK) 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 14

PSK: Direct Modulation 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 15

Bandwidth of Angle-Modulated Waves 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 16

Narrowband FM 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 17

Narrowband FM 2 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 18

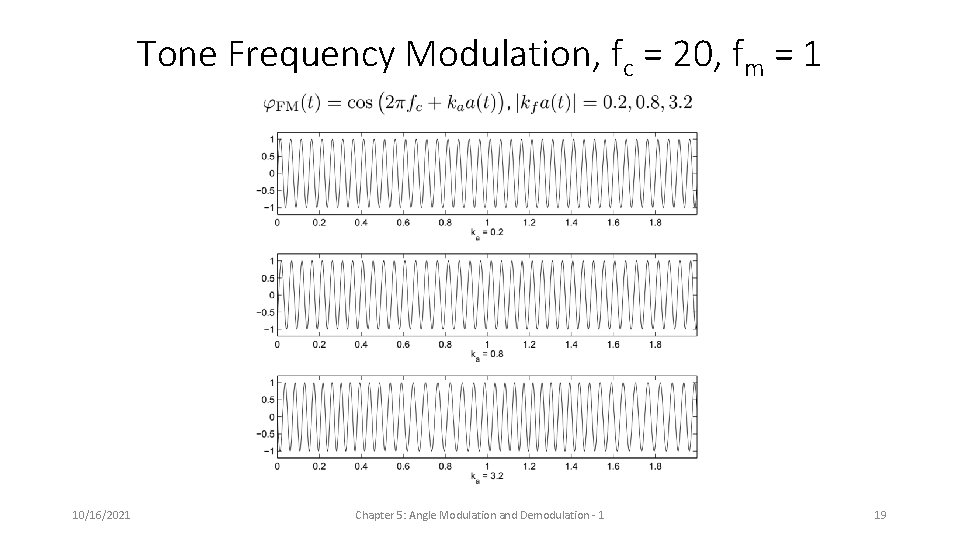
Tone Frequency Modulation, fc = 20, fm = 1 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 19

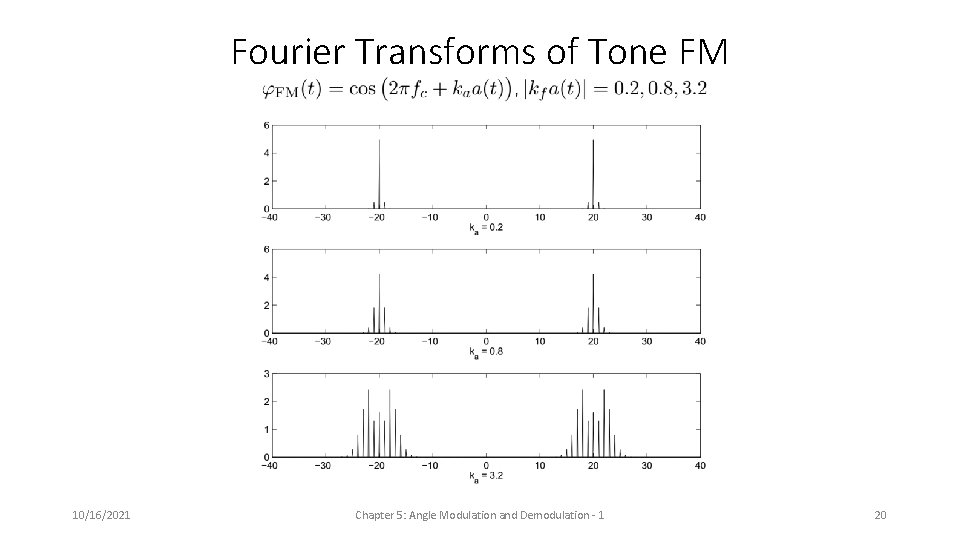
Fourier Transforms of Tone FM 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 20

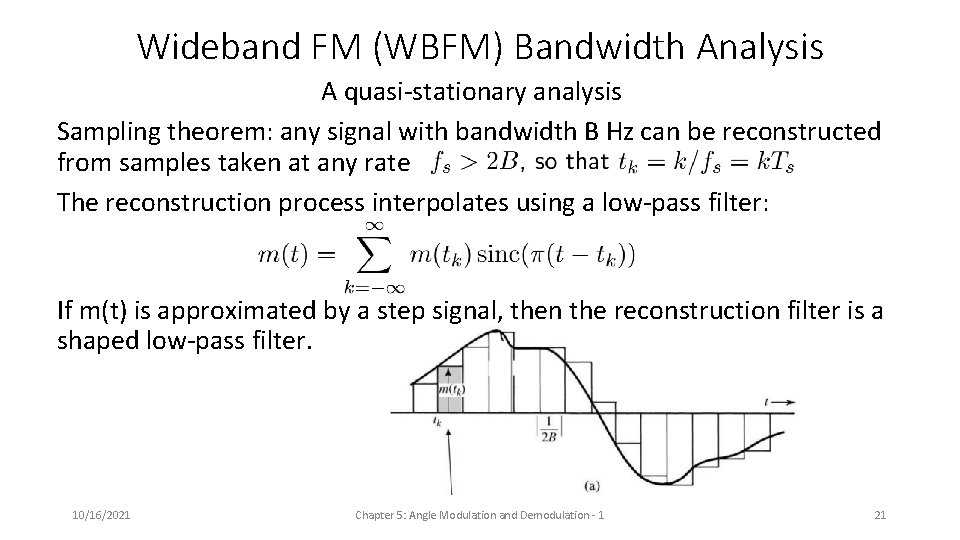
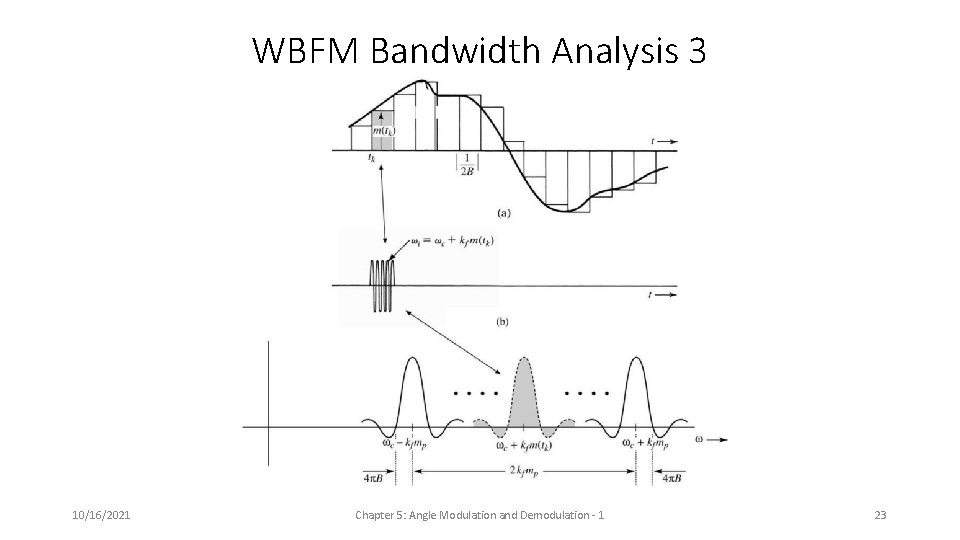
Wideband FM (WBFM) Bandwidth Analysis A quasi-stationary analysis Sampling theorem: any signal with bandwidth B Hz can be reconstructed from samples taken at any rate The reconstruction process interpolates using a low-pass filter: If m(t) is approximated by a step signal, then the reconstruction filter is a shaped low-pass filter. 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 21

WBFM Bandwidth Analysis 2 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 22

WBFM Bandwidth Analysis 3 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 23

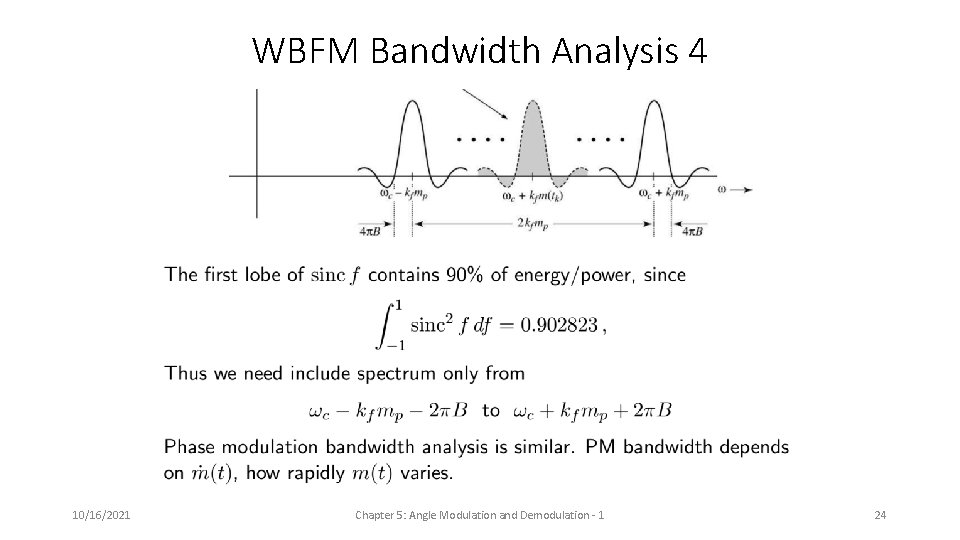
WBFM Bandwidth Analysis 4 10/16/2021 Chapter 5: Angle Modulation and Demodulation - 1 24