Chapter 5 A Exploiting the Memory Hierarchy Part

Chapter 5 A: Exploiting the Memory Hierarchy, Part 2 Read Section 5. 2: The Basics of Caches Adapted from Slides by Prof. Mary Jane Irwin, Penn State University And Slides Supplied by the textbook publisher CPE 432 Chapter 5 A. 1 Dr. W. Abu-Sufah, UJ

Cache Basics q q Two questions to deal with/answer in hardware: l Q 1: How do we know if a data item is in the cache? l Q 2: If it is, how do we find it? First we will consider “Direct Mapped” cache organization l Each memory block is mapped to exactly one block in the cache - Many of the memory blocks map into the same block in the cache l Address mapping function: Cache block # = (memory block #) modulo (# of blocks in the cache) l A tag field is associated with each cache block. The tag contains the information required to identify which memory block is resident in this cache block. CPE 432 Chapter 5 A. 2 Dr. W. Abu-Sufah, UJ

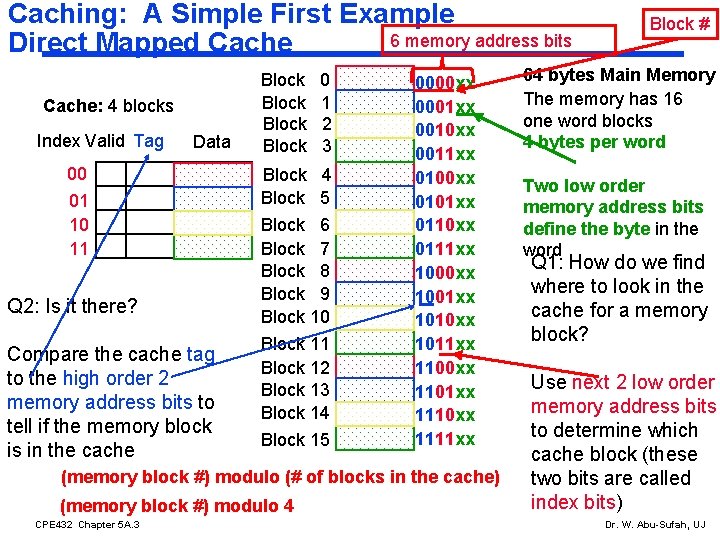
Caching: A Simple First Example 6 memory address bits Direct Mapped Cache: 4 blocks Index Valid Tag Data 00 01 10 11 Q 2: Is it there? Compare the cache tag to the high order 2 memory address bits to tell if the memory block is in the cache Block 0 1 2 3 Block 4 Block 5 Block 6 Block 7 Block 8 Block 9 Block 10 Block 11 Block 12 Block 13 Block 14 Block 15 0000 xx 0001 xx 0010 xx 0011 xx 0100 xx 0101 xx 0110 xx 0111 xx 1000 xx 1001 xx 1010 xx 1011 xx 1100 xx 1101 xx 1110 xx 1111 xx (memory block #) modulo (# of blocks in the cache) (memory block #) modulo 4 CPE 432 Chapter 5 A. 3 Block # 64 bytes Main Memory The memory has 16 one word blocks 4 bytes per word Two low order memory address bits define the byte in the word Q 1: How do we find where to look in the cache for a memory block? Use next 2 low order memory address bits to determine which cache block (these two bits are called index bits) Dr. W. Abu-Sufah, UJ

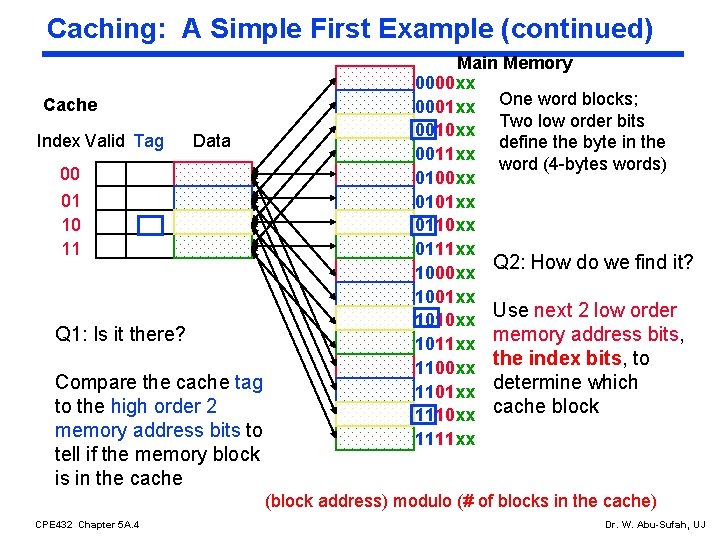
Caching: A Simple First Example (continued) Cache Index Valid Tag Data 00 01 10 11 Q 1: Is it there? Compare the cache tag to the high order 2 memory address bits to tell if the memory block is in the cache Main Memory 0000 xx 0001 xx One word blocks; Two low order bits 0010 xx define the byte in the 0011 xx word (4 -bytes words) 0100 xx 0101 xx 0110 xx 0111 xx Q 2: How do we find it? 1000 xx 1001 xx Use next 2 low order 1010 xx memory address bits, 1011 xx 1100 xx the index bits, to 1101 xx determine which 1110 xx cache block 1111 xx (block address) modulo (# of blocks in the cache) CPE 432 Chapter 5 A. 4 Dr. W. Abu-Sufah, UJ

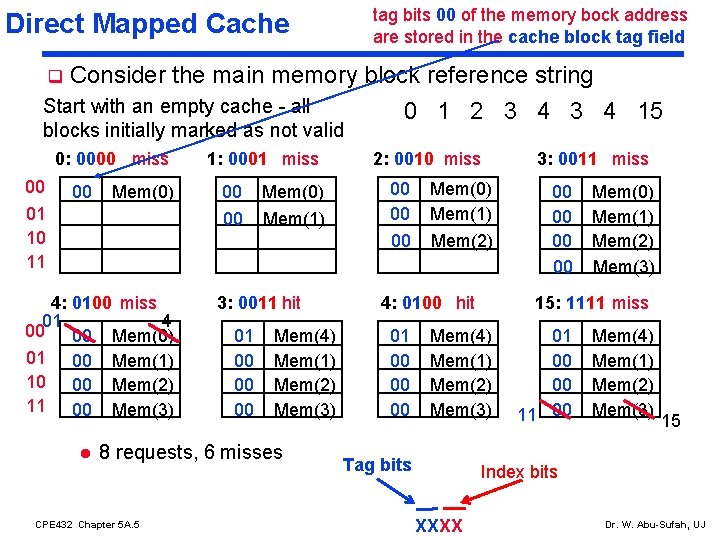
tag bits 00 of the memory bock address are stored in the cache block tag field Direct Mapped Cache q Consider the main memory block reference string Start with an empty cache - all blocks initially marked as not valid 0: 0000 miss 00 00 Mem(0) 01 10 11 4: 0100 miss 01 4 00 00 Mem(0) 01 00 Mem(1) 10 00 Mem(2) 11 00 Mem(3) l 1: 0001 miss 00 Mem(0) 00 Mem(1) 3: 0011 hit 01 00 00 00 Mem(4) Mem(1) Mem(2) Mem(3) 8 requests, 6 misses CPE 432 Chapter 5 A. 5 0 1 2 3 4 15 2: 0010 miss 00 00 00 3: 0011 miss Mem(0) Mem(1) Mem(2) 4: 0100 hit 01 00 00 00 Memory Block Address XXXX Mem(0) Mem(1) Mem(2) Mem(3) 15: 1111 miss Mem(4) Mem(1) Mem(2) Mem(3) Tag bits 00 00 01 00 00 11 00 Mem(4) Mem(1) Mem(2) Mem(3) 15 Index bits Dr. W. Abu-Sufah, UJ

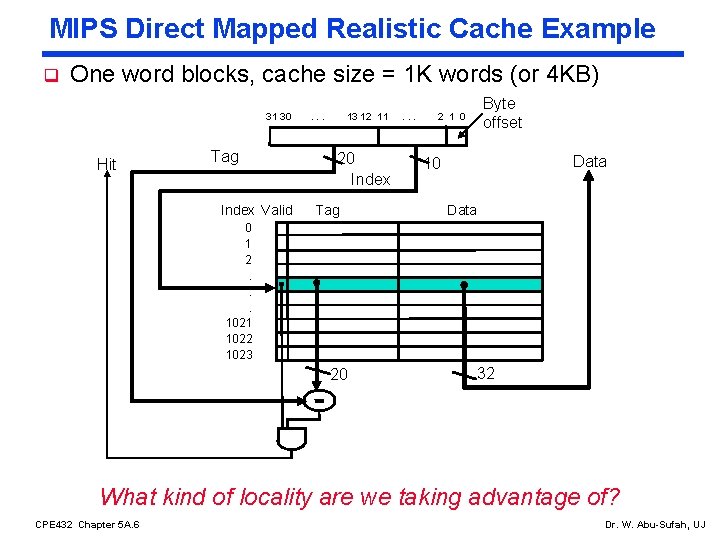
MIPS Direct Mapped Realistic Cache Example q One word blocks, cache size = 1 K words (or 4 KB) 31 30 Hit Tag Index Valid . . . 13 12 11 20 Index Tag . . . 2 1 0 Byte offset Data 10 Data 0 1 2. . . 1021 1022 1023 20 32 What kind of locality are we taking advantage of? CPE 432 Chapter 5 A. 6 Dr. W. Abu-Sufah, UJ

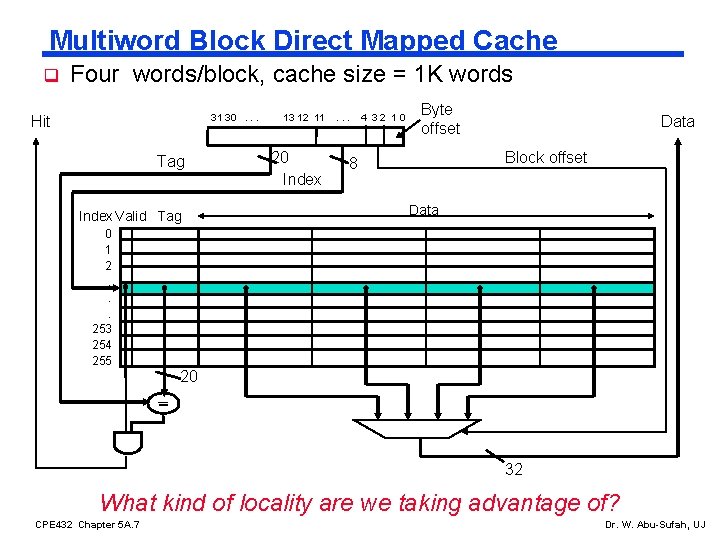
Multiword Block Direct Mapped Cache q Four words/block, cache size = 1 K words 31 30. . . Hit Tag Index Valid Tag 0 1 2. . . 253 254 255 13 12 11 20 Index . . . 4 32 10 Byte offset Data Block offset 8 Data 20 32 What kind of locality are we taking advantage of? CPE 432 Chapter 5 A. 7 Dr. W. Abu-Sufah, UJ

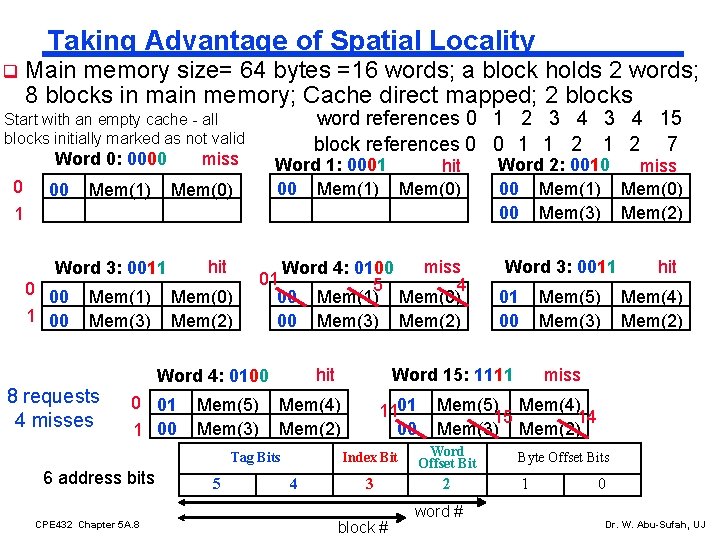
Taking Advantage of Spatial Locality q Main memory size= 64 bytes =16 words; a block holds 2 words; 8 blocks in main memory; Cache direct mapped; 2 blocks word references 0 1 2 3 4 15 block references 0 0 11 11 22 7 Start with an empty cache - all blocks initially marked as not valid Word 0: 0000 0 00 Mem(1) miss Word 1: 0001 hit 00 Mem(1) Mem(0) 1 hit Word 3: 0011 0 00 1 00 Mem(1) Mem(3) 8 requests 4 misses Mem(0) Mem(2) miss Word 4: 0100 01 5 4 00 Mem(1) Mem(0) 00 Mem(3) Mem(2) hit Word 4: 0100 0 01 1 00 Mem(5) Mem(3) 6 address bits CPE 432 Chapter 5 A. 8 5 4 Word 3: 0011 01 00 Mem(5) Mem(3) Word 15: 1111 Mem(4) Mem(2) Tag Bits Word 2: 0010 miss 00 Mem(1) Mem(0) 00 Mem(3) Mem(2) 1101 00 Mem(4) Mem(2) miss Mem(5) Mem(4) 15 14 Mem(3) Mem(2) Index Bit Word Offset Bit 3 2 block # hit word # Byte Offset Bits 1 0 Dr. W. Abu-Sufah, UJ

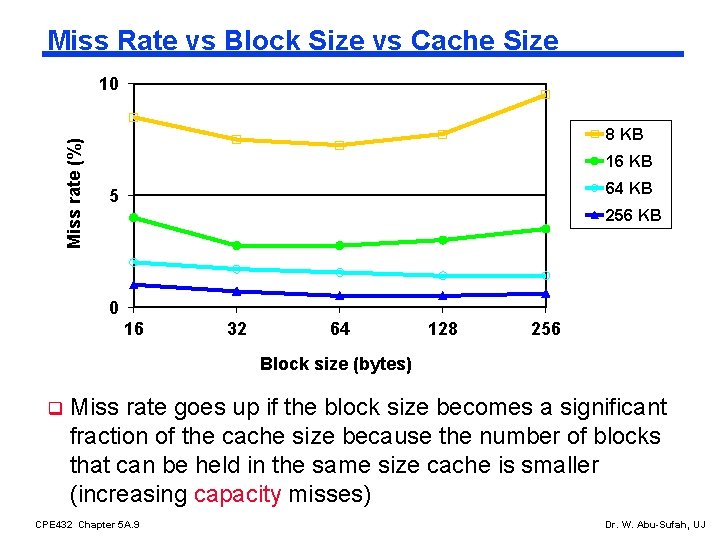
Miss Rate vs Block Size vs Cache Size Miss rate (%) 10 8 KB 16 KB 64 KB 5 256 KB 0 16 32 64 128 256 Block size (bytes) q Miss rate goes up if the block size becomes a significant fraction of the cache size because the number of blocks that can be held in the same size cache is smaller (increasing capacity misses) CPE 432 Chapter 5 A. 9 Dr. W. Abu-Sufah, UJ

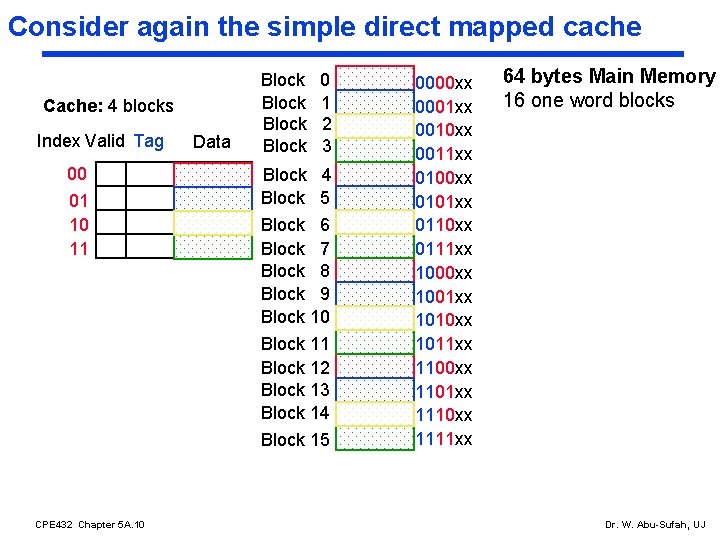
Consider again the simple direct mapped cache Cache: 4 blocks Index Valid Tag 00 01 10 11 Data Block 0 1 2 3 Block 4 Block 5 Block 6 Block 7 Block 8 Block 9 Block 10 Block 11 Block 12 Block 13 Block 14 Block 15 CPE 432 Chapter 5 A. 10 0000 xx 0001 xx 0010 xx 0011 xx 0100 xx 0101 xx 0110 xx 0111 xx 1000 xx 1001 xx 1010 xx 1011 xx 1100 xx 1101 xx 1110 xx 1111 xx 64 bytes Main Memory 16 one word blocks Dr. W. Abu-Sufah, UJ

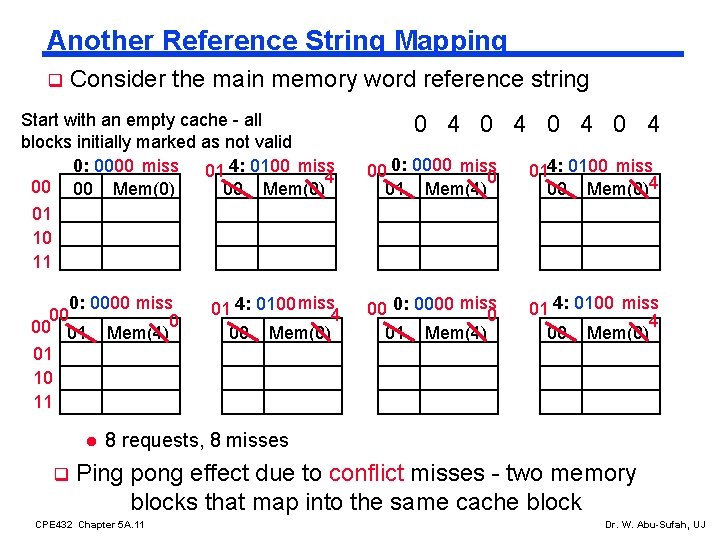
Another Reference String Mapping q Consider the main memory word reference string Start with an empty cache - all blocks initially marked as not valid 0: 0000 miss 01 4: 0100 miss 4 00 00 Mem(0) 01 10 11 0: 0000 miss 00 00 01 Mem(4)0 01 10 11 l q 01 4: 0100 miss 4 00 Mem(0) 0 4 0 4 00 0: 0000 miss 0 01 Mem(4) 014: 0100 miss 00 Mem(0)4 00 0: 0000 miss 0 01 Mem(4) 01 4: 0100 miss 4 00 Mem(0) 8 requests, 8 misses Ping pong effect due to conflict misses - two memory blocks that map into the same cache block CPE 432 Chapter 5 A. 11 Dr. W. Abu-Sufah, UJ

Reducing Cache Miss Rates: Approach #1 Allow more flexible block placement q In a direct mapped cache a memory block maps to exactly one cache block q At the other extreme, could allow a memory block to be mapped to any cache block – fully associative cache q A compromise is to divide the cache into sets each of which consists of n “ways” (n-way set associative cache). l l l A memory block maps to a unique set (specified by the index field) A memory block can be placed in any way of that set (so there are n choices) Set #= (block address) modulo (# sets in the cache) All of the tags of all of the blocks of the set must be searched for a match. CPE 432 Chapter 5 A. 12 Dr. W. Abu-Sufah, UJ

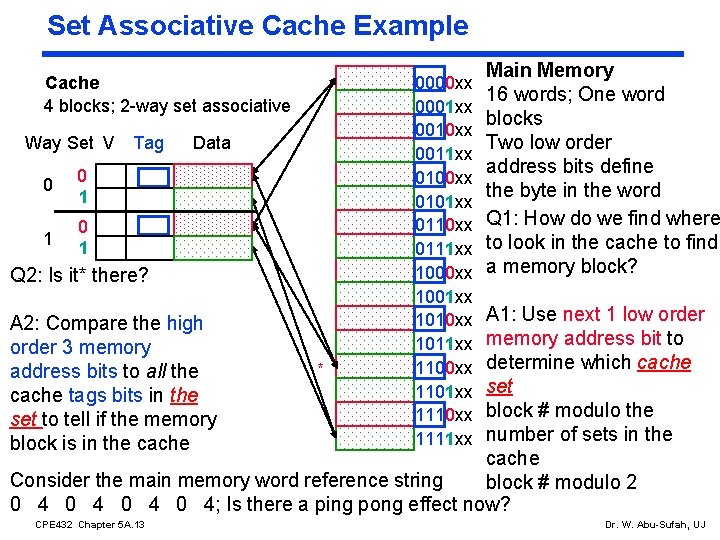
Set Associative Cache Example Cache 4 blocks; 2 -way set associative Way Set V 0 0 1 1 0 1 Tag Data Q 2: Is it* there? 0000 xx 0001 xx 0010 xx 0011 xx 0100 xx 0101 xx 0110 xx 0111 xx 1000 xx 1001 xx 1010 xx 1011 xx 1100 xx 1101 xx 1110 xx 1111 xx Main Memory 16 words; One word blocks Two low order address bits define the byte in the word Q 1: How do we find where to look in the cache to find a memory block? A 1: Use next 1 low order memory address bit to determine which cache * set block # modulo the number of sets in the cache Consider the main memory word reference string block # modulo 2 0 4 0 4; Is there a ping pong effect now? A 2: Compare the high order 3 memory address bits to all the cache tags bits in the set to tell if the memory block is in the cache CPE 432 Chapter 5 A. 13 Dr. W. Abu-Sufah, UJ

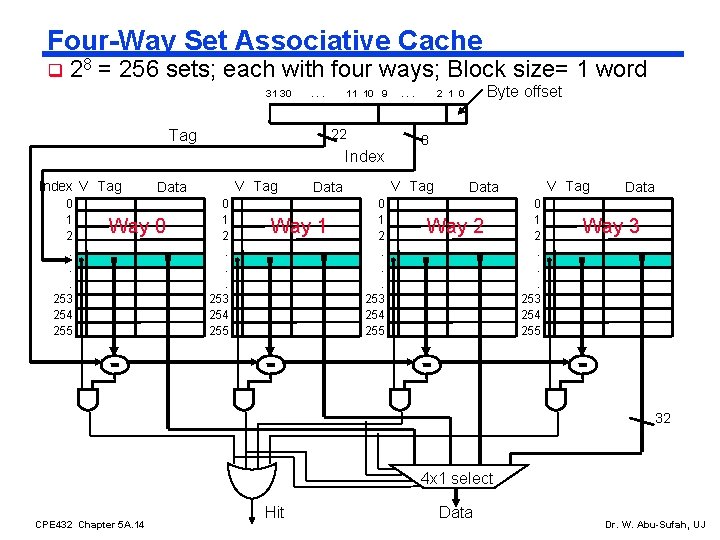
Four-Way Set Associative Cache q 28 = 256 sets; each with four ways; Block size= 1 word 31 30 . . . 11 10 9 22 Tag Index V Tag 0 1 2. . . 253 254 255 V Tag Data Way 0 0 1 2. . . 253 254 255 Byte offset 2 1 0 8 V Tag Data Way 1 . . . V Tag Data Way 2 0 1 2. . . 253 254 255 Data Way 3 32 4 x 1 select CPE 432 Chapter 5 A. 14 Hit Data Dr. W. Abu-Sufah, UJ

Range of Set Associative Caches q For a fixed size cache, each increase by a factor of two in associativity will: l double the number of blocks per set (i. e. , the number of ways) AND l halve the number of sets – decreases the size of the index by 1 bit and increases the size of the tag by 1 bit Used for tag compare Tag Decreasing associativity Direct mapped (only one way) Smaller tags, only a single comparator CPE 432 Chapter 5 A. 15 Selects the set Index Selects the word in the block Block offset Byte offset Increasing associativity Fully associative (only one set) Tag is all the bits except block and byte offset Dr. W. Abu-Sufah, UJ

Costs of Set Associative Caches q When a miss occurs, which way’s block do we pick for replacement? l Least Recently Used (LRU): the block replaced is the one that has been unused for the longest time - Must have hardware to keep track of when each way’s block was used relative to the other blocks in the set - For 2 -way set associative, takes one bit per way→ set the bit when a block is referenced (and reset the other way’s bit) CPE 432 Chapter 5 A. 16 Dr. W. Abu-Sufah, UJ

Costs of Set Associative Caches (continued) q N-way set associative cache costs l N comparators (delay and area) CPE 432 Chapter 5 A. 17 Dr. W. Abu-Sufah, UJ

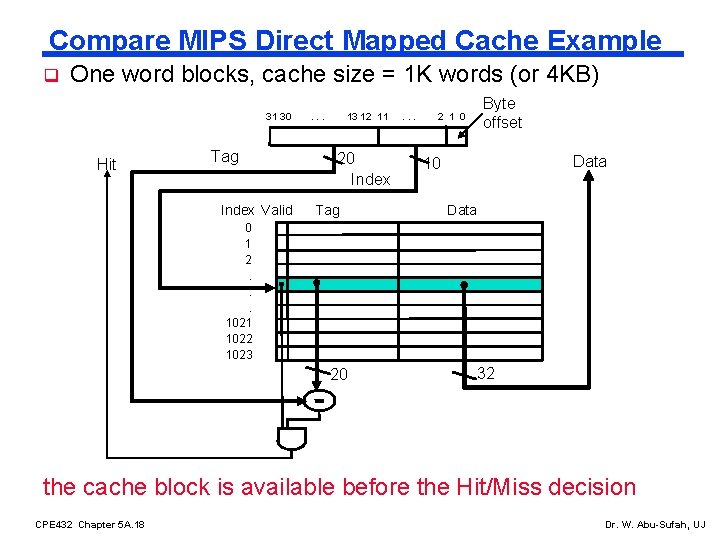
Compare MIPS Direct Mapped Cache Example q One word blocks, cache size = 1 K words (or 4 KB) 31 30 Hit Tag Index Valid . . . 13 12 11 20 Index Tag . . . 2 1 0 Byte offset Data 10 Data 0 1 2. . . 1021 1022 1023 20 32 the cache block is available before the Hit/Miss decision CPE 432 Chapter 5 A. 18 Dr. W. Abu-Sufah, UJ

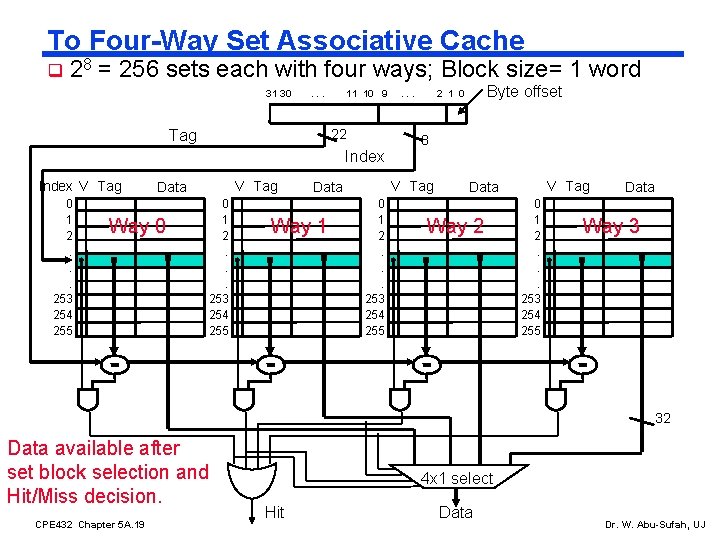
To Four-Way Set Associative Cache q 28 = 256 sets each with four ways; Block size= 1 word 31 30 . . . 11 10 9 22 Tag Index V Tag 0 1 2. . . 253 254 255 V Tag Data Way 0 0 1 2. . . 253 254 255 Byte offset 2 1 0 8 V Tag Data Way 1 . . . V Tag Data Way 2 0 1 2. . . 253 254 255 Data Way 3 32 Data available after set block selection and Hit/Miss decision. CPE 432 Chapter 5 A. 19 4 x 1 select Hit Data Dr. W. Abu-Sufah, UJ

Costs of Set Associative Caches (continued) q N-way set associative cache costs l N comparators (delay and area) l Use a MUX for selecting a block of a set before data is available - Hence a N-way set associative cache will also be slower than a direct mapped cache because of this extra multiplexer delay. l Data available after set block selection and Hit/Miss decision. In a direct mapped cache, the cache block is available before the Hit/Miss decision - So in a set associative cache it is not possible to just assume a hit and continue and recover later if it was a miss (In a direct mapped cache, this is possible) CPE 432 Chapter 5 A. 20 Dr. W. Abu-Sufah, UJ

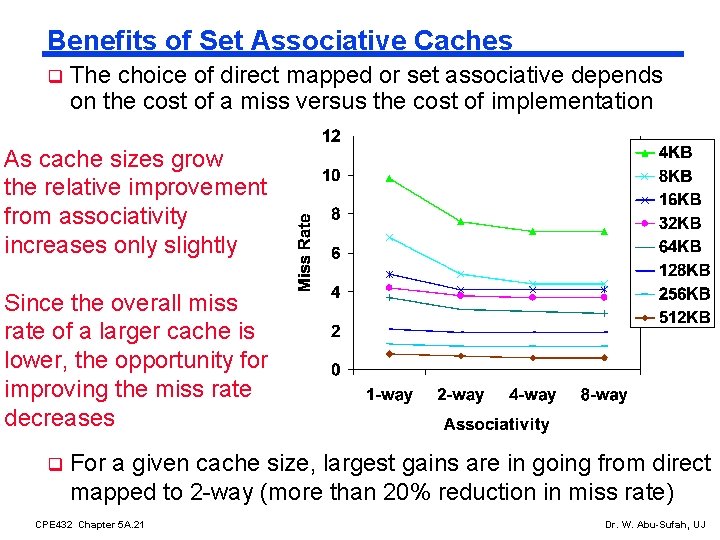
Benefits of Set Associative Caches q The choice of direct mapped or set associative depends on the cost of a miss versus the cost of implementation As cache sizes grow the relative improvement from associativity increases only slightly Since the overall miss rate of a larger cache is lower, the opportunity for improving the miss rate decreases q For a given cache size, largest gains are in going from direct mapped to 2 -way (more than 20% reduction in miss rate) CPE 432 Chapter 5 A. 21 Dr. W. Abu-Sufah, UJ