Chapter 5 1 Aristotle categorical logic According to




![Symbolizing categorical propositions • The forms show – Quantity • (“all” or “none” [universality], Symbolizing categorical propositions • The forms show – Quantity • (“all” or “none” [universality],](https://slidetodoc.com/presentation_image_h2/9d64740219a44166d444fbdace279f00/image-5.jpg)


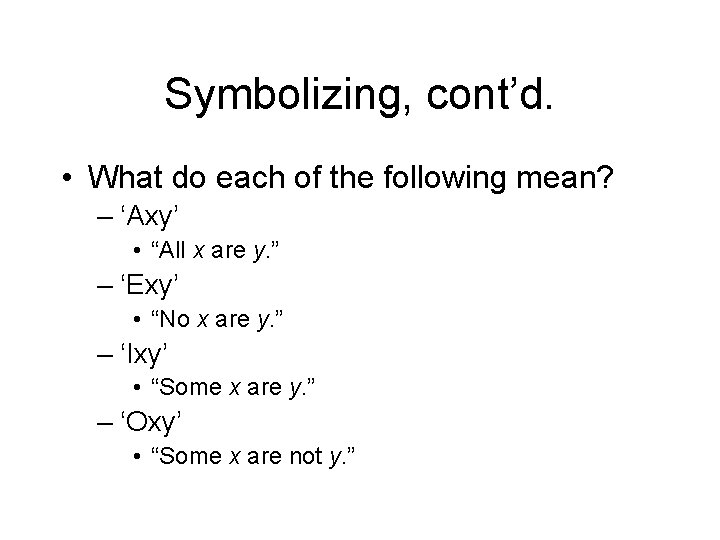




- Slides: 12

Chapter 5. 1 Aristotle & categorical logic

According to Aristotle • What is reality? – The collection of all substances • What is a substance? – A concrete, individual thing • What, then, is a statement about reality? – A truth-assessable sentence in which a substance (the subject) is identified and properties/relations (the predicate) are attributed to it, such as ‘X is y, ’ or ‘All x are y, ” etc.

According to Aristotle • What did Aristotle believe this implied for logic? – Aristotle believed all statements about reality could be rendered and assessed in this form. • (This view is not, however, shared by modern logicians, as you’ll learn in PHIL 305, if—that is—you really want to be smart. ) • Identify the subject/substance and the predicate/properties/relation of the following: – ‘Some historians of philosophy believe that Aristotle single-handedly created logic ex nihilo. ’

Symbolizing categorical propositions • Why do we need to learn symbolism? – To abstract the form and, thereby, simplify the structure of the argument, in order to evaluate it more efficiently and effectively. • There are, essentially, how many forms of categorical propositions expressing relations between two classes? – Four • What are those forms? – All x are y. No x are y. – Some x are y. Some x are not y.
![Symbolizing categorical propositions The forms show Quantity all or none universality Symbolizing categorical propositions • The forms show – Quantity • (“all” or “none” [universality],](https://slidetodoc.com/presentation_image_h2/9d64740219a44166d444fbdace279f00/image-5.jpg)
Symbolizing categorical propositions • The forms show – Quantity • (“all” or “none” [universality], and “some” [particularity]) and – quality • (positivity/affirmation or negativity/denial) • What are the names of these forms? – Universal Affirmative Universal Negative – Particular Affirmative Particular Negative • What are their abbreviations? –A E –I O

Symbolizing, cont’d. • Is there a handy demonic device for remembering these? Aff. Irmo – n. E g. O –

Content of Categorical Statements • All categorical statements have the following content in a very specific order/form: – A quantifier (specifically “all, ” “some, ” “no”) – A subject term (a class or category expressed as a noun or noun phrase) – A copula (specifically “are, ” “are not”) – A predicate term (another class or category expressed as a noun or noun phrase)
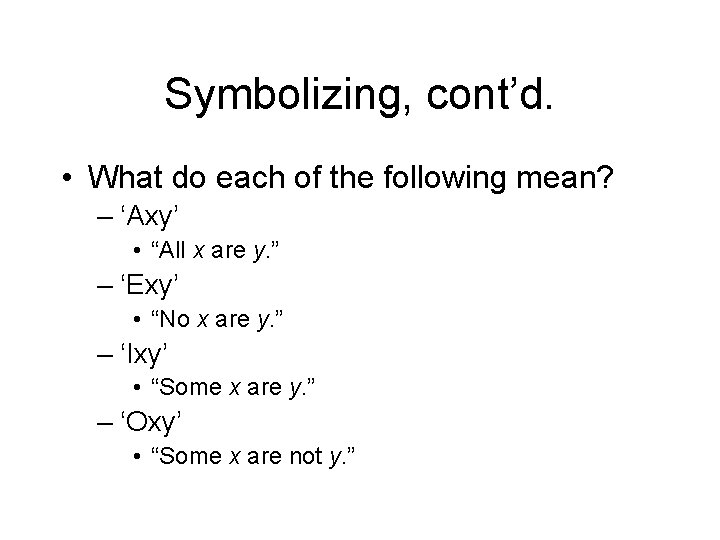
Symbolizing, cont’d. • What do each of the following mean? – ‘Axy’ • “All x are y. ” – ‘Exy’ • “No x are y. ” – ‘Ixy’ • “Some x are y. ” – ‘Oxy’ • “Some x are not y. ”

Squishy symbolism “There are no mechanical rules for translating statements from English into our logical notation. In every case one must understand the meaning of the English statement and then re-express that meaning in terms of [the logical symbols]. ” (Copi qtd. in Carter, 123)

Squishy symbolism • What effect does ‘only/only if’ have on an expression? – Identifies a necessary (consequent) condition. – It reverses the S/P order. • What effect does ‘nothing. . . unless. . . , ’ ‘nothing. . . without being. . . , ’ ‘nothing. . . but. . . , ’ ‘none but. . . , ’ etc. have? – They are translated as “All. . ” – BUT “Not any. . . ” = “none” • ‘unless, ’ ‘until, ’ ‘except, ’ ‘without’ = make necessary (apodasis/’then’ part), & negate sufficient (prodasis/’if part’) – “We will not go unless you clean your room” = “If we go, then you [will have] cleaned your room. ”

Squishy symbolism • Pay attention to context, be sensitive, use good judgment. • Answers may vary, to some degree. • Translation takes practice, experience, and years of self-denial and selfmastery. • Study carefully the summary of stylistic variants in Chapter 5. 1
