Chapter 42 Standard Forms of Boolean Expressions Standard

Chapter 4_2 Standard Forms of Boolean Expressions

Standard Forms of Boolean Expression Two standard forms Sum-of-products (SOP) form Product-of-sums (POS) form Standardization Evaluation, simplification and implementation of boolean expressions become more systematic, easy

SOP Form Product term : a term that consists of the product (Boolean multiplication) of literals (variables or their complements). Sum-of-products (SOP) : sum of two or more product terms Example : AB + ABC literal Product term Sum-of-products

SOP Form SOP can contain single variable term; > A + BC + ABC A single overbar cannot extend over more than one variable, although more than one variable in a term can have an overbar; > A B C but not ABC

Domain of a Boolean Expression Domain : set of variables contained in the expression in either complemented or uncomplemented form. Example: AB+ABC Domain: A, B, C ABC+CDE+BCD Domain: A, B, C, D, E

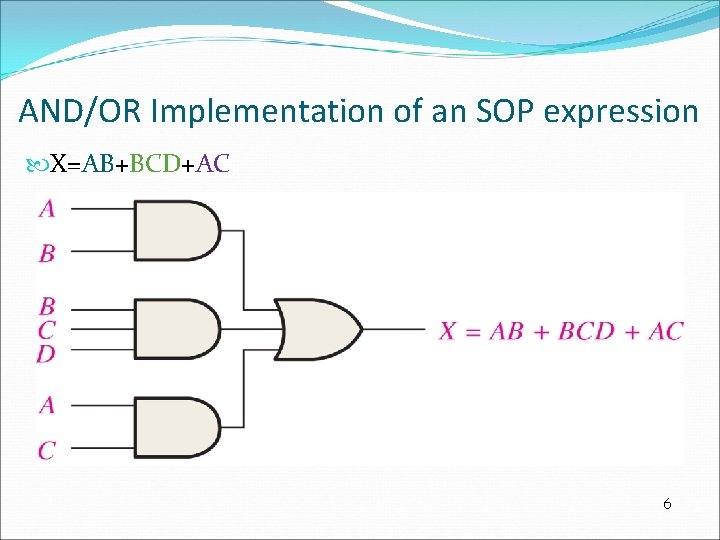
AND/OR Implementation of an SOP expression X=AB+BCD+AC 6

Conversion of a General Expression to SOP Form Any logic expression can be change into SOP form by applying Boolean Algebra techniques Example: Try This:

Conversion of a General Expression to SOP Form Convert each of the Boolean expression to SOP form:

The Standard SOP Form SOP expressions ABC + ABD + ABCD Domain: ? ? A, B, C, D • Standard SOP expression—an expression where all the variables in the domain appear in each of its product term in the expression. • Important in: - Constructing truth tables - Karnaugh Map simplification method

Conversion of a SOP expression to Standard SOP expression A non-standard SOP expression is converted into standard form using Boolean Algebra Rule 6 ( A + A = 1) Example: A + B Step 1 : Multiply each non-standard product term by 1. A+B = A· 1 + B Step 2: Replace 1 by the sum of a missing variable and its complement = A·(B+B) + B = AB + B Step 3: Repeat Steps 1, 2 until all product terms contain all variables in the domain

Conversion of a SOP expression to Standard SOP expression A+B = A· 1 + B = A·(B+B) + B = AB + B =AB + B· 1 =AB + B(A+A) =AB +AB A+B= AB + AB Example 2 : • ABC + ABCD

The Products-of-Sum (POS) Form Sum term : a term that consists of the sum of literals (variables or their complements). Product-of-sums : multiplication of two or more sum terms Example:

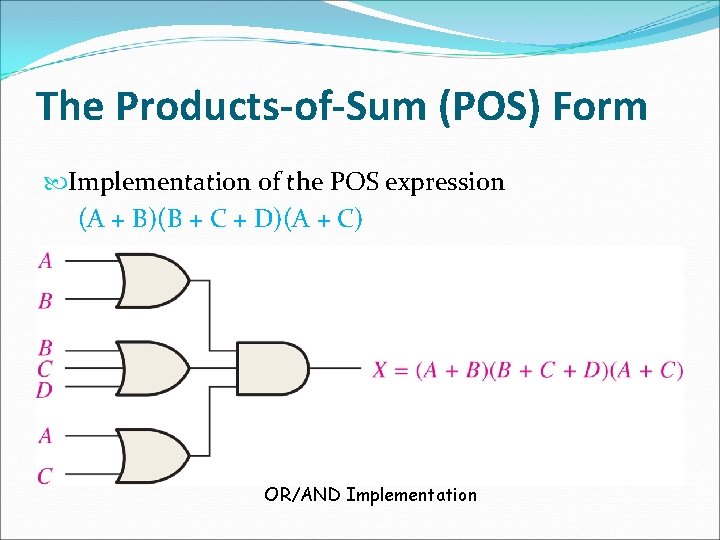
The Products-of-Sum (POS) Form Implementation of the POS expression (A + B)(B + C + D)(A + C) OR/AND Implementation

Standard POS Expression An expression where all of the variables in the domain appear in each of its sum term in the expression. A nonstandard POS expression is converted into standard form using Boolean algebra Rule 8 ( A. A = 0)

Conversion of a POS expression to Standard POS expression Step 1: Add to each nonstandard product term 0. Step 2: Replace 0 by a product of a missing variable and its complement. ( A. A = 0) Step 3: Apply rule 12: A+BC=(A+B)(A+C) Step 4: Repeat Steps 1, 2, 3 until each product term contains all variables in the domain.

Conversion of a POS expression to Standard POS expression Rule 12!

Binary Representation Sum-of-Products (SOP) An SOP expression is equal to 1 only if one or more of its product terms is equal to 1. ABCD = 1. 0 = 1. 1 = 1 Product-of-Sums (POS) - A POS expression is equal to 0 only if one or more of its sum terms is equal to 0. A+B+C+D = 0 + 1+ 0 + 1 = 0 + 0 +0

Converting Standard SOP to Standard POS Step 1: For each product term of the SOP expression, determine the binary number that represent the product term. Step 2: Determine all the binary numbers not obtained in Step 1. Step 3: Write the equivalent sum term for each binary number obtained in Step 2. - Use similar procedure to convert POS to SOP 19

Converting Standard SOP to Standard POS Example: Express them in POS form • A B C + A BC Step 1: Since there are 3 variables , there are total of 8 possible combination -> 23 = 8 Binary number : 000 + 011 + 101 + 111( sum term = 1) Step 2 : Step 3: Binary not obtained: 001, 100 , 110 ( sum term = 0 ) Equivalent binary expression obtained in step 2: ( A + B+ C )(A + B + C )( A + B + C ) These are the POS expression.

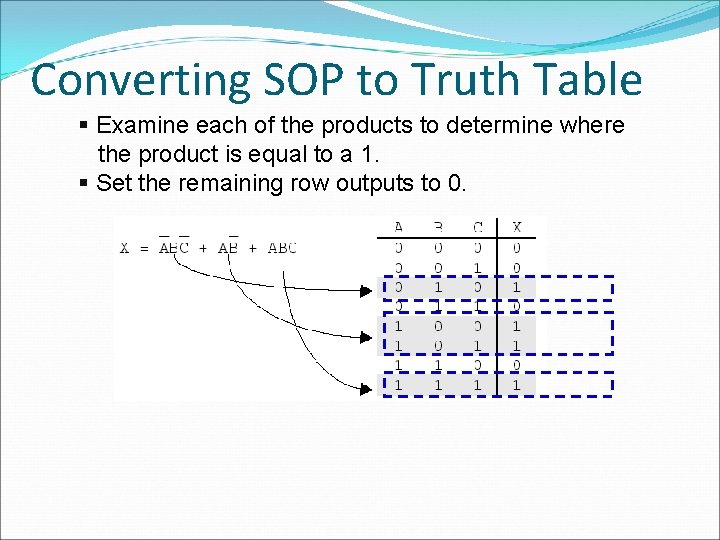
Converting SOP to Truth Table § Examine each of the products to determine where the product is equal to a 1. § Set the remaining row outputs to 0.

Converting POS to Truth Table § Opposite process from the SOP expressions. § Each sum term results in a 0. § Set the remaining row outputs to 1.

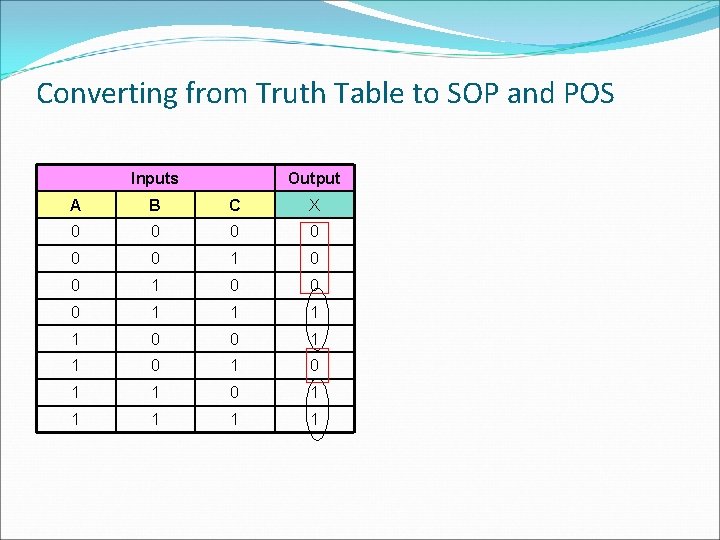
Converting from Truth Table to SOP and POS Inputs Output A B C X 0 0 0 1 1 0 0 1 1 1