Chapter 40 QUANTUM MECHANICS SCHRDINGER EQUATION The timeindependent

Chapter 40 QUANTUM MECHANICS

SCHRÖDINGER EQUATION The (time-independent) Schrödinger equation of a particle of mass m in a potential energy well V(x) is given by: The complex function ψ is called the wave function. It determines the probability of all experimental outcomes. A wave function must be a continuous function.

COMPLEX CONJUGATE

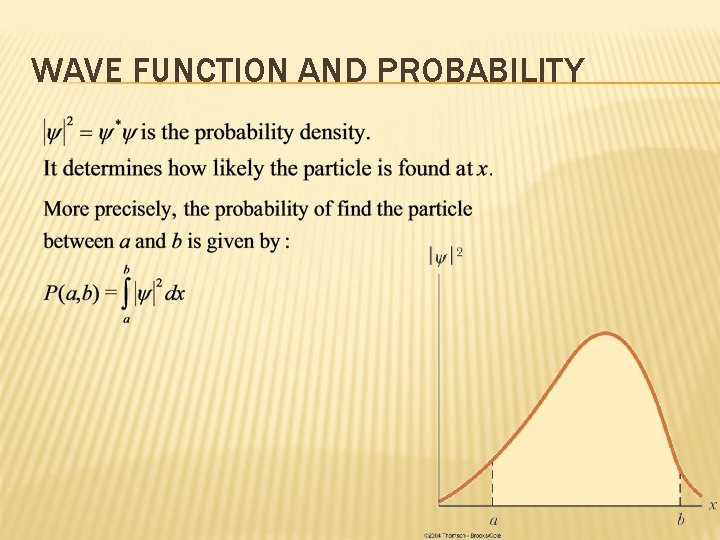
WAVE FUNCTION AND PROBABILITY

NORMALIZATION CONDITION

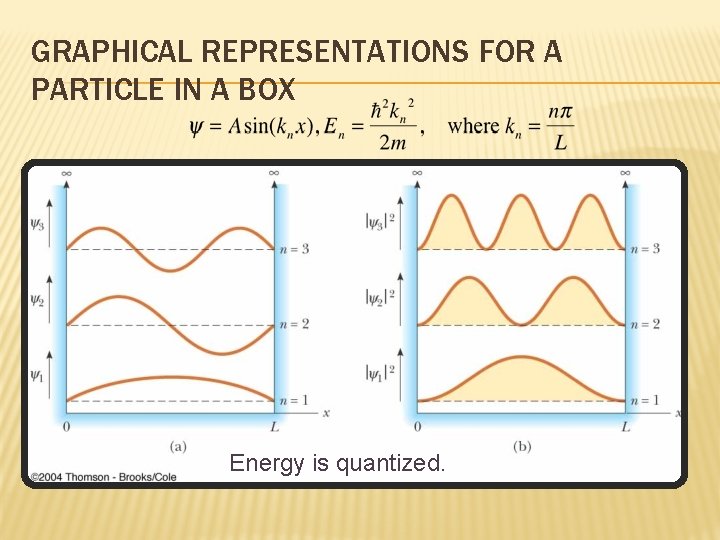
POTENTIAL ENERGY FOR A PARTICLE IN A BOX The picture on the right represents the potential energy V(x) of a “box” (or a square well). A particle inside the box cannot go beyond 0 and L because of the infinitely high energy. Solution to the Schrödinger equation gives:

DERIVATION OF THE WAVE FUNCTION

CONTINUITY OF WAVE FUNCTION

GRAPHICAL REPRESENTATIONS FOR A PARTICLE IN A BOX Energy is quantized.

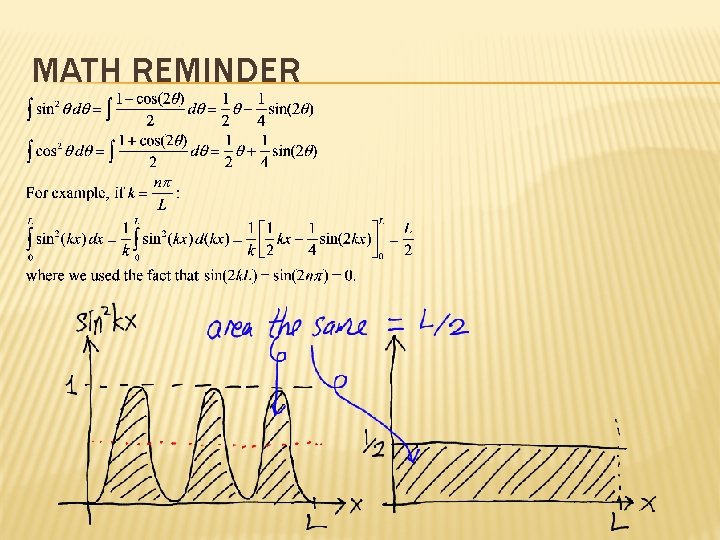
MATH REMINDER

FIND THE NORMALIZATION CONSTANT

OPERATOR CORRESPONDENCE In quantum mechanics, for every possible physical measurement (observation) you can make, there is a corresponding operator that you can use to make predictions. We will discuss how in the next slide, but here are some examples of the operators: Measurement Position Momentum in the x-direction Energy Angular momentum in the zdirection Operator

MEASUREMENT AND EXPECTATION VALUE According to quantum mechanics, in general you cannot predict the outcome of a particular experimental measurement. However, if you do the same measurement over many identically prepared system, you can make a prediction about the expectation value (average) of the measurement.

MATH REMINDER

MEASUREMENTS MUST BE REAL All physical measurements we perform in the lab must give real numbers as outcome (as opposed to complex numbers), so our expectation values must also be real. This is, however, not obvious in quantum mechanics because everything are written in complex numbers. Here is an example using momentum operator to show we will always get real numbers in the end:

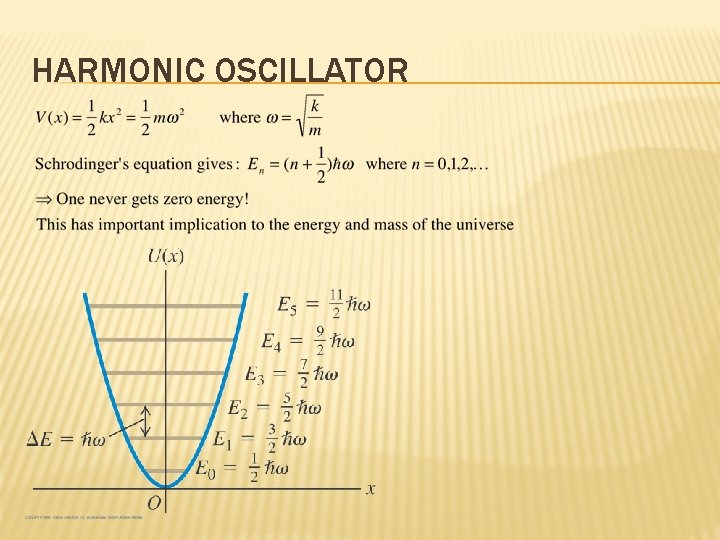
HARMONIC OSCILLATOR

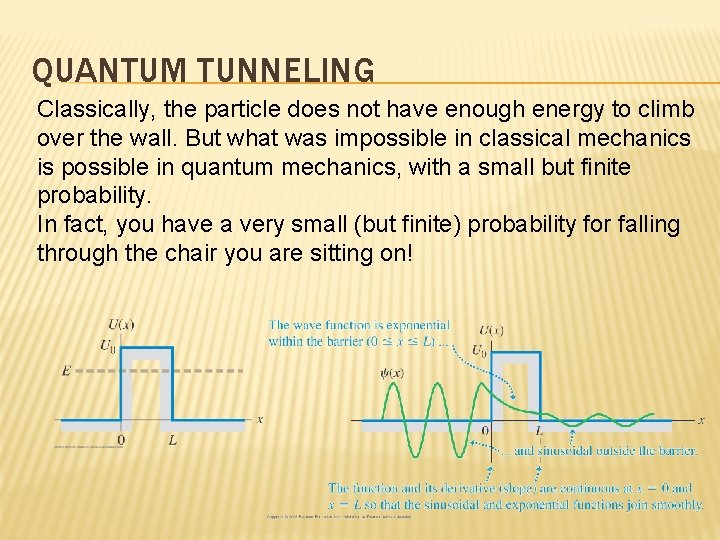
QUANTUM TUNNELING Classically, the particle does not have enough energy to climb over the wall. But what was impossible in classical mechanics is possible in quantum mechanics, with a small but finite probability. In fact, you have a very small (but finite) probability for falling through the chair you are sitting on!

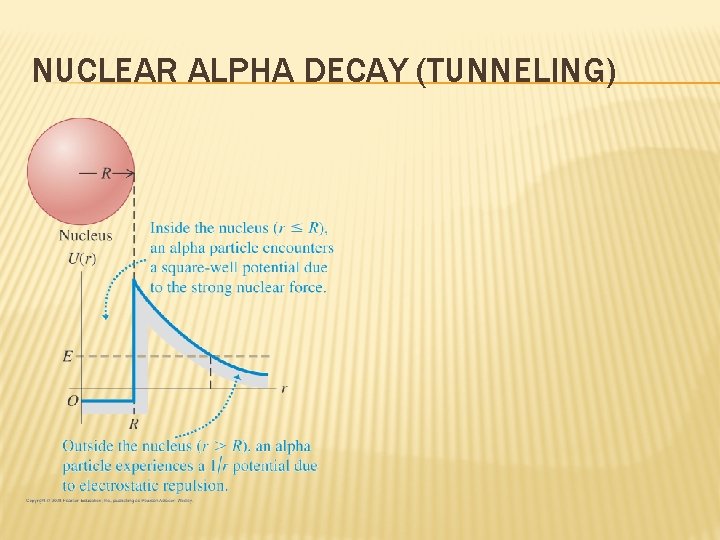
NUCLEAR ALPHA DECAY (TUNNELING)