Chapter 4 Utility Key Concept Utility an indicator


















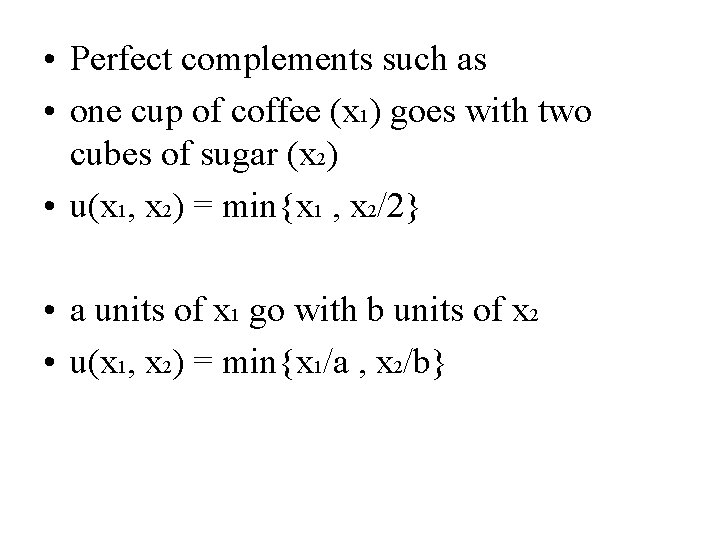

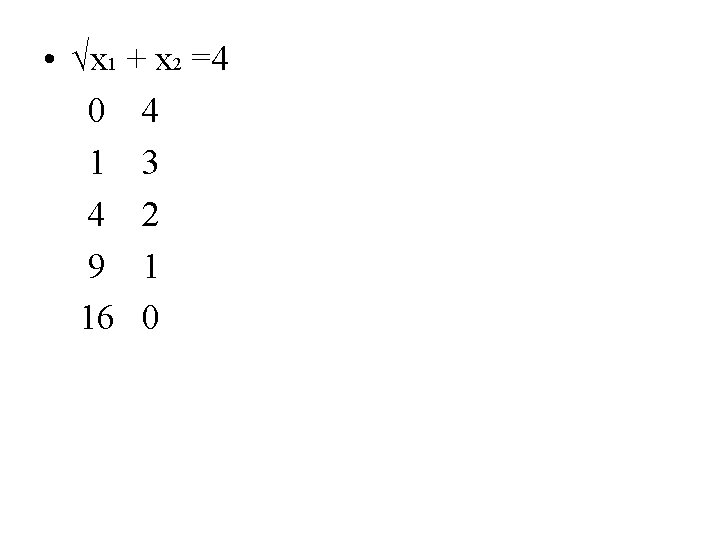









- Slides: 38

• Chapter 4 Utility • Key Concept: Utility, an indicator of a person’s overall well-being • We only use its ordinal property. • MRS does not depends on the utility function used. • MRS 1, 2= ∆x 2/ ∆x 1= -MU 1 / MU 2

• Chapter 4 Utility • Utility is an numeric measure of a person’s happiness.

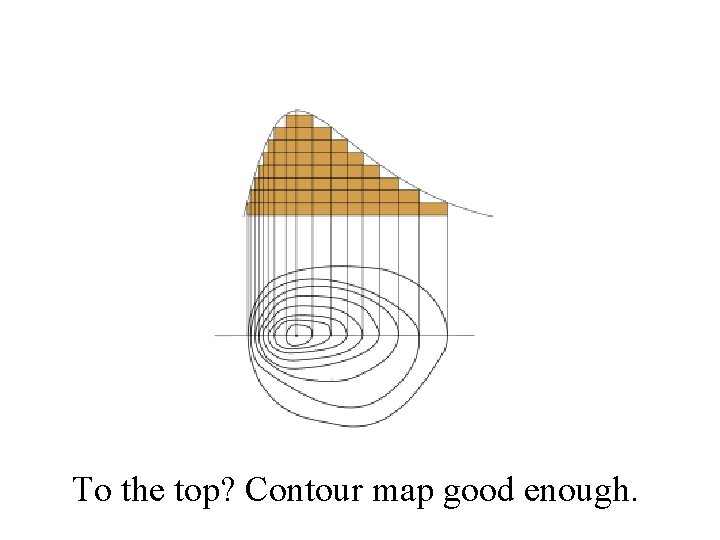
To the top? Contour map good enough.


• How do we quantify? • What does it mean by “A gives twice as much utility as B? ” • Is one person’s utility the same as another’s?

• Any independent meaning except that it is something that people maximize?

• We now use utility as a way to describe preferences. • Preferences are enough.

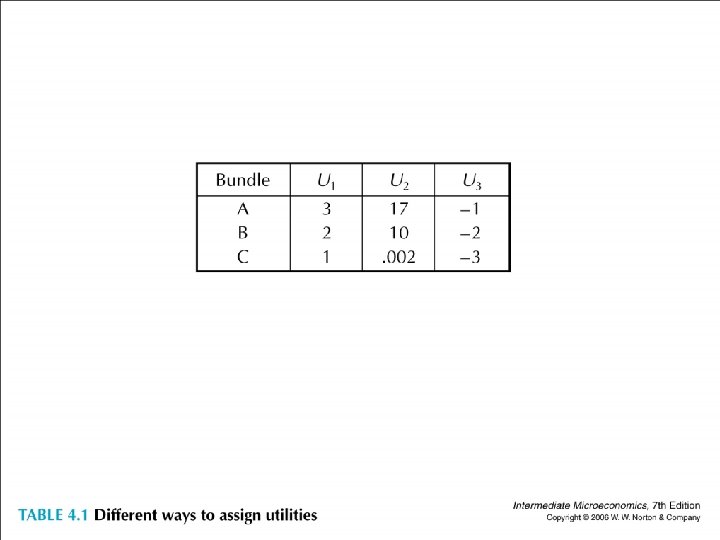
• Utility function: a way of assigning number to every possible consumption bundle such that more-preferred bundles get assigned larger numbers than lesspreferred bundles, • i. e. (x 1, x 2) w (y 1, y 2) iff u(x 1, x 2) ≥ u (y 1, y 2)

• Ordinal utility (序數) vs Cardinal utility ( 基數) • Ordinal number (序數): tells the position of something in the list, 1 st, 2 nd, 3 • Cardinal number (基數) : how many of something there are, 1, 2, 3

• Ordinal utility (序數): • ordering important • the size of the difference unimportant • v(x 1, x 2) = 2 u(x 1, x 2), u and v are equally good because • v(x 1, x 2) ≥ v(y 1, y 2) iff u(x 1, x 2) ≥ u (y 1, y 2)

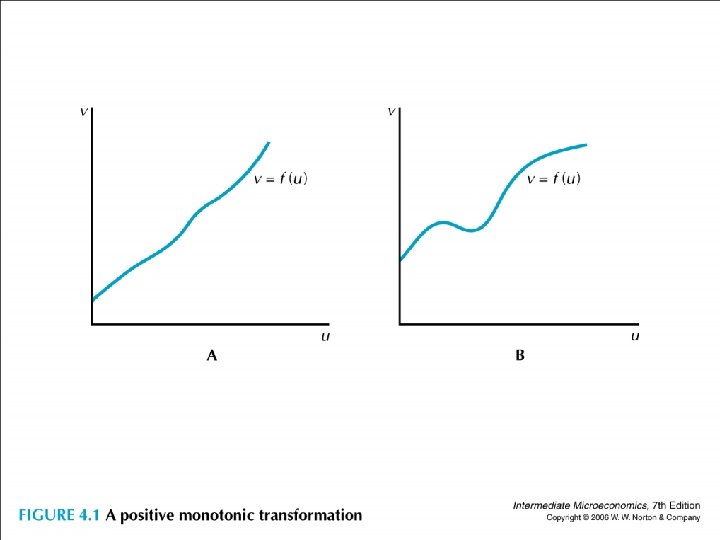
• Multiplication by 2 is an example of monotonic transformation. • It is a way to transform one set of numbers into another set such that the order is preserved.


• Suppose v is a monotonic transformation of u. • Because the order is preserved, if we plot v vs. u, then the slope is strictly positive.


• The utility function representing a preference is not unique as we can always do a monotonic transformation.

• Cardinal utility (基數): the magnitude of utility matters. • Where are we sensitive? At regions that we often have to make decisions.

• a remote Australian aboriginal tongue, Guugu Yimithirr, from north Queensland • cardinal directions (geographic languages) vs egocentric coordinates

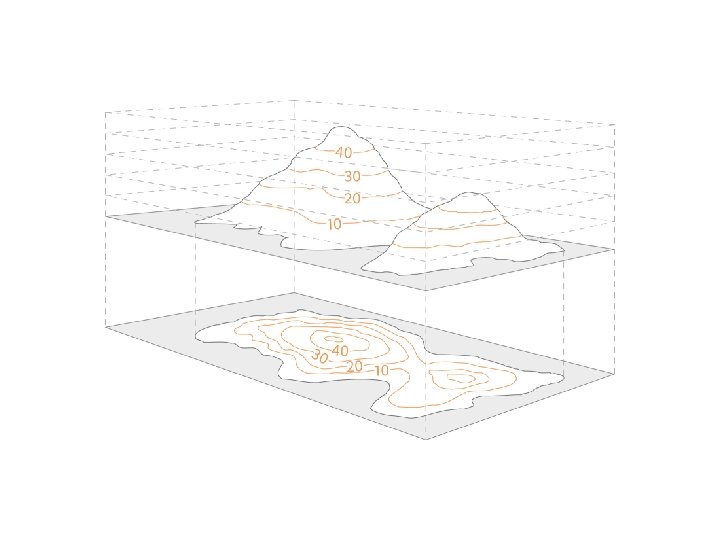
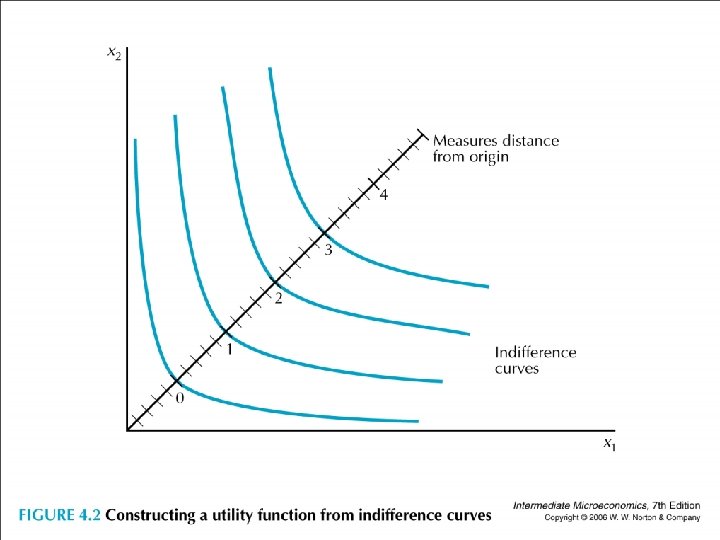
• A utility function is a way to label indifference curve. • One natural way to construct a utility function is to drawing a diagonal line and measure how far each indifference curve is from the origin


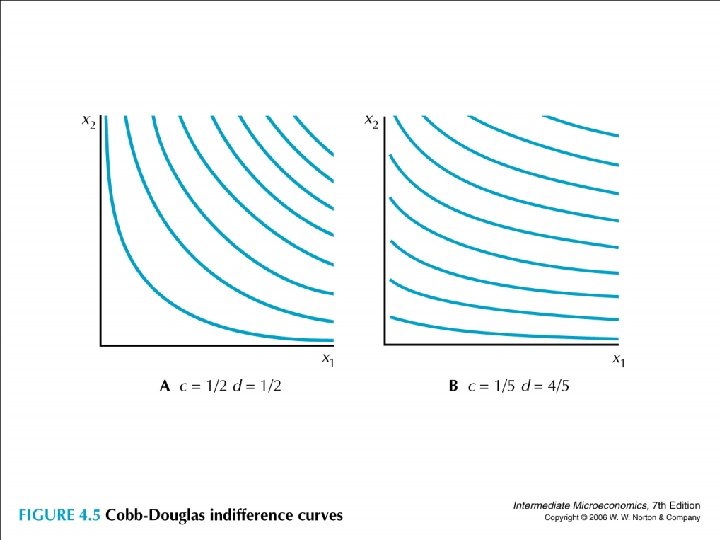
• Some examples of utility functions • Cobb Douglas, for instance • u(x 1, x 2) = x 1 x 2


• Generalizing, we might have • u(x 1, x 2) = x 1 cx 2 d • Interpret the exponents.


• Perfect substitutes such as • the 5 -dollar coin (x 1) vs. the 10 -dollar coin (x 2) • u(x 1, x 2) = 5 x 1 + 10 x 2

• u(x 1, x 2) = 5 x 1 + 10 x 2 • a units of x 1 can substitute perfectly for b units of x 2 • u(x 1, x 2) = x 1/a + x 2/b • u(x 1, x 2) = x 1/2 + x 2/1 • MRS 1, 2 = ∆x 2/ ∆x 1 = -b/a (intuitively correct)
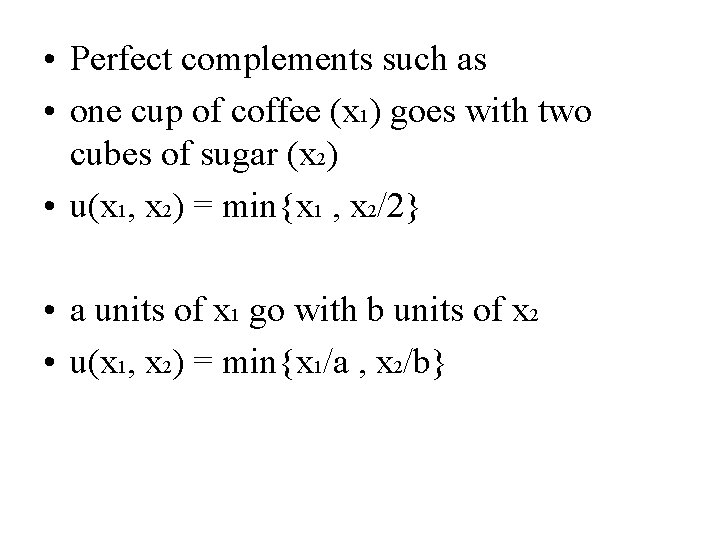
• Perfect complements such as • one cup of coffee (x 1) goes with two cubes of sugar (x 2) • u(x 1, x 2) = min{x 1 , x 2/2} • a units of x 1 go with b units of x 2 • u(x 1, x 2) = min{x 1/a , x 2/b}

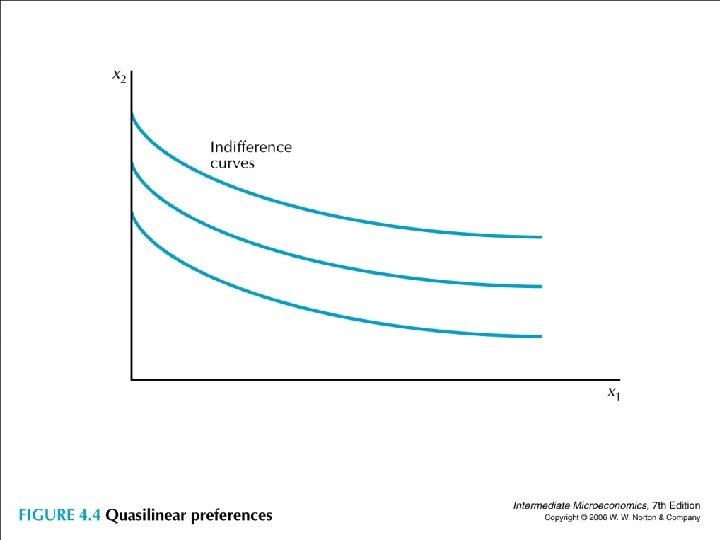
• • Quasilinear preferences (準線性) u(x 1, x 2) = v(x 1) + x 2 where v(∙) is concave or v’(∙)>0 and v’’(∙)<0 • v(x 1) = √x 1 • v(x 1) = ln(x 1)
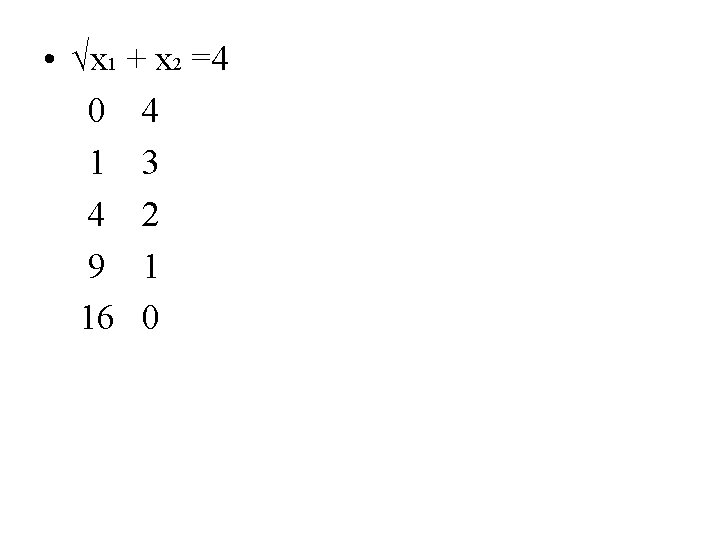
• √x 1 + x 2 =4 0 4 1 3 4 2 9 1 16 0


• The indifference curves are parrelle.

• Marginal utility • If we give the consumer a little more of good 1, how does his utility change?

• Marginal utility • the rate of the utility change with respect to the change of the consumption of one good • MU 1 = ∆u/ ∆x 1 = (u(x 1+ ∆x 1, x 2) - u(x 1, x 2))/ ∆x 1 • Specify where is it evaluated

• On an indifference curve: u(x 1, x 2) = k (a constant) MU 1 ∆x 1 + MU 2 ∆x 2 = 0 MRS 1, 2= ∆x 2/ ∆x 1= -MU 1 / MU 2

• Marginal utility depends on the utility function, but MRS does not. • MRS 1, 2= ∆x 2/ ∆x 1= -MU 1 / MU 2

• Marginal utility depends on the utility function, but MRS does not. • v(x 1, x 2) = f(u(x 1, x 2)) • MRS 1, 2 (v) = -MV 1 / MV 2 = -(∆ v/∆x 1)/ (∆v/∆x 2) = -[(∆ f/∆u)(∆u/ ∆x 1)]/ [(∆f/∆u)(∆u/ ∆x 2)] = -MU 1 / MU 2 = MRS 1, 2 (u)

• Additional materials • Lexicographic preferences: (x 1, x 2) w (y 1, y 2) if and only if (x 1 > y 1) or (x 1 = y 1 and x 2 ≥ y 2) • This is similar to the way the dictionary is ordered.

• Complete? Transitive? Monotonic? Indifference curves? Convex? Strictly convex? • Cannot be represented by any utility function

• Chapter 4 Utility • Key Concept: Utility, an indicator of a person’s overall well-being • We only use its ordinal property. • MRS does not depends on the utility function used. • MRS 1, 2= ∆x 2/ ∆x 1= -MU 1 / MU 2