Chapter 4 The Sequence Alignment Problem 1 The

Chapter 4 The Sequence Alignment Problem 1

The Longest Common Subsequence (LCS) Problem A string : S 1 = “TAGTCACG” n A subsequence of S 1 : deleting 0 or more symbols from S 1 (not necessarily consecutive). e. g. G, AGC, TATC, AGACG n Common subsequences of S 1 = “TAGTCACG” and S 2 = “AGACTGTC” : GG, AGC, AGACG n Longest common subsequence (LCS) : n S 1: TAGTCACG S 2: AGACTGTC LCS: AGACG n 2

Applications of LCS The edit distance of two strings or files. (# of deletions and insertions) S 1: TAGTCAC G S 2: AG ACTGTC Operation: DMMDDMMIMII n Spoken word recognition n Similarity of two biological sequences (DNA or protein) n n Sequence alignment 3

The LCS Algorithm n S 1 = a 1 a 2 am and S 2 = b 1 b 2 bn Ai, j denotes the length of the longest common subsequence of a 1 a 2 ai and b 1 b 2 bj. Dynamic programming: Ai, j = Ai-1, j-1 + 1 if ai= bj max{ Ai-1, j, Ai, j-1 } if ai bj A 0, 0 = A 0, j = Ai, 0 = 0 for 1 i m, 1 j n. n Time complexity: O(mn) n n 4
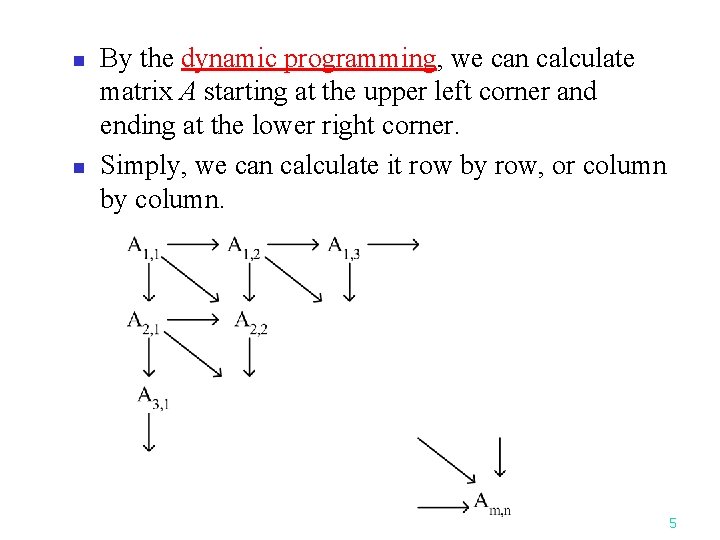
n n By the dynamic programming, we can calculate matrix A starting at the upper left corner and ending at the lower right corner. Simply, we can calculate it row by row, or column by column. 5

S 2 S 1 TAGTCACG AGACTGTC LCS: AGACG n After matrix A has been found, we can trace back to find the LCS. 6

Edit Distance(1) n To find a smallest edit process between two strings. S 1: TAGTCAC G S 2: AG ACTGTC Operation: DMMDDMMIMII 7

S 1 S 2 Edit Distance(2) TAGTCAC G AG ACTGTC DMMDDMMIMII 8

The Longest Increasing Subsequence (LIS) Problem n Definition: n n n Input: One numeric sequence S Output: The longest increasing subsequence in S Example: Given S = 35274816, the LIS in S is 3578. By applying the LCS algorithm, this problem can be solved in O(n 2) time. (Why? ) Robinson-Schensted-Knuth Algorithm can solve the LIS problem in O(nlogn) time. (See the example on the next page. ) 9

Robinson-Schensted-Knuth Algorithm for LIS Input 1 2 3 4 L n n 3 3 5 2 2 5 7 4 2 4 7 8 1 1 4 7 8 6 1 4 6 8 LIS: 3578 time complexity: O(nlogn) n n numbers are inserted and each insertion takes O(logn) time for binary search. 10

Hunt-Szymanski LCS Algorithm n n By extending the idea in RSK algorithm, the LCS problem can be solved in O(rlogn) time, where r denotes the number of matches. This algorithm is faster than traditional dynamic programming if r is small. 11
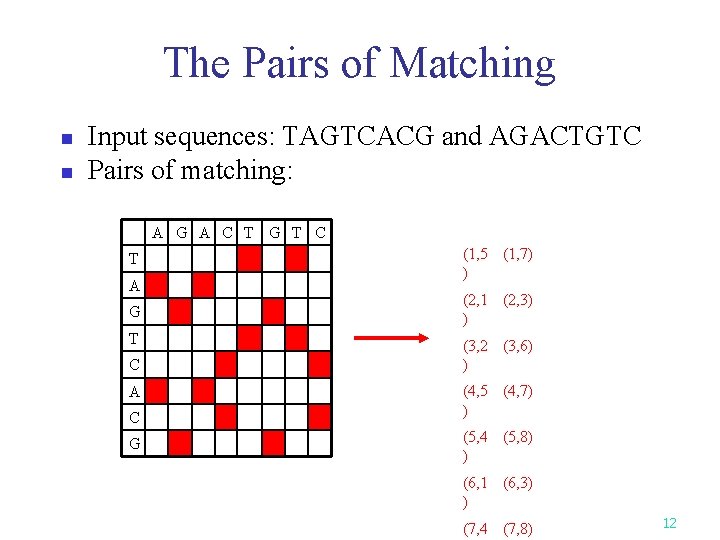
The Pairs of Matching n n Input sequences: TAGTCACG and AGACTGTC Pairs of matching: A G A C T G T C T A G T C A C G (1, 5 (1, 7) ) (2, 1 (2, 3) ) (3, 2 (3, 6) ) (4, 5 (4, 7) ) (5, 4 (5, 8) ) (6, 1 (6, 3) ) (7, 4 (7, 8) 12

Example for Hunt-Szymanski Algorithm n The insertion order is row major and column backward. (1, 7 (1, 5 (2, 3 (2, 1 (3, 6 (3, 2 (4, 7 (4, 5 (5, 8 (5, 4 ) ) ) ) ) L 1 (1, 7 (1, 5 (2, 3 (2, 1 (2, 1 ) ) ) ) ) 2 n n (3, 6 (3, 2 (3, 2 ) ) ) 3 Exercise: Please fill out the rest parts (4, 7 (4, 5 (5, 4 by yourself. ) matches ) ) ) Time Complexity: O(rlogn), r: # of 4 Each match needs O(logn) time for binary(5, 8 search. 13

The Longest Common Increasing Subsequence (LCIS) Problem n Definition: n n Input: Two numeric sequences S 1, S 2 Output: The longest common increasing subsequence of S 1 and S 2. Example: Given S 1=35274816 and S 2=51724863, the LCIS of S 1 and S 2 is 246 This problem can be solved by applying the RSK algorithm on the table for finding LCS(Chao’s Algorithm). (See the example on the next page. ) 14
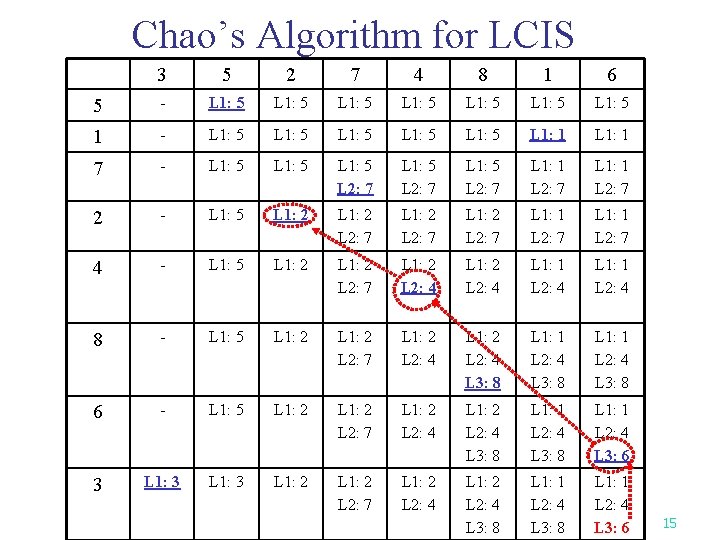
Chao’s Algorithm for LCIS 3 5 2 7 4 8 1 6 5 - L 1: 5 L 1: 5 1 - L 1: 5 L 1: 5 L 1: 1 7 - L 1: 5 L 2: 7 L 1: 5 L 2: 7 L 1: 1 L 2: 7 2 - L 1: 5 L 1: 2 L 2: 7 L 1: 1 L 2: 7 4 - L 1: 5 L 1: 2 L 2: 7 L 1: 2 L 2: 4 L 1: 1 L 2: 4 8 - L 1: 5 L 1: 2 L 2: 7 L 1: 2 L 2: 4 L 3: 8 L 1: 1 L 2: 4 L 3: 8 6 - L 1: 5 L 1: 2 L 2: 7 L 1: 2 L 2: 4 L 3: 8 L 1: 1 L 2: 4 L 3: 6 3 L 1: 2 L 2: 7 L 1: 2 L 2: 4 L 3: 8 L 1: 1 L 2: 4 L 3: 6 15

Analysis for Chao’s Algorithm n n n There are two types of operations to update the best tails, insert (match) and merge (mismatch). Direct implementation will take O(n 3) time, since it cost O(n) for each operation. However, it can be shown that each merge can be done in constant time. Also, all insertions in a row will totally take O(n) time. Thus, This is an O(n 2) algorithm 16

The Constrained Longest Common Subsequence (CLCS) Problem n Definition: n n Input: Two sequences S 1, S 2, and a constrained sequence C. Output: The longest common subsequence of S 1, S 2 that contains C. Example: Given S 1= TAGTCACG, S 2= AGACTGTC and C=AT, the CLCS between S 1 and S 2 would be AGTG. (LCS is AGACG) Purpose: n From biological perspective, we can specify the functional sites in input sequences by setting proper constraints. 17

The CLCS Algorithm n n n S 1 = a 1 a 2 am , S 2 = b 1 b 2 bn and C = c 1 c 2 cr Rk, i, j denotes the length of the longest common subsequence of a 1 a 2 ai , b 1 b 2 bj. and c 1 c 2 ck Dynamic programming: Rk, i, j = Rk-1, i-1, j-1 + 1 if ck = ai= bj Rk, i-1, j-1 + 1 if ck ai= bj max {Rk, i-1, j, Rk, i, j-1} if ai bj Rk, 0, 0 = Rk, i, 0 = Rk, 0, i = -∞ for 1 k r, 1 i m, 1 j n. R 0, i, j = Ai, j (LCS without constraint, please read previous pages) n Time complexity: O(rnm) 18

Example for CLCS Algorithm Input: S 1 = TAGTCACG, S 2 = AGACTGTC and C = AT CLCS of S 1 and S 2 with constraint C: (X means -∞) n n k=0 k = 1 (constraint A) - A G A C T G T C - - 0 0 0 0 0 - T 0 0 0 1 1 1 A 0 1 1 1 G 0 1 2 2 T 0 1 2 2 2 C 0 1 2 2 A 0 1 2 C 0 1 G 0 1 k = 2 (constraint T) A G A C T G T C - A G A C T G T C X X X X X - X X X X X 1 T X X X X X 1 1 A X 1 1 1 1 A X X X X X 2 2 2 G X 1 2 2 2 2 G X X X X X 3 3 T X 1 2 2 2 3 3 T X X X 3 3 3 3 4 C X 1 2 2 3 3 4 C X X X 3 3 3 4 A X 1 2 3 3 3 4 A X X X 3 3 3 4 2 3 4 4 4 C X 1 2 3 4 4 4 C X X X 3 3 3 4 2 3 4 4 5 5 5 G X 1 2 3 4 4 5 5 5 G X X X 3 4 4 4 Following the link, we can obtain the CLCS AGTG 19

Sequence Alignment S 1 = TAGTCACG S 2 = AGACTGTC ----TAGTCACG AGACT-GTC--n n TAGTCAC-G--ACTGTC Which one is better? We can set different gap penalties as parameters for different purposes. 20

Sequence Alignment Problem n Definition: n n n Input: Two (or more) sequences S 1, S 2, …, Sn, and a scoring function f. Output: The alignment of S 1, S 2, …, Sn, which has the optimal score. Purpose: n n To determine how close two species are To perform data compression To determine the common area of some sequences To construct evolutionary trees 21

Gap Penalty is the gap penalty. n n Suppose 22

Example for Sequence Alignment TAGTCAC-G--ACTGTC 23

PAM 250 Score Matrix 24

Blosum 62 Score Matrix 25

The Local Alignment Problem n n Input: Two (or more) sequences S 1, S 2, …, Sn, and a scoring function f. Output: Substrings Si’of Si such that the score obtained by aligning Si’ is the highest, among all possible substrings of Si. (1 i n) S 1= abbbcc S 1’= cc S 2= adddcc S 2’= cc Score=3 2+3 (– 1)=3 Score=2 2=4 26

Dynamic Programming for Local Alignment n Once the score becomes negative, we reset it to 0. 27

Example for Local Alignment - A G A C T G T C - 0 0 0 0 0 T 0 0 0 2 1 A 0 2 1 1 1 G 0 1 4 3 2 1 T 0 0 3 3 2 4 3 5 4 C 0 0 2 2 5 4 3 4 7 A 0 2 1 4 4 4 3 3 6 C 0 1 1 3 6 5 4 3 5 G 0 0 3 2 5 5 7 6 5 Two solutions: TAGTC T-GTC AGTCAC-G AG--ACTG 28

The Affine Gap Penalty n n n S 1=ACTTGATCC S 2=AGTTAGTAGTCC An optimal alignment: S 1=ACTT-G-A-TCC S 2=AGTTAGTAGTCC Original score=12 The following alignment may be better because there is only one gap. S 1=ACTT---GATCC S 2=AGTTAGTAGTCC Original score=6 29

Definition of Affine Gap Penalty n n A gap is caused by a mutational event which removes a sequence of residues. . A long gap is often more preferable than several gaps. An affine gap penalty is defined as Pg+k. Pe for a gap with k, k 1, spaces where Pg, Pe 0. Pg is related to the initiation of a gap and Pe is related to the length of the gap. 30

n n n Suppose that Pg=4 and Pe=1. S 1=ACTTGATCC S 2=AGTTAGTAGTCC S 1=ACTT-G-A-TCC S 2 =AGTTAGTAGTCC n Score=8 2 – 1 1 – 3 (4+1 1)=0 S 1=ACTT---GATCC S 2=AGTTAGTAGTCC Score=6 2 – 3 1 – (4+3 1)=2 31

Algorithm for Affine Gap Penalty n n A(i, j) is for the optimal alignment of a 1 a 2 ai and b 1 b 2 bj. A 1(i, j) is for that ai is aligned bj. A 2(i, j) is for that ai is aligned -. A 3(i, j) is for that - is aligned bj. 32

Multiple Sequence Alignment (MSA) n n n Suppose three sequence are involved: S 1 = ATTCGAT S 2 = TTGAG S 3 = ATGCT A very good alignment: S 1 = ATTCGAT S 2 = -TT-GAG S 3 = AT--GCT In fact, the above alignment between every pair of sequences is also good. 33

Complexity of MSA n 2 -sequence alignment problem: n Time complexity: O(n 2) 3 -sequence alignment problem: n n n (x, y, z) has to be defined. n Time complexity: O(n 3) k-sequence alignment problem: O(nk) 34

The Star Algorithm for MSA n n Proposed by Gusfield An approximation algorithm for the sum of pairs multiple sequence alignment problem Let (x, y)=0 if x=y and (x, y)=1 if x y. S 1 = GCCAT S 2 = G--AT S 2 = GA--T distance=2 distance=3 The distance induced by the alignment is define as 35

Distance n Properties of d(Si, Sj): n d(Si, Si) = 0 n Triangular inequality d(Si, Sj)+d(Si, Sk) d(Sj, Sk) n n i k j Given two sequences Si and Sj, the minimum distance is denoted as D(Si, Sj) d(Si, Sj) 36

Example for the Star Algorithm n S 1 = ATGCTC S 2 = AGAGC S 3 = TTCTG S 4 = ATTGCATGC n Try to align every pair of sequences: S 1= ATGCTC S 2= A-GAGC S 1= ATGCTC S 3= TT-CTG D(S 1, S 2) = 3 D(S 1, S 3) = 3 37

S 1= AT-GC-T-C S 2= AGAGC S 4= ATTGCATGC S 3= TTCTG D(S 1, S 4) = 3 D(S 2, S 3) = 5 S 2= A--G-A-GC S 3= -TT-C-TG- S 4= ATTGCATGC D(S 2, S 4) = 4 D(S 3, S 4) = 4 38

D(S 1, S 2)+D(S 1, S 3)+D(S 1, S 4) = 9 D(S 2, S 1)+D(S 2, S 3)+D(S 2, S 4) = 12 D(S 3, S 1)+D(S 3, S 2)+D(S 3, S 4) = 12 D(S 4, S 1)+D(S 4, S 2)+D(S 4, S 3) = 11 n S 1 is selected as the center since S 1 is the most similar to others. n Given a set S of k sequences, the center of this set of sequences is the sequence which minimizes n 39

n n n S 1 has been selected as the center. Align S 2 with S 1: S 1 = ATGCTC S 2 = A-GAGC Adding S 3 by aligning S 3 with S 1: S 1 = ATGCTC S 2 = A-GAGC S 3 = -TTCTG Adding S 4 by aligning S 4 with S 1: S 1 = AT-GC-T-C S 2 = A--GA-G-C S 3 = -T-TC-T-G S = ATTGCATGC 40

Approximation Rate n App 2 Opt (See the proof on the lecture note. ) 41

The MST Preservation for MSA n n n n In Gusfield’s star algorithm, the alignments between the center and all other sequences are optimal. Thus, (k– 1) distances are preserved. MST preservation is to preserves the distances on the edges in the minimal spanning tree. D: distance matrix based upon optimal alignments between every pair of input sequences. Dm: distance matrix based upon a multiple sequence alignment MST(D): MST based on D MST(Dm): MST based on Dm Goal: MST(D)=MST(Dm) 42

Example for MST Preservation Input: S 1 = ATGCTC S 2 = ATGAGC S 3 = TTCTG S 4 = ATTGCATGC n Step 1: Finds the pair wise distances optimally by the dynamic programming algorithm. S 1= ATGCTC S 1 = ATGCTC S 3= TT-CTG S 2 = ATGAGC D(S 1, S 2) = 2 D(S 1, S 3) = 3 n 43
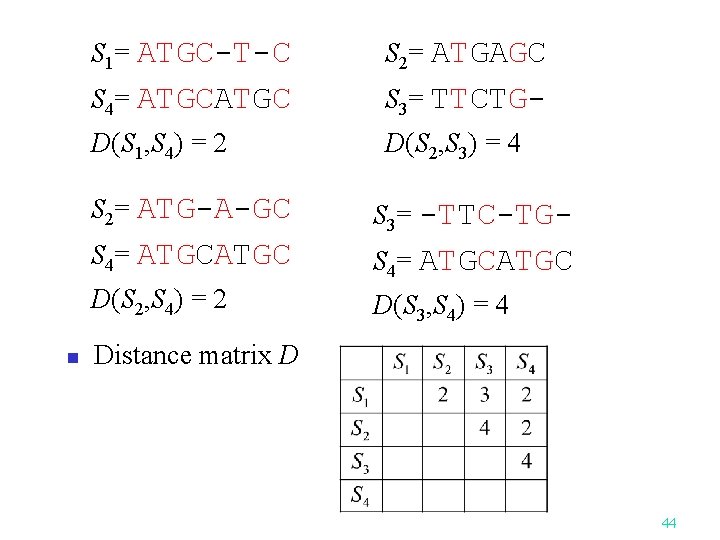
n S 1= ATGC-T-C S 2= ATGAGC S 4= ATGC S 3= TTCTG- D(S 1, S 4) = 2 D(S 2, S 3) = 4 S 2= ATG-A-GC S 3= -TTC-TG- S 4= ATGCATGC D(S 2, S 4) = 2 D(S 3, S 4) = 4 Distance matrix D 44
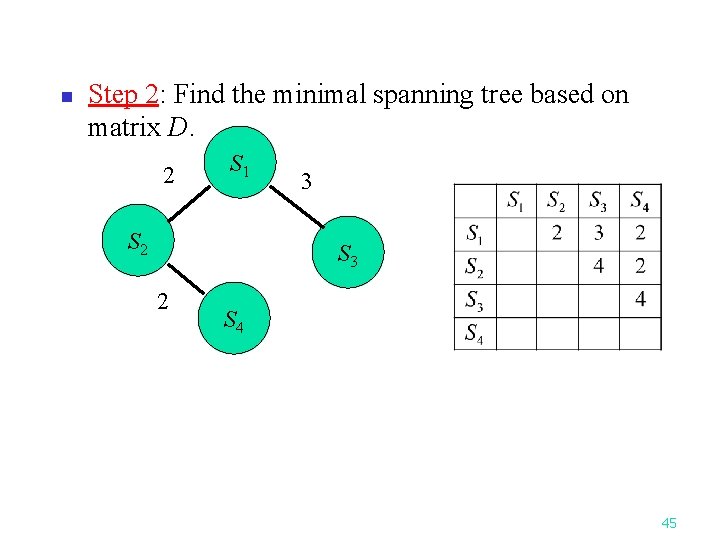
n Step 2: Find the minimal spanning tree based on matrix D. 2 S 1 S 2 3 S 3 2 S 4 45
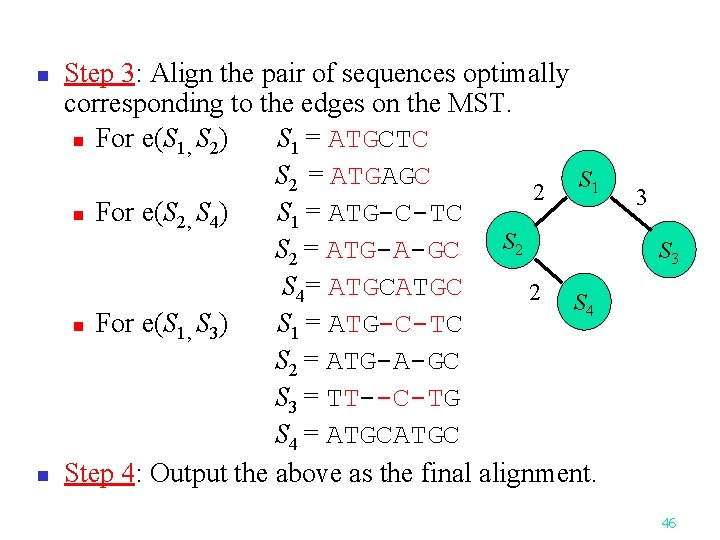
n n Step 3: Align the pair of sequences optimally corresponding to the edges on the MST. n For e(S 1, S 2) S 1 = ATGCTC S 2 = ATGAGC S 1 2 n For e(S 2, S 4) S 1 = ATG-C-TC S 2 = ATG-A-GC S 4= ATGC 2 S 4 n For e(S 1, S 3) S 1 = ATG-C-TC S 2 = ATG-A-GC S 3 = TT--C-TG S 4 = ATGC Step 4: Output the above as the final alignment. 3 S 3 46
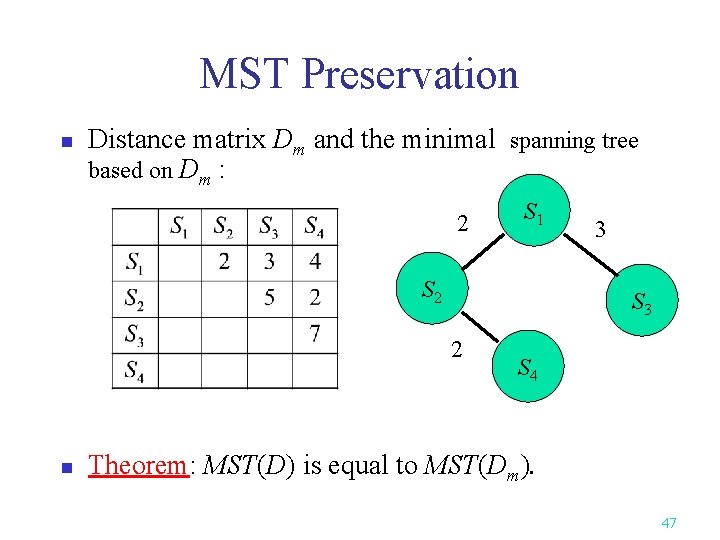
MST Preservation n Distance matrix Dm and the minimal spanning tree based on Dm : 2 S 1 S 2 S 3 2 n 3 S 4 Theorem: MST(D) is equal to MST(Dm). 47
- Slides: 47